Mathematica软件矢量分析功能及应用示例

林志立

(华侨大学 信息科学与工程学院， 福建 厦门 361021)

Mathematica软件矢量分析功能及应用示例

林志立

(华侨大学 信息科学与工程学院， 福建 厦门 361021)

本文介绍Mathematica软件在矢量分析方面的功能，包括坐标系设置与变换、矢量的表示与运算、标量场的梯度以及矢量场的散度、旋度等相关矢量计算函数，简要分析了Mathematica软件在标量场和矢量场图形展示方面的基本功能，并以多点电荷空间电位场和磁力矩器空间磁场的空间分布为例进行了代码编写和结果展示，以期应用于相关课程的计算机辅助教学，提高课堂教学效果和课程学习兴趣。

Mathematica软件；矢量分析；辅助教学

0 引言

矢量分析是以矢量为基本物理量的学科和课程的重要数学工具，一直是电磁学、光学理论类课程学习的重点和难点。矢量分析具有许多诸如求梯度、散度和旋度等复杂的数学计算，往往会使学生把精力放在公式推导和繁琐计算上，而忽视了内涵的物理图像、物理规律和物理思想方法，从而对其产生内容枯燥、抽象难学等抵触心理。此外，为更好地描述和理解矢量场的性质，绘制出矢量场随时空变化的三维图形十分必要，而手工绘制的只能是简单的示意图，不能得到直观精确的空间分布图景。这些缺点在不同程度上影响了矢量分析的教学效果，降低了学生的学习兴趣。

随着多媒体技术的推广，各种专业软件在课堂教学中的应用具备了硬件支撑条件，发挥越来越重要的作用。当前，以Matlab、Mathematica、Maple、MathCAD等为典型代表的专业数学软件已在许多科学计算、工程计算和数理化课程教学中获得大量的应用[1-3]。其中，Mathematica软件以其简洁友好的输入界面，出色的科学符号计算和图形展示功能，受到了很多教育和科学工作者的青睐[4-5]。将Mathematica软件应用到以矢量为基本物理量的课程教学中，用于课程计算机辅助教学，可以化解许多教学难点，使学生学习由难变易，使他们能把更多的精力放在分析物理问题、领会物理思想、培养科学思维方法等方面[6]。

本文主要介绍Mathematica数学软件所具备的诸如坐标设置与变换、标量场的梯度、矢量场的散度和旋度所对应的各种计算功能，分析Mathematica数学软件在标量和矢量图形展示方面的基本函数和相关指令，并结合两个例子来说明其功能和应用，以期帮助师生熟悉Mathematica软件所具备的矢量分析功能，提高课堂教学效果和课程学习兴趣。

1 Mathematica矢量分析功能

1.1 坐标系设置与转换

对于矢量场的求解，坐标系选择的好坏直接影响到问题求解的难易和表达式的简洁性。Mathematica支持包括笛卡尔坐标系、圆柱坐标系和球坐标系等在内的常用坐标系设置和转换，可满足各种形状结构的矢量场问题的求解需要。在Mathematica v9.0以上的各版本，使用CoordinateChartData函数进行坐标系设置。不同坐标系间的坐标变量关系可由CoordinateTransformData函数获取。空间某矢量的位置点在不同坐标系中的坐标转换可以通过CoordinateTransform函数实现，而标量场、矢量场、张量场在不同坐标系下的表达式转换则由TransformedField函数来完成，从而极大地简化了位置点和场量在不同坐标系间的转换。

1.2 矢量的表达与运算

矢量是既有大小也有方向的量。在三维正交坐标系中，矢量可以表示成三个坐标轴分量与相应的单位坐标矢量乘积的矢量之和。因此，三维矢量在Mathematica里可用以矢量的三个分量为元素的三元列表表示。例如，在直角坐标系下，矢量v=vxex+vyey+vzez可表示为v={vx，vy，vz}，其中vx，vy，vz分别代表了矢量v的x，y和z轴分量。二维的矢量v=vxex+vyey则可用含两个元素的列表v={vx,vy}即可表示。

在Mathematica中，对于给定的矢量v，可用Norm函数计算其模|v|；用Normalize函数生成矢量v对应的单位矢量v/|v|；用Part函数或[[ ]]符号提取v的某个坐标轴分量。

对于两个矢量v1和v2，可用Plus函数或“+”符号计算两矢量和；用Subtract或“-”符号计算两矢量差；用Dot函数或“.”符号计算两矢量的点积(标积)；用Cross函数或“×”符号计算两矢量的叉积(矢积)。另外，可用VectorAngle[v1,v2]计算两矢量间的夹角；用Projection[v1,v2]指令计算矢量v1在矢量v2上的投影；用EuclideanDistance[v1,v2]指令计算具有相同起点的两矢量的末端点距离。

1.3 标量场与矢量场的表达及运算

在Mathematica中，标量场可用以三个坐标轴变量为自变量的三元函数表示。例如：直角坐标系下的标量场u(x,y,z)=x2+2y+z3，利用Mathematica表达的指令为

u[x_,y_,z_]:=x^2+2*y+z^3

而三维矢量场可用含有三个元素的列表形式来描述，此时每个元素分别对应该矢量场的一个三元标量函数分量。例如，在直角坐标系中，

F[x_,y_,z_]:={Fx[x,y,z], Fy[x,y,z], Fz[x,y,z]}

即代表了矢量场F=Fxex+Fyey+Fzez，其中Fx，Fy和Fz分别是矢量场F的三个分量。

标量场和矢量场的常见矢量运算有：

(1)梯度。使用Grad[u,{x1, x2, x3},chart]指令可以计算标量场的梯度，其中函数Grad是梯度英文名gradient的缩略词。根据Mathematica对函数的命名规则，函数的首字母G应大写；u是标量场表达式；{x1, x2, x3}是坐标轴变量；chart是标量场表达式u所对应的坐标系类型。

(2)拉普拉斯运算。Laplacian函数是拉普拉斯运算的英文名Laplacian的全称，使用该函数可进行某标量或矢量场的拉普拉斯运算。例如使用Laplacian[u, {x1, x2, x3},chart]指令可求得某标量场u(x1,x2,x3)在坐标系chart下的拉普拉斯运算结果。

(3)散度。使用Div[{F1, F2, F3},{x1, x2, x3},chart]指令可以计算矢量场F={F1, F2, F3}的散度，其中函数Div是散度英文名divergence的缩略词；{F1, F2, F3}是矢量场的分量表达形式；{x1, x2, x3}是坐标轴变量；chart是矢量场表达式F所对应的坐标系类型。

(4)旋度。使用Curl[{F1, F2, F3},{x1, x2, x3},chart]指令可以计算矢量场F={F1，F2, F3}的旋度，其中Curl是旋度英文名curl的全称；{F1, F2, F3}是矢量场的分量表达形式；{x1, x2, x3}是坐标轴变量；chart是对应的坐标系类型。

1.4 矢量场图形可视化功能

Mathematica具有丰富的二维或三维矢量场图形可视化功能，可形象直观地展示矢量场的物理量大小和方向的空间分布特性。用于二维矢量场展示的函数主要包括矢量场的流线图StreamPlot函数、流线密度图StreamDensityPlot函数、矢量图VectorPlot函数、矢量密度图VectorDensityPlot函数等，可展示二维矢量场的流向、方向以及大小空间分布等特性。对于三维矢量场，可用于图形展示的函数主要包括三维矢量图VectorPlot3D函数、三维矢量切片图SliceVectorPlot3D函数等。在二维或三维矢量场场量大小的图形展示方面，有DensityPlot或DensityPlot3D函数可画出二维或三维空间密度图，利用ContourPlot或ContourPlot3D可画出二维或三维场空间轮廓图。对于离散数据场，只要在以上函数名称前面加上List也同样可以绘制出相应的图形，例如三维离散矢量场的展示应该用ListVectorPlot3D这个函数。同时，辅以Animate和Manipulate等动画命令，便可实现对电磁波等时变电磁场的空间动态演示。

2 Mathematica应用示例

2.1 多个点电荷空间电位场计算与展示

本示例利用Mathematica计算和展示多个点电荷在三维空间产生的电位场和电场分布。根据电磁理论，由N个点电荷产生的电位场为

(1)

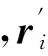
potential[qc_, rp_,r_]:= 1/(4*Pi*epsilon)*Sum[qc[[i]]/Norm[r-rp[[i]]],{i,Length[qc]}]

指令中电荷量qc应是以N个点电荷的电荷量为元素的一维列表，代表各电荷位置的矢量rp应是含N个三元位置列表{xi,yi,zi}的二重列表，场点位置矢量r应该是三元列表{x,y,z}。根据电场与电位的关系，静电场计算表达式为

E=-▽φ

(2)

上式涉及到梯度计算，可用Grad函数实现：

electricField[q_, rp_}] = -Grad[potential[q, rp,r], r] /. Abs′[x_] :> x/Sqrt[x^2]

由上面两个函数的定义表达式可见Mathematica软件强大的矢量计算功能，用简短的指令即可实现复杂的电位和电场的三维空间分布计算。同时，Mathematica还有强悍的图形可视化功能。以分别位于x1=1米和x2=-1米处的两个正负点电荷(q1=-2,q2=4πε库仑)的空间电位场展示为例，使用以下简单指令可描绘出电位场的三维等值面图，如图1所示。

ContourPlot3D[Evaluate[potential[{4*Pi*epsilon, -2*Pi*epsilon }, {{1, 0, 0}, {-1, 0, 0}}, {x, y, z}]], {x, -6, 6}, {y, 0, 6}, {z, -4, 4}, Contours -> {-1, -0.75, -0.25, -0.1, 0, 0.1, 0.25, 0.75, 1}, ContourStyle -> Table[Hue[i/7, 1, 1, 0.5], {i, 0, 6}], Mesh -> None, BoxRatios -> Automatic]

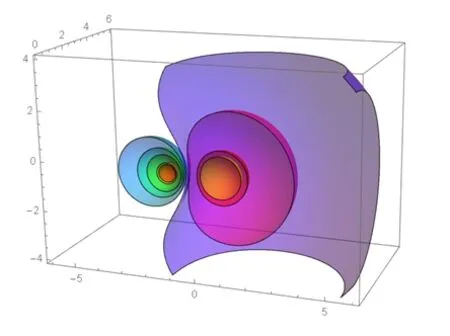
图1 正负点电荷的三维等电位面

2.2 磁力矩器的磁场计算与展示

磁力矩器在小卫星姿态控制中具有重要的作用，它由软磁体外绕线圈组成，当其直径远小于长度时，其激发的磁场可以看作很多个磁偶极子激发的磁场的矢量累加。假设磁力矩器的总剩磁矩为m，长度为L，沿磁力矩器主轴将其分成长度为dl的小段磁偶极子单元，对各单元的磁场进行积分，即可得磁力矩器在未加电流时在空间产生的磁场计算公式为

(3)

其中，rd为空间场点离开积分单元dl的距离矢量。式(3)中既有矢量矢量模rd=|rd|的计算，也有矢量点积的计算，以及复杂的积分，因此特别适合用Mathematica软件来计算磁力矩器在空间形成的磁场分布。具体计算代码如下：

L = 1;

m = {0, 0, 50};

rd = {x, y, z - l};

H = Table[1/(4*[Pi]*L)*NIntegrate[(3*rd*(m.rd))/Norm[rd]^5 - m/Norm[rd]^3, {l, -L/2, L/2}], {x, -0.25, 0.25, 0.07}, {y, -0.25, 0.25, 0.07}, {z, -0.25, 0.25, 0.07}];

ListVectorPlot3D[H, VectorPoints -> 5, VectorStyle -> {g}, VectorColorFunction -> Hue,

AxesLabel -> {x, y, z}]

指令中用H代表磁力矩器产生的磁场，使用ListVectorPlot3D函数来绘制三维磁场矢量图。运行以上指令，即可获得磁力矩器在空间产生的磁场的三维矢量分布如图2所示。

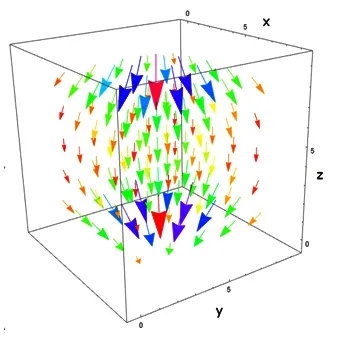
图2 磁力矩器产生的磁场矢量空间分布

3 结语

本文首先介绍了Mathematica软件在矢量分析方面所具备的强大计算功能，包括坐标系设置和变换、矢量的表示与相关运算、标量场的梯度以及矢量场的旋度、散度等相关运算。简要分析了Mathematica数学软件在标量场和矢量场图形展示方面的基本函数和指令。以多点电荷空间电位场和磁力矩器空间磁场的分布为应用范例，充分展示了Mathematica软件在矢量分析计算和图形展示领域具有指令简洁、功能强悍、图形可视化效果好等特点。本文所介绍的内容和成果可用于“电磁场与电磁波”、“物理光学”等以矢量为基本物理量的电磁理论类课程的辅助教学之用，可全面提升学生的复杂计算、公式推导和图形可视化演示能力，提高学生对相关课程的学习兴趣。

[1] 徐安农. Mathematica数学实验[M]. 北京: 电子工业出版社, 2004年7月

[2] 邵小桃, 郭勇, 李一玫.“电磁场与电磁波”课程的Matlab辅助教学[J]. 南京: 电气电子教学学报, 2010, 32(5): 111-113

[3] 欧攀, 林志立, 江洁. Matlab数值计算在光学仿真和教学中的应用[J].石家庄: 教育教学论坛, 2012, 38:80-81

[4] 杜建明. Mathematica在电磁场理论中的应用[M]. 合肥: 合肥工业大学出版社, 2004年12月

[5] 董键. Mathematica与大学物理计算[M].北京: 清华大学出版社, 2010年9月

[6] 于凤梅, 王克强, 张麟. 运用Mathematica软件辅助大学物理教学[J]. 北京: 中国现代教育装备, 2011, 15:29-31

Vector Analysis Functions and Application Examples of Mathematica Software

LIN Zhi-li

(CollegeofInformationScienceandEngineering,HuaqiaoUniversity,Xiamen361021,China)

In this paper the vector analysis functions of Mathematica software are described, including the coordinate system setting and transformation, the vector representation and operation, as well as the gradient of scalar field, the curl and divergence of vector field and so on. A brief analysis of Mathematica software in scalar field and vector field graphic displaying functions is also presented. Two examples including the potential field of charged particles and the magnetic field of magnetorquer are presented in order to help apply Mathematica to improve the teaching effect and learing interest that promote the computer-aided instruction of relevant courses.

Mathematica software; vector analysis; assisted teaching

2015-11-11;

2016-01-22 基金项目：2016年福建省本科高校教育教学改革研究项目资助(项目编号：JZ160081)

林志立(1980-)，男，博士，副教授，主要从事高等电磁理论、计算电磁学领域研究工作，E-mail：alizlzl@163.com

O441.4

A

1008-0686(2016)05-0143-04