基于Matlab的弱导光纤模式特性仿真

马愈昭， 许明妍， 范 懿， 张 喆

(中国民航大学 1. 民航气象技术研究所； 2. 电子信息工程学院， 天津 300300)

基于Matlab的弱导光纤模式特性仿真

马愈昭1，2， 许明妍2， 范 懿2， 张 喆2

(中国民航大学 1. 民航气象技术研究所； 2. 电子信息工程学院， 天津 300300)

本文介绍了在Matlab中实现弱导光纤本征方程的求解和模式特性的仿真，阐述了相应的仿真实验设计思想。基于Matlab的的弱导光纤模式特性仿真实验主要应用于“光纤通信”课程的实践教学中，相应的实验设计思想也可用于部分专业课程中传输线和波导的仿真实验中。

光纤通信；模式；本征方程

0 引言

“光纤通信”是我校通信工程专业(现代通信方向)本科生的一门重要专业课程[1,2]。在该课程讲授的内容中，光纤模式理论历来是教学的重点和难点。此部分内容涉及大量数学推导，例如，光纤中传导模式的本征方程及电磁场分布是通过麦克斯韦方程，经过复杂的推导过程才得到的。公式推导过程繁琐、结果抽象复杂。为此我们针对此部分内容设计了仿真实验[3-5]。在此之前，我们已在该课程仿真实验教学中引入了基于高级数值方法模拟仿真物理场问题的通用软件平台COMSOL Multiphysics，用于光纤模式特性的仿真[6,7]。而本文，我们介绍的是在通用数学软件Matlab中实现弱导光纤模式特性的仿真，同样是对光纤模式特性的仿真，在Matlab中仿真与在COMSOL中仿真对学生和教师的要求差别很大。在COMSOL中对光纤模式特性进行仿真，主要要求学生掌握基本光纤参数的设定及使用COMSOL对光纤问题进行仿真的一般流程。而在Matlab中对光纤模式特性进行仿真，对学生的编程能力和对光纤模式本征方程意义的理解，以及求解非线性方程的能力有较高要求。

本文着重阐述在Matlab中对弱导光纤模式特性进行仿真所依据的光纤模式理论基础、Matlab仿真程序以及仿真实验教学的几个要点。

1 弱导光纤模式理论

阶跃光纤是目前应用最广泛的光纤产品，其结构最为简单，由芯层、包层、涂覆层组成，如图1(a)所示。芯层和包层决定了光纤的光学特性，其芯层折射率比包层折射率大，折射率分布如图1(b)所示。

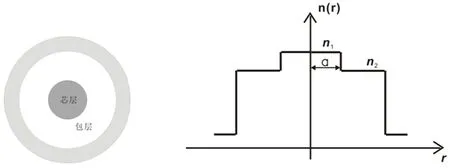
(a)横截面 (b)折射率分布 图1 阶跃光纤

通常的阶跃光纤芯层折射率n1与包层折射率n2相差很小，称为弱导光纤。根据光波导模式理论，弱导光纤中传导的LP模式的特性如图2所示[8]。

图2 弱导光纤LP模归一化传播常数

图2中给出了阶跃光纤较低的几个LP模式的归一化传播常数beff随归一化频率V值变化的规律。V定义如下：

V只与光纤的固有属性以及激励光纤的光波波长λ有关。a为光纤芯层半径，NA为光纤的数值孔径。图2纵坐标为归一化传播常数beff，它与模式传播常数密切相关

其中，neff=β/k为有效模式折射率，β为传播常数，k=2πλ为波数。使用电磁场与电磁波理论研究光纤模式特性有两种方法：一种是使用电磁场仿真专用工具，如COMSOL，此方法可以获得Maxwell方程的精确解，得到的是矢量模式，以TE、TM、HE、EH命名;第二种方法是使用Gloge提出的弱导近似理论，适用于弱导光纤，仅能获得Maxwell方程的近似解，获得的模式以LP命名[8-10]。Gloge给出了弱导条件下光纤本征方程的近似形式

(1)

式中

(2)

J为第一类贝塞尔函数，K为第二类修正贝塞尔函数。m-1和m为贝塞尔函数的阶数。根据本征方程(1)可解出模式传播常数β，进而根据已推出的解析式得出光纤各模式的电磁场分布，以及色散等模式传播特性，求解过程并不复杂，因此可以在Matlab中采用数值解法实现。这正是我们设计基于Matlab的弱导光纤模式特性仿真实验的理论依据。

2 弱导光纤模式特性仿真程序设计

在Matlab中实现弱导光纤模式特性仿真的程序流程如图3所示。

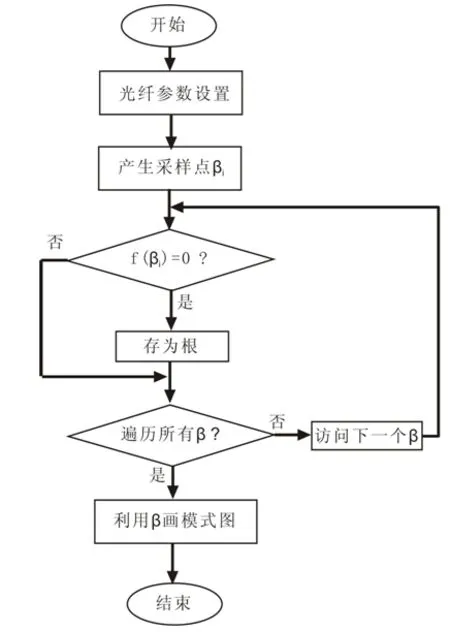
图3 光纤模式特性Matlab仿真流程

完成模式特性仿真的关键是用本征方程(1)解出模式传播常数β，由于学生首次独立编程实现非线性方程的求解，因此鼓励学生使用原理相对简单的穷举法，首先根据本征方程(1)构造函数f(β)

(3)

依据精度要求，将β的取值范围均分为N个区间，求出β的步长，得到采样点βi(i=1…N+1)。根据式(2)逐一计算对应Ui和Ki的值，并计算f(βi),判断是否满足f(βi)=0，满足f(βi)=0的β即为本征方程(1)的根，从而得出光纤各模式的电磁场分布。

在图3中，弱导光纤模式特性的Matlab仿真程序包含以下几个部分。

1)参数设置

主要包括光纤芯层折射率n1、包层折射率n2、芯层半径a以及光波波长λ的设置，以及求解本征方程时将β的取值范围划分的区间个数N。

2)确定自变量采样点βi

依据光纤模式理论，β的取值范围为n2k≤β≤n1k，将范围均匀分成N个区间，求出β的步长Δβ=(n1k-n2k)/N，得到β的采样点βi=n2k+(i+1)·Δβ(i=1…N+1)。

3)计算函数f(βi)值

根据式(2)、(3)计算每个β值对应的Ui和Ki的值，从而计算函数f(βi)的值。

4)找出本征方程的根

满足f(βi)的β值即是本征方程的根。在得到每个β值对应f(βi)后，计算相邻的函数值乘积f(βi)·f(βi+1)的值，若f(βi)·f(βi+1)<0，则β0=(βi+βi+1)/2被确定为本征方程的根。依据光纤模式理论，如果光纤中存在一个LP模，则能求得一个根β01，如果存在n个LP模，则能求得n个根，β01,β02……β0n。可以根据弱导近似理论预先由光纤的归一化频率V值和图2确定n值。

5)画模式图

利用求得的本征方程的根β0画出光纤各个LP模在光纤横截面上的二维光强分布图。

在某参数设置条件下利用所设计的Matlab程序仿真所得的弱导阶跃光纤几个LP模式的横向光强分布(按传播常数减小顺序)如图4所示。

图4 阶跃光纤LP模横向光强分布

3 实验教学设计

在基于Matlab的光纤模式特性仿真实验教学实践中强调以下几点：

1)物理概念

光纤模式特性问题实质是电磁场理论在光波导中的应用，在基于Matlab的光纤模式特性仿真中，学生必须掌握弱导光纤本征方程的推导过程，了解本征方程的物理意义。本征方程的推导需要结合电磁场与电磁波课程中Maxwell方程、波动方程、边界条件等知识点。在仿真之前，学生可预先依据图2确定特定V值条件下光纤理论上应传导的LP模式数量，深刻理解归一化频率V的物理意义。

2)数学算法

在本实验中，完成模式特性仿真的关键是用本征方程(1)解出模式传播常数β，式(1)是含有贝塞尔函数的非线性方程，不存在解析解，因此必须在Matlab中用数值解法求出β。数值解法求解非线性方程的方法有很多，本实验采用原理上比较简单的穷举法，在采用穷举法求出β后还可以鼓励学生对算法本身的速度、精度进行深入研究，例如，仿真中须设置的参数N决定了拟将β的取值范围划分的区间数，它直接影响仿真的速度和β的求解精度。此外，还可以启发学生使用其他原理复杂、计算精度高、收敛速度快的方法，如二分法、牛顿法，Jarratt迭代法等。

3)仿真工具比较

在本实验中，所得的光纤模式光学特性是基于求解弱导光纤本征方程解出的传播常数β，因此所设计的仿真程序只适用于弱导条件下的标量模，即LP模。而采用COMSOL，获得的是Maxwell方程的精确解，获得光纤中的所有矢量模式。可鼓励有精力的学生对矢量模式和LP模进行比较，同时对两种仿真方法的理论依据、算法特性、应用范围进行对比分析。也可将所设计的Matlab仿真程序进行扩展，由求解近似的本征方程扩展为求解原始形式(精确)的本征方程，探讨在Matlab中实现光纤矢量模式特性仿真的实验设计。

4)参数化研究

学生完成仿真程序设计后，还可以改变光纤的芯层半径、芯层折射率、包层折射率以及光波波长，考察这些参数对光纤传导的模式数量、模式光强分布以及传播常数或色散等传播特性的影响。实现光纤模式光学特性的参数化研究。其研究的原则是，保持其它参数不变，研究光纤模式光学特性随某一特定的参数的变化规律。

(马愈昭等文)

5)特殊问题的解决

在仿真程序设计过程中还存在其他一些问题，上面的讨论并没涉及，比如由于本征方程(1)的分母Jm(U)可能出现零值，导致方程无意义，因此经程序判断所得的传播常数β的根，如果导致Jm(U)=0，就必须剔除，可以启发学生独立思考，加入相应的判断程序剔除无意义的β解。此外，在绘制光纤模式光强分布时，必须注意，对于同一传导模式，光纤的芯层和包层模式电场强度分布是由不同的解析式给出的，所以对于每一模式必须分别绘制芯层和包层光强分布，然后拼接在一起。

4 结语

本文在Matlab中实现弱导光纤模式光学特性的仿真，展示了利用该仿真程序对特定结构光纤进行仿真的部分结果，并介绍了基于Matlab光纤模式特性进行仿真实验教学须重视的几个要点。作为实验实施的前期准备工作，我们在实验实施前将仿真中涉及的本征方程推导、边界条件应用、贝塞尔函数特性、非线性方程的数值解法等内容作为课外作业分四次布置给学生，仿真实验实施要求学生在2学时内设计出完整的仿真程序，并进行讲解、答疑、讨论。整体的思维训练过程遵循由简单到复杂、由理论到实践、由演示到设计的过程。将基于Matlab的光纤模式特性仿真实验引入到我校“光纤通信”课程的教学活动中，使学生们对光纤模式理论有更深的认识，有效地激发了学生学习“光纤通信”课程的积极性，也培养了学生独立、严谨的研究性思维。

[1] 刘增基. 光纤通信[M]. 西安：西安电子工业大学出版社，2001.

[2] 原荣. 光纤通信[M]. 北京：电子工业出版社，2006。

[3] 徐文云. 实验与仿真在光纤通信教学改革中的应用研究[J]. 重庆:重庆邮电大学学报(社会科学版)，2007， 增刊：183-186.

[4] 周雪芳，王天枢. 仿真软件在《光纤通信》实验教学中的应用研究[J]. 成都:实验科学与技术，2011，第 9卷(5)：53-56.

[5] 王秀琳，张爱玲. 多层次教学在高职光纤通信中的应用[J]. 济南:科技信息，2013，(2)：278.

[6] Step-Index Fiber(Solved with COMSOL Multiphysics 4.2a)[EB/OL]. USA：COMSOL Inc.，2011.

[7] 马愈昭，许明妍，范懿，张喆，吴仁彪. 基于COMSOL 4.2的波导模式特性仿真[J]. 南京:电气电子教学学报，2015，第 37卷(1)：114-117.

[8] D. Gloge, Weakly guiding fibers[J], Washington, Appl. Opt, 1971, vol. 10: 2252-2258.

[9] A.W. Snyder and J. D. Love. Optical Waveguide Theory[M]. London：Chapman and Hall, 1983.

[10] A. Yariv. Optical Electronics in Modern Communications[M], 5th edition, UK：Oxford University Press, 1997.

Simulating Modes Properties of Weakly-Guiding Fibers Using Matlab

MA Yu-zhao1,2, XU Ming-yan2, FAN Yi2, ZHANG Zhe2

( 1.InstituteofCivilAviationMeteorologicalTechnology, 2．CollegeofElectronicInformationEngineeringCivilAviationUniversityofChina,Tianjin300300,China)

In the paper, we have solved the eigen-value equation of the weakly-guiding fibers and further investigated the optical properties of fiber modes in the Matlab. Several attentions should be paid in the design of the simulation program. Our work is useful for improving the lecture of the Optical Fiber Communications course. The ideas can also be used in simulating the modes properties of other waveguides and the signal properties of transmission line in the relevant lectures of universities.

optical fiber communications; modes; eigen-value equation

2015-11-12;

2015-12-23基金项目：中国民航大学 教育教学改革研究课题(205002240253) 国家自然科学基金(U1533113) 中央高校基本科研业务费 中国民航大学专项(3122016B001)

马愈昭(1978-)，女，博士，讲师，主要从事通信工程领域教学与研究工作，E-mail: yzma@cauc.edu.cn

G642, TN252

A

1008-0686(2016)05-0127-04