文氏桥振荡器的簇发现象分析及实验验证

徐 权， 张琴玲， 史国栋

(常州大学 信息科学与工程学院, 江苏 常州 213164)

文氏桥振荡器的簇发现象分析及实验验证

徐 权， 张琴玲， 史国栋

(常州大学 信息科学与工程学院, 江苏 常州 213164)

本文采用一对二极管将无源LC滤波器非线性耦合到文氏桥振荡器的并联桥臂替换电阻，实现了一种新颖的文氏桥振荡器；建立了该电路的动力学模型，开展了动力学行为分析。结果表明：文氏桥振荡器在给定的参数域内具有快慢效应。进一步研究了混沌簇发和周期簇发现象。本文研制了实验电路，该实验电路结构简单、易物理实现，实验测量和数值仿真两者结果一致，证明了理论分析的有效性。

周期簇发振荡; 混沌簇发振荡；文氏桥振荡器

0 引言

簇发振荡现象存在于具有真实时间的快慢效应或几何尺寸上的尺度效应的系统中，由于慢标子系统对快标子系统行为的不断调节，系统在平衡点或静息态与激发态之间相互转迁而产生簇发振荡。根据系统分岔行为，可将簇发振荡分为fold/fold簇发、fold/Hopf簇发、Hopf/Hopf簇发等。在诸如耦合混沌系统、蔡氏振荡电路、文氏桥振荡电路、周期激励混沌电路、开关变换器等系统中，系统表现为混合模态振荡即簇发振荡[1～5]。

目前对蔡氏电路及改进型蔡氏电路中簇发振荡及分岔机理分析研究较多，而对文氏桥振荡器中的簇发现象及分岔机理研究相对较少[2-4]。文献[3]将忆阻引入传统文氏桥振荡器，分析了簇发振荡现象的分岔机理。

本文采用一对二极管将无源LC滤波器非线性耦合到文氏桥振荡器RC并联支路以替换电阻，从而构成一种新颖的文氏桥振荡器。该振荡器有着电路结构简单、物理实现容易、电路特性稳定等优点。

1 四阶文氏桥振荡器

新提出的文氏桥振荡器电路如图1所示，它含有四个动态元件电容C1、电容C2、电容C3和电感L，分别对应四个状态变量为v1、v2、v3和iL。考虑到运算放大器的“虚短路”和“虚断路”特征，并根据基尔霍夫电压、电流定律和元件本构关系，可得描述电路的微分方程组为

(1)

其中k=Rf/Ri，ρ=1/(nVT)，IS，n和VT分别为二极管的反向饱和电流、发射系数和温度电压。

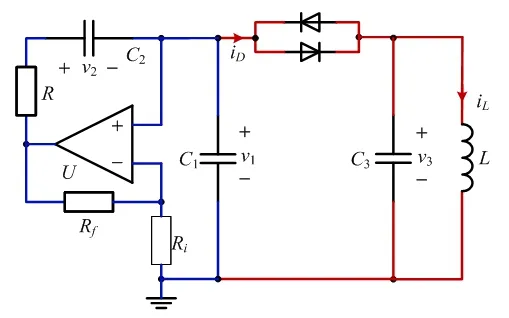
图1 四阶文氏桥振荡器

电路中二极管采用1N4148型，相应参数为IS= 6.8913 nA，n=1.8268和VT= 25 mV，典型电路参数为C1=1 nF，C2= 10 nF，C3=4.7 nF，L= 10 mH，Ri=2 kΩ，Rf= 6 kΩ。

2 依赖于电路参数R的动力学行为

选取典型电路参数，并以R为变量，电路状态变量v1(t)的分岔图如图2(a)所示，由Wolf算法计算得到的李雅普诺夫指数谱如图2(b)所示，电路状态变量初值为v1(0) =0 V、v2(0)=0.01 V、v3(0)=0 V和iL(0) =0 A。在图2(b)中，为清晰起见，只给出了最大的3根李雅普诺夫指数LE1、LE2和LE3。此外，图2(a)中分岔图和图2(b)中李雅普诺夫指数谱在各参数区间所呈现的动力学行为是完全一致的。

当R增大时，可相应地将文氏桥振荡器状态变量v1(t)的分岔图和李雅普诺夫指数谱划分为两个参数区间分析，分别为R∈[20 kΩ, 27.6 kΩ]和R∈(27.6 kΩ, 35 kΩ]。当R在[20 kΩ, 27.6 kΩ]区间逐渐变大时，文氏桥振荡器的动力学行为从周期轨道 (LE1= 0且LE2< 0) 进入混沌轨道(LE1> 0且LE2= 0)，后经逆倍周期分岔进入周期轨道(LE1= 0且LE2< 0)。当R在(27.6 kΩ, 35 kΩ]区间内逐渐增大时，文氏桥振荡器的动力学行为从混沌轨道(LE1>0且LE2= 0)，最终运行轨线落入准周期轨道(LE1=0且LE2<0)。另外，在混沌区域内存在周期窗，对应最大李雅普诺夫指数等于零。

图3给出电路参数R取不同值时，文氏桥振荡电路在v1(t)-v3(t)平面上的相轨图, 当R分别为22 kΩ和24.5 kΩ时，相轨图分别如图3(a)和3(b)所示，分别为混沌轨道和周期轨道。特别地，图3(c)和3(d)分别为混沌簇发振荡和周期簇发振荡。下面对簇发振荡现象进行详细地分析。

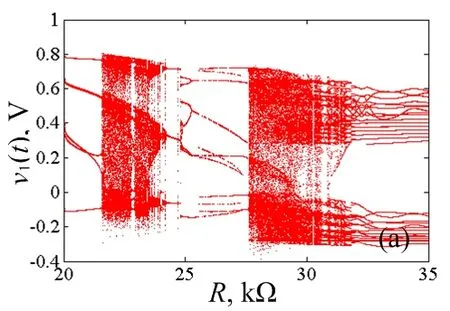
(a) 状态变量v1(t)的分岔图

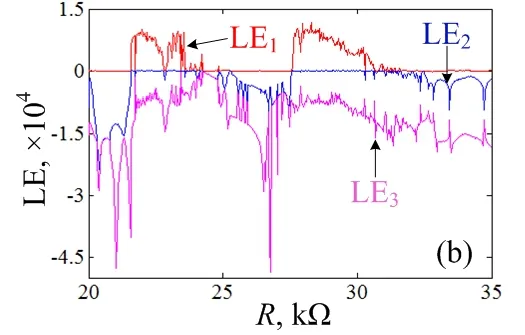
(b) 李雅普诺夫指数谱图2 文氏桥振荡电路的动力学行为

3 簇发振荡的数值仿真

由图3(c)和(d)可知，文氏桥振荡电路存在两种对称的簇发振荡，分别为混沌簇发振荡和周期簇发振荡。

为了更清晰、详实地演绎文氏桥振荡电路簇发振荡现象的产生机理，相应于图3(c)和(d)，图4和图5分别给出了v2(t)-v1(t)平面上的相轨图及v1(t)和v2(t)的时域波形。

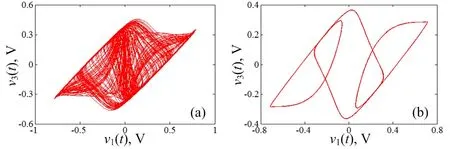
(a) R = 22 kΩ (b) R = 24.5 kΩ

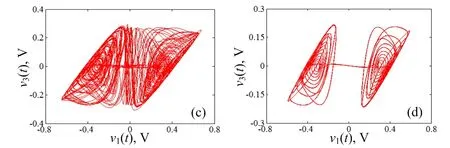
(c) R = 30 kΩ (d) R = 34 kΩ图3 电路参数R对应v1(t)-v3(t)平面上的相轨图

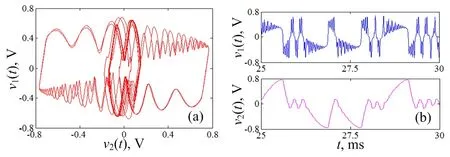
(a) v2(t)-v1(t)平面上的相轨图 (b) v1(t)与v2(t)的时域波形图4 混沌簇发振荡(R= 30 kΩ)

(a) v2(t)-v1(t)平面上的相轨图 (b) v1(t)与v2(t)的时域波形图5 周期簇发振荡(R= 34 kΩ)

4 实验验证

按照图1所示的电路原理图，容易制作出相应的实验电路。这里，分立元件包括：精密可调电阻、独石电容、手工绕制电感和1N4148二极管，实验采用典型电路参数并采用Tektronix TDS 3034C数字存储示波器捕获测量结果。

改变精密电阻R的值，可得不同R值对应的文氏桥振荡器在v1(t)-v3(t)平面上的相轨图如图6所示。为进一步地验证簇发振荡现象，图7和图8所示为从示波器分别获取的R=30 kΩ和R= 34 kΩ文氏桥振荡器在v2(t)-v1(t)平面上的相轨图及时域波形。

对比相应的实验测量与数值仿真结果发现，实验测量与数值仿真有着较好的一致性，由此印证了文氏桥振荡系统的簇发振荡行为。

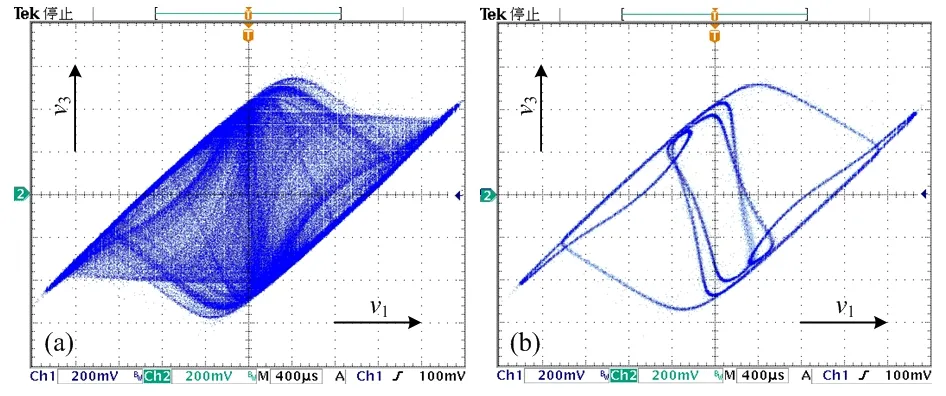
(a) R = 22 kΩ (b) R = 24.5 kΩ

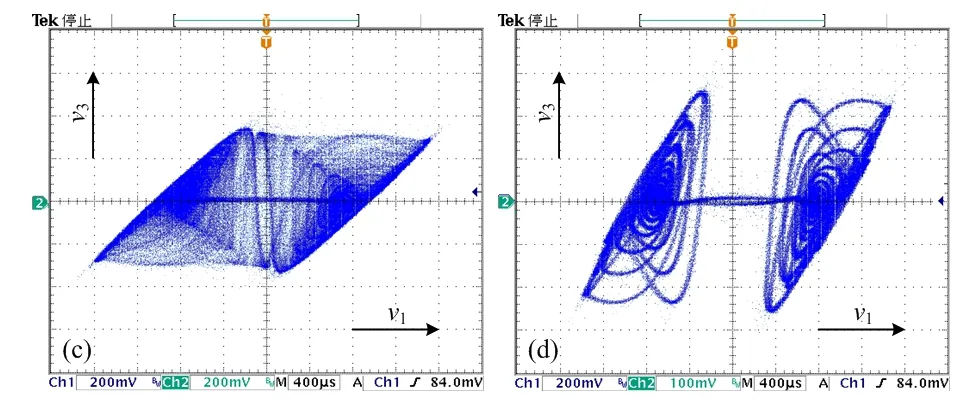
(c) R = 30 kΩ (d) R = 34 kΩ 图6 不同电阻值R时，实验测得v1(t)-v3(t)平面内相轨图

(a) v2(t)-v1(t)平面上的相轨图 (b) v1(t)与v2(t)时域波形图7 实验测量混沌簇发振荡(R = 30 kΩ)

(a) v2(t)-v1(t)平面上的相轨图 (b) v1(t)与v2(t)时域波形图8 实验测量混沌簇发振荡(R= 34 kΩ)

5 结语

本文在传统的文氏桥振荡器中采用LC滤波器替换并联支路电阻，并用二极管实现耦合，实现了一种新颖的四阶文氏桥振荡器。建立了数学模型，通过数值仿真和实验测试验证了该文氏桥振荡系统存在周期簇发振荡和混沌簇发振荡现象。新提出的文氏桥振荡器具有简单的电路结构，易于物理实现。

[1] Dana S K, Sethia G C, Sen A. Bursting Near homoclinic bifurcation in Two Coupled Chua oscillators[J]. International Journal of Bifurcation and Chaos, 2011, 17(17): 3437 - 3442.

[2] Ji Y, Bi Q S. Symmtric bursting behaviour in non-smooth Chua's circuit[J]. Chinese Physics B, 2010, 19(8): 200 - 204.

[3] Wu H G, Bao B C, Liu Z, Xu Q, et al. Chaotic and periodic bursting phenomena in a memristive Wien bridged oscillator[J]. Nonlinear Dynamics, 2015, 83: 893 - 904.

[4] Li X, Zhang Z D, Bi Q S. Mechanism of bursting oscillations in non-smooth generalized Chua's circuit with two time scales[J]. 2013 Acta Physica Sinica, 62(22): 220502.

[5] Zhou G H, Bao B C, Xu J P. Complex dynamics and fast-slow scale instability in current mode controlled buck converter with constang current load[J]. International Journal of Bifurcation and Chaos, 2013, 23(4): 1350062.

Bursting Phenomenon Analyses and Experimental Validation in Wien-bridge Oscillator

XU Quan, ZHANG Qin-ling, SHI Guo-dong

(SchoolofInformationScienceandEngineering,ChangzhouUniv.,Changzhou213164,China)

Replacing the parallel resistor with a passive LC filter and nonlinear coupling by a diode pair to the parallel bridge arm of classical Wien-bridge oscillator, a novel Wien-bridge oscillator is implemented. The dynamical model is established, upon which the dynamical behavior is performed. The results show that the fast-slow effect existing in the system under given parameter region. Furthermore, the dynamics for chaotic and period bursting phenomena are explained. A hardware realization circuit is built, the experimental circuit has simple structure and is easy to physical manufacture, and the experimental measurements and numerical simulations are consistent, verifying the validity of the theoretical analyses.

periodic bursting oscillate; chaotic bursting oscillate; Wien-bridge oscillator

2016-06-12;

2016-07-30

徐 权(1983-)，男，博士，讲师.主要从事非线性电路与系统的教学和研究，E-mail：xuquan@cczu.edu.cn 张琴玲(1981-)，女，硕士在读，研究方向为非线性电路与系统，E-mail：18115010289@163.com 史国栋(1956-)，男，博士，教授，主要从事非线性电路与系统的教学和研究，E-mail：xuquanwww@163.com

TN271+.6; TP918

A

1008-0686(2016)05-0046-04