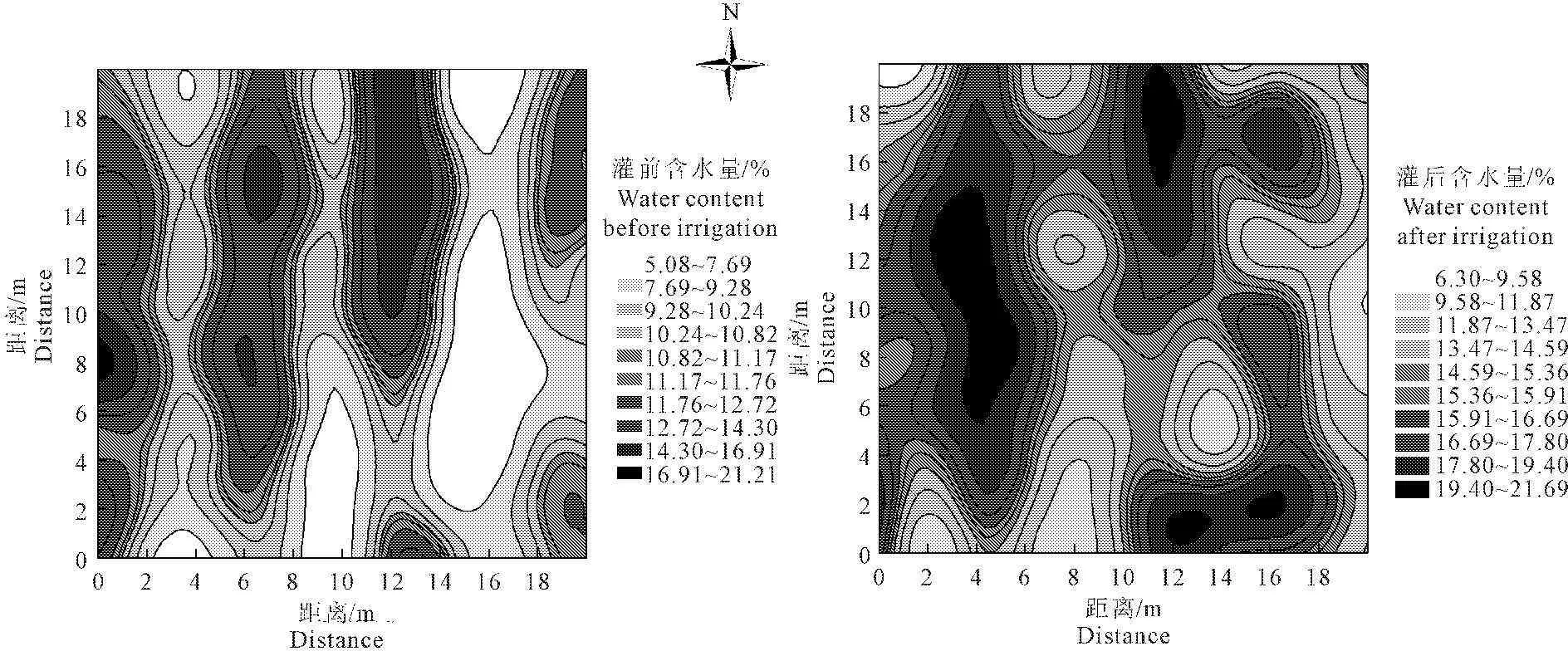
膜下滴灌前后表层土壤水分空间变异性

谭　帅，王全九，罗小东，马　媛

(西北旱区生态水利工程国家重点实验室,西安理工大学， 陕西 西安 710048)



膜下滴灌前后表层土壤水分空间变异性

谭帅，王全九，罗小东，马媛

(西北旱区生态水利工程国家重点实验室,西安理工大学， 陕西 西安 710048)

摘要：以2 m×2 m的网格布点，采用经典统计学和地统计学结合的方法研究了一次灌溉前后膜下滴灌棉田的表层土壤体积含水量的空间变异性特征。结果表明：(1) 灌溉前后表层土壤含水量变异系数(CV)分别为28.7%和21.8%，均表现出中等变异特性，颗粒分布能为灌溉前后表层土壤含水量的变异系数变化提供参考。(2) 灌溉前后表层土壤含水量的半方差函数均可用高斯模型很好地描述(R2>0.9)，对应的空间异质比(C0/(C0+C))分别为0.201和0.324，表现出强烈和中等的空间依赖性；灌溉后，表层土壤含水量空间自相关性减小，4.373 m可作为该研究区域的参考取样步长。(3) 灌溉前后表层土壤含水量的Moran’s I随滞后距离变化的趋势大体一致，且灌前表层土壤含水量的自相关性较灌后显著。(4) Kriging插值结果表明，灌溉前后含水量空间分布较相似，表现出显著的变异性，且灌后含水量分布较灌前复杂。

关键词：膜下滴灌；表层土壤含水量；空间自相关；Kriging

土壤水分是水循环的重要组成部分[1-3]，在土壤-植物-大气(SPAC)过程中起到关键的作用[4]。表层土壤水分决定着水分入渗、径流、蒸发等过程[5]。由于自然因素、地形因素、土壤结构特性、植被因素、农业活动等影响，往往使得土壤水分在空间上存在变异性，其中表层土壤水分分布的变异性尤为明显。

国内外对表层土壤水分变异性的研究很多，大多数研究[6-10]都表明表层土壤含水量具有显著的空间变异特征，而其研究主要集中在中大尺度[6,8]、不同景观模式[6]、地形[7-8]、土地利用方式[9]等方面，而在农业活动(如灌溉、耕作)方面的研究较少，尤其是膜下滴灌下土壤表层水分的变异性研究。由于田间灌溉，必然会造成灌溉前后土壤水分空间分布产生差异，进而对作物生长产生影响。因此，了解灌溉前后土壤表层水分空间分布的变异特征具有重要意义。

在干旱的新疆地区，土壤水分是作物生长发育的主要因素。该地区农田灌溉模式主要以膜下滴灌为主，滴灌属于局部灌溉，加之覆膜使得水分分布更加复杂。为了更好地解释该灌溉情况下土壤-大气边界上水分与能态关系，进而指导当地进行合理灌溉，了解该灌溉模式下表层土壤水分空间分布十分必要。鉴于此，本文采用经典统计和地统计学结合的方法，对20 m×20 m膜下滴灌下棉田进行2 m×2 m网格采样，分析了该灌溉模式下一次灌水前后对表层0～15 cm土层土壤体积含水量空间分布的动态变化的影响，旨为指导农田合理灌溉提供理论基础和参考依据。

1材料与方法

1.1研究区概况

试验区设在巴音郭楞蒙古族自治州巴州重点灌溉试验站。试验站地处亚欧大陆中心，新疆腹地，塔里木盆地北缘，地形较平缓，海拔988～991 m，东经86°09′～86°10′，北纬41°34′～41°35′，地形总趋势为北高南低。多年降水量53.5～62.7 mm，蒸发量2 273～2 788 mm(直径20 cm蒸发皿)，平均气温10.7℃，年日照数3 036.2 h，风速2.4 m·s-1，无霜期144～241 d，地下水埋深为1.37～2.47 m，地下水矿化度为2.98～4.19 g·L-1。该地区干燥少雨且风沙较多、四季分明、冬夏漫长、春秋短暂，属典型的大陆性气候。试验区农田以种植棉花为主，灌溉方式为膜下滴灌，采用一膜两管四行的种植方式，宽行、窄行、膜间距离分别为40 cm、20 cm、30 cm，具有一定代表性[11-12]。滴灌带设计滴头流量为2.7 L·h-1，滴头制造偏差≤10%，滴头间距为30 cm，灌溉水主要来自孔雀河，平均灌水矿化度为0.8 g·L-1。试验区土质以砂土和砂壤土为主。

1.2采样点布置及测定方法

研究所选区域为试验区面积为20 m×20 m的田块，于2013年8月对该区域进行灌溉前后采样，此时处于棉花吐絮期，累积灌溉次数为10次。沿试验区东西和南北方向以2 m×2 m的网格对研究区布点，共设121个测点，取样点包括膜间、窄行及宽行，具有一定代表性。图1为取样点示意图，其中膜间样点33个，窄行样点33个，宽行样点55个。在第11次灌水前后各一天对表层0～15 cm的土壤进行取样，此时正处于棉花吐絮期，棉花耗水较小，此时更能反映田中水分空间分布情况，累积采样242个，灌水前后同一测点的取样点相邻，且灌水期间无降雨。用直径为5 cm的土钻取土，将0～15 cm的土样均匀混合，分为2份分别装入塑封袋和铝盒中。待土样风干后，过2 mm分样筛，用马尔文MS2000激光粒度分析仪测定各取样点的表层土壤的机械组成，根据国际制划分黏粒(<0.002 mm)、粉粒(0.002～0.02 mm)和砂粒(0.02～2 mm)。采用经典烘干法(105℃)测定表层土壤0～15 cm的平均质量含水量(g·g-1)，环刀法(体积为100 cm3)测定表层土壤干容重，然后通过质量含水量和干容重换算出表层土壤体积含水量(cm-3·cm-3)，文中的含水量均为体积含水量。

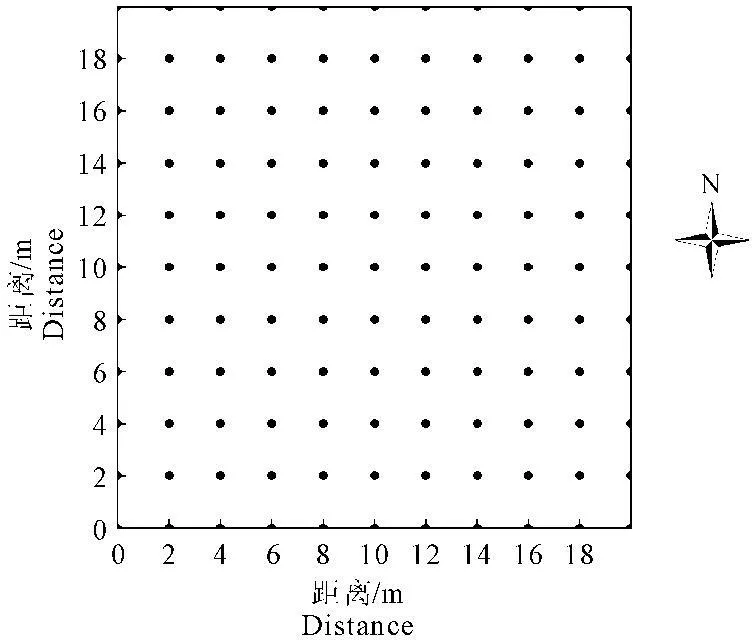
图1取样点布设

Fig.1Layout of sampling points

1.3经典统计学分析

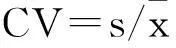
(1)

1.4半方差函数

半方差函数能在一定范围内反映不同观测点的观测值之间关系的空间依赖情况，描述各观测指标的空间变异结构及基本规律[13-14]。半方差函数反映了测定区域所考察地域化变量的空间变异结构，在确定土壤参数合理取样数和克里格插值计算中起着重要的作用[15]。估算半方差的公式为

(2)

式中，h为两样本点空间分隔距离或滞后距离；N(h)为滞后距离为h时的样本对数；Z(xi)和Z(xi+h)为随机变量Z在空间位置xi和xi+h上的观测值。描述单一尺度空间变异特征的半方差模型分为线性、球形、指数和高斯模型[16]。一般情况下，半方差函数在最大间隔的1/2内才有意义，故本文中半方差函数的有效滞后距(Activelag)均设为最大采样间距的1/2[17]。

文中对半方差函数主要采用高斯模型拟合，其公式为

(3)

式中，C0为块金值(Nugget)，表示随机变异的大小，包括最小取样间隔内自然过程产生的变异以及试验误差；C是结构方差，表示由土壤母质、地形及气候等非人为因素造成的变异；h为滞后距离；a为变程。当h越大时，半方差γ(h)将趋向于一个极限值C0+C，即基台值(Sill)，表示变量在研究区域的总变差。一般用[C0/(C0+C)]表示空间异质性程度，反映随机变异占总变异的大小[18]，大小在0～1之间。根据Cambardella[19]划分标准，C0/(C0+C)≤25%时表现为强烈的空间依赖性；25%

1.5局部Moran's I

Moran's I是由Moran于1948年提出，随后在1995年Anselin提出局部Moran指数来反映每一个空间单元与邻近单元某一属性的相似程度，其值介于-1到1之间，大于0表示正相关，小于0则表示负相关，等于0表示不相关，取决于相关的程度和方向[20]。

(4)

1.6数据处理

用SPSS 19.0对样本数据作描述性统计学分析；采用GS+9.0对数据进行地统计分析；利用ArcGIS 9.3进行克里格(Kriging)插值，绘制表层土壤水分分布图。

2结果与分析

2.1灌溉前后表层土壤含水量统计特征

表1显示了滴灌棉田表层土壤含水量的统计特征值。由表可知，灌水前表层土壤含水量在5.08%～21.21%范围内变化，且处于萎蔫系数(6.24%)与田间持水量(23.7%)之间。灌溉结束后，滴灌灌水增加了土壤中水分含量，表层土壤含水量在6.30%～21.69%范围内变化，平均表层土壤含水量相对灌前增加45.9%。通过Kolmogorov-Smirnov (K-S)检验可知，灌前和灌后表层土壤含水量均服从正态分布。

表1　表层土壤含水量统计特征值

注：表中含水量均为体积含水量(cm-3·cm-3)，下同。N表示正态分布。

Note: Water content in the table are volumetric water content (cm-3·cm-3) and the same below. N expresses normal distribution.

研究表明[3,5-6]，由于气象、微地形、灌水施肥方式等因素影响，土壤水分平均含量必然存在差异。因此，滴灌灌溉后，表层含水量的变异程度也会存在差异。根据Nielsen划分标准，灌前和灌后表层土壤含水量的变异系数分别为28.7%和21.8%，均表现为中等变异性。这与徐英[21]、李彦[22]、李芳松[23]和李敏[24]等的研究结果相一致。灌水结束后，表层土壤含水量的CV减小，这与Hu等[8]、刘丙霞等[4]、佘冬立等[25]及张继光等[7]在干湿条件下表层水分变化的研究结果具有一致性，但与李芳松等[23]的研究结果有所差异。原因可能是其研究区域滴灌带布置为一膜一管四行，加之其取样仅为一个膜内，研究地点不同进而造成土壤土质、气象、地形等情况不同，也可能造成结果不一致。

土壤含水量不仅受气象、地形等因素的影响，还受土壤特性的影响，特别是土壤颗粒组成的影响[26-27]。Hu等提出由于土壤颗粒分布不同，土壤水分变异性能反映出土壤孔隙的变异程度，相反地不同土壤粒径大小或许能够解释体积含水量变异情况[8]。为进一步分析表层土壤含水量的变异性，对各样点的土壤颗粒组成进行统计分析(表2)。由表2可知，黏粒、粉粒和砂粒的CV值分别为10.7%、10.5%和3.7%，说明除砂粒呈弱变异性外，黏粒和粉粒均呈中等变异性，其中黏粒的变异程度最大。

表2　颗粒组成的均值和变异系数

一般来说，土壤中小孔隙大多由粒径较小的颗粒组成，在干旱情况下，小孔隙能储存较多的水分。为了能更好阐述水分与颗粒组成间的关系，对灌溉前后含水量与颗粒组成进行了相关性分析(表3)。由表3可知，灌溉前后含水量与黏粒的相关性差异较明显(灌前0.299，灌后0.232)，与粉粒、砂粒两者间的相关性差异不明显，说明黏粒含量可能是影响水分分布的主要因素。由表3可知灌前表层土壤含水量随黏粒含量的变化幅度较灌后明显，而在颗粒组成中，黏粒的变异程度最大，可能使得灌前表层含水量较灌后的变异程度大，这为解释该区域灌后表层土壤水分CV值呈减小趋势的变化提供参考依据。Baroni等[10]的研究表明在土壤湿润的条件下，土壤含水量变异性与土壤质地有一定关系，而在土壤干旱条件下，土壤含水量受植被因素的影响较大。Gonzalo等[28]发现在干燥条件下土壤含水量的变异是土壤水力特性和气象因素共同作用的结果。Baroni和Gonazlo的研究结果均与本文中灌前(干旱)表层土壤含水量与土壤质地有一定关系不一致，原因可能是研究区域、湿润方式、植被影响程度等方面也存在差异。因此，除了土壤质地的影响因素，植被因素(如叶面积、株高等)、气象因素、土壤水力参数等对土壤水分影响也需进行深入研究。

表3　土壤参数Pearson相关性分析

注：**表示P<0.01的极显著水平。Note: ** Significant level atP<0.01.

2.2灌溉前后表层土壤水分空间地统计学分析

2.2.1半方差分析为进一步反映滴灌棉田土壤表层含水量的空间结构性，应用GS+9.0地统计学软件在不考虑各向异性的情况下，分别对灌溉前后表层土壤含水量进行半方差分析，通过决定系数(R2)和残差(RSS)选择最优半方差函数模型对其进行拟合，表4为最优半方差函数参数，图2为灌溉前后表层土壤含水量的半方差图。

表4　土壤表层含水量半方差函数参数

图2灌溉前后表层含水量的半方差

Fig.2The variogram for surface layer water

content before and after irrigation

由表4可知，灌前和灌后含水量的最优拟合模型均为高斯模型，各项的残差平方和(RSS)均较小，决定系数R2均在90%以上，说明高斯模型能较好地描述试验半方差函数与滞后距离之间的关系。

灌溉前后表层土壤含水量的块金值(C0)分别为1.95和3.50，表明无论在灌前还是灌后表层土壤含水量具有块金效应，说明在低于试验取样尺度(2 m)下有影响表层水分分布结果的作用存在。灌后块金值较灌前大，这与张继光等[7]在喀斯特地区和佘冬立等[27]在黄土高原研究干湿条件下表层含水量的结果类似。基台值(Still)同样表现为灌后大于灌前，这与张继光等[7]和佘冬立等[27]的研究结果不同，原因可能是一方面由于研究区域不同，导致气候、土质、植被覆盖条件等因素不同；另一方面其研究分别为喀斯特地形和坡地，从而使得表层土壤水分分布存在差异；加之，湿润情况主要为滴灌灌溉在局部性影响下的水分分布，而黄土高原和喀斯特地区的湿润情况主要是由降雨影响，具有整体性，与本研究区域存在一定差异。

由表4可知，灌溉前后表层土壤含水量由随机因素引起的空间异质性(C0/(C0+C))分别为20.1%和32.4%，主要体现在2 m以下的尺度上，而灌溉前后表层含水量由空间自相关引起的空间异质性占总空间异质性的79.9%和67.6%，该差异主要表现在取样间隔(2 m)到变程的(4.573 m和4.347 m)尺度上。根据Cambardella[19]划分标准，灌前表层土壤含水量表现出强烈的空间依赖性，而灌后表层含水量表现出中等空间依赖性。灌后表层土壤含水量的空间异质比增加，表明随机因素(灌水、施肥等)引起的变异概率增加，而受自身结构(如土壤结构、微地形、土壤物化性质、地温等)产生的变异概率减小。

灌溉前后表层含水量的变程(a)分别为4.573 m和4.347 m，表明灌水结束后，含水量半方差函数对应的a较灌水前减小，反映水分空间连续相对变小，随机变异性增加，这与其空间异质比的变化是相对应的。原因可能是灌水前土壤表层水分就存在着差异，土壤结构的不均匀性就已使得区域内各处保持水分的能力不同，加之滴灌和覆膜，可能使得灌水后研究田块内水分分布差异性更大，从而导致含水量变异性增加。另一方面，a可以反映最大相关距离，可通过a优化采样间距，从而减少取样点数，可用4.347 m作为参考来优化灌溉对该区域水分变异性影响的采样间距。

2.2.2空间自相关性分析为确定土壤含水量在空间上的相关程度，引入局部Moran's I来定量描述表层土壤含水量在空间上的依赖关系。图3显示了表层土壤含水量的局部Moran's I与滞后距离的关系，可以看出随滞后距离增大，灌溉前后的表层含水量的局部Moran's I随滞后距离的变化大体一致，表现为波动性减小的趋势，说明土壤表层水分具有一定的空间结构，呈较简单的斑块状分布。当滞后距离处于采样间距(2 m)与变程(灌前4.573 m、灌后4.347 m)之间，局部Moran's I为正值，说明灌溉前后表层土壤含水量具有显著的空间正相关，主要表现为高含水量向高含水量集聚，低含水量向低含水量集聚，灌前相似的表层土壤含水量空间集聚性较为明显；随滞后距离增加，Moran's I减小，表明灌溉前后表层土壤含水量的自相关性减小。当滞后距离处于变程与7.5 m间时，局部Moran's I仍为正值，但变化较小，说明灌溉前后表层土壤含水量的集聚性差异不明显；当滞后距离增加到7.5 m左右，局部Moran's I接近于0，表现为灌溉前后表层土壤含水量空间不相关，说明变量呈随机分布，无规律性；当滞后距离大于7.5 m时，局部Moran's I向负方向延伸，整体达到显著的空间负相关，表现为高含水量向低含水量集聚，而低含水量向高含水量集聚，变量趋于分散分布。

图3灌溉前后表层土壤含水量的Moran's I

与滞后距离的关系

Fig.3The relationship between Moran's I and lag distance

for surface layer soil water before and after irrigation

2.3基于Kriging插值空间分布格局

Kriging插值是无偏预测中最好的插值方法，但做分位图和概率图时，数据必须服从正态分布，否则会存在比例效应和不稳定性。故本文采用Kriging插值方法对表层土壤含水量进行预测。

通过ArcGIS 9.3对灌溉前后表层土壤含水量进行插值，绘制其空间分布图(图4)。从图4可知，灌水后含水量增加，并且从斑块大小和颜色深度不同反映出灌溉前后的表层土壤含水量表现出明显的空间变异性，灌后表层含水量分布较灌前复杂，即灌后较灌前斑块多且含水量高低差异较明显，并且还可以看出无论是灌前还是灌后，较高的表层土壤含水量和较低的表层土壤含水量均相对集中，即较高表层土壤含水量集中于膜下(宽行和窄行处)，较低表层土壤含水量集中于膜间处。由图4可知，灌水前较高表层土壤含水量的斑块位置在灌水后仍处于较高值，并且逐渐向四周扩散。原因可能是较高表层土壤含水量的位置大部分集中于膜下，而膜间与膜下表层土壤含水量差异较大，使得膜下与膜间存在水势梯度，因此水分向两侧横向扩散。

图4表层土壤含水量空间分布

Fig.4The spatial distributions of surface layer soil water content

3讨论

在干旱区，土壤含水量是作物生长发育的主要限制因素，表层含水量在水分蒸发、入渗等过程中起着关键的作用，了解表层含水量空间分布具有重要意义。加之为实现在干旱区达到高效节水和防治盐碱地的目的，膜下滴灌灌溉农田的灌溉方式使用较为广泛，而由于局部灌溉和覆膜的复杂性，必然会造成滴灌前后的表层含水量的分布有所差异。

本文研究表明，灌溉前后表层土壤含水量均具有不同程度的变异性。通过经典统计学分析表明灌溉后表层土壤含水量的CV值减小，而地统计学表明空间依赖性减小。这与前人[4,7-8,10,21-25,28]的研究结果较为一致，研究虽具有相似性，并且部分研究是在膜下滴灌条件下进行的测定[21-24]，但由于管道布设方式与测定地区的不同，使得水分分布存在部分差异；加上部分研究是基于次降雨的干湿交替下[4,7-8,25]和不同地形条件下(坡地[4,8]、喀斯特地区[7,27])测定得到的结果，也会造成水分分布出现不同。而农田表层含水量空间分布情况是受到气象、微地形、作物吸水、土壤孔隙、灌水施肥模式等多方面因素的综合影响结果。因此，各种影响因子对农田表层含水量的影响究竟如何仍需进一步探究。

4结论

本文通过空间小尺度网格布点对一次滴灌前后棉田表层含水量空间变异性进行了研究，主要得到以下结论：

1) 灌水前后含水量均表现为中等变异特性且呈正态分布，但灌溉结束后，含水量变异系数减小。颗粒组成的变异特点可能为研究区域灌后含水量变异系数的减小提供一定解释。

2) 灌溉前后含水量的半方差函数均能用高斯模型很好地描述，分别表现出强烈和中等的空间依赖性，且灌后含水量的空间自相关性有一定程度的减小，灌后块金值、基台值及空间异质比较灌前增加，但变程减小。采用4.347 m作为参考采样间距能优化该研究区域的取样步长。

3) 灌溉前后的表层含水量空间自相关性变化大体一致，具有明显的空间结构性，且灌前表层土壤含水量的相关性较灌后的高。

4) Kriging插值结果表明，灌前和灌后含水量变化具有一定程度的相似性，且表现出明显的变异性。

参 考 文 献：

[1]Heathman G C, Cosh M H, Han E, et al. Field scale spatiotemporal analysis of surface soil moisture for evaluating point-scale in situ networks[J]. Geoderma, 2012,170:195-205.

[2]Martínez-Fernández J, Ceballos A. Mean soil moisture estimation using temporal stability analysis[J]. Journal of Hydrology, 2005,312(1):28-38.

[3]Brocca L, Melone F, Moramarco T, et al. Soil moisture temporal stability over experimental areas in Central Italy[J]. Geoderma, 2009,148(3):364-374.

[4]刘丙霞,邵明安.黄土区退耕草地小尺度土壤水分空间异质性[J].中国水土保持科学,2012,10(4):60-65.

[5]Weiherm Ller L, Huisman J A, Lambot S, et al. Mapping the spatial variation of soil water content at the field scale with different ground penetrating radar techniques[J]. Journal of Hydrology, 2007,340(3):205-216.

[6]Mohanty B P, Skaggs T H, Famiglietti J S. Analysis and mapping of field-scale soil moisture variability using high-resolution, ground-based data during the Southern Great Plains 1997 (SGP97) Hydrology Experiment[J]. Water Resources Research, 2000,36(4):1023-1031.

[7]张继光,陈洪松,苏以荣,等.湿润和干旱条件下喀斯特地区洼地表层土壤水分的空间变异性[J].应用生态学报,2006,17(12):2277-2282.

[8]Hu W, Shao M A, Wang Q J, et al. Soil water content temporal-spatial variability of the surface layer of a Loess Plateau hillside in China[J]. Scientia Agricola, 2008,65(3):277-289.

[9]郭德亮,樊军,米美霞.黑河中游绿洲区不同土地利用类型表层土壤水分空间变异的尺度效应[J].应用生态学报，2013,24(5):1199-1208.

[10]Baroni G, Ortuani B, Facchi A, et al. The role of vegetation and soil properties on the spatio-temporal variability of the surface soil moisture in a maize-cropped field[J]. Journal of Hydrology, 2013,489:148-159.

[11]单鱼洋.干旱区膜下滴灌水盐运移规律模拟及预测研究[D]．北京：中国科学院研究生院，2012.

[12]刘建军.棉田膜下滴灌条件下土壤水盐分布特征试验研究[D]．西安：西安理工大学,2009.

[13]邵明安,王全九,黄明斌.土壤物理学[M].北京:高等教育出版社，2006.

[14]何丹.封丘地区土壤水分入渗特性的时空变异及其影响因素研究[D]．雅安：四川农业大学,2012.

[15]秦耀东.土壤空间变异研究中的半方差问题[J].农业工程学报,1998,14(4):42-47.

[16]王政权.地统计学及在生态学中的应用[M].北京:科学出版社,1999.

[17]张川,陈洪松,张伟,等.喀斯特坡面表层土壤含水量、容重和饱和导水率的空间变异特征[J].应用生态学报,2014,25(6):1585-1591.

[18]王云强,张兴昌.黄土区小尺度坡面土壤含水率时空变异性研究[J].水土保持学报,2008,22(2):32-37.

[19]Cambardella C, Moorman T, Parkin T, et al. Field-scale variability of soil properties in central Iowa soils[J]. Soil Science Society of America Journal, 1994,58(5):1501-1511.

[20]张松林,张昆.空间自相关局部指标Moran指数和G系数研究[J].大地测量与地球动力学,2007,27(3):31-34.

[21]徐英,陈亚新,史海滨,等.土壤水盐空间变异尺度效应的研究[J].农业工程学报,2004,20(2):1-5.

[22]李彦,雷晓云,申详民,等.膜下滴灌条件下土壤水分空间分布特征研究[J].水资源与水工程学报,2010,21(6):4-7.

[23]李芳松,雷晓云,陈大春,等.膜下滴灌棉田土壤水分空间变异规律研究[J].灌溉排水学报,2010,29(6):68-71.

[24]李敏,李毅,曹伟,等.不同尺度网格膜下滴灌土壤水盐的空间变异性分析[J].水利学报,2009,40(10):1210-1218.

[25]佘冬立,邵明安,俞双恩.黄土区农草混合利用坡面土壤水分空间变异性[J].农业机械学报，2010,41(7):57-63.

[26]张永萱,张光辉,王志强.黄土剖面土壤颗粒组成对土壤含水量的影响[J].水土保持通报,2009,29(6):6-9，15.

[27]Grayson R B, Chiew F H S, BL SCHL G. Preferred states in spatial soil moisture patterns: Local and nonlocal controls[J]. Water Resources Research, 1997,33(12):2897-2908.

[28]Gonzalo Martínez García, Yakov A. Pachepsky, Harry Vereecken. Effect of soil hydraulic properties on the relationship between the spatial mean and variability of soil moisture[J]. Journal of Hydrology, 2014,516(SI):154-160.

The variability of surface layer soil water content under

plastic mulch dripping before and after irrigation

TAN Shuai, WANG Quan-jiu, LUO Xiao-dong, MA Yuan

(StateKeyLaboratoryBaseofEco-HydraulicEngineeringinAridArea,Xi’anUniversityofTechnology,Xi’an,Shaanxi710048,China)

Abstract：In this research, classical statistics and geostatistics were combined to research the characteristics of spatial variability for surface layer soil water content in a area of 20 m×20 m cotton field by dripping under mulch before and after the irrigation. The primary results showed that the variation coefficients (CV) for surface layer soil water before and after irrigation were 28.7% and 21.8%, respectively, exhibiting moderate variability. The particle distribution could provide a basis for the variations inCVof water content before and after irrigation. Additionally, the semivariogarm function for surface layer soil water content before and after irrigation could be described well by Gaussian model (R2). The corresponding ratios of spatial heterogeneity (C0/(C0+C)) were 0.201 and 0.324, respectively, indicating strong and moderate spatial dependences, respectively. After irrigation, the spatial autocorrelation of surface layer soil water content became decreased. The reference sample step lag of study region could be adopted by 4.373 m. Moreover, Moran’s I for surface layer soil moisture before and after irrigation followed similar trends with the lag distance. The autocorrelation of surface layer soil water content before irrigation was more significant than that after irrigation. Lastly, the results of Kriging interpolation showed that spatial distributions for water content before and after irrigation were similar and showed obvious variabilities. Water content after irrigation was more complex than that before irrigation.

Keywords:plastic mulch drip irrigation; surface layer soil water content; spatial correlation; Kriging

中图分类号：S275.6；S152.7

文献标志码：A

通信作者：王全九(1964—)，男，教授，博士生导师，主要从事农业水土工程与生态环境方面的研究。 E-mail: wquanjiu@163.com。

作者简介：谭帅(1990—)，女，湖南衡阳人，硕士研究生，主要从事农业水土资源与生态环境方面的研究。 E-mail:tans90@163.com。

基金项目：水利部公益性行业科研专项经费项目(201301102)；新疆维吾尔自治区科技计划项目(201130103-3)；国家自然基金(51409212，51409213)；博士后基金(2014M562525XB)

收稿日期：2015-04-05

doi:10.7606/j.issn.1000-7601.2016.01.07

文章编号：1000-7601(2016)01-0043-07