遗传算法优化的非线性钢结构模糊控制研究
2016-03-01张永兵梁星云陈立星
张永兵,梁星云,唐 滢,陈立星
(广西大学土木建筑工程学院, 广西南宁530004)
遗传算法优化的非线性钢结构模糊控制研究
张永兵,梁星云,唐滢,陈立星
(广西大学土木建筑工程学院, 广西南宁530004)
摘要:采用遗传算法优化模糊控制算法的隶属函数及比例因子,通过压电变摩擦阻尼器实现减少非线性钢结构的地震响应。采用双输入单输出的模糊控制器,选取结构的层间位移的绝对值、层间速度的绝对值作为模糊控制器的输入变量,输出变量为作用电压,选取三角形函数作为输入、输出变量的隶属度函数,使用遗传算法对隶属函数及比例因子做出优化。以3层非线性钢结构地震响应为例,分别对模糊控制算法及遗传算法优化后模糊控制算法进行数值分析,结果表明:经遗传算法优化后的模糊控制,进一步降低了非线性钢结构的加速度和位移等响应。
关键词:钢结构;振动控制;模糊控制;遗传算法
0引言
我国是个地震多发国家,如何减少地震对建筑结构的破坏是一个重要的研究课题。对结构进行振动控制研究是国内外的研究热点。
利用压电材料制作压电变摩擦阻尼控制装置,结合合理的控制算法,可以有效地降低建筑结构在地震作用下的响应,国内外的很多学者进行了深入研究。Kamada等[1]应用多层式压电陶瓷驱动器对4层钢框架模型进行控制;杨飏等[2]提出压电摩擦阻尼器,对两自由度结构进行了半主动控制研究;瞿伟廉等[3]设计了压电材料智能摩擦阻尼器,对高耸塔结构风振进行了LQR控制研究;张永兵等[4-6]设计了一款新型压电变摩擦阻尼器,采用模糊控制、变增益模糊控制和自协调模糊控制等控制算法对3层及20层钢结构的非线性减振控制进行了研究。
由于模糊系统较依赖于专家经验,可以应用遗传算法来优化模糊控制,改善效果。Shook等[7]利用遗传算法对3层钢结构的模糊控制器进行了优化,控制系统的效果有了显著提升;汪权等[8]采用遗传算法优化模糊规则库,对3层和6层框架结构进行了数值仿真分析;郑伟等[9]采用遗传算法优化模糊规则库,对高层建筑风振进行了仿真分析。
本文选择压电变摩擦阻尼器作为作动器,通过遗传算法对所设计的模糊控制算法中的比例因子、模糊控制的隶属函数进行了优化,实现对地震作用下的3层非线性钢结构的减振控制,有效降低结构的响应。
1模糊控制
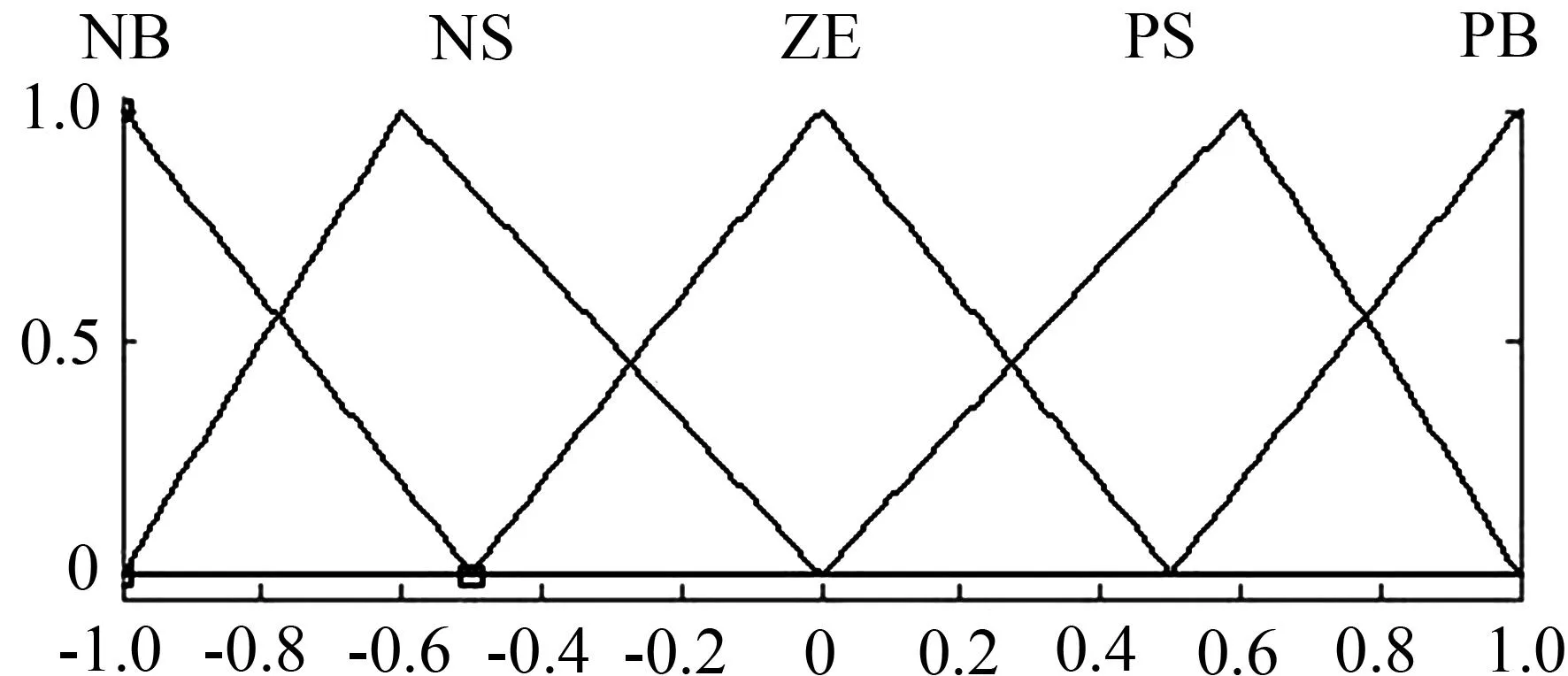
本文选择文献[4]制作的压电变摩擦阻尼器作为半主动控制器。在模糊逻辑控制器的模型中,采用双输入单输出的模糊控制器。选取了结构的层间位移的绝对值、结构的层间速度的绝对值作为模糊控制器的输入变量,输出变量为作用电压。在隶属度函数的选用上,使用三角形函数作为输入、输出语言变量的隶属度函数,各个输入变量和输出变量定义为五个量级:PS(正小),NS(负小),ZE(零),NB(负大),PB(正大)。结构层间位移绝对值的隶属度函数和层间速度绝对值隶属度函数分别见图1和图2,输出电压的隶属度函数见图3,模糊控制规则见表1。本模型中利用的模糊推理算法为Mamdani推理法,解模糊法选用加权平均法。增加位移量化因子和速度量化因子两个参数,位移量化因子将输入的每一楼层的最大位移的绝对值变换到输入的模糊论域中,速度量化因子同理。电压比例因子用于将模糊控制器的输出量转化为作用电压。本文中,位移量化因子选用各楼层位移绝对值的最大值的倒数,速度量化因子选用各楼层速度绝对值的最大值的倒数,根据以往经验,可以达到比较好的效果[4],电压比例因子选用100。

图1输入位移的隶属函数
Fig.1Membership functions of displacement

图2输入速度的隶属函数
Fig.2Membership functions of velocity
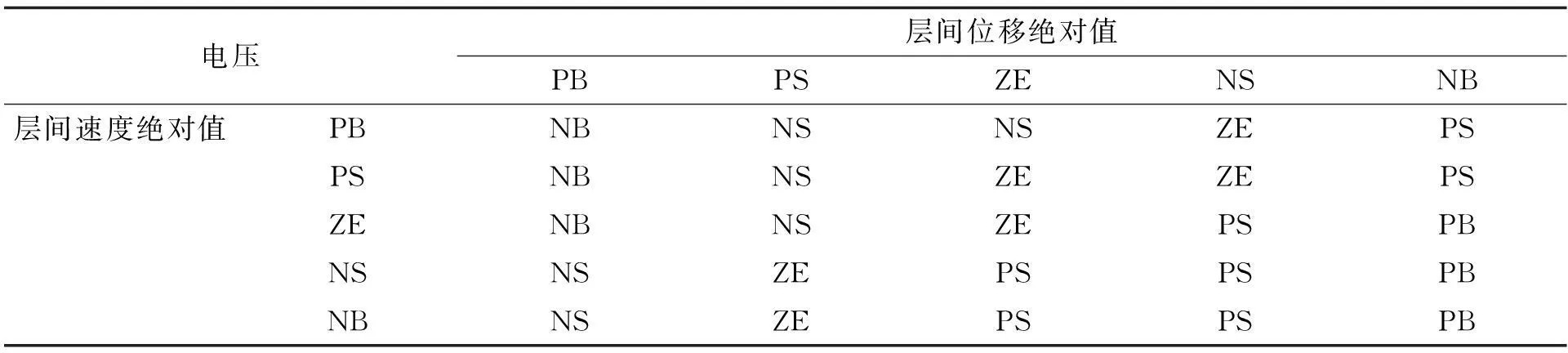
电压层间位移绝对值PBPSZENSNB层间速度绝对值PBNBNSNSZEPSPSNBNSZEZEPSZENBNSZEPSPBNSNSZEPSPSPBNBNSZEPSPSPB
2遗传算法优化模糊控制
2.1编码
本文利用遗传算法对所设计的模糊控制算法中的电压比例因子、模糊控制的隶属函数进行了优化改进,使用浮点数编码方法。编码被串接成一个染色体组,遗传算法程序将会不断优化这个染色体组,以期得到更好的数据,使用变量m1~m8来描述位移、速度、电压三个隶属度函数中的变量,如图4和图5所示。
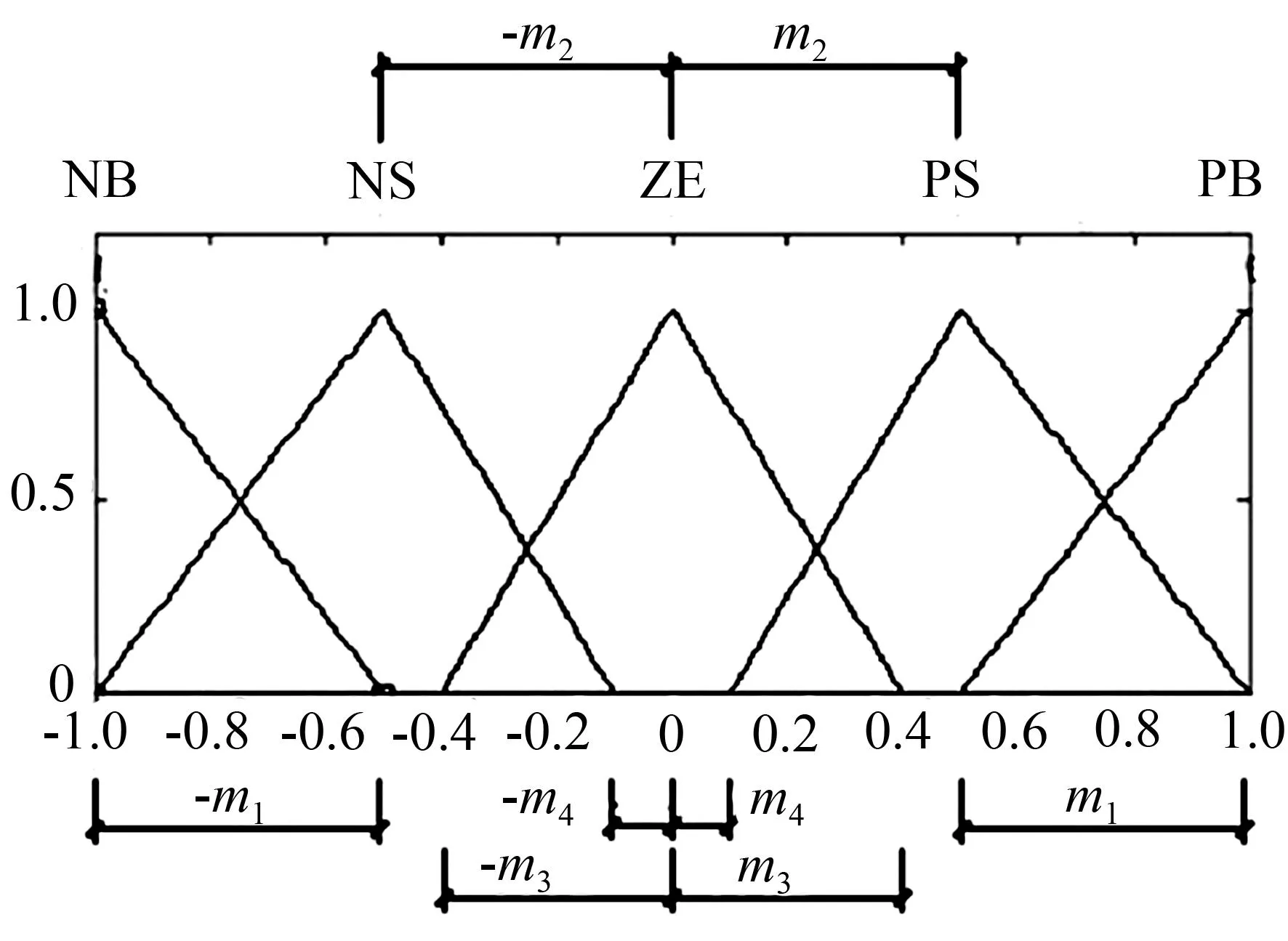
图4优化设计速度和位移的隶属度函数
Fig.4Ga-optimizing membership functions of
velocity and displacement
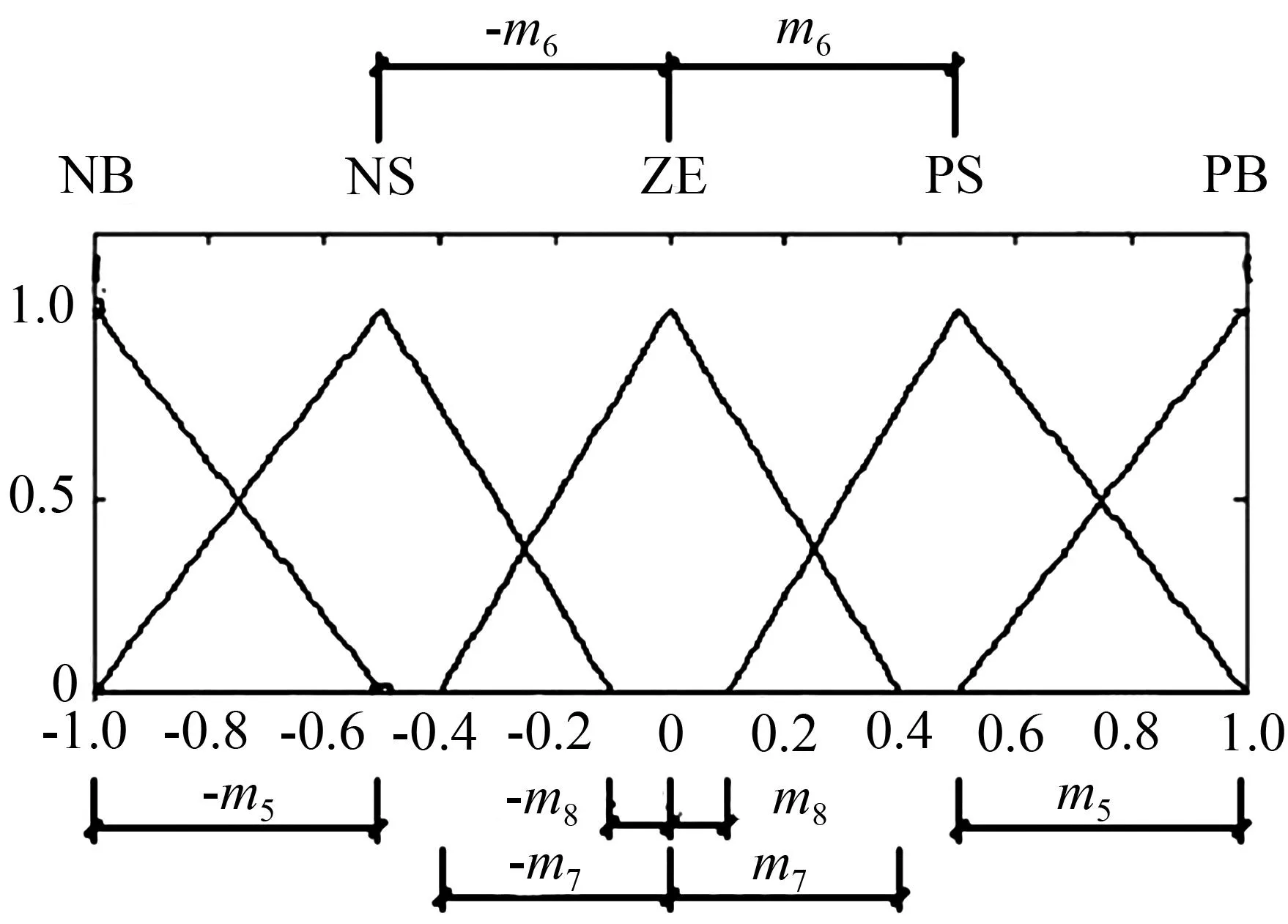
图5优化设计输出电压的隶属度函数
Fig.5Ga-optimizing membership
functions of voltage
为了便于运用遗传算法进行优化,对控制器的电压比例因子进行编码,用变量K1,K2和K3分别表示第1层、第2层和第3层的电压比例因子。
2.2设置初始种群
经过编码后,初始种群的设置参数决定了遗传算法的复杂性[10]。本文首先确定了浮点数编码部分的待优化变量有11个。为了减小遗传算法搜索空间和缩小范围,尽快的确定最优解,遗传算法的定义需要对变量设定边界条件,如表2所示。

表2 初始种群边界条件
2.3适应度函数设计
适应度函数影响遗传算法的使用功能,是下一步运算的基础[11]。本文优化的目的是使结构在地震作用下的位移响应等指标保持在合理范围内,以结构的最大位移作为评价控制器的性能指标,最大位移可能出现在任何一层,用式(1)来表示:

(1)
式中s是地震作用下钢框架某时刻的最大位移。
2.4选择运算
选择算子是遗传算法的关键[12]。本文应用的选择算子是轮盘赌选择,个体的适应度越高,选入的几率也就越大,具体可用式(2)表示:

(2)
其中:n代表了群体的总数,fi为群体中i个体的适应度,Pi代表i个体被选择的概率。
2.5交叉、变异运算
遗传算法的交叉运算就是匹配两个相应的染色体且进行基因交换,繁衍出下一代个体。染色体是经过选择操作筛选过的高适应度染色体。本文采用对位交叉算法。交叉运算能繁衍出新的基因型和不同于前一代的个体。
之前叙述的选择运算和交叉运算主要是说继承基因的问题。变异运算是在适应度高的基因的后代里改变少量基因,产生少数异种。本文的变异运算使用自适应变异方法。随着进化进程的不断进行,使变异率随之减小,这能保证变异运算不会太快收敛。在实际模拟过程优化模糊控制中的比例因子和隶属函数中,变异很容易产生波动,使得数据不稳定或者朝着错误的方向收敛。可以用式(3)来确定变异率,保持优良个体,防止其被改变。
Pn=0.01-Sn×0.01/S,
(3)
其中:Sn代表当前进化代数,S代表进化总代数,Pn是当前的变异率。
3算例
3.1仿真模型
本算例所使用模型是3层非线性钢框架结构[13]。3层非线性钢框架结构中,每一层安装一个压电变摩擦阻尼器。对遗传算法中各参数的初始设置:初始种群个数为30个,种群迭代代数为75代,选择概率为75%,交叉概率为45%,变异概率为10%。
3.2仿真结果
经过Matlab模拟仿真,模糊控制系统中第1、2、3层的电压比例因子K1、K2、K3优化后分别由100变为131、140、127。利用遗传算法优化结果导出的模糊控制的隶属函数如图6,图7和图8所示。将遗传算法优化所得的隶属函数应用于模糊控制系统中,结构在EI Centro波作用下顶层的位移响应及速度响应分别如图9和图10所示,结构的峰值位移如表3所示。

图6遗传算法优化之后的位移隶属函数
Fig.6Membership functions for displacementafter
genetic algorithm optimization

图7遗传算法优化之后的速度隶属函数
Fig.7Membership functions for velocity after
genetic algorithm optimization

图8 遗传算法优化之后的电压隶属函数


图9 EI波作用下3层位移时程曲线
1.控制率=(无控结构响应峰值-受控结构响应峰值)/无控结构响应峰值。
从图9和图10可知,在EI波的作用下,钢结构3层的峰值加速度,不受控制时为7.397 m/s2,使用模糊控制时时为3.207 m/s2,使用遗传算法优化的模糊控制时为1.822 m/s2,优化后的模糊控制控制率为75.4%;钢结构3层的峰值位移,无控时为0.164 5 m,使用模糊控制时为0.058 1 m,使用遗传算法优化的模糊控制时为0.034 2 m,优化后的模糊控制控制率为79.2%。说明经过遗传算法优化后的模糊控制系统,其参数更加合理,控制效果也更加明显。
结构在Hachinohe波作用下顶层的位移响应及速度响应分别如图11和图12所示,结构的峰值位移如表4所示。

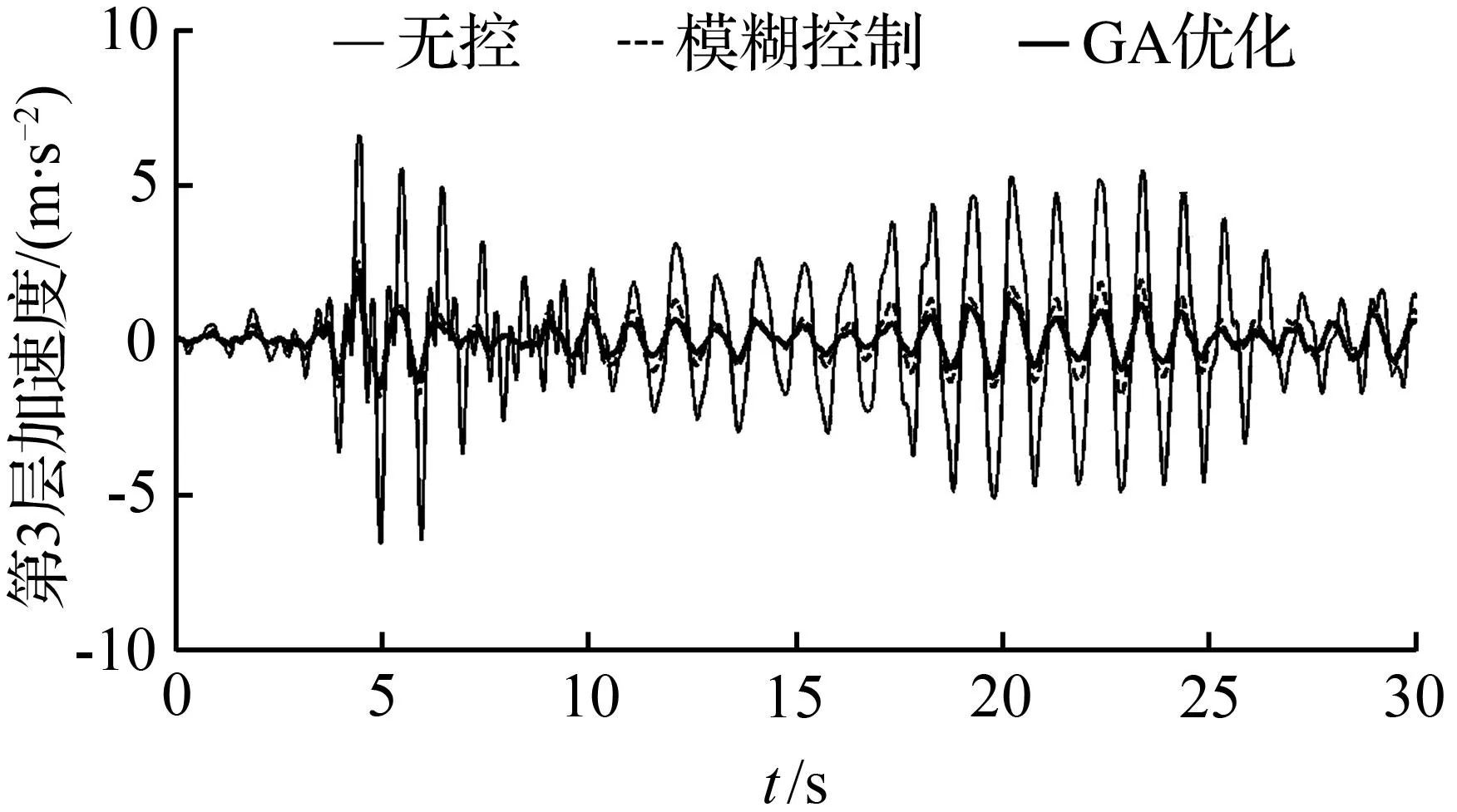
图11 Hachinohe波作用下3层位移时程
从图11和图12可以看出,在Hachiohe波的作用下,钢结构3层的峰值加速度,不受控制时为6.606 m/s2,模糊控制时为2.781 m/s2,使用遗传算法优化的模糊控制时为2.249 m/s2,优化后的模糊控制控制率能达到66.0%;钢结构3层的峰值位移,无控时为0.153 6 m,模糊控制时为0.053 1 m,使用遗传算法优化的模糊控制时为0.040 1 m,优化后的模糊控制控制率能达到73.9%。同EI波的作用下情况相似,经过优化后,模糊控制更合理,控制效果也更好。
4结语
本文选择压电变摩擦阻尼器作为作动器,通过遗传算法对所设计的模糊控制算法中的比例因子、模糊控制的隶属函数进行了优化,并将遗传算法优化后的模糊控制应用于设置了压电变摩擦阻尼器的3层非线性钢框架结构的振动控制中。从算例中得出的结果中,经过遗传算法优化后的模糊控制,相对于研究人员凭经验来设计参数的模糊控制,钢结构的加速度和位移响应有了明显的改善,取得了很好的减振的效果。
参考文献:
[1]KAMADA T, FUJITA T, HATAYAMA T, et al. Active vibration of frame structures of shear and bending type with smart structure using piezoelectric actuator[J]. Smart Structures and Materials, 1997, 3041(1): 75-86.
[2]杨飏,欧进萍.压电变摩擦阻尼器减振结构的数值分析[J].振动与冲击,2005,24(6):1-4.
[3]瞿伟廉,陈朝晖,徐幼麟.压电材料智能磨擦阻尼器对高耸钢塔结构风振反应的半主动控制[J].地震工程与工程振动,2000,20(1):94-99.
[4]张永兵,秦荣,李双蓓.压电变摩擦阻尼器对高层建筑非线性地震反应的模糊控制算法[J].振动与冲击,2008,27(11):142-146.
[5]张永兵,秦荣,李双蓓.3层钢结构非线性地震反应的变增益模糊控制[J].振动与冲击,2008,27(10):106-111.
[6]张永兵,李双蓓,吴炯,等.压电变摩擦阻尼结构的模糊控制[J].广西大学学报(自然科学版),2009,34(1):17-21.
[7]SHOOK D A, ROSCHKE P N, LIN P Y,et al. GA-optimized fuzzy logic control of a large-scale building for seismic loads [J]. Engineering Structure,2008, 30(2): 436-449.
[8]汪权,王建国.建筑结构地震响应半主动控制的遗传—模糊算法[J].地震工程与工程震动,2010,30(6):127-133.
[9]郑伟,阎石.基于遗传算法优化的高层建筑风振模糊控制[J].地震工程与工程震动,2009,29(4):178-182.
[10]乔孟丽,张景元,温莹莹.一种基于遗传算法的模糊控制规则的优化方法[J].计算机测量与控制,2006,14(10):1349-1351.
[11]宋雨,陈卫东,张锦.高速列车半主动悬挂系统遗传优化模糊控制[J].噪声与振动控制,2012,32(6):158-164.
[12]郭晓品.基于遗传算法的智能桁架结构模糊控制研究[D].邯郸:河北工程大学,2011.
[13]OHTORI Y, CHRISTENSON R E, ASCE A M, et al. Benchmark control problems for seismically excited nonlinear buildings[J]. Journal of Engineering Mechanics, 2004, 130(4): 366-385.
(责任编辑唐汉民梁碧芬)
Genetic algorithm optimized fuzzy control of nonlinear steel structure
ZHANG Yong-bing, LIANG Xing-yun, TANG Ying, CHEN Li-xing
(College of Civil and Architectural Engineering, Guangxi University, Nanning 530004, China)
Abstract:Membership functions and scaling factors of fuzzy logic controller wereoptimized by the genetic algorithm.The piezoelectric friction damper wasregarded as the control device, and an optimized fuzzy control algorithm was proposed to reduce the seismic response of nonlinear steel structures. Fuzzy controller based on dual inputs and single output, absolute value of interstory drifts and interstory velocities wereselected as input variables;voltages wereselected as output variables;triangular shapes wereselected as input and output variables of membership functions.Membership functions and scaling factors of fuzzy logic controller wereoptimized by thegenetic algorithm. A 3-story nonlinear steel structure wasanalyzed to simulate numerically the seismic responses under an optimized fuzzy logic controller.Numerical analysis results show that the fuzzy logic controllers optimized by genetic algorithm are effective in reduction of both acceleration and displacement responses of nonlinear steel structures.
Key words:steel structure; vibration control; fuzzy control; genetic algorithm
中图分类号:P315.966; TU352.11
文献标识码:A
文章编号:1001-7445(2016)01-0107-07
doi:10.13624/j.cnki.issn.1001-7445.2016.0107
通讯作者:张永兵(1979—),男,河南襄城人,广西大学副研究员,博士;E-mail:zhangyongbing@foxmail.com。
基金项目:广西自然科学基金资助项目(2013GXNSFBA019236);广西科技攻关计划项目(桂科攻12426001-5);“广西防灾减灾与工程安全重点实验室”系统性研究项目(2013ZDX10);广西大学科研项目(土科基-2012-03)
收稿日期:2015-11-12;
修订日期:2015-12-26
引文格式:张永兵,梁星云,唐滢,等.遗传算法优化的非线性钢结构模糊控制研究[J].广西大学学报(自然科学版),2016,41(1):107-113.
