新的混沌扩频序列抗多址性能的Simulink仿真
2016-02-29谢绍斌翁木云
万 康,谢绍斌,翁木云,周 双
(空军工程大学 信息与导航学院,陕西 西安 710077)
新的混沌扩频序列抗多址性能的Simulink仿真
万康,谢绍斌,翁木云,周双
(空军工程大学 信息与导航学院,陕西 西安710077)
摘要针对混沌扩频通信中提升混沌码性能的问题,通过重构Bernoulli映射相空间,得到一种改进的Bernoulli混沌映射,计算证明该映射具有弱结构特性,并在Simulink平台搭建了多用户混沌直接扩频通信系统的仿真模型,并与原Bernoulli混沌序列的抗多址性能做了比较。Simulink动态仿真结果表明,改进后的混沌扩频序列具有较好的抗多址干扰能力。
关键词混沌序列;扩频通信;重构;抗多址
Simulink Spread Spectrum Communication and Performance ofMulti-Access Based on New Chaotic Sequence
WAN Kang,XIE Shaobin,WENG Muyun,ZHOU Shuang
(School of Information and Navigation,Air Force Engineering University of PLA,Xi’an 710077,China)
AbstractA novel improved Bernoulli chaotic map is proposed according to reconstruction principle for better performance of chaotic spread spectrum sequence.The new map has a weak structure.Then the multi-user spread spectrum communication system is constructed by Simulink.Anti-multiple access capability of the chaotic sequence generated by the improved map and the Bernoulli map is analyzed.Simulation results show that new chaotic sequence has the better ability against noise and multiple access interference than the Bernoulli sequence.
Keywordschaotic sequence;spread spectrum communication;spread spectrum;anti-multiple access
混沌是确定系统内在随机性的表现,混沌系统对初始值的高度敏感性,不可能长期预测,混沌过程既非周期又不收敛[1]。传统扩频通信常用的伪随机序列有m序列、Gold序列等,但存在一定的缺点,如数目有限、线性复杂度低、保密性差等。混沌扩频序列具有随机性好、复杂度高、相关性好等优点,有望成为扩频通信系统中理想的扩频码[2-5]。
文献[6~8]均对混沌扩频通信系统做了仿真分析,主要是证明混沌扩频通信优于传统扩频通信,混沌扩频序列的产生使用的都是经典的混沌映射。本文对传统的Bernoulli映射进行重构,提出一种改进的Bernoulli映射,并在Simulink平台搭建混沌扩频通信系统,比较了改进前后系统的抗多址性能。
1重构Bernoulli映射
1.1 弱结构映射
对Bernoulli映射相空间结构拓扑压缩,再扩展到原有映射相空间,当压缩和扩展次数达到一定值时,系统具有弱结构特性。混沌系统的吸引子结构性越弱,产生的混沌序列随机性越好,系统保密性越高。基于Bernoulli映射的单边k段重构映射,可表示为

(1)
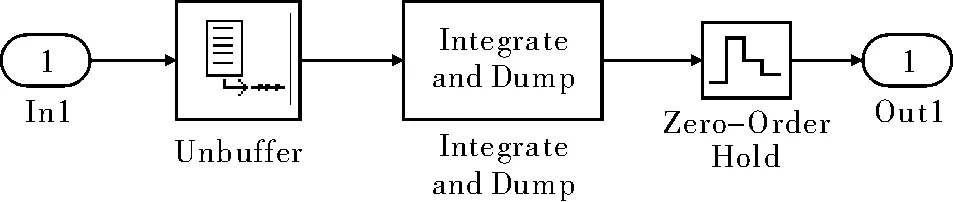
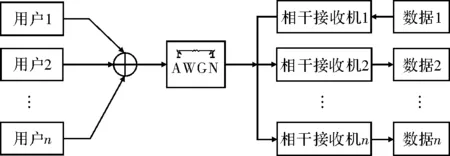
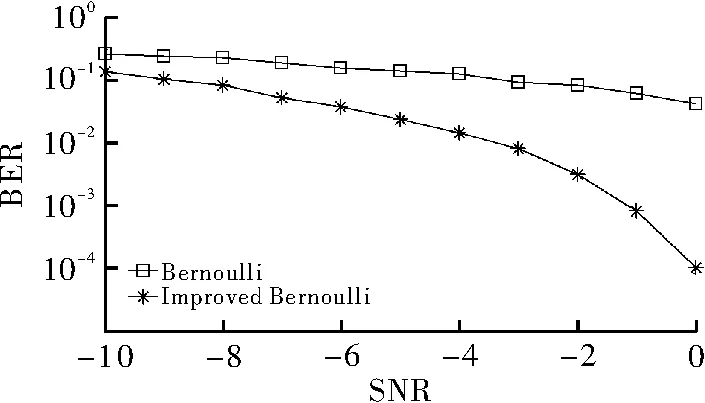
其中,k为系统段数;ξ为很小的正数。系统初始值-h/2 Lyapunov指数反映相空间中相近的两条轨迹发散或收敛的速率,正的Lyapunov指数越大,相空间轨迹发散速率越快。原Bernoulli系统最大Lyapunov指数由0.697增加到5.545,系统更复杂,具有弱结构特性。 图1 不同k值时系统相空间轨迹 扩频通信系统要求扩频序列具有良好的自相关性,而混沌系统相空间轨迹会影响混沌序列自相关性能,据APAS定理可知,若混沌系统相图关于坐标轴对称,则该系统产生的序列自相关性能好[10],归一化自相关函数有尖细的主峰,没有高的旁瓣。从图1中可看出,段数k=128时,映射相空间不关于坐标轴对称。现引入Tent映射控制序列符号,Tent映射可表示为 (2) 取a=0.5,b=(4-ξ),ξ与原映射中取值相同,初值L(0)取值范围为(-0.5,0.5),得到新的改进Bernoulli映射,结构为 (3) 段数k不同时系统相空间轨迹如图2所示,显然系统相空间轨迹呈轴对称结构。 图2 不同k值时符号受控系统相空间轨迹 2Simulink平台搭建混沌扩频通信系统 混沌直接序列扩频系统包括混沌扩频码产生、扩频、调制、解调、解扩、相关运算等[6],在实现混沌同步的前提下,Simulink平台上搭建的单用户系统模型如图3所示。 图3 单用户系统仿真图 要使用不同混沌系统时,改变Bernoulli模块中迭代表达式以及相关参数即可,比较方便。 2.2.1混沌序列发生器 混沌序列发生器结构如图4所示,用来产生扩频序列,扩频码速率为1/100 000,Unit Delay模块与Zero-Order Hold模块采样时间设置为10-5s。为充分利用Matlab的矩阵运算功能,提高数据处理效率和仿真速度,系统采用基于帧的处理方式,Buffer模块Output Buffer Size(积分抽样数)设置为1 000,其他设置为0,这样就保证了扩频码的仿真步长和信息码的仿真步长是一致的,均为1/100。 图4 混沌扩频序列发生器 2.2.2信息产生器 系统采用Random Integer Generator模块产生随机信号,作为用户发送的数字信息。若用户信息码速率为100 Hz,模块采样速率为1/100,则扩频增益β=1 000,模块输出为帧格式的二进制码元,每帧采样数为1,仿真步长为1×1/100。 2.2.3积分运算 积分运算子系统结构如图5所示。传送来的帧数据经过Unbuffer模块后解成序列形式,由积分模块积分,Integration Period设为1 000,Zero-Order Hold模块用来使每个输出的积分值保持在1/100 s,完成积分运算。 图5 积分运算子系统 3搭建多用户系统与仿真结果分析 当存在多个用户时,各个用户数据经扩频、调制后,在AWGN信道中叠加,在接收端分别实现相干解调,恢复出原信息。多用户混沌扩频通信系统可简化表示为如图6所示结构,基本原理与单用户系统相同。 图6 多用户混沌扩频通信系统框图 经过系统仿真,所设计的多用户混沌扩频通信系统解调结果如图7所示,恢复出的信息与原信息基本一致,只是存在时延,这是因为解调过程需要消耗一定的时间。说明该仿真系统能够正确解调出信息信号。 图7 多用户混沌扩频通信系统解调波形 改变AWGN模块信噪比,得出不同信噪比下系统的误码率。分别选择改进前后两种混沌系统来产生扩频序列,比较两种扩频序列的抗多址性能,选择用户数为3,结果如图8所示,改进后的混沌扩频序列抗多址干扰下的性能比原Bernoulli混沌序列更加优异。 图8 多址干扰下两种混沌通信系统BER比较 4结束语 针对提高混沌扩频码性能的问题,利用混沌相空间重构原理,对传统Bernoulli混沌映射相空间进行重构,得到一种新的改进Bernoulli混沌映射,在Simulink平台上构建多用户混沌直接序列扩频通信系统,分别使用两种混沌系统,比较多址干扰下系统的误码率,得出结论:改进Bernoulli映射产生的扩频序列抗多址性能得到了提升。 由于离散混沌系统的自同步问题尚未得到有效的解决,此系统并未实现收发两端混沌系统自同步,这是本仿真系统的不足之处,也是实现混沌数字通信的关键问题之一。 参考文献 [1]范一鸣,杨亚涛,许永涛.基于混沌序列的Simulink扩频通信仿真[J].计算机科学,2009,36(3):106-111. [2]LingCong,WuXiaofu,SunSonggeng.Ageneralefficientmethodforchaoticsignalestimation[J].IEEETransactionsonSignalProcessing,1999,47(5):1424-1428. [3]KohdaT,TsunedaA.Pseudonoisesequencesbychaoticnonlinearmapsandtheircorrelationproperties[J].IEICTransactionsonCommunication,1993(3):1811-1817. [4]ClareDMcgillem.Anovelmultiple-addressdigitalcommunicationsystemusingchaoticsignals[C].Chicago:ProceedingsofInternationalConferenceonCommunications,1992. [5]周志波,周童,王进祥.一种改进的多用户DCSK性能分析[J].西安电子科技大学学报:自然科学版,2009,36(4):730-735. [6]孙克辉,周家令,牟俊.多用户混沌扩频通信系统的设计与仿真[J].计算机仿真,2007,24(8):112-115. [7]SunYujuan,XuQunsan,WangZengfeng.PerformanceanalysisofdifferentspreadspectrumsequencecodeonAWGNchannel[J].WorldCongressonSoftwareEngineering,2009(30):506-508. [8]李杜娟,周子峰,吴成茂.基于正交混沌多用户混沌通信及其误码率[J].计算机应用,2014,34(4):963-968. [9]张志浩,姚宏,彭兴钊,等.飞机大迎角纵向机动稳定性及通向混沌的道路[J].空军工程大学学报:自然科学版,2014,15(3):15-19. [10]ChenBin.Assessmentandimprovementofauto-correlationperformanceofchaoticsequencesusingaphase-spacemethod[J].ScienceChinaInformationSciences,2011,54(12):2647-2659. 作者简介:万康(1991—),男,硕士研究生。研究方向:混沌数字通信。谢绍斌(1962—),男,副教授。研究方向:混沌雷达。 基金项目:国家自然科学基金资助项目(61202490);航空科学基金资助项目(20BZC15008) 收稿日期:2015- 05- 04 中图分类号TN914.42 文献标识码A 文章编号1007-7820(2016)01-075-04 doi:10.16180/j.cnki.issn1007-7820.2016.01.020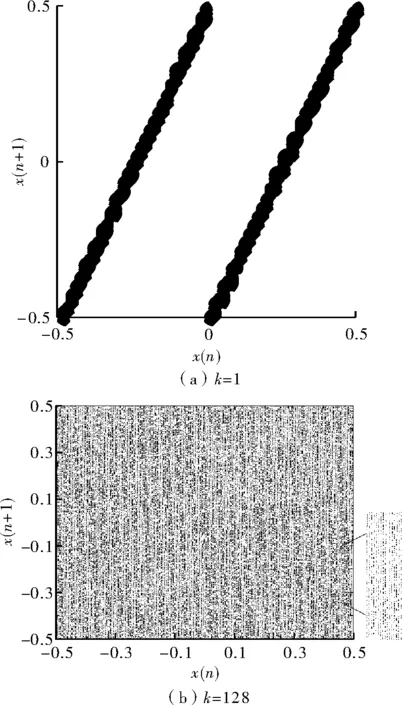
1.2 符号控制使相空间轨迹呈轴对称



2.1 单用户系统

2.2 模块与参数设定