基于非线性控制器设计的离散混沌系统同步方法

周　双,谢绍斌,万　康

(空军工程大学 信息与导航学院,陕西 西安　710077)

基于非线性控制器设计的离散混沌系统同步方法

周双,谢绍斌,万康

(空军工程大学 信息与导航学院,陕西 西安710077)

摘要在混沌通信系统工程化过程中,要求实时信号接收处理,实现收发两端系统的快速同步。为解决该问题,提出了以非线性控制器设计为基础的快速同步方案。针对离散混沌系统,采用Lyapunov函数同步法判定准则和反馈同步原理,合理设计了响应系统中的非线性控制器。仿真结果表明,同步误差可快速地稳定于零点,验证了该快速同步方法的正确性和有效性。

关键词Lyapunov函数法;离散混沌系统;非线性控制器;快速同步

A Synchronization Method for Discrete Chaotic Systems Based on Nonlinear Controller Design

ZHOU Shuang,XIE Shaobin,WAN Kang

(School of Information and Navigation,Air Force Engineering University,Xi’an 710077,China)

AbstractIn chaotic communication engineering,signals are required to be received and processed in real-time,thus the need for fast synchronization.A fast synchronization scheme based on nonlinear controller design is put forward.The nonlinear controller in response system is designed for discrete chaotic systems by adopting the Lyapunov function method and feedback synchronization principle.The simulation results show that synchronization error can quickly stabilize to near zero,verifying the correctness and effectiveness of the fast synchronization method.

KeywordsLyapunov function method;discrete chaotic system;nonlinear controller design;fast synchronization

自从1990年Pecora和Carrol发现了混沌的同步性,提出PC同步法,并且采用电路实现之后[1-2],混沌保密通信已成为信息安全领域的研究热点。混沌保密通信要求发送端和接收端的混沌系统同步,并提出了多种同步方法,如驱动-响应同步法[1]、主动-被动同步法[3]、线性耦合同步法[4-5]、反馈控制同步法[6-7]等。本文针对混沌通信工程化过程中的同步问题,提出了一种基于非线性控制器设计的离散混沌系统同步方法,同步误差可迅速稳定在零点附近,实现收发两端混沌系统的快速同步。

1混沌同步的判定准则

一般地,混沌系统的同步问题都转化为同步误差系统稳定性问题来研究,讨论同步误差系统的稳定性,采用经典的 Lyapunov函数法[8]。

Lyapunov函数法:对于同步误差系统en=yn-xn,如果存在关于误差en的函数V(en),满足:

(1)V(en)≥0,且只有在en=0时,V(en)=0;

(2)V(en+1)-V(en)≤0,且只有在en=0时V(en+1)-V(en)=0,

则同步误差系统en的极限趋于零,即

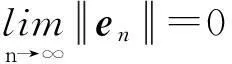
(1)

此时,同步误差系统en=yn-xn是渐进稳定的,即混沌系统可渐进地达到同步。

该混沌同步判定准则是混沌同步的充要条件,对于自治或非自治系统,甚至超混沌系统,只要能找到合适的Lyapunov函数,该判定准则都是适用的。

2非线性控制器设计的快速同步原理

2.1　反馈同步原理

反馈同步原理[9]利用驱动系统和响应系统的误差信号,通过施加反馈控制使响应系统跟踪驱动系统,从而实现混沌系统的同步。系统框图如图1所示。

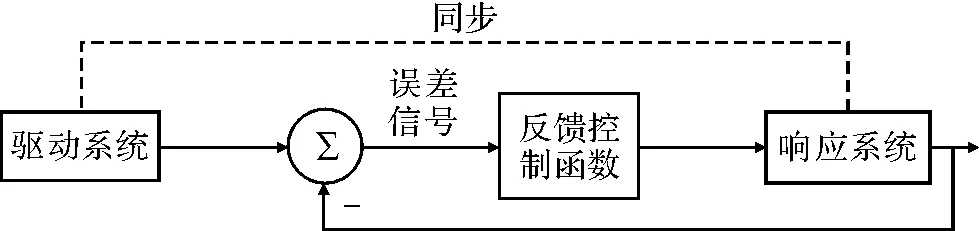
图1　反馈同步法系统框图

反馈同步原理分为参数反馈和状态变量反馈两种。参数反馈是指利用反馈的误差信号去调整系统的参数;状态变量反馈是指将反馈的误差信号直接加到响应系统的状态变量上去,不改变系统的参数[10]。在实际混沌通信工程中,并不希望混沌系统的参数发生改变,因此这里仅讨论状态变量反馈,其基本原理为:设n维自治离散迭代映射为驱动系统,由差分方程表示为

xn+1=G(xn)

(2)

其中,x=(x1,x2,…,xn)T为状态变量。

在响应系统中增加一个反馈控制函数

yn+1=F(yn)+U(xn,yn)

(3)

其中,y=(y1,y2,…,yn)T为状态变量;U(xn,yn)为反馈控制函数。选择合适的U(xn,yn),使得n→∞时,U(xn,yn)→0和yn→xn,即式(3)的解渐近跟踪式(2)的解,从而实现离散混沌系统的同步。

2.2　非线性控制器设计及证明

本文采用Lyapunov函数法判定准则,在反馈同步原理的基础上,提出了一种基于非线性控制器设计的离散混沌系统快速同步方法。驱动系统和响应系统分别如式(2)和式(3)。

将非线性控制器U分解为两项

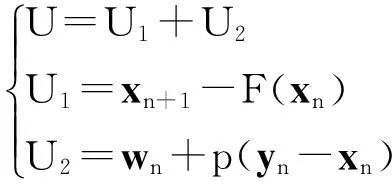
(4)

其中

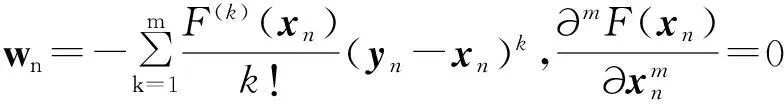
(5)

证明如下:

定义误差系统en=yn-xn,则

构造Lyapunov函数

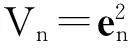
(6)

则对式(6)求差分方程可得

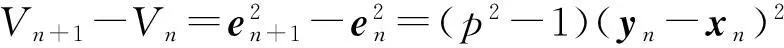
(7)

显然,Vn≥0,若满足

p2-1<0

(8)

3举例分析

3.1　Bernulli映射

Bernulli映射,中文又被称为伯努利映射,其是一种直线型映射。

Bernulli映射的数学表达式为

(9)

其中,μ为参数,当1<μ≤2时,系统达到混沌状态[11]。Bernulli映射分岔图如图2所示,Bernulli映射相图如图3所示。取值范围为xn∈[-0.5,0.5]。

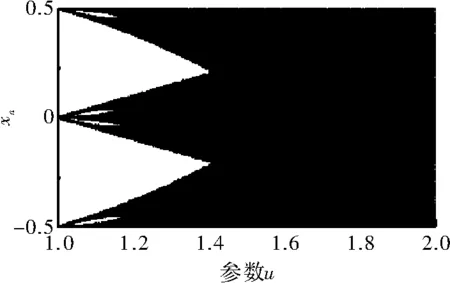
图2　Bernulli映射分岔图

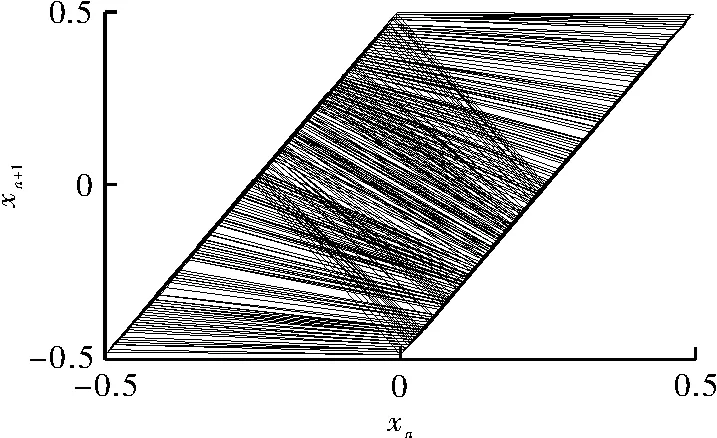
图3　Bernulli映射相图

3.2　Bernulli映射快速同步设计

设驱动系统如式(9),则设计响应系统为

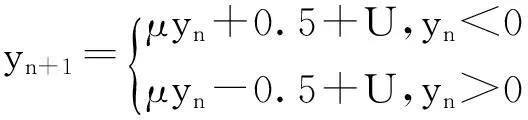
(10)

根据式(4)可知

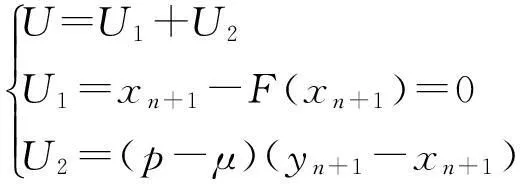
(11)

设误差系统为en=yn-xn,则

en+1=yn+1-xn+1=p(yn-xn)

(12)

3.3　Bernulli映射快速同步仿真分析

由于参数p与采样步数的关系难以用具体函数表示,所以本文采取数值仿真方法,优选参数p的大小。在数值仿真实验中,设p步长为0.01,且p∈(-1,1),则参数p与采样步数的关系如图4所示。根据图4优选参数p,可见当p=0时,采样步数最少,可实现离散混沌系统的快速同步。

图4　参数p与收敛步数关系图

选取参数p=0,假设驱动系统(9)和响应系统(10)的初始值分别为x0=-0.4,y0=0.4,此时同步误差系统的初始值为e0=0.8。图5为Bernulli映射同步误差曲线,可见当采样步数<3时,en已稳定在零点附近,实现了两个离散混沌系统的快速同步;图6为Bernulli映射同步过程模拟结果,从另一个角度验证了同步误差曲线的正确性。

图5　同步误差曲线

图6　驱动-响应波形图

4结束语

根据混沌通信工程的实际需要,在反馈同步原理的基础上,通过合理设计响应系统的非线性控制器,最终实现了离散混沌系统的快速同步。该快速同步方法的优点是收敛速度快,具有普遍性和稳定性,数值仿真验证了其正确性和有效性。在混沌通信工程中,一直存在混沌同步速度慢的问题,因此,该快速同步方法具有研究意义和实际应用意义。

参考文献

[1]PecoraLM,CarrollTL.Synchronizationinchaoticsystems[J].PhysicalReviewLetters,1990,64(8):821-824.

[2]CarrollTL,PecoraLM.Synchronizingchaoticcircuits[J].IEEETransactionsonCircuitsandSystems,1991,38(4):453-456.

[3]KocarevL,ParlitzU.Generalapproachforchaoticsynchronizationwithapplicationstocommunication[J].PhysicalReviewLetters,1995,74(6):5028-5031.

[4]RoyR.Experimentalsynchronizationofchaos[J].PhysicalReviewLetters,1994,72(13):2009-2012.

[5]SugawaraT.Observationofsynchronizationinlaserchaos[J].PhysicalReviewLetters,1994,72(22):3502-3505.

[6]JiangGP,TangKS.Aglobalsynchronizationcriterionforcoupledchaoticsystemsviaunidirectionallinearerrorfeedbackapproach[J].InternationalJournalofBifurcation&Chaos,2002,12(10):2239-2253.

[7]BuSL,WangSQ,YeHQ.Analgorithmbasedonvariablefeedbacktosynchronizechaoticandhyperchaoticsystems[J].PhysicalReviewD,2002,164(3):45-52.

[8]郑大钟.线性系统理论[M].北京:清华大学出版社,2002.

[9]王兴元.混沌系统的同步及在保密通信中的应用[M].北京:科学出版社,2012.

[10]徐瑞萍,高存臣.基于线性反馈控制的一类混沌系统的同步[J].中国海洋大学学报,2014,44(5):114-120.

[11]XieShaobin,HeZishu.Performanceofimprovedtentchaos-basedFMradarsignal[J].JournalofSystemsEngineeringandElectronics,2012,23(3):385-390.

[12]JovicB,UnsworthCP.Fastsynchronizationofchaoticmapsforsecurechaoticcommunications[J].ElectronicsLetters,2010,46(1):1-2.

[13]周双,谢绍斌.Lorenz系统单一耦合同步研究[J].空军工程大学学报:自然科学版,2015,16(5):80-84.

作者简介:周双(1990—),女,硕士研究生。研究方向:混沌同步及其在保密通信中的应用。谢绍斌(1962—),男,副教授,硕士生导师。研究方向:混沌信号理论及其应用。

基金项目:国家自然科学基金资助项目(61202490);航空科学基金资助项目(20BZC15008)

收稿日期:2015- 05- 11

中图分类号TN918

文献标识码A

文章编号1007-7820(2016)01-065-03

doi:10.16180/j.cnki.issn1007-7820.2016.01.017