30Cr2Ni4MoV低压转子加热过程的计算机模拟

王子荣　党淑娥　侯　微　刘海龙　秦尚武

(太原科技大学材料科学与工程学院，山西030024)



30Cr2Ni4MoV低压转子加热过程的计算机模拟

王子荣党淑娥侯微刘海龙秦尚武

(太原科技大学材料科学与工程学院，山西030024)

摘要：运用DEFORM-HT模块以30Cr2Ni4MoV低压转子为对象研究其升温过程中内部产生的温度场和热应力，获得了加热过程中低压转子截面几个关键位置处的升温曲线及热应力曲线，分析了最大截面上的温度分布以及温差对热应力的影响，得出了加热速度和保温时间与温差和热应力之间的关系。

关键词：30Cr2Ni4MoV钢；低压转子；温度场；热应力；计算机模拟

大型低压转子的热加工因其存在尺寸效应，所以在加热过程中会受到传热和导热等因素的影响。当加热工艺参数设定不当时，转子内部温度分布极不均匀，由此会引起转子内部不同部位在加热过程奥氏体化的程度不一样，即奥氏体晶粒大小分布不均匀，表层一定深度可能产生过热甚至过烧，而心部可能未发生完全奥氏体化，会导致高温状态下转子内部力学性能不均匀。尤其转子的半径方向会产生明显的温度差，这直接导致了热应力及组织应力的产生和累计，且温差越大，两者相互影响叠加后的综合应力就越大。当综合应力大于低压转子钢在设定温度下的屈服强度时就会造成工件变形，而大于抗拉强度则会造成断裂[1～5]。由于近年来计算机热处理模拟技术飞速发展产生了质的飞跃，融入了奥氏体化相变动力学和传热学等，所以不用实验也可以求出零件在热处理过程中任一时刻的温度场分布及热应力分布[6～11]。所以，若工件结构、加热介质和各种参数等详细而准确，就能实现实际生产过程的精准计算[12]。

本文运用DEFORM-HT模块以30Cr2Ni4MoV低压转子为对象研究其升温过程中内部产生的温度场和热应力。对加热过程转子截面几个关键位置处的升温曲线、最大截面上的温度分布、转子截面温差对热应力的影响进行了分析，从而根据模拟结果对转子加热过程所使用的工艺的合理性进行分析，为接下来改进加热工艺提供了理论指导。

1加热过程数值模型的建立

本文选取的低压转子见图1，加热工艺曲线如图2，以两者为基础进行温度场模拟，在此模拟基础上将其模拟结果作为输入参数进行瞬时应力-应变模拟。

图1　工件尺寸图

图2　热处理工艺曲线

汽轮机低压转子作为非常典型的轴对称工件，其在柱状坐标系下的温度场方程为：

(1)

式中，ρ为材料密度；Cp为材料比定压热容；T为工件瞬态温度；λ为材料导热系数；t为过程进行的时间；q′为相变潜热的热流密度；r、z分别为沿径向和轴向的坐标。

对瞬态温度场进行求解时，既需要相应的边界条件，也必须知道工件的初始条件。初始条件指的是所求解的非稳态传热问题在初始时刻区域中各点的温度，即工件装炉时的温度[13]。常用的换热边界条件为：

(2)

式中，H为边界综合换热系数；TC为环境温度，TW为低压转子与环境接触边界上温度。

2DEFORM-HT有限元模拟

2.1材料热物性参数的确定

低压转子钢30Cr2Ni4MoV导热系数λ与比热容Cp均为温度函数[14]，即

λ=33.44295+0.00224×T-1.57612E-5×T2

(马氏体，室温～700℃)

(3)

λ=118.23001-0.16649×T+745954E-5×T2

(奥氏体，800～1050℃)

(4)

Cp=0.5602-4.902×10-4T+1.407×10-6T2

(马氏体，室温～725℃)

(5)

Cp=2.746-3.350×10-3T+1.067×10-6T2

(奥氏体，770～900℃)

(6)

由上述公式可得出钢的比热容和导热系数，见表1和表2。

表1　30Cr2Ni4MoV钢不同温度的导热系数

表2　30Cr2Ni4MoV钢比热容随温度的变化

2.2模型的建立

图1所示的低压转子为典型轴对称阶梯轴，所以选取最大直径的1/4处为模拟对象，如图3所示。图3中P1、P2、P3分别表示工件径向不同距离处的节点，P4点表示转子棱边，P1-P3表示心部至表面的三等划分。

图3　工件网格划分和取点位置

2.3生产工艺和所需各类条件确定

大型锻件由于尺寸效应，加热过程中会产生很大的温差，所以采用阶梯缓慢加热的方式来减小表层和心部的温差。其加热工艺曲线如图2所示，即室温(本文选取20℃)时将转子装入炉中，以30℃/h的加热速度加热至300℃、保温10 h，再以17.5℃/h的加热速度升温到650℃、保温35 h，接下来以16℃/h的加热速度升温到890℃、保温75 h。

由于工件轴径比大，体积大，所以一般情况下利用井式电炉吊挂加热，工件的初始温度就是其刚装炉时的温度(本文选取20℃)。边界条件主要考虑工件和外界之间的热交换过程，本文换热边界条件采用第三类边界条件，主要是工件和加热炉气体的辐射与对流，换热系数经验公式如下所示：

h=2.56(TW-TC)0.25+4.6×10-8×

(7)

h=3.26(TW-TC)0.25+4.6×10-8×

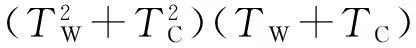
(8)

3模拟结果与分析

3.1温度场模拟结果及分析

本文运用DEFORM-HT模块，模拟可得低压转子径向截面从表层至轴心不同深度几个位置的升温曲线，见图4。从图4可知，加热过程中转子表面及棱边处温度升高较快，且接近原设定工艺，棱边和表层最大温差为34℃，但棱边达到指定温度要比表层早54 h，表明越接近设定工艺温度温升越慢，尤其当从885℃升高到890℃时耗时34 h，所以设定工艺时在温差允许范围内可适当提高温度上限以大大缩减加热时间。越靠近心部温度升高越慢，其升温过程已近似于一条斜线，其与设定工艺偏差较大，且越靠近表面处温差越大，转子表面与R/2处的温度差值最高值为216℃，但是R/2与轴心处温度差值最高值只有53℃，由此可知低压转子加热过程中同一径向截面不同位置的温度差值并非等距缩减，从工件表层到工件轴心处温度分布差异明显。

图4　转子最大截面处特殊部位的升温曲线

图5为转子加热过程中棱边、R/2、心部与表层的温差。可以看出，随着加热温度增大，转子径向温度差值飞速加大，且停止加热时其温度差值达到巅峰。保温时间越久转子径向温度差值渐渐变小，停止保温时温度差值变为最小。如当加热至650℃时，表面与心部温差达到最大值268℃，当650℃保温35 h后，温差减小至62℃，保温前后共减小温差达206℃。由此表明，阶梯式加热会有效减小大尺寸低压转子表面与心部温差，且加热过程阶梯越多，表面与心部温差越小。为了预测该转子在以上加热工艺条件下的热应力，以温度场模拟结果作为输入参数，对转子在加热过程中的瞬时应力分布进行简单分析，结果如图6所示。将图6与图5对比可以看出，热应力变化趋势与温差变化趋势相对一致，但不完全一致。转子棱边、表层、R/2、心部的最大热应力分别为15.3 MPa、21.6 MPa、23.6 MPa、23.4 MPa。棱边和表层的最大热应力发生在35 600 s处，由图4可知，该处是棱边和表层实际升温速率最大值的终了处，而R/2点极大热应力发生在159 000 s时，心部极大热应力发生在61 400 s时，两者均是实际加热速率极大值的终了处。由此可得，最大热应力并不是发生在最大温差处而是发生在最大升温速率终了处。由于低压转子一般要求其屈服应力为690 MPa～820 MPa，断裂应力约为830 MPa，如果不考虑其加热过程中的组织应力，单独来看热应力并不会致使其产生裂纹。

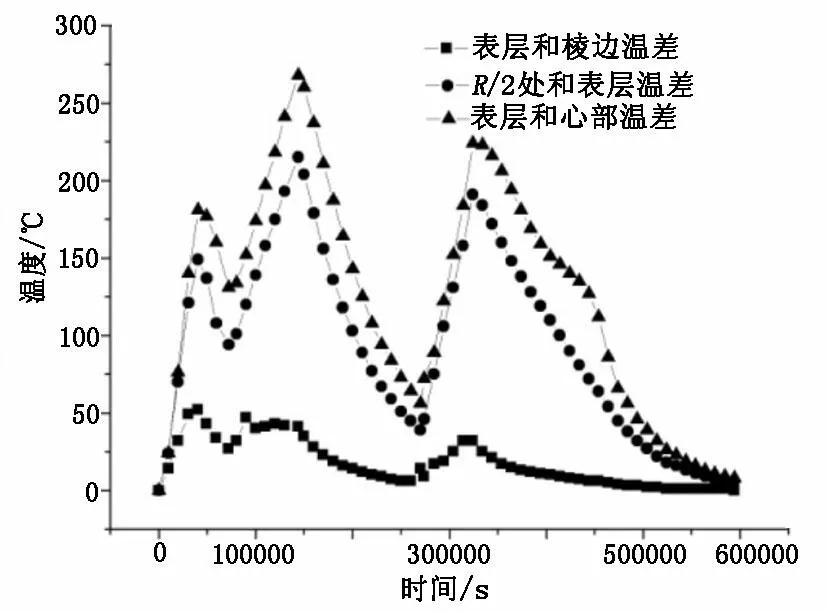
图5　工件升温过程中不同位置和表层之间温差

图6　转子轴向应力与时间变化的关系曲线

4结论

(1)低压转子最大截面处即使以0.29℃/min速度加热，也依然会造成表面与心部268℃的温差。所以在实际生产中一味降低加热速度并不能很好控制转子截面温度分布的均匀性。

(2)采用阶梯式加热可以有效地减小大截面低压转子的表面与心部温差，得到较均匀的温度分布。

(3)低压转子表面温度在升温过程中越接近设定温度，升温越缓慢，所以为了使工件尽快到达设定温度，可将炉温在误差允许范围内上调，这样可节省大量时间，缩短生产周期。

(4)低压转子最大截面上温差造成的热应力远远小于工件允许的变形及断裂应力，以给定的加热工艺曲线进行加热，其最大截面上的温差引起的热应力并不会对转子造成严重的变形及开裂。

参考文献

[1]孙福民,徐涛,王年臣,等.汽轮机热加工技术手册[M].哈尔滨:哈尔滨汽轮机厂有限责任公司, 2006.

[2]康大韬,叶国斌.大型锻件材料及热处理[M].北京:龙门书局,1998.

[3]雷雪,徐薇平,韩利战.低压转子加热过程模拟及工艺优化[D]. 上海交通大学，2009(9):48-51.

[4]张振国.大直径曲轴热处理后的残余应力分析[J].金属热处理，2005(08).

[5]罗利强.汽车轮毂轴承淬火残余应力的建模与仿真[D].浙江工业大学， 2010.

[6]Inoue T,A rim o to K. Implementation of program for simulating heat treatment processes and some results[J]. Industrial Heating, 1995(4): 41-45.

[7]William D Disler. Using on-line predictive computer modeling to optimize heat treat processing[J].Industrial Heating, 1996(9): 51-56.

[8]赵双群,林富生. 长期服役后高中压转子30Cr1Mo1V钢的性能研究[J]. 动力工程学报， 2012(05).

[9]朱伟，邓志成，申秀兰，等.核电汽轮低压转子强度有限元计算[J].发电设备，2014(01).

[10]李世键，孙明月，李殿中，孙嫘，孙海燕. 百万千瓦级核电转子中心压实过程的有限元模拟[J]. 热加工工艺， 2011(21).

[11]任武,张赵威,吴运新,李益华.多体列车车轴淬火温度场模拟和残余应力研究[J].热加工工艺，2014(18).

[12]吴淑珍，陈敬超，冯晶，等.钢铁淬火过程模拟的研究进展[J].材料导报，2008(6).

[13]匡琦，潘建生，叶建松.三维非线性有限元在热处理炉CAD中的应用研究[J].金属热处理，2001(11).

[14]王晓燕，顾剑锋，陈睿恺等.30Cr2Ni4MoV低压转子钢中不同微观组织的比热和导热系数的测定[J].金属热处理， 2011(4):1-3.

编辑杜青泉

Computer Simulation of Heating Process of

30Cr2Ni4MoV Low Pressure Rotor

Wang Zirong, Dang Shu′e, Hou Wei, Liu Hailong, Qin Shangwu

Abstract：By adopting DEFORM-HT module, the internally generated temperature field and thermal stress during the temperature rise period of 30Cr2Ni4MoV low pressure rotor have been studied. Then, the temperature rising curve and the thermal stress curve at several key points of cross section of rotor during the heating process have been obtained. Meanwhile, the distribution of temperature on the maximum cross section and the influence of thermal stress on temperature difference have been analyzed. Finally, the relationships between heating rate and holding time, temperature difference and thermal stress have been reached.

Key words：30Cr2Ni4MoV steel; low pressure rotor; temperature field; thermal stress; computer simulation

作者简介：王子荣(1990—)，男，硕士研究生，主要研究方向：大型锻造理论与新技术，热处理数值模拟。电话：15035123077，E-mail：244706565@qq.com

基金项目：国家自然科学基金资助项目(51275330)；山西省自然科学基金资助项目(2012011022-4)。

收稿日期：2015—09—14

中图分类号：O242.1

文献标志码：A