基于现代控制理论的减震刀杆设计与应用

赵永刚，宋培飞，王海平

（山西汾西重工有限责任公司，山西太原030027）

基于现代控制理论的减震刀杆设计与应用

赵永刚，宋培飞，王海平

（山西汾西重工有限责任公司，山西太原030027）

零件精加工过程中，颤振现象时有发生，为了避免加工过程中的颤振，提高零件加工质量，以镗刀杆为例，通过理论分析先确定影响镗削系统稳定性的因素，根据影响因素，设计了一种减震刀杆，通过改变刀杆的材料改变刀杆的静刚度和通过增大镗杆内部阻尼来提高刀杆动刚度进而实现减震目的，最终制造了减震刀杆，并通过切削试验验证，减震效果明显。

减震；静刚度；动刚度；颗粒阻尼

引言

在机械的切削加工（镗削、磨削和铣削）过程中都可能发生振动，尤其是在长悬臂刀杆的镗削孔、细长轴的车削、薄壁件的切削和螺纹的车削加工等[1]。机械加工过程中的振动使得工件加工表面质量恶化、粗糙度下降，这样不仅加速了刀具的磨损，还会引起机床连接件的松动和影响轴承的工作性能，使机床过早丧失精度等，因此，振动问题广泛地存在机械加工中，必须采用有效的技术措施来减轻或控制机械切削加工中的振动并阻止其扩散。

本方案通过理论分析得出影响机械加工中振动的因数[2]，并通过改变其影响要素设计了一种减震刀杆，最终通过现场切削验证，在零件精加工过程中控制颤振效果明显，提高了产品加工质量。

1 方案设计

本设计方案首先以镗刀镗削为例分析系统的质量（m）,弹性系数（K）和粘滞阻尼系数（f）对系统稳定性如何影响[3]。其次根据振动系统的影响因素来确定减震方案并设计减震刀具。

1.1 问题的理论分析

下面对镗削系统进行理论分析。

1.1.1 系统的分析

下面运用现代控制理论[4-5]对镗削系统进行理论分析：

与所研究的问题直接相关的就是镗刀杆，镗刀切削系统结构简图如图1所示，F（t）为切削力，X0（t）为镗刀刀尖处镗杆在切削力方向上的变形。

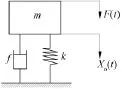
图1 镗刀切削系统物理模型

镗刀切削系统的物理模型如图1所示，m为镗刀系统运动的质量，f为镗刀系统粘滞阻尼系数，k为镗刀杆刚度。

根据下页图2的物理模型建立其数学模型为：

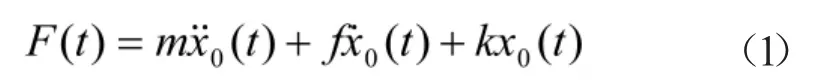
对式（1）进行拉普拉斯（LapLace）变换，并令初始条件为零，则：

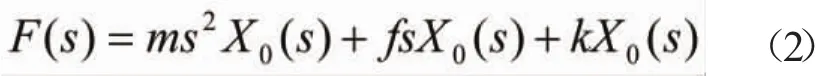
建立系统以名义去除量U0（s）为输入，以镗刀杆变形位移X0（s）为输出的传递函数为：

系统的特征方程为：

1.1.2 绘制系统的极坐标图

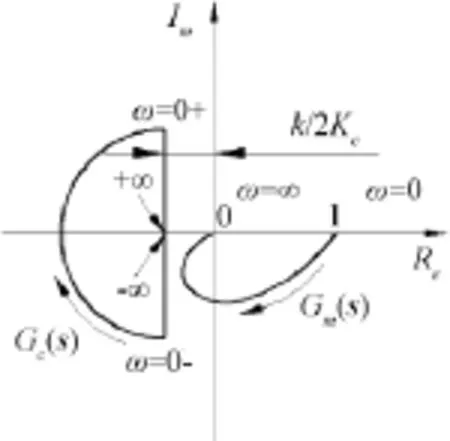
图2 系统的极坐标图

1.1.3 系统稳定的判断

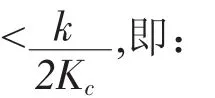
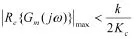
则系统稳定。

所以：

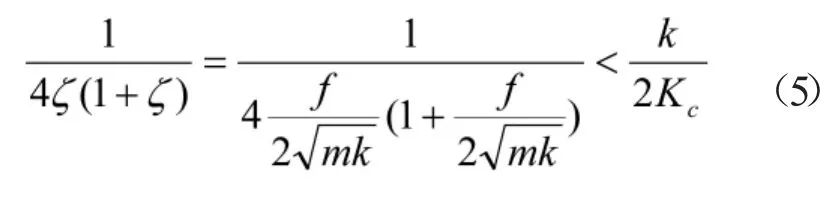
由此不等式可以看出，增大镗杆刚度k和粘滞阻尼系数f,或者降低切削系数Kc和质量m均有利于系统稳定。

1.2 减震刀具设计计算

通过上述分析，本方案中进一步探讨通过改变镗杆刚度K来达到减震目的，本减震刀杆同时改变镗杆的静刚度和动刚度[6,7]。

静刚度的改变主要是通过改变刀杆的材料（W6高速钢）同时淬火硬度63-66 HRC提高硬度。

动刚度的改变主要通过增大镗杆内部阻尼来提高刀杆动刚度进而实现减震目的，在接近刀头部分去除一部分用来提高振荡频率，在去除部分增加颗粒，通过其碰撞和摩擦吸收能量来提高动刚度。

图3 镗刀杆示意图

其中D为刀杆直径、d为空腔直径、l1为空腔长度、l和l1之和为悬出长度。

1.2.1 型腔直径的计算

为了计算方便，将图3简化为一悬臂梁（不包括刀头部分）如图4所示，如果在A点施加一个单位力F，那么在A点的刚度和挠度的关系为：

根据图4可知A点的挠度可以通过AB段和BC段挠度叠加来求出，即可先求B点的挠度Wb、B点的转角θB和A点相对于B点的位移量WAB,可知A点的挠度为：

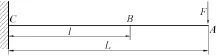
图4 镗刀杆简化受力图

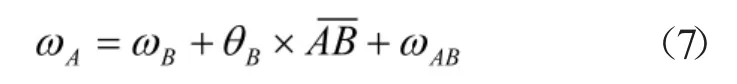
所以刀杆在A点的静刚度为：

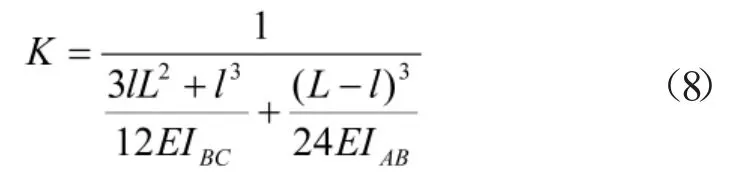
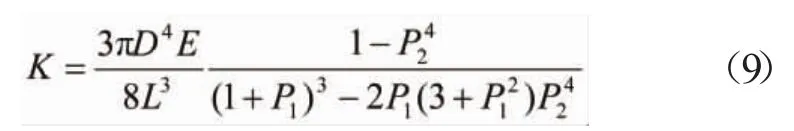
通过以上公式可知先列1-P42的相关数值来初步确定P2的取值，如下表1所示。

表1 空腔直径对A点静刚度的影响

由表1看出：在不大于0.7的范围内比较合理，考虑到空腔要有足够大的空间填充减震颗粒物质，所以P2应尽量取比较大的数值。初步确定为P2=0.7。

1.2.2 型腔长度的计算

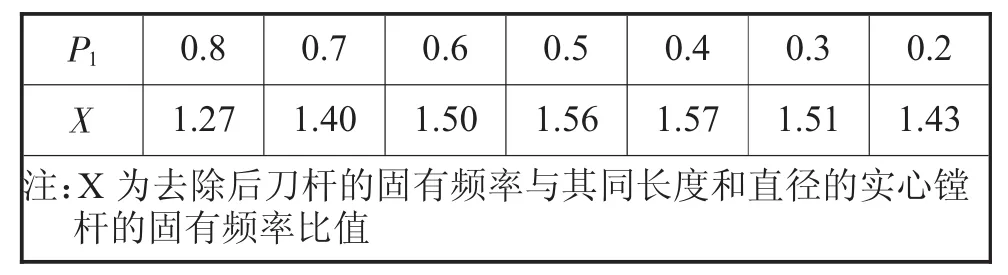
表2 空腔深度与固有频率的关系

根据上表中X值可以知道P1在0.6到0.3之间取值会有一个很好的固有频率。综合考虑刀杆的静刚度和抗弯强度，本文在这里初步确定P1=0.6。

1.2.3 刀杆阻尼材料的选则

阻尼的减震效果与空腔大小、填充比、颗粒种类等因素有关。但完善颗粒阻尼的理论还比较欠缺，只能通过现场镗削加工效果来验证减震刀杆，添加颗粒和粉的混合后减震效果是很明显的。本设计方案中选择铜球和铜粉进行配比作为阻尼颗粒[8,9]。

1.2.4 减震刀具的设计模型

根据某型产品的加工特点，首先确定镗刀杆的长度大于250mm,直径不小于25mm。

由于产品内台阶孔较多，每加工一道工步，就需对镗刀进行更换，更换后还要重新进行找正，为了提高加工零件的效率，本课题设计了可换式刀头，即一根减震刀杆配多种可换式减震刀头，一次装夹找正，即可完成零件的加工，如图5所示。

图5 减震刀杆模型图

2 试验验证及结果分析

由于实际条件的限制，无法进行实验室验证，本方案的验证只能选择加工实体进行实际镗加工验证。

减震镗刀具组合装配后悬壁长190 mm,普通镗杆在如此长悬臂的情况下，主轴转速上升到300 r/min就已经明显看到刀杆在颤振。

2.1 验证方案

选择零件进行镗削加工，加工后直观观察其表面粗糙度，通过设计实验方案进行2个项目的对比:一是进行非减震刀具与减震刀具的加工效果对比，如图6所示。二是同种材料的减震刀具选取不同切削参数后的效果对比，如图7所示。本实验方案通过改变切削参数（包括主轴转速、进给量、切削速度）来验证减震刀具的减震效果，主要通过提高主轴转速，其他切削参数暂设置为不变，详见下面对比图。

2.1.1 项目（详见图6）

2.1.2 项目（详见图7）

2.2 试验结果分析

通过上述试验数据，可以看出减震刀具的减震效果要明显优于非减震镗杆，在同为减震刀具的情况下，高速钢的减震效果要优于T8材料减震效果，因为高速钢材料的淬火硬度达到66HRC，而T8的淬火硬度为55HRC,高速钢材料减震刀具的静刚度要优于T8材料的静刚度。同样通过试验也能够验证，在转速不高的情况下，减震主要靠改变刀杆的静刚度，此时铜珠与内腔壁及铜珠与铜粉之间的运动主要是滑动摩擦来吸收能量。当转速不断提升，内腔的铜珠与铜粉及墙壁主要发生碰撞，此时减震颗粒之间的相互碰撞使铜珠与铜粉产生不可恢复的塑性变形，将颤振能量吸收，达到减振效果。

图6 非减震刀具和减震刀具对比图

图7 不同切削参数减震刀具对比图

[1]李红俊.复合结构减振镗杆设计[D],秦皇岛:燕山大学,2008:21-23.

[2]杨叔子.机械工程控制基础[M].武汉:华中科技大学出版社,2004.

[3]刘豹.现代控制理论[M].北京:机械工业出版社,1992.

[4]卢泽生，吴振顺，孙雅洲，等.控制理论及其应用[M].北京:高等教育出版社,2009.

[5]李友善.自动控制原理[M].北京:国防工业出版社,1983.

[6]许金凯.大长径比防振刀杆的研制与开发[D].长春:长春理工大学,2004:41-42.

[7]刘荣忠.减振刀杆的优化设计[J].振动与冲击,1993(4):29-35.

[8]戴德沛.阻尼技术的工程应用[M].北京:清华大学出版社,1991.

[9]刘棣华.粘弹阻尼减振降噪应用技术[M].北京:宇航出版社,1990.

（编辑：贾娟）

Design and App lication of Shock Absorber based on M odern Control Theory

Zhao Yonggang,Song Peifei,W ang Haiping
(Shanxi Fenxi Heavy Industries Co.,Ltd.,Taiyuan Shanxi030027)

In parts precisionmachining process,flutter phenomena occurs.In order to avoid flutter in the process,themachining quality of the parts should be improved.Taking boring bar as an example,through the theoretical analysis,the factors affecting the stability of the boring system is determined.According to the influencing factors,a shock absorber is designed.By changing the material,static stiffness is changed.By increasing internal damping,dynamic stiffness is improved and shock absorption is realized.Ultimately the shock absorber is created and verified by the cutting testswith obvious damping effect.

shock absorption;static stiffness;dynamic stiffness;particle damping

TP273

A

2095-0748(2016)23-0066-03

10.16525/j.cnki.14-1362/n.2016.23.31

2016-11-26

赵永刚（1981—），山西太原人，硕士研究生，工程师，研究方向：机械制造及自动化。