单服务器模型下双线性运算外包协议设计
2016-02-27王少辉刘梦青
王少辉,李 赫,刘梦青,肖 甫
(1.南京邮电大学 计算机学院,江苏 南京 210003;2.江苏省无线传感网高技术研究重点实验室,江苏 南京 210003)
单服务器模型下双线性运算外包协议设计
王少辉1,2,李 赫1,2,刘梦青1,2,肖 甫1,2
(1.南京邮电大学 计算机学院,江苏 南京 210003;2.江苏省无线传感网高技术研究重点实验室,江苏 南京 210003)
双线性对运算在密码学领域具有广泛的应用,但是双线性对运算也是此类密码协议中最耗计算资源的运算。目前解决该问题的方法之一是将复杂的运算外包给计算能力强大但不可信的服务器。对最近在双服务器模型下提出的双线性对运算外包协议的安全性进行了分析,分析结果表明如果资源受限设备发起的质询消息以明文的方式发送,则这些协议不能提供足够的安全性保障。并且在单服务器模型下提出了一个高效的可验证双线性对运算外包协议,即外包用户可以验证服务器回复消息的正确性。新协议中受限设备只需执行1个G1和G2中的标量加法和1个群GT中的模幂运算,执行效率要优于目前已提出的双线性对运算外包协议。
双线性对;云计算;安全外包;可验证性
1 概 述
2000年,Joux[1]发现椭圆曲线上双线性对可应用于密码算法的设计中,而Boneh和Franklin[2]利用双线性对提出了第一个适用的基于身份的加密方案。此后,双线性对运算成为密码学领域最常用的设计工具之一,其广泛应用于基于身份的密码系统的算法设计中。尽管众多密码学者提出不同的方法以提高双线性对运算的执行效率[3-4],但相比模幂运算,双线性对的计算成本仍然太高,以致不能应用在某些资源受限的设备中,如RFID、智能卡等。
随着云计算的快速发展,如何将耗资源运算,如模幂运算、双线性对运算,安全地外包给计算功能强大但不可信的服务器,已成为科学界密切关注的研究热点之一。在计算外包应用中,资源受限用户可以通过按次付费的方式,无限次使用外部的计算资源,从而减少企业用户在部署和维护硬件/软件方面的支出开销。
双线性对运算外包协议通常需要考虑如下的安全需求:
隐私性:该安全需求要求不可信服务器在参与运算外包的过程中,不能获得任何有关用户隐私数据的信息(如双线性对运算的输入或输出信息)。
可验证性:外包用户可以验证服务器返回结果的正确性,即一个诚信的云服务器返回的正确结果一定能通过用户的验证,并被用户接受;而恶意服务器返回的错误结果则不能通过用户的验证。
服务器的数量:在单服务器模型中,只允许一个不可信服务器参与运算外包协议;而双服务器模型则意味着用户将运算外包给两个相互独立的服务器,并假设这两个服务器独立运作,不会合谋以获得额外的秘密信息。
针对具体的密码学运算,密码学者已经提出了众多运算外包协议[5-7],同时也提出了一些通用的安全运算外包协议构造[8-9]。具体到双线性对运算,2005年,Girault和Lefranc[10]提出了服务器辅助验证的概念,第一次对基于双线性对密码方案的安全外包算法进行了研究。他们将双线性对运算的输入进行盲化,从而实现了无条件的隐私性安全保障。Mames等[11]首次提出了可验证的双线性对运算外包协议,他们通过让一台服务器计算两组可比较的结果来检查服务器返回数据的正确性。Kang等[12]对文献[11]的结果进行改进,提出了一种更高效的方案。但是,这些方案的计算效率仍然比较低,并不能适用在资源受限的设备中。
Canard等在文献[13]中提出了一种更高效的可验证双线性对运算外包协议。当双线性对的输入可公开时,该协议只需要2个群G1和G2中的标量乘法运算和1个群GT下的模幂运算。Guillevic等[14]提出了两种满足隐私性的高效双线性对运算外包协议。在单服务器模式下,新协议的执行效率要优于以往所有协议,但该协议不满足可验证性。针对双服务器模型,Chen等[15]提出了一种安全的双线性对运算外包协议,该协议的显著特点是资源受限设备不需要进行任何耗资源操作,如群G1上的标量乘法运算或GT上的模幂运算。最近,Tian等[16]在双服务器模型下,提出了两种新的计算外包算法以优化文献[15]算法的效率。
文中首先回顾了在双服务器模型下最近新提出的一些双线性对运算外包协议[15-16]的安全性。在双服务器模型下,通常都假设两个服务器中至多存在一个恶意的服务器。如果资源受限设备发送的质询消息是明文发送,则文献[15-16]中所提方案并不能抵御攻击者或恶意服务器所发起的被动攻击,其可以以很高的概率推断出双线性对运算的输入或输出。接着在单服务器模型下提出了一种高效的可验证双线性对运算外包协议,新方案只需1个群G1和G2中的标量乘法运算和1个群GT中的模幂运算。
2 基础知识
2.1 双线性对
设加法循环群G1、G2和乘法循环群GT具有相同的大素数阶q,g1、g2分别为群G1和G2的生成元,双线性对运算e:G1×G2→GT满足3个性质:
(2)非退化性:存在R∈G1,Q∈G2,并且有e(R,Q)≠1;
(3)可计算性:对所有R∈G1,Q∈G2,存在有效算法计算e(R,Q)。
2.2 安全双线性对运算外包协议
通常一种安全的双线性对运算外包协议由计算资源受限的外包用户T和计算资源强大的外包服务器组成,按照参与服务器的数目,可以分为单服务器运算外包协议和双服务器运算外包协议。图1给出了单服务器下的双线性对运算外包协议的执行过程。此时,用户T为了计算双线性对e(A,B)的值,首先向服务器发起质询消息(QueryMessages);然后服务器对用户的质询做出响应(ResponseMessages);用户最终将推导得到双线性对e(A,B)的值。
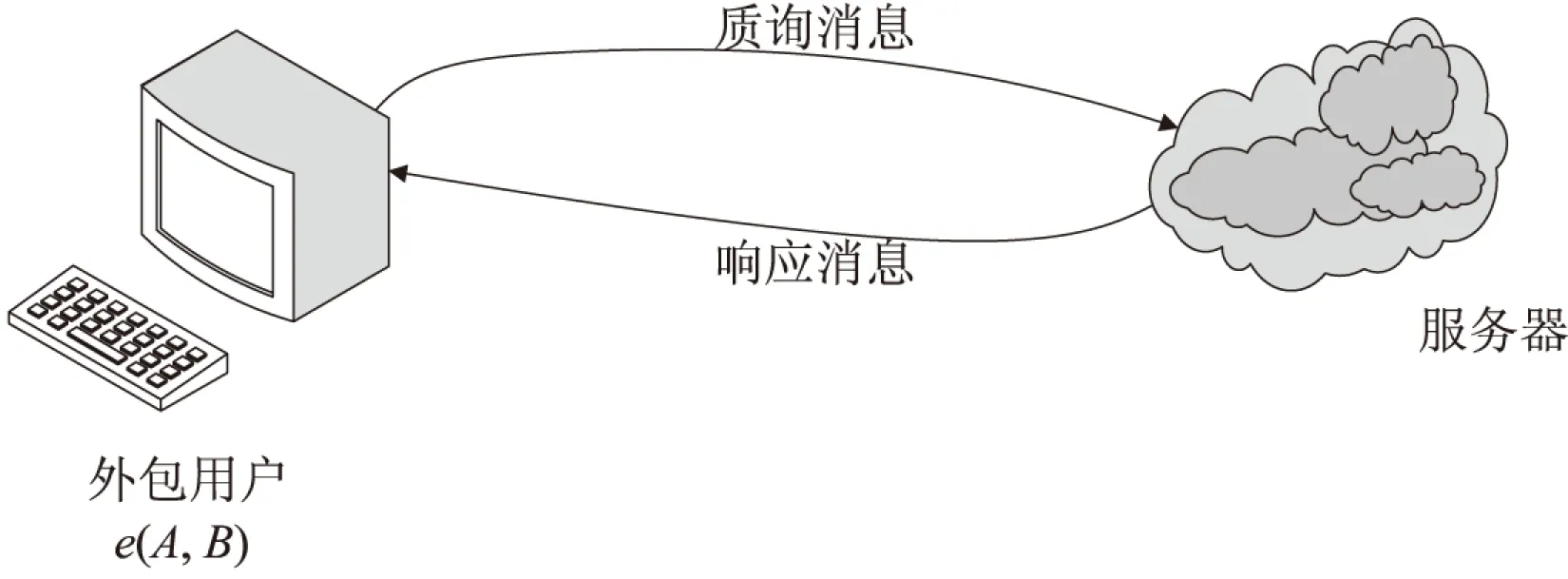
图1 单服务器模型下的运算外包过程
Mames等[11]指出一个安全的单服务器双线性对运算外包协议应提供完备性、可验证性和隐私性这三种安全需求:
(1)完整性:当外包用户和一个诚实的服务器交互执行协议后,用户T将以不可忽略的概率优势计算得到e(A,B)。
(2)隐私性:一个不可信服务器不能通过协议的交互获得任何关于双线性对输入A和B,或者输出e(A,B)的信息。将外包协议执行过程中,服务器所接收到的消息记做View(A,B),隐私性也就是说,对于任何恶意服务器,都存在一个模拟器S,对于任何输入A和B,模拟器S的输出和服务器接收的消息View(A,B)计算不可区分。
(3)可验证性:外包用户T能以不可忽略的概率优势检测到不可信服务器的欺骗行为。即,对任意的双线性对输入A和B,对于不可信服务器的错误响应消息,用户T能以不可忽略的概率优势发现错误,并输出错误结果⊥。
双服务器模型下的双线性对运算外包协议执行过程如图2所示。此时外包用户将分别向两个服务器发起质询消息,并利用接收到的两组应答消息计算得到e(A,B)的值。双服务器模型要求两个服务器至少有一个是诚实服务器,并且两个服务器彼此独立运行,不会合谋破坏协议的安全性,其安全需求与单服务器模型下的外包协议类似,这里不再赘述。

图2 双服务器模型下的运算外包过程
3 方案的安全分析
最近,Chen等[15]在双服务器模型下,提出了一种高效的双线性对运算外包协议Pair。与以往的算法相比,Pair协议的显著特性是外包用户T只需要进行群G1和G2中的点加运算和群GT中的乘法运算,而不需要进行任何耗资源运算,如标量乘法运算和模幂运算。而在2015年AsiaCCS国际大会上,Tian等[16]进一步改进了Chen等的方案,提出了两种新的双服务器模型下的双线性对运算外包协议。
因为外包用户T通常是一些资源受限的设备,如智能卡片、RFID标签或传感器节点,所以通常在外包用户和服务器之间创建安全信道是不可行的。如果外包用户T发起的质询消息以明文的方式发送给服务器,那么文献[15-16]所提方案将不能提供任何的安全保障,因为攻击者通过被动的侦听信道便可以以很高的概率优势推断出双向性对运算的输入A,B以及输出e(A,B)。
下面以Pair协议为例,说明上面提到的三种双线性对运算外包协议存在的安全缺陷。

对于A∈G1,B∈G2,为了安全外包运算e(A,B),Pair协议将执行以下操作:
(1)用户T运行Rand算法得到三个六元组:(Xi,Yi,xiXi,yiXi,yiYi,e(Xi,Yi)xi+yi-xiyi),i=1,2,3。
(2)用户T按照随机顺序向服务器1发起以下质询:
S1(A+x1X1,B+y1Y1)→e(A+x1X1,B+y1Y1)=α1
S1(x2X2,y2Y2)→e(x2X2,y2Y2)
S1(x3X3,y3Y3)→e(x3X3,y3Y3)
其中,S1(ι1,ι2)→e(ι1,ι2)表示用户T发送双线性对的输入(ι1,ι2)给服务器1,而服务器1返回响应结果e(ι1,ι2)。
(3)用户T按照随机顺序向服务器2发起以下质询:
S2(A+X1,y1Y1)→e(A+X1,y1Y1)=α2
S2(x1X1,B+Y1)→e(x1X1,B+Y1)=α3
S2(x2X2,y2Y2)→e(x2X2,y2Y2)
S2(x3X3,y3Y3)→e(x3X3,y3Y3)
(4)用户T通过检验两个服务器是否返回不同的e(x2X2,y2Y2)和e(x3X3,y3Y3)的值来验证两个服务器中是否存在恶意服务器。如果不相等则验证失败,T输出“错误”;否则e(A,B)可以通过如下方式计算得到:
安全分析如下:
假设用户T发送给服务器1和服务器2的质询消息都为明文,一个被动攻击者可以通过窃听信道,收集到双线性对运算的7对输入和响应的回复消息。如果两个服务器都诚实地执行Pair协议,攻击者通过比较响应消息,可以丢弃双线性对e(x2X2,y2Y2)和e(x3X3,y3Y3)。
此时攻击者手中拥有三组质询—响应消息组:((β1,β2)→α1), ((γ1,θ1)→α2), ((γ2,θ2)→α3)。这样攻击者可以以0.5的概率推导出e(A,B)的值,因为下面的两个等式至少有一个成立:
e(A,B)=e(β1-γ1,β2-θ2)
e(A,B)=e(β1-γ2,β2-θ1)
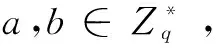
4 单服务器模型下外包协议的设计
本节首先在单服务器模型下,提出了一种新的双线性对运算外包协议,然后给出协议的安全性分析以及和其他协议的性能比较。
4.1 新方案设计
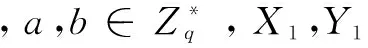
协议的输入是A∈G1,B∈G2,输出是e(A,B),其中要求输入A,B满足隐私性。新单服务器下的双线性对运算外包协议执行如下:
(1)用户T调用Rand算法得到一个新的七元组:(a,b,-X1,-Y1,aX1,bY1,e(X1,Y1)-ab)。
(2)用户T向服务器发起以下随机查询:
S(A+aX1,B+bY1)→e(A+aX1,B+bY1)=α1
S(bA,aB)→e(bA,aB)=α2
S(-X1,aB)→e(-X1,aB)=α3
S(bA,-Y1)→e(bA,-Y1)=α4
(3)用户T检查如下公式是否成立:
α2=(α1α3α4e(X1,Y1)-ab)ab
若成立,则计算并得到双线对e(A,B)的值为:
e(A,B)=α1α3α4e(X1,Y1)-ab
否则,拒绝服务器端返回的结果,并输出“错误”。
4.2 性能比较和安全性分析
(1)性能比较。
Canard等在文献[13]中针对双线性对e(A,B)的输入A和B可公开的应用,提出了一种高效的双线性对运算外包协议,同时为了获得输入信息的隐私性,他们还提出了一般的通用转换方法。Canard等所提方案是目前单服务器模型下效率最优的双线性对运算外包协议,表1中给出了文中新提出的外包协议和Canard等所提方案中外包用户和服务器的性能比较。

表1 计算开销比较
这里只统计在线运算量。如表1所示,m1,m2分别表示群G1和G2中的标量乘法运算,而eT代表群GT中的模幂运算,这两种运算比群G1的点加运算或GT的点乘运算要耗费更多的资源。通过比较可以看出,文中提出的新算法中,外包用户需要1个群G1和G2中的标量乘法运算,和1个群GT中的模幂运算,远少于文献[13]中外包用户的计算量;而两种协议中服务器端的计算量相当,都需要计算4个双线性对运算,这里用PT表示。
(2)安全分析。
类似文献[11-12]中协议的安全性论证,通过如下定理证明新协议满足运算外包协议的安全需求。
定理1:新提出的双线性对运算外包协议是一种满足隐私性的安全可验证的运算外包协议,即新协议满足完备性、保密性和可验证性。
证明:
完备性:容易验证下列公式一定成立:
α1α3α4e(X1,Y1)-ab=e(A+aX1,B+
bY1)e(-X1,aB)e(bA,-Y1)e(X1,Y1)-ab=
e(A,B)e(A,Y1)be(X1,B)ae(X1,Y1)abe(A,
Y1)-be(X1,B)-ae(X1,Y1)-ab=e(A,B)
并且有:
α2=e(bA,aB)=e(A,B)ab
隐私性:从协议的设计可以看到,服务器所接收到的质询消息均是来自群G1和G2中随机独立分布的点。因此,模拟器S只需运行生成群G1和G2中随机点,此时,模拟器的输出和服务器接收到的消息分布计算不可区分。
可验证性:如果α2≠e(A,B)ab,则下面的值在群GT中几乎均匀地分布:
(1)
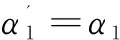
假设X1和Y1分别是G1和G2的生成元,并且A=xX1,B=yY1。对于x,y,u,v,w,z∈Zq,记U=A+aX1=uX1,V=B+bY1=vY1,W=bA=wX1和Z=aB=zY1。显然下列等式一定成立:
u=x+a,v=y+b,w=bx,z=ay
并且存在β1,β2,β3,β4∈Zq,有如下等式成立:
α1=e(A+aX1,B+bY1)e(X1,Y1)β1
α2=e(A,B)abe(X1,Y1)β2
α3=e(X1,B)-ae(X1,Y1)β3
α4=e(A,Y1)-be(X1,Y1)β4
显然当且仅当β2=0时,α2=e(A,B)ab。下面将说明当β2≠0时,用户T将以不可忽略的概率输出“错误”。由式(1)可以得到:

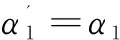
β1=β2(ab)-1-β3-β4modq
5 结束语
文中首先对最近提出的双服务器模型下的双线性对运算外包协议的安全性进行了分析,分析结果表明如果应用中不存在安全信道,这些方案并不能提供足够的安全性保证。作为被动的攻击者,可以以较大的概率优势推测得到用户所计算的双线性对运算的输入和输出参数。同时,针对单服务器模型,提出了一种高效的可验证的安全双线性对运算外包协议,在解决双线性对计算问题的同时,也保证了服务端返回结果的可验证性,以使外包用户可以放心地将自身的运算外包给云服务器完成。新方案只需要1个群G1和G2的标量加法运算,和1个群GT下的模幂运算。经过比较分析,可以看出新协议的执行效率要明显优于目前已有的方案。
为了提供可验证性,认为在单服务器模型下设计双线性对运算外包协议不可避免地要用到模幂运算,而模幂运算是除双线性对运算外最耗费资源的密码学运算。如何在单服务器模型和双服务器模型下设计更为高效的安全双线性对运算外包协议,将是下一步重点考虑的研究工作。
[1]JouxA.AoneroundprotocolfortripartiteDiffie-Hellman[C]//Internationalalgorithmicnumbertheorysymposium.[s.l.]:[s.n.],2006:385-393.
[2]BonehD,FranklinM.Identity-basedencryptionfromtheWeilpairing[C]//Annualinternationalcryptologyconference.Berlin:Springer,2001:213-229.
[3]BarretoP,GalbraithS,OheigeartaighC,etal.EfficientpairingcomputationonsupersingularAbelianvarieties[J].Designs,CodesandCryptography,2007,42(3):239-271.
[4]BarretoP,NaehrigM.Pairing-friendlyellipticcurvesofprimeorder[C]//Internationalworkshoponselectedareasincryptography.Berlin:Springer,2005.
[5]MatsumotoT,KatoK,ImaiH.Speedingupsecretcomputationswithinsecureauxiliarydevices[C]//Conferenceonthetheoryandapplicationofcryptography.NewYork:Springer,1988.
[6]ChaumD,PedersenT.Walletdatabaseswithobservers[C]//Annualinternationalcryptologyconference.Berlin:Springer,1992.
[7]LimCH,LeePJ.Server(prover/signer)-aidedverificationofidentityproofsandsignatures[C]//Internationalconferenceonthetheoryandapplicationsofcryptographictechniques.Berlin:Springer,1995.
[8]YaoAC.Protocolsforsecurecomputations[C]//23rdannualsymposiumonfoundationsofcomputerscience.[s.l.]:[s.n.],1982.
[9]CanardS,CoiselI,DevigneJ,etal.Towardgenericmethodforserver-aidedcryptography[C]//Internationalconferenceoninformationandcommunicationssecurity.[s.l.]:SpringerInternationalPublishing,2013.
[10]GiraultM,LefrancD.Server-aidedverification:theoryandpractice[C]//Internationalconferenceonthetheoryandapplicationofcryptologyandinformationsecurity.Berlin:Springer,2005.
[11]Chevallier-MamesB,CoronJS,McCullaghN,etal.Securedelegationofelliptic-curvepairing[C]//Internationalconferenceonsmartcardresearchandadvancedapplications.Berlin:Springer,2010.
[12]KangB,LeeM,ParkJ.Efficientdelegationofpairingcomputation[R].[s.l.]:[s.n.],2005.
[13]CanardS,DevigneJ,SandersO.Delegatingapairingcanbebothsecureandefficient[C]//Internationalconferenceonappliedcryptographyandnetworksecurity.[s.l.]:SpringerInternationalPublishing,2014.
[14]GuillevicA,VergnaudD.Algorithmsforoutsourcingpairingcomputation[C]//Internationalconferenceonsmartcardresearchandadvancedapplications.[s.l.]:SpringerInternationalPublishing,2014.
[15]ChenXiaofeng,SusiloW,LiJin,etal.Efficientalgorithmsforsecureoutsourcingofbilinearpairings[J].TheoreticalComputerScience,2015,562:112-121.
[16]TianHaibo,ZhangFangguo,RenKui.Securebilinearpairingoutsourcingmademoreefficientandflexible[C]//Proceedingsofthe10thACMsymposiumoninformation,computerandcommunicationssecurity.[s.l.]:ACM,2015.
Design of Efficient Outsourcing Protocol of Bilinear Pairings for a Single Server
WANG Shao-hui1,2,LI He1,2,LIU Meng-qing1,2,XIAO Fu1,2
(1.College of Computer,Nanjing University of Posts and Telecommunications,Nanjing 210003,China; 2.Key Laboratory of Jiangsu High Technology Research for Wireless Sensor Networks,Nanjing 210003,China)
Bilinear pairing operation has been widely applied in cryptography field,but the computation of bilinear pairings has been considered the most expensive operation in pairing-based cryptographic protocol.One of the ways to solve this problem now is to outsource expensive computation to untrusted but powerful servers.The security of some recently proposed pairing delegation algorithms are analyzed in the two-server assumption model,and it is found that if the query messages sent by the source-constrained devices are plaintext,these protocols cannot provide enough security guarantee.Also an efficient verifiable secret pairing outsourcing protocol is put forward in the single server assumption model,and the protocol enables the limited device to verify the value received from the server with one scalar addition inG1andG2,andoneexponentiationinGT,whichismuchmoreefficientthantheexistingprotocols.
bilinear pairing;cloud computing;secure outsourcing;verifiability
2016-01-29
2016-05-18
时间:2016-10-24
国家自然科学基金资助项目(61373006,61373139);江苏省科技支撑计划基金项目(61003236);南京邮电大学校科研项目(NY214064,NY213036)
王少辉(1977-),男,博士,副教授,研究方向为信息安全、密码学;李 赫(1993-),男,硕士研究生,研究方向为P2P网络安全。
http://www.cnki.net/kcms/detail/61.1450.TP.20161024.1117.074.html
TP
A
1673-629X(2016)11-0116-05
10.3969/j.issn.1673-629X.2016.11.026
