PID控制器采用双线性变换法离散存在的问题分析
2016-02-26赵冬玉王利伟赵伟东
赵冬玉 王利伟 赵伟东

【摘 要】本文给出了PID控制器传递函数的参数及被控对象的函数,然后采用双线性变换法设计数字PID控制器,并针对被控对象分析双线性变换法离散化后的控制效果,发现双线性变换设计法不适宜于数字PID控制器的设计。最后分析了PID控制器不能采用双线性变换法离散的原因。
【关键词】PID控制器;双线性变换法;微分环节
0 引言
PID控制器问世至今已有近70年历史,它以其结构简单、稳定性好、工作可靠、调整方便而成为工业控制的主要技术之一。当被控对象的结构和参数不能完全掌握,或得不到精确的数学模型时,控制理论的其它技术难以采用时,系统控制器的结构和参数必须依据经验和现场调试来确定,这时应用PID控制技术最为方便。即当我们不完全了解一个系统和被控对象﹐或不能通过有效的测量手段来获得系统参数时,最适合用PID控制技术。
随着数字化的发展,对PID控制器的各种离散方法的层出不穷,各种离散方法都有本身的优点和局限性,本文就其采用双线性变换法离散存在的问题进行分析,从而得出PID控制器不能采用双线性变换法离散的原因所在。
1 PID控制器及双线性变换法
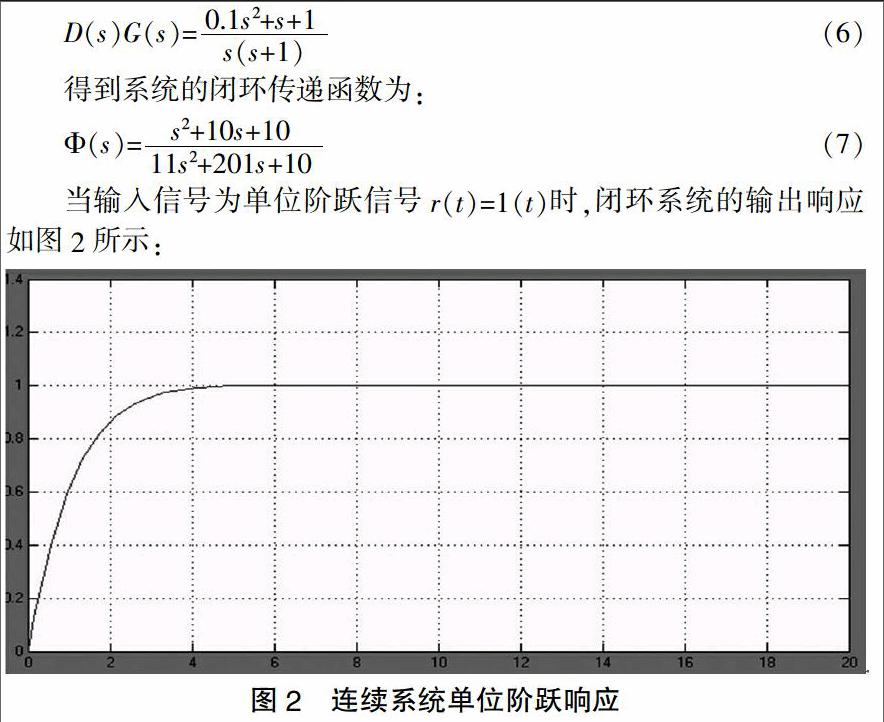
该系统是一个I型系统,所以当输入为阶跃信号时,系统的稳态误差为0。由于PID 控制器中的积分环节I为系统提供一个位于原点的开环极点,提高系统型别保证系统稳定性。系统的动态性能良好,超调量σ%=0,调节时间ts=3.4s,上升时间tr=2.9s。
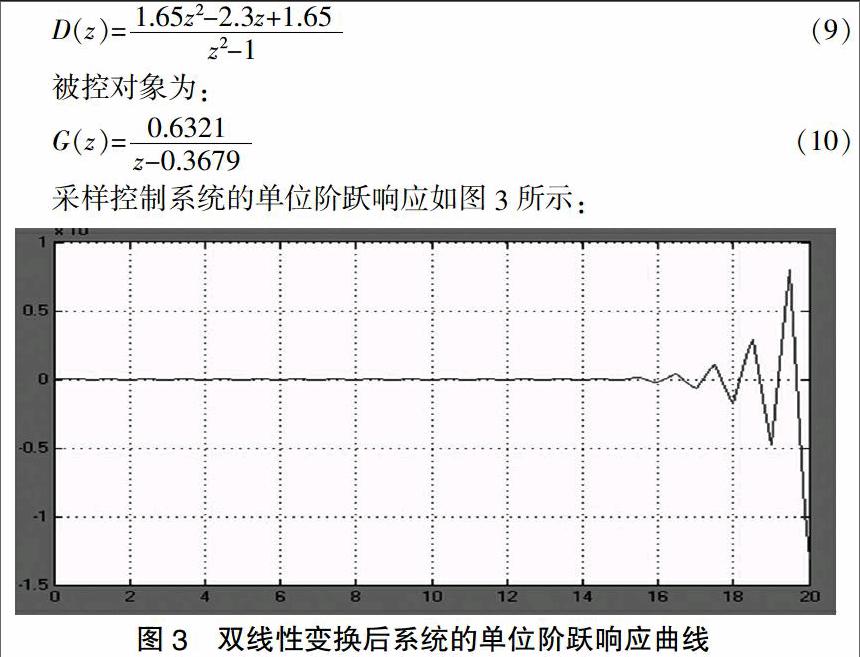
可见采用双线性变换后,系统在很长时间内输出量很小,系统输出经一段时间后上下扰动加剧,并随着时间的延长,这种扰动的幅值不断扩大,严重破坏系统的性能,最后使系统崩溃。
3 PID控制器采用双线性变换法离散存在的问题分析
PID控制器实际上是由比例环节P,积分环节I,微分环节D叠加构成。那么究竟是其中哪一个环节使得输出产生如此剧烈的振荡,显然,比例环节不可能使系统随时间发散,它只会改变系统增益。因此,分别只采用单个积分或微分环节进行离散化后观察系统性能,以此找出产生振荡的原因。
当只采用积分环节时,D(s)=,D(z)=,G(z)=。系统的单位阶跃响应曲线如图4所示:
从图4及5可以看出,当只采用积分环节时系统的稳态误差为0,超调量σ%=31,调节时间ts=11.6s,上升时间tr=1.3s。积分环节只改变了系统的动态性能,使系统动态性能变差,但没有改变系统的稳态性能。而微分环节的控制器却使整个闭环系统的稳态性能,动态性能变得极差。系统的输出经过一段时间后扰动幅值不断加剧,最终会使整个系统完全崩溃。
即σ2+ω2<1。这相应于Z平面单位圆内部。因此,双线性变换将S平面上整个左半平面映射到Z平面上以原点为圆心的单位圆内部(这是Z平面上的稳定区)。同理可知双线性变换将S右半平面映射到单位圆外,将S平面上的虚轴映射到单位圆上(映射关系如图6所示)[2-3] 。由于微分环节经双线性变换离散后,有一个z=-1的极点和一个z=1零点。z=-1的极点对应S平面上虚轴无穷远处,z=1的零点对应S平面上原点。z=-1的极点使系统的单位阶跃响应为等幅振荡曲线,同时z=1零点使系统的单位阶跃响应的超调量增大。所以,只采用微分环节,系统的单位阶跃响应在很长时间内输出量很小,但系统输出经一段时间后上下扰动加剧,并随着时间的延长,这种扰动的幅值不断扩大。
4 结论
因此,从上面仿真及原理性分析可知,采用双线性变换法离散设计的数字PID控制器中真正使系统不稳定的根源在于微分环节。所以,可以得出一般性的结论,即含微分环节的控制器不能采用双线性法离散。
【参考文献】
[1]高金源.计算机控制系统——原理、设计与实现[M].北京:北京航天航空大学出版社,2001.
[2]席爱民.计算机控制系统[M].北京:高等教育出版社,2004.
[3]洪乃刚.电力电子和电力拖动控制系统的MATLAB仿真[M].北京:机械工业出版社,2006.
[责任编辑:杨玉洁]
