基于线性移相误差的N步移相算法

张少丹,李　琳

(上海理工大学 光电信息与计算机工程学院,上海　200093)



基于线性移相误差的N步移相算法

张少丹,李琳

(上海理工大学 光电信息与计算机工程学院,上海200093)

摘要移相误差是影响移相干涉术测量精度的主要来源,针对移相器的线性移相误差,文中提出一种新型的移相干涉术算法-N步移相算法。该算法通过最小二乘法估计出移相器做等步移相时的实际移相相位,利用上述估计值代入相位计算公式获得被测物体的相位分布。同时对该算法进行仿真研究,其结果表明,算法能准确地估计移相相位,获得被测物体的精确相位分布,并可实现λ/100的高精度测量,且在测量精度上明显优于其他算法。

关键词线性移相误差;移相干涉术;移相器;相位分布

移相干涉术是一种被广泛应用于光学元件测试、全息干涉术和散斑计量等方面的测量方法[1-4],其具有测量精度高,重复性好等特点。但由于移相干涉术的测量结果是对各幅干涉图像和移相相位做运算所获得的,然而,在实际的引用中由于移相器本身的限制,移相误差无法避免,要实现精确的移相较为困难,因此,移相误差是影响测量精度的主要来源[5-9]。为减小或尽量消除移相误差对测量精度的影响,一般有两种方法:一是通过对移相器的标定尽量消除移相器的误差,如文献[10]通过3个压电陶瓷堆削弱移相器的误差、文献[11]由迭代最小二乘法削弱移相器的误差;二是如文献[12]的4步平均法,文献[13]的重叠4步平均法,以及文献[14]中Hariharan的5步算法,通过发展一种对移相误差不敏感的算法,来提高测量精度的。

本文是第二种,针对移相器的线性移相误差,提出的一种新型的移相干涉术算法—N步移相算法。该算法首先估计出移相器的实际相位位移,再运用相位计算公式获得被检测物体的相位。仿真结果表明,所提算法能准确地估计移相相位,获得峰谷值PV达到λ/100的相位分布(λ为光源的波长,常用的红光波长为770～622 nm),并且对比4步法、Hariharan的5步算法[14]、4步平均法[12]和5帧算法[6],具有更高的测量精度。

1移相干涉术算法

1.1传统算法

干涉条纹图像的光强分布可表示为

Ii(x,y)=A(x,y)+B(x,y)cos[φ(x,y)+φi],i=1,2,…,N

(1)

式中,A(x,y)代表背景光强,B(x,y)为干涉条纹的调制度,φ(x,y)为被检测相位,φi为参考相位位移。假设在一个周期内等间距采样N步,可得到N组光强值,参考相位位移可表示为φi=2π(i-1)/N,i=1,2,…,N。

应用最小二乘法对式(1)进行变换

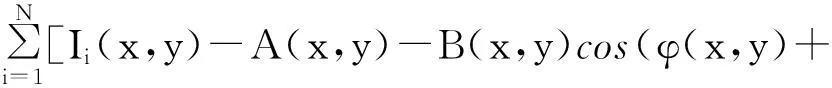
(2)

求得被测相位为

(3)

(4)

这种方法计算简单,因此得到了广泛应用。

(5)

这是对上述4步法运用平均技术进行改进的算法,能更好地减小移相误差对测量精度影响。

1.2步移相算法

本文算法是针对移相器的线性移相误差进行估计的N步移相算法。算法原理简述如下:

考虑移相器的线性移相误差,干涉条纹图的光强分布可表示为

Ii(x,y)=A(x,y)+B(x,y)cos[φ(x,y)+(i-1)[δ+α]],i=1,2,…,N

(6)

式中,δ表示移相器的步进相移量,α表示移相器移相δ时所对应的线性误差。

设α+δ=β,β为考虑线性移相误差时,移相器每一步的实际移相相位。针对干涉图像的一个像素点,对式(6)进行简单的分析变换可得到

2cosβ(x,y)Ii-1(x,y)-2cosβ(x,y)Ii-3(x,y)+Ii-4(x,y)=A(x,y)+B(x,y)cos[φ(x,y)+(i-1)β(x,y)]=Ii(x,y)

(7)

对式(7)用最小二乘法,即

(8)

由上面(8)式求得

(9)

考虑到采集到的图像存在光强误差,对整幅图像求取平均值,得到

(10)

式中,M和L分别是干涉条纹图中有效的行列像素点。

考虑到线性移相误差,对4步法进行改进,每4幅干涉图像为一组,求取平均值得到相位计算公式为

(11)

本算法的关键是对实际移相相位β的估计。若能精确地估计出β,再通过相位计算公式就能够精确地检测出被检测物体的相位。

2仿真结果与分析

Matlab仿真的目的是为了校验该算法能否准确估计实际移相相位,以及能得到被测物体的精确相位分布。

首先,校验该算法能否准确估计出实际相位位移。对移相器的线性误差用百分数来表示,即

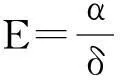
当E的取值范围为[-50%,50%]时,β的理论值β1和β的估计值β2如表1所示。理论值与实际值之间存在的误差平均值为0.000 004。

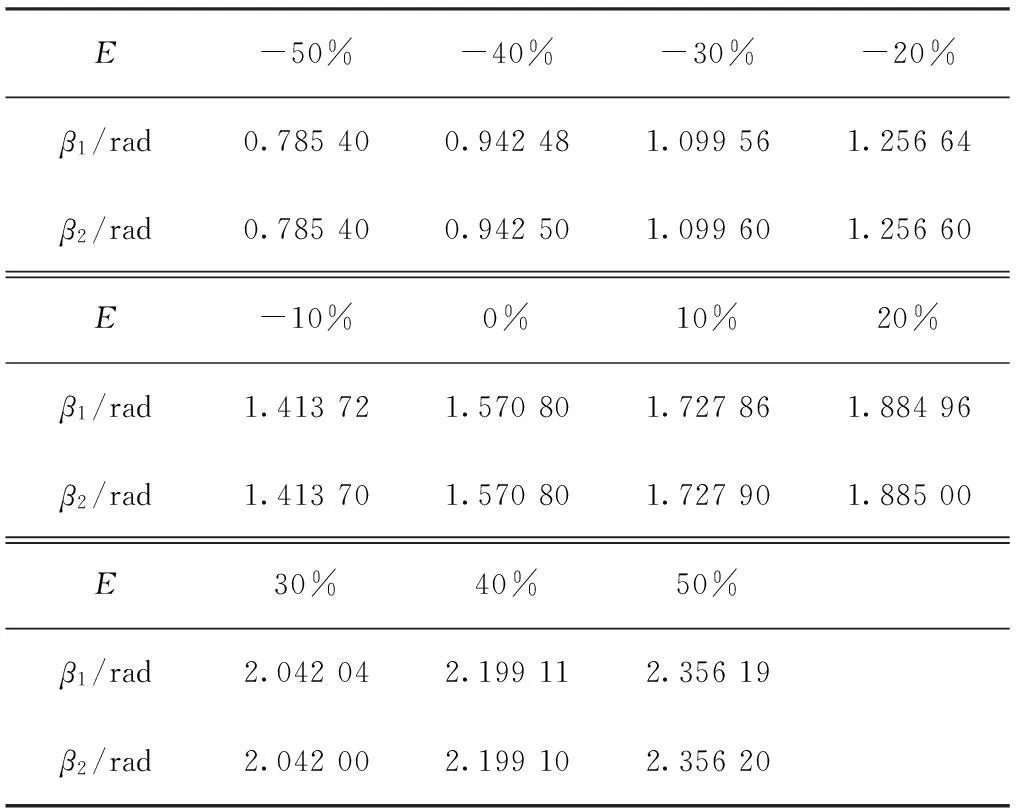
表1　β的理论值β1与估计值β2比较

其次,校验该算法能否准确的测量出被测物体的相位分布,图1为实际的相位分布。当E=-50%时,运用本文的算法得到的相位分布如图2所示。图3为实际相位与本算法得到的相位差值。由图可知,该算法能精确地复原被检测物体的相位。

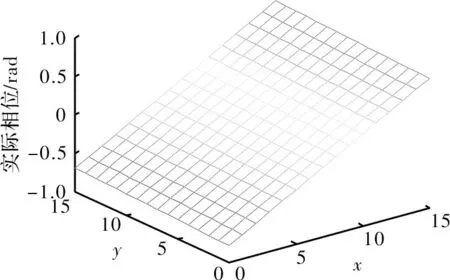
图1　实际的相位分布

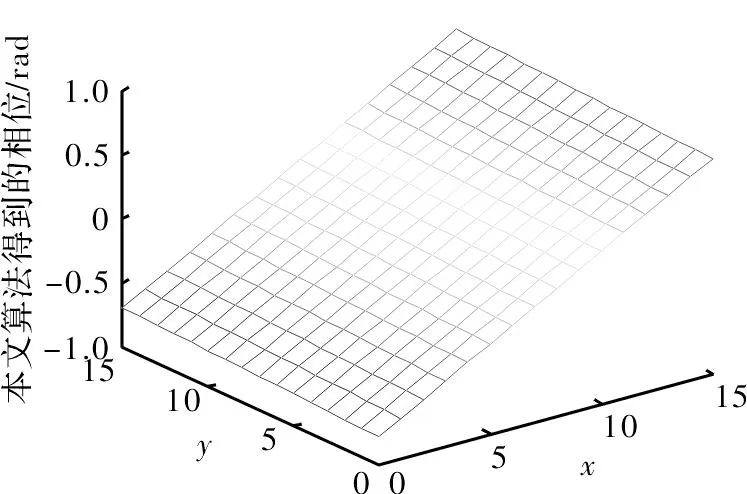
图2　本文的算法得到的相位分布

图3　实际相位与本算法得到的相位差值

最终,比较本文算法与4步法、Hariharan的5步算法[14]、4步平均法[12]和于飞的5帧算法[6]在不同的线性移相误差时所得到的峰谷值和均方根值RMS。图4和图6分别为本算法在不同线性误差是的PV值和RMS值,图5和图7分别为这5种算法各自在的取值范围为时,所对应PV值和RMS值。由图5和图7得出,对于PV值,4步平均法和5步法对线性移相误差有一定削弱作用,4步法和5帧算法对线性移相误差较为敏感。对于RMS值,当线性移相误差较小时,5帧算法对线性移相误差有一定的削弱作用,当误差较大时,5步法有一定的优势。而本文的算法在整个E=[-50%,50%]时,PV值和RMS值都明显优于其他4种算法,具有更高的测量精度。

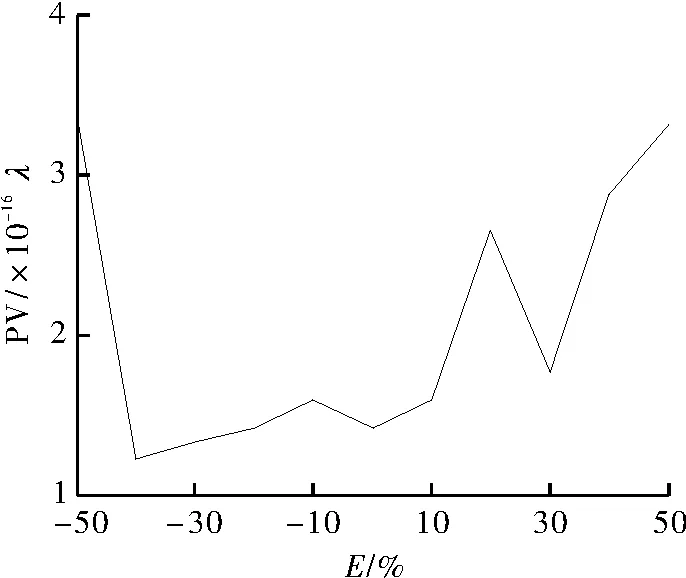
图4　本算法在不同线性误差时的PV值

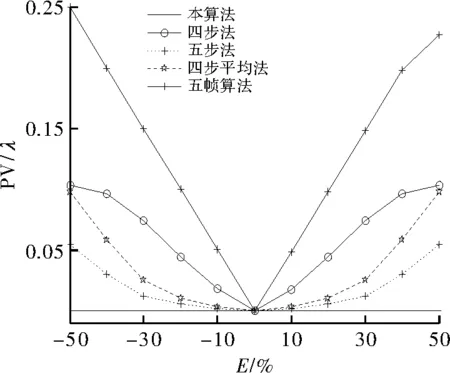
图5　5种算法在不同线性误差时的PV值

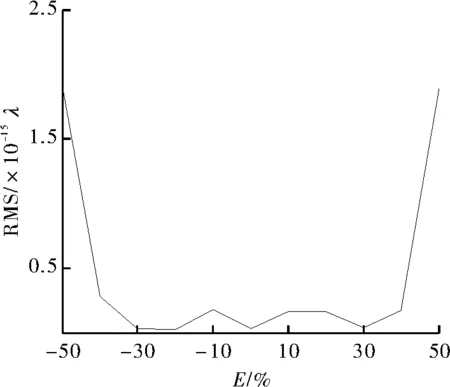
图6　本算法在不同线性误差时的RMS值

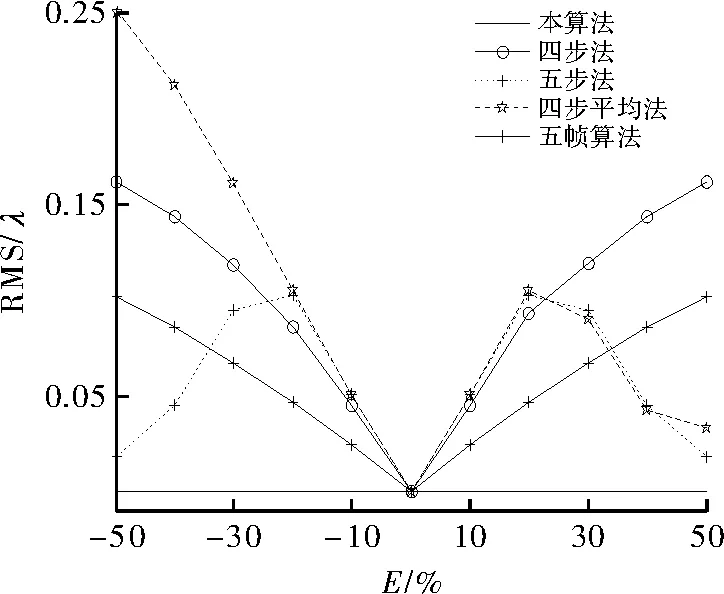
图7　5种算法在不同线性误差时的RMS值

从仿真结果可看到,本算法可准确地估计出考虑了线性移相误差时移相器的实际相位位移。同时,可看出该算法求解被测物体相位的峰谷值PV远小于0.01,达到λ/100的相位分布。

3结束语

本文的N步移相算法,首先运用最小二乘法估计实际的移相相位,再利用此移相相位计算被测物体的相位分布。由仿真结果可看出,本算法可有效地消除由于移相器的线性移相误差而引起的复原误差,提高相位检测时的精度,使检测精度的峰谷值PV达到λ/100。该算法简单,实用性较强,只要求移相器作等步移相,且不用受到移相步数N的限制,只需N>4即可。

参考文献

[1]Huang K T,Chen H C.Automatic measurement and stress analysis of ITO/PET flexible substrate by shadow moiré interferometer with phase-shifting interferometry[J].Journal of Display Technology,2014,10(7):609-614.

[2]朱越,刘文耀,刘方超,等.用数字全息术检测轮胎气泡缺陷[J].光学精密工程,2009,17(5):1099-1104.

[3]郭俊,王刚,孙杰,等.四步数字相移全息干涉术三维变形测量[J].仪器仪表学报,2011,32(12):2808-2813.

[4]Petzing J N,Heras-Palou C,King J,et al.The analysis of human femurs and prostheses electronic speckle pattern interferometry[J].Engineering Science and Education Journal,1998,7(1):35-40.

[5]Schwider J,Burow R,Elssner K E,et al.Digital wavefront measuring interferometry:some systematic error sources[J].Applied Optics,1983,22(21):3421-3432.

[6]于飞,惠梅,赵跃进,等.消除移相干涉测量中线性移相误差的五帧算法[J].光学技术,2008,34(3):398-400.

[7]黄文宇,龚建伟,陆际联.一种基于线性误差估计的5步移相算法[J].光学技术,2006,26(6):565-567.

[8]刘江,苗二龙,曲艺,等.基于光强自标定移相算法检测光学面形[J].光学精密工程,2014,22(8):2007-2013.

[9]郭仁慧,李建新,朱日宏.基于DCT算法的种子点相位解包算法[J].光学学报,2012,32(2):156-163.

[10]朱煜,陈进榜,朱日宏,等.由三个压电陶瓷堆组成的干涉仪移相器的校正与标定[J].光学学报,2001,21(4):468-471.

[11]苏志德,隋永新,杨怀江,等.迭代最小二乘法用于非线性移相器的标定[J].应用光学,2013,34(4):624-628.

[12]Ai C,Wuant J C.Effect on piezoelectric transducer nonlinearity on phase shift interferometry[J].Applied Optics,1987,26(6):1112-1116.

[13]朱日宏,陈进榜,王青,等.移相干涉术的一种新算法:重叠四步平均法[J].光学学报,1994,14(12):1288-1293.

[14]Hariharan P,Oreb B F,Eiju T.Digital phase-shifting interferometry:a simple error-compensating phase calculation algorithm[J].Applied Optics,1987,26(13):2504-2506.

N-Sample Phase-Shifting Algorithm Based on Linear Phase-Shift Error

ZHANG Shaodan,LI Lin

(School of Optical-Electrical and Computer Engineering,University of Shanghai for

Science and Technology,Shanghai 200093,China)

AbstractPhase-shift error is always the main source of the measurement precision in phase-shifting interferometry.In this paper,a new phase-shifting interferometry algorithm named N-sample phase-shifting algorithm is proposed,which can greatly reduce the phase reset error caused by linear phase shifting deviation.Firstly,step phase shifts of phase shifter are estimated.Secondly,the phase distribution of a fringe pattern is calculated by using the obtained phase shifts.Computer simulation shows the proposed algorithm accurately estimates the phase shift and obtains the phase distribution with an accuracy of λ/100,much better than those of existing algorithms.

Keywordslinear phase-shift error;phase-shifting interferometry;phase shifter;phase distribution

中图分类号TN247;O436

文献标识码A

文章编号1007-7820(2016)02-030-04

doi:10.16180/j.cnki.issn1007-7820.2016.02.008

作者简介:张少丹(1991—),女,硕士研究生。研究方向:图像处理。李琳(1983—),女,副教授,硕士生导师。研究方向:鲁棒控制等。

收稿日期:2015- 07- 06