自适应智能化谐波电流检测方法

马立新,周　磊,张海兵,栾　健

(上海理工大学 光电信息与计算机工程学院,上海　200093)



自适应智能化谐波电流检测方法

马立新,周磊,张海兵,栾健

(上海理工大学 光电信息与计算机工程学院,上海200093)

摘要有源电力滤波器检测谐波电流的实时性、精确性对电能质量的提高至关重要,文中提出了基于非线性最小二乘法与自适应人工神经网络结合的检测方法。非线性最小二乘法用于检测基波电压的频率,自适应人工神经网络用于检测基波电压的初始相位和基波电流的幅值,由基波电压的频率和初始相位获得单位幅值的基波电流。文中方法在0.02 s内可准确检测出基波和谐波电流,检测精度较传统方法有显著提高,通过仿真验证了该方法的有效性和优越性。

关键词自适应人工神经网络;非线性最小二乘法;谐波电流检测;有源电力滤波器

随着含有电力电子器件设备的广泛使用,电网中充斥着大量的非线性负载,由此产生了大量的谐波电流,谐波电流不仅干扰精密设备,还会导致电网电压发生畸变,严重影响电能质量[1-2]。智能电网的建设,分布式电源被允许并入电网,以及新能源汽车的推广,大量充电桩和充电站的建设,使电网中的谐波源增加,使得电网环境更加复杂[3]。

电力有源滤波器实时检测电网的谐波电流并进行补偿,可有效减少电网中的谐波电流[4]。谐波电流的准确、实时检测是电力有源滤波器,高效滤除谐波的关键,然而电网的随机性、复杂性干扰着谐波电流的准确、实时测量。国内外专家学者提出了不同的谐波电流检测方法,基于FFT的频域傅里叶分析方法[5],基于小波变换法[6],基于神经网络的检测方法[7],还有基于瞬时无功理论的检测方法[8]。FFT算法存在严重的频谱泄漏和栅栏现象,故谐波电流的检测精度达不到要求,且计算量较大;基于小波变换和神经网络检测算法,结构较为复杂;而基于瞬时无功功率理论的法中使用PLL获得基波电压的相位,并使用低通滤波器,这两个过程均会产生一定的延时。本文采用非线性最小二乘法和自适应神经网络的谐波电流检测方法,通过在Matlab下的仿真,验证该方法的时效性和准确性。

1非线性最小二乘法检测电压基波频率

在理想情况下,电网电压是频率不变的正弦波。但电压含有谐波,且基波频率在一定范围内存在波动。根据傅里叶级数理论,满足狄里赫利条件的周期信号均可分解为直流分量与幅值一定且频率为基波频率整数倍的正余弦之和[9]。

因电网中电压和电流是半波对称的,所以傅里叶级数中没有偶次谐波分量,且在平衡的三相三线制系统中,无3的整数倍谐波。由于,电网中电压的畸变率远小于电流的畸变率,所以采用电压频率f0作为电流基波频率的参考信号。若f0已知,第m点的电压值记为vm,将采集的N个点的电压值记为1×N的矩阵Y。

Y=[v1v2…vN]1×N

(1)

将电压分解后的傅里叶级数各谐波的系数记为X,包含的奇次谐波的个数为Nh。

X=[a1a5…ahb1b5…bh]1×2Nh

(2)

若记矩阵A为

(3)

则式(1)近似地表示为

Y≈XA

(4)

因矩阵A不是方阵,无法用逆矩阵解出式(4),可采用A的伪逆矩阵。AAT是非奇异矩阵,傅里叶级数各谐波的系数表示为

X≈YAT(AAT)-1

(5)

因f0是未知的,则A也未知,解线性最小二乘法的问题就变成解非线性最小二乘法(NLS),将式(5)代入式(4)

Y≈YAT(AAT)-1A

(6)

误差向量e表示为

e=Y[I-AT(AAT)-1A]

(7)

2自适应神经元电压相位检测

在传统的谐波电流检测算法中,大多采用PLL来获得基波电压的相位以此得到与电压同相位的参考信号。上文中非线性最小二乘法只获得了电压基波频率,要分离出基波有功和无功电流,还需要检测出基波电压的相位。因此,提出了使用自适应神经网络(Adaline)来检测电压相位。

在文中已检测出电网电压基波频率f0,将m点的电压vm近似地由WmXm表示,其中Ts为电压采用周期,Xm和Wm分别表示为

(8)

Wm=[a1…ahb1…bh]1×2Nh

(9)

傅里叶系数Wm,作为Adaline在线训练的权值,算法不断修正Wm使得检测的电压值与实际的平方差最小。目标函数表示为

(10)

Wm采用梯度下降法调整

Wm=Wm-1-η1E(Wm-1)

(11)

E(Wm-1)=-em-1·Xm-1

(12)

基波电压的相角θ1可表示为

(13)

3自适应神经元谐波电流检测

将第m采样点检测的电流im展开成傅里叶级数

(14)

式中Ip和Iq分别是基波有功电流和无功电流的幅值,Ts、fk分别为采样周期和k次谐波的频率。令

(15)

Zm=[IpIqa2b2…aNbN]1×2N

(16)

Zm作为自适应在线训练的权值,以误差的平方作为目标函数,即

E=(im-ZmHm)2=e2

(17)

Zm采用梯度下降法调整

Zm=Zm-1-η2E(Zm-1)

(18)

E(Zm-1)=-2e·Hm-1

(19)

基波有功电流ip可表示为

ip=Ip·sin(2πf0mTs+θ0)

(20)

基波无功电流iq可表示为

iq=Iq·cos(2πf0mTs+θ0)

(21)

k次谐波电流的相角φk可表示为

(22)

则k次谐波电流ik可表示为

(23)

4自适应智能化谐波电流检测方法

图1是自适应智能化谐波电流检测方法的实现框图。电网总电流i减去基波有功电流ip可得到基波无功电流和各次谐波电流的总和iq+ih;根据有源滤波器的补偿需要,如果不需要补偿无功或者某次谐波,可选择性的将其从iq+ih中减去,便可得到有源电力滤波器的补偿参考电流信号。

图1　自适应智能化谐波电流检测方法

5仿真验证

在Matlab下搭建三相全控整流电路,电源初始相位为50°,频率为50Hz,电压为220V,0.2s时电源电压相位发生突变,超前180°。三相全控整流电路的触发角为0°,直流侧负载为纯电阻,阻值R=50Ω。为验证本文提出方法的时效性和准确性,本文在上述电路环境下,分别使用本文提出的方法和传统的基于瞬时无功功率理论的ip-iq法获取有源电力滤波器的电流补偿参考信号。因为大多数情况下有源电力滤波器需要补偿无功和谐波电流,所以只需对比基波有功电流就能反映检测的精确性和实时性。

对比图2(a)和图2(b)两图可看出,PLL锁相环在电压初始相位为50°时,需>0.06s的时间才能完全跟踪电压信号,而使用NLS和ANN算法只需0.01s便可完全跟踪电压信号。由图2(c)和图2(d)两图可看出,在0.2s发生电压相位突变180°时,PLL锁相环需要约0.1s,才能跟踪信号,而非线性最小二乘法在0.02s之内已完全跟踪。

由图3所示,基于PLL锁相环的法在约0.1s才较为准确的检测出基波有功电流,而本文提出的方法在0.02s之内就能准确的检测出基波的有功电流。而当电压相位在0.2s发生180°突变时,基于PLL锁相环的ip-iq法在需要约0.15s才又较准确地输出基波有功电流,而本文所用方法只需0.02s。

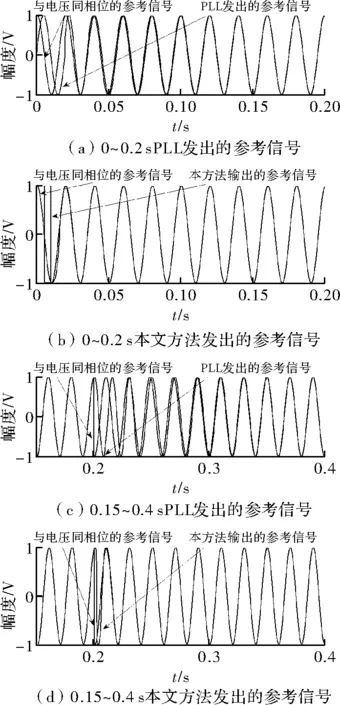
图2　本文方法和PLL输出的参考信号对比

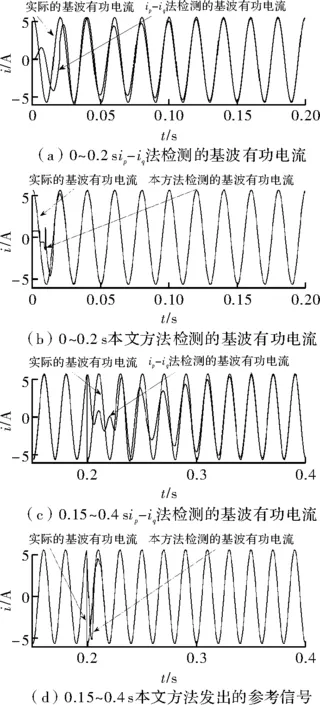
图3　本文方法和检测的基波有功电流对比

6结束语

本文提出的自适应智能谐波电流检测方法,与传统的基于瞬时无功理论的检测算法相比,算法中未使用PLL锁相环和低通滤波器,而是采用实时性更高的NLS和自适应神经网络。通过在Matlab中的仿真,对比这两种算法分别在电压初始相位不为0和电压相位发生突变的情况下的动态响应,可看出自适应智能谐波电流检测方法能显著提高检测无功电流的实时性和精确度。

参考文献

[1]朱宁辉,白晓民,董伟杰.基于EEMD的谐波检测方法[J].中国电机工程学报,2013,33(S1):184-189.

[2]雍静,娄方桥,王一平,等.低压配电系统单相非线性负荷的谐波衰减效应研究[J].中国电机工程学报,2011,31(13):55-61.

[3]髙赐威,张亮.电动汽车充电对电网影响的综述[J].电网技术,2011,35(2):127-131.

[4]邱银锋,梁志珊,魏学良.有源电力滤波器电源直流直接控制改进方法[J].电力系统及其自动化,2012,36(24):79-83.

[5]卿柏元,滕召胜,高云鹏,等.基于Nuttall窗双谱线插值FFT的电力谐波分析方法[J].中国电机工程学报,2008,28(25):152-158.

[6]黄文清,戴瑜兴,全慧敏.基于Daubechies小波的谐波分析算法[J].电工技术学报,2006,21(6):45-49.

[7]陈淑华,付青,马桂龙,等.基于神经网络自适应预测算法的谐波检测[J].电工技术学报,2011,26(S1):200-206.

[8]关彬,崔玉龙,王圆月.基于瞬时无功功率理论的谐波检测方法研究[J].电测与仪表,2007,44(10):1-4.

[9]杨林耀,张永瑞,王松林,等.信号与线性系统分析[M].北京:高等教育出版社,2010.

Adaptive Smart Harmonic Current Detection

MA Lixin,ZHOU Lei,ZHANG Haibing,LUAN Jian

(School of Optical-Electrical and Computer Engineering,University of Shanghai for

Science and Technology,Shanghai 200093,China)

AbstractThe accuracy and real-time performance of APF detecting the harmonic current is vital to improving the quality of electric energy.The method based on NLS (non-linear least squares) and ADALINE is proposed in this paper.NLS is used to estimate the frequency of the network voltage.ANN is used to estimate the initial phase of the network voltage and the amplitude of the network fundamental active current.Through the frequency and the initial phase of the network voltage,the sine signal whose frequency and initial phase is the same as the network voltage is generated.Compared with the traditional method,the time of detecting the phase,frequency,and amplitude of the network fundamental active current is apparently shortened and the accuracy is obviously improved.The method proposed precisely detects the fundamental current in 0.02 s.Simulation shows the effectiveness and superiority of this method.

KeywordsADALINE;non-linear least squares;harmonic current detection;APF

中图分类号TN713+.8;TP183

文献标识码A

文章编号1007-7820(2016)02-126-04

doi:10.16180/j.cnki.issn1007-7820.2016.02.034

作者简介:马立新(1960—),男,博士,教授。研究方向:电力系统分析与优化运行,智能电网与智能科学等。

基金项目:国家自然科学基金资助项目(61205076)

收稿日期:2015- 03- 19