用于求解旅行商问题的多策略离散型和声搜索算法*
2016-02-25王勇臻陈燕张金松
王勇臻 陈燕 张金松
(大连海事大学 交通运输管理学院, 辽宁 大连 116026)
用于求解旅行商问题的多策略离散型和声搜索算法*
王勇臻陈燕张金松
(大连海事大学 交通运输管理学院, 辽宁 大连 116026)
摘要:基于求解旅行商问题(TSP),提出了一种多策略离散型和声搜索算法.文中通过引入-opt算法设计了一种离散型即兴创作过程,并结合3种策略来提高全局寻优能力:采取教学优化策略给出了产生和声的新方式,以改善和声记忆库的质量;采用精英扰动策略探索最优和声的邻域进行精细搜索,以提高算法的收敛精度;通过排序选择更新策略保持和声记忆库的多样性,避免算法早熟收敛.实验结果分析表明,该算法能够有效求解TSP,具有可靠的全局收敛性和较快的收敛速度.
关键词:和声搜索算法;旅行商问题;-opt算法;离散型即兴创作;多策略
旅行商问题(TSP)是典型的NP难问题,在计算机科学、运筹学及工程优化等领域都有着广泛的应用.随着人工智能的发展,出现了许多求解TSP的群智能优化算法并不断改进.文献[1]采取连续优化子路径策略,提出了一种两阶段局部优化混合遗传算法(GA).文献[2]将粒子群优化(PSO)、蚁群优化(ACO)和3-opt算法融合应用于TSP的求解.文献[3]通过改进的空间扩散机制,设计了一种离散型杂草入侵算法用于求解TSP.文献[4]将蚁群系统中的蚂蚁分成两种角色,提出了一种用于求解TSP的扩展型ACO算法.目前,群智能优化算法已成为人们求解TSP的最有效方法.
和声搜索(HS)算法是由Geem等[5- 6]提出的一种群智能优化算法,已成功应用于许多实际优化问题.然而,HS算法通常用于解决连续优化问题,目前离散型HS的研究成果大多只针对解决二进制编码问题[7],较少用于排列编码问题.为改善和声记忆库的质量,提高算法的收敛精度,避免算法早熟收敛,文中基于求解TSP提出了一种多策略离散型和声搜索(MDHS)算法,并通过对TSPLIB中20个不同规模、不同类型的实例进行数值实验来分析MDHS算法的性能.
1基本和声搜索算法
基本HS算法的流程如下[5]:
(1)初始化和声记忆库大小SHM、和声记忆库考虑概率PHMCR、基音调整概率PAR、和声微调步长bw、最大迭代次数NI.
(1)
(3)基于PHMCR、PAR和bw进行即兴创作,依次执行式(2)、(3)产生新的和声,其中U(1,SHM)表示[1,SHM]上均匀分布的随机整数.
(2)
(3)
(4)更新和声记忆库.判断新和声xnew是否优于当前HM内最差和声xworst,若是则用xnew代替xworst.
(5)如果当前迭代次数n大于最大迭代次数NI,则终止运行HS算法,否则返回步骤(3).
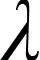
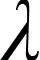

图1 2-opt和3-opt示意图Fig.1 Schematic diagram of 2-opt and 3-opt
3多策略离散型和声搜索算法
3.1 离散型即兴创作过程
针对TSP的求解,文中采用基于路径表示的编码.分析式(2)可知,新和声的产生过程实质上是记忆库中的所有和声与一个随机和声编码交叉的过程.由此可定义一种离散型记忆库考虑.
随机产生一个和声xinitial并随机选择一个城市c,计数器i=1.产生一个随机数ri,若ri

图2 t1的t3、t5邻域示意图Fig.2 Schematic diagram of the t3 and t5 neighborhood of t1

图3 离散型记忆库考虑示意图Fig.3 Schematic diagram of the discrete harmony memory consideration

3.2 教学优化策略TLO
基本HS算法仅通过即兴创作方式产生新和声,为了充分利用和声记忆库中的模式,文中提出了一种教学优化策略TLO.令xbest表示最优和声,xo1和xo2为生成的两个子代,随机产生起始出发城市为c.

图4 离散型基音调整流程图Fig.4 Flowchart of discrete pitch adjustment
首先按照正向添加规则[10]生成xo1,分别计算在xbest和xHM,i中c与下一邻近城市cnext1和cnext2的距离,选择最近的城市加入xo1中,并将其作为出发城市,继续寻找直至添加完毕.然后按照逆向规则生成xo2,计算c与上一近邻城市cprevious1和cprevious2的距离.最后计算并比较xHM,i与xo1和xo2的路径长度,选择路径长度最短的个体作为新的xHM,i.图5给出了教学优化的一个例子,假设6个城市的坐标分别为c1(10,75)、c2(36,9)、c3(91,78)、c4(54,53)、c5(8,51)、c6(78,51),xHM,3在经过一次教学后,路径长度由326.729减小到266.042,优于当前xbest的268.832.

图5 教学优化示意图Fig.5 Schematic diagram of teaching-learning-based optimization
3.3 排序选择更新策略SSU
基本HS算法采用最差和声更新策略,随着算法迭代种群的平均目标函数值逐渐减小,即兴创作产生的新和声很难有机会进入和声记忆库[11].为了保持算法的探索性,避免陷入局部最优,文中提出了一种排序选择更新策略SSU.首先,将和声记忆库中的和声从好到坏进行排序,然后计算顺序表中位置k被选中的概率Ps(k),其中
(4)
(5)
选中的和声将被新和声直接替换.容易看出,k越大对应的和声质量越差,被选中的概率越高.该策略保证了新和声能够进一步优化,同时k=1时概率Ps(1)=0,即最优和声永远不会被替换,保证了算法不会发生退化.
3.4 精英扰动策略EP
群智能优化算法后期,单纯通过增加新个体来提高多样性,对精英个体的进化不会产生影响,而提高算法性能的关键在于增加精英个体所在邻域的多样性[12].基于此想法,文中提出了一种精英扰动策略EP.
每迭代一次后,执行双桥算子对最优和声进行扰动,如图6所示,它可以帮助2-opt、3-opt发现新的邻域结构,然后再调用离散型基音调整进一步优化.若得到的新和声优于原和声则进行替换.该策略通过不断地探索最优和声的邻域来改善算法的收敛精度.

图6 双桥算子示意图Fig.6 Schematic diagram of double-bridge operation
3.5 时间复杂度分析
对于离散型即兴创作,生成随机和声的时间复杂度为O(N),执行一次编码倒位的时间复杂度为O(N),则记忆库考虑的时间复杂度为O(NSHM+N),对新和声执行基音调整的时间复杂度为O(CN+C2N),C为α-nearness候选集的势,总时间复杂度为O(N(SHM+C+C2+1)).
对于教学优化策略,选中最优和声的时间复杂度为O(SHM),按照正向/逆向添加规则生成子代的时间复杂度均为O(2N),择优选择新和声的时间复杂度为O(1),总时间复杂度为O(SHM+4N+1)≈
O(SHM+4N).
对于排序选择更新策略,采用快速排序对和声记忆库排序的时间复杂度为O(SHMlog2SHM),从和声记忆库中选中一个位置的时间复杂度为O(SHM),总时间复杂度为O(SHM(log2SHM+1)).
对于精英扰动策略,采用双桥算子生成邻域个体的时间复杂度为O(1),然后执行基音调整,总时间复杂度为O(N(C+C2)+1)≈O(N(C+C2)).
综上所述,MDHS迭代一次的时间复杂度为
O(N(SHM+C+C2+1)+SHM+4N+
SHM(log2SHM+1)+N(C+C2))=
O(N(SHM+2C+2C2+5)+SHM(log2SHM+2)).
3.6 算法描述
MDHS算法的求解步骤如下:
(1)初始化算法和问题参数;
(2)根据TSP编码方式初始化和声记忆库;
(3)基于离散型即兴创作过程产生新和声;
(4)使用排序选择更新策略;
(5)使用教学优化策略;
(6)使用精英扰动策略;
(7)如果当前迭代次数n大于最大迭代次数NI,则终止运行MDHS算法,否则返回步骤(2).
4实验结果与分析
文中使用Java语言编写程序实现MDHS算法,并在一台配置为Inter(R)Core(TM)i7-3770 CPU@3.40 GHz的PC上运行程序进行数值实验.MDHS参数设置如下:对于N<200的实例,SHM取N的1/5,对于N≥200的实例,SHM取40;PHMCR参考文献[13]进行取值,即
(6)
4.1 算法性能分析
为了验证所提出的3种策略的有效性和互助性,从TSPLIB中选取Eil101和Krob150实例采用5种算法(算法1:SDHS算法,不含3种策略;算法2:SDHS算法+TLO;算法3:SDHS算法+TLO+SSU;算法4:SDHS算法+TLO+EP;算法5:SDHS算法+TLO+EP+SSU,即MDHS)进行数值实验分析.
使用5种算法分别独立运行20次,α-nearness候选集的势取5,NI分别取2 000和3 000.表1给出了5种算法独立运行20次的计算结果统计,其中LB表示最短路径长度,LA表示平均路径长度.图7给出了5种算法求解Eil101和Krob150的收敛曲线.
表15种算法的计算结果统计
Table1Statisticsofcomputingresultsobtainedby5algorithms

算法LBLAEil101Krob150Eil101Krob150算法1903.5358268.81965.5963128.04算法2666.3026960.13684.7827656.26算法3644.9126302.53655.3526591.92算法4640.2126140.30644.2226289.29算法5640.2126140.30641.2426201.79
从图7可以看出:除算法1以外,其余4种算法在迭代100次后的路径长度收敛到了比较低的水平,后续迭代中算法2早熟收敛,算法5的开发能力最强并最终收敛到全局最优解附近;由算法2 和算法1的比较可知,教学优化策略不仅加快了算法的收敛速度,还大幅度提高了收敛精度;由算法2与 算法4、算法3与算法5的比较可知,精英扰动策略进一步地改善了算法的收敛精度;由算法2与算法3、 算法4与算法5的比较可知,排序选择更新策略能够让种群保持较高的多样性,避免早熟收敛.
综上所述,在相同计算条件下文中提出的3种策略对提升算法性能都能起到积极的作用,三者的融合能够更进一步地促进算法性能的提升.
4.2 与知名算法的对比实验与分析
为了更好地验证文中MDHS算法的性能,引进知名算法ASA-GA[14]和HGA[15]作为比较对象.MDHS独立运行20次,实验中α-nearness候选集的势取10,NI取5 000.表2是3种算法的最好结果对比,其中OPT为TSPLIB提供的最优解,O为LB与OPT之间的偏差,NP为20次独立运行中MDHS达到最优路径的次数.
从表2可知,MDHS算法在全部实例(20个)上均获得了3种算法中最好的结果,而ASA-GA和HGA都只获得11个最好的结果,并且MDHS算法的平均偏差仅为0.23%,优于ASA-GA和HGA的0.34%、0.98%.特别地,在实例Pr136和Krob150上MDHS算法得到的最短路径分别为96 770.91和26 127.36,比TSPLIB提供的最优路径长度分别小1.08和2.64.图8给出了MDHS算法在部分实例上得到的最优路径图.
为了检验3种算法计算结果的差异是否显著,文中进行了单因素方差分析.图9给出了3种算法的计算偏差分布图,检验的p值为0.027 5,小于0.05.

图7 5种算法求解Eil101和Krob150的收敛曲线Fig.7 Convergence curves obtained by five algorithms on Eil101 and Krob150
表23种算法的最好实验结果对比

Table 2 Comparison of the best experimental results obtained by three algorithms

图8 MDHS算法在部分实例上得到的最优路径图Fig.8 The optimal circuit graphs of partial instances via MDHS algorithm
从图9可知,3种算法的计算偏差有着非常显著的差异,直观上MDHS算法的计算偏差要小于ASA-GA与HGA算法.图10给出了3种算法的多重比较,由于MDHS与HGA算法的线段到横轴的投影互不重叠,可知MDHS与HGA算法计算偏差的差异是显著的.
为了考察α-nearness候选集的势取不同值对MDHS算法运行结果的影响,选取实例Pr124、Kroa200、Lin318和Pcb442进行数值实验.在实验中α-nearness候选集的势分别取5、10和15,NI取5 000,分别独立运行20次,实验结果如图11所示.

图9 3种算法的计算偏差分布图Fig.9 Distribution of computing deviations obtained by three algorithms

图10 3种算法的多重比较Fig.10 Multiple comparison of three algorithms

图11 势取不同值时的平均偏差对比Fig.11 Comparison of average deviations with different values of cardinality
由图11可以看出,α-nearness候选集的势从5增大到10时,平均偏差明显减小,但候选集的势从10增大到15时,平均偏差变化并不显著,反而增加了程序运行时间.因此,建议分析具体实例所属的候选集的势,或者是选择其他更优秀的候选集来进一步提高MDHS算法的性能.
5结论
参考文献:
[1]于宏涛,高立群,韩希昌.求解旅行商问题的离散人工萤火虫算法 [J].华南理工大学学报(自然科学版),2015,43(1):126-131.
YU Hong-tao,GAO Li-qun,HAN Xi-chang.Discrete artificial firefly algorithm for solving traveling salesman problems [J].Journal of South China University of Technology(Natural Science Edition),2015,43(1):126-131.
[2]MAHI M,BAYKAN O K,KODAZ H.A new method based on particle swarm optimization,ant colony optimization and 3-opt algorithms for traveling salesman problem [J].Applied Soft Computing,2015,30:484- 490.
[3]ZHOU Y Q,LUO Q F,CHEN H,et al.A discrete invasive weed optimization algorithm for solving traveling salesman problem [J].Neurocomputing,2015,151(11):1227-1236.
[4]ESCARIO J B,JIMENEZ J F,GIRON-SIERRA J M.Ant colony extended:experiments on the traveling salesman problem [J].Expert Systems with Applications,2015,42(1):390- 410.
[5]GEEM Z W,KIM J H,LOGANATHAN G V.A new heuristic optimization algorithm:harmony search [J].Simulation,2001,76(2):60- 68.
[6]MANJARRES D,LANDA-TORRES I,GIL-LOPEZ S,et al.A survey on applications of harmony search algorithm [J].Engineering Applications of Artificial Intelligence,2013,26(8):1818-1831.
[7]WANG L,YANG R,XU Y,et al.An improved adaptive binary harmony search algorithm [J].Information Sciences,2013,232:58-87.
[8]LIN S,KERNIGHAN B W.An effective heuristic algorithm for the traveling salesman problem [J].Operation Research,1973,21(2):498-516.
[9]VOLGENANT T,JONKER R.The symmetric traveling salesman problem and edge exchanges in minimal 1-trees [J].European Journal of Operational Research,1983,12(4):394- 403.
[10]于莹莹,陈燕,李桃迎.改进的遗传算法求解旅行商问题 [J].控制与决策,2014,29(8):1483-1488.
YU Ying-ying,CHEN Yan,LI Tao-ying.Improved gene-tic algorithm for solving TSP [J].Control and Decision,2014,29(8):1483-1488.
[11]黄鉴,彭其渊.多样性保持的和声搜索算法及其TSP求解 [J].计算机应用研究,2013,30(12):3583-3585.
HUANG Jian,PENG Qi-yuan.Diversity maintaining harmony search algorithm and its TSP solution [J].Application Research of Computers,2013,30(12):3583-3585.
[12]赵新超,刘国笠,刘虎球,等.基于非均匀变异和多阶段扰动的粒子群优化算法 [J].计算机学报,2014,37(9):2058-2070.
ZHAO Xin-chao,LIU Guo-li,LIU Hu-qiu,et al.Particle swarm optimization algorithm based on non-uniform mutation and multiple stages perturbation [J].Chinese Journal of Computers,2014,37(9):2058-2070.
[13]KONG X,GAO L,OUYANG H,et al.A simplified binary harmony search algorithm for large scale 0-1 knapsack problems [J].Expert Systems with Applications,2015,42(12):5337-5355.
[14]GENG X,CHEN Z,YANG W,et al.Solving the traveling salesman problem based on an adaptive simulated annealing algorithm with greedy search [J].Applied Soft Computing,2011,11(4):3680-3689.
[15]WANG Y.The hybrid genetic algorithm with two local optimization strategies for traveling salesman problem [J].Computer & Industrial Engineering,2014,70:124-133.
Multi-Strategy Discrete Harmony Search Algorithm for
Solving Traveling Salesman Problem
WANGYong-zhenCHENYanZHANGJin-song
(Transportation Management College, Dalian Maritime University, Dalian 116026, Liaoning, China)
Abstract:Proposed in this paper is a multi-strategy discrete harmony search (MDHS) algorithm for solving traveling salesman problem (TSP). In the algorithm, a discrete improvisation is designed by combining a -opt algorithm, and three strategies are employed together to improve its global optimization ability. The teaching-learning-based optimization strategy is adopted to provide a new way of producing new harmonies, so as to improve the quality of harmony memory (HM). The elite perturbation strategy is constructed to explore the neighborhoods of the best harmony constantly to perform a fine local search, so that the convergence precision of the proposed algorithm can be increased. The sort-selection-based update strategy is designed to preserve the diversity of HM for the sake of avoiding premature convergence. Experimental results show that MDHS can solve TSP effectively, and it holds an excellent search performance no matter in convergence speed or precision.
Key words:harmony search algorithm;traveling salesman problem;-opt algorithm;discrete improvisation;multi-strategy
doi:10.3969/j.issn.1000-565X.2016.01.019
中图分类号:TP18
作者简介:王勇臻(1990-),男,博士生,主要从事数据挖掘、智能计算研究.E-mail:KuaDMU@163.com
*基金项目:国家自然科学基金资助项目(71271034);辽宁省自然科学基金资助项目(2014025015)
收稿日期:2015-07-21
文章编号:1000-565X(2016)01- 0131- 08
Foundation items: Supported by the National Natural Science Foundation of China(71271034) and the Natural Science Foundation of Liaoning Province(2014025015)
