高速四点接触球轴承力学模型的数值求解算法*

路春雨　刘少军　戴瑜

(中南大学 机电工程学院∥高性能复杂制造国家重点实验室, 湖南 长沙 410083)



高速四点接触球轴承力学模型的数值求解算法*

路春雨刘少军戴瑜

(中南大学 机电工程学院∥高性能复杂制造国家重点实验室, 湖南 长沙 410083)

摘要：文中根据Hertz弹性接触理论分别建立了零转速和高速工况下四点接触球的力学模型;针对高速四点接触球轴承力学模型数值求解初值难以确定和不易收敛的问题,提出了一种基于Newton-Raphson理论的高速四点接触球轴承力学模型的数值求解算法,并给出了迭代变量取值范围及收敛因子的选取原则.为了降低求解难度,文中通过对高速四点接触球轴承力学模型进行数学变形,使得未知量的个数减少了一半.为了解决求解规模较大非线性方程组时经常出现卡死现象的问题,文中通过优化算法解决卡死现象,并提高了计算效率.文中算法计算结果与Jones程序结果的比较表明,调整收敛因子可控制文中算法的收敛性和收敛速度,从而验证了文中算法的正确性.

关键词：球轴承;载荷分布;拟静力学;数值求解

四点接触球轴承在航空航天领域占据着重要的地位,尤其是在喷气式发动机主轴和航空减速器中,在高速状态下承受联合载荷时,离心力、陀螺力矩、油膜润滑等因素的影响使得高速四点接触球轴承力学模型的求解变得非常困难和复杂[1-2].目前,虽然Newton-Raphson方法可以求解这类问题[3- 4],但这种方法对初值要求特别高,只有初值足够接近方程根的真值才收敛.然而,对于含有几十个未知量且初值难以确定的非线性方程组来说,求解过程很容易出现不收敛或收敛慢等问题.目前,仅有少数研究者提及加入松弛因子,但没有给出具体的方法[5].文献[5- 6]以球心坐标为未知量,在迭代过程中对未知量施加约束,并将不在钢球与内、外圈法向接触变形区域内的初值变换到这个区域,提出了相应的变换方法和约束方程,有效解决了迭代过程中法向接触变形可能小于0的情况,更加有利于力学模型的收敛,但约束方程的建立过程复杂,约束区域很难确保力学模型有效收敛,迭代初值的选择也具有极大的盲目性和随意性.Jones[7]的高速球轴承拟静力学分析程序的计算结果与真值接近,但Jones程序的收敛速度较慢且初值不易确定[8].对于高速四点接触球轴承的拟静力学模型,文中在Newton-Raphson方法的基础上,提出了一种初值易于得到且易于收敛的高速四点接触球轴承力学模型的数值求解算法,以解决高速四点球轴承力学模型难以求解的问题,并通过与Jones程序结果的比较来验证文中算法的正确性.

1静力学分析

1.1　四点接触球轴承力学模型的建立

四点接触球轴承是一种可承受双向轴向载荷的轴承,其内、外圈沟道均为“桃形”,理论上4个接触点在同一平面内,省略了保持架和内、外圈倒角的半个轴承的基本结构如图1所示.由于承受纯径向载荷Fr时为4点接触,如图1中的接触点1、2、3、4同时接触,故称为四点接触球轴承.在正常工作时,为了避免接触区发生大的滑动摩擦,要求其为两点接触,即对于图1中轴向力Fa1为点1和点3接触,对于轴向力Fa2为点2和点4接触.因此该类轴承主要用于承受以轴向力为主的载荷,不适用于承受以径向力为主的载荷.

图1　四点接触球轴承的基本结构Fig.1　Basic structure of four-point contact ball bearing

为了更加方便直观地分析四点接触球轴承在轴向力、径向力和力矩作用下的状态,现忽略滚动体和保持架,只保留内、外圈,如图2所示,在轴向力的作用下,内、外圈产生了δa的轴向相对位移量,在径向力作用下产生了δr的径向相对位移量,在力矩作用下内、外圈产生了相对转角θ,由图2可以清晰地看出内、外圈之间的相对位移[9].

图2　联合负荷作用下内、外圈的相对位移Fig.2　Relative displacement between inner ring and outer ring under combined loads

图3　受载前后沟道曲率中心轨迹的相对位置Fig.3　Relative position of curvature center track before and after loading

移动后在位置φ处的沟道曲率中心距为

(1)

式中:α0为初始接触角;A为内、外沟道的曲率半径中心距,A=(fi+fo)D, fi、 fo分别为轴承内、外圈沟道曲率半径系数,D为钢球直径.

(2)

由于受载后任意位置处钢球与内、外圈总的接触变形等于移位后沟道曲率中心距与原始中心距之差,故

δφ=Sφ-A

(3)

将Sφ代入式(3),得

(4)

由赫兹理论可知

(5)

式中,Kn为轴承的总刚度.

受载时四点接触球轴承的接触角会发生变化,由图2可知,任意位置的接触角αφ满足

(6)

(7)

以四点接触球轴承内圈为研究对象,内圈在力和力矩作用下的平衡方程可表示为

(8)

1.2　非线性方程的数值求法

Fa、Fr、M构成的非线性方程组(8)以δa、δr、θ为未知量,此方程组可以采用Newton-Raphson迭代法求解,其流程图如图4所示.

图4　静力学模型的迭代流程图Fig.4　Iteration flowchart of statics model

在求出δa、δr、θ之后,再求出每个钢球位置处的接触角.由于此非线性方程组未知量只有3个,比较容易求解,在此不再叙述.此静态计算的接触角和内、外圈的相对位移将作为高速四点球轴承迭代的参考初始值.

2拟静力学分析

静力学法对中低速轴承的载荷分布计算比较准确,而相对于高速轴承来说,由于其忽略了钢球的离心力、陀螺力矩等在高速状态下对轴承有重大影响的因素,因而其计算结果误差较大.拟静力学法是分析高速轴承的有效方法,因其考虑了钢球离心力、陀螺力矩等因素,故计算结果比较准确,能够反映高速四点接触球轴承的真实载荷分布状况.对于受轴向和径向载荷作用的高速四点接触球轴承,由于离心力和陀螺力矩的影响,各个钢球与滚道的接触角不相同,并且每个钢球与内、外圈的接触角、法向接触负荷均不相同,因此求解非常复杂[10-11].

为了方便叙述高速四点接触球轴承的载荷分布,建立图5所示的钢球方位角简图.

图5　钢球的角位置示意图Fig.5　Schematic diagram of angular position of ball

图6　受载前后内、外圈沟道曲率中心及钢球球心之间的相对位置关系Fig.6　Relative position relationship between centers of curvature in inner and outer raceway groove and center of ball before and after loading

在无载荷和高速状态下四点接触球轴承内、外沟道曲率半径中心及钢球中心之间的关系如图6所示.对于无载荷情况,内、外圈沟道曲率半径中心间距A=BD,其中B=fi+fo-1,Aaj和Arj分别为受载后第j个钢球的内、外沟道曲率半径中心之间在轴向和径向的距离,Xaj、Xrj分别为受载后第j个钢球的球心与外沟道曲率半径中心之间在轴向和径向的距离,αij、αoj分别表示第j个钢球与内、外圈之间的实际接触角.由图6可得

Aaj=BDsinα0+δa

(9)

Arj=BDcosα0+δrcosψj

(10)

从图6中还可以看出,在任意钢球位置内、外接触角满足

(11)

(12)

(13)

(14)

由勾股定理可以得到

(15)

(16)

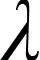
由于非共面的摩擦力很小,在此可以忽略不记[13],因而钢球的受载情况如图7所示.图中Fcj和Mgj分别为钢球的离心力和摩擦力矩,Qij和Qoj分别为钢球与内、外圈的法向接触载荷.

图7　在角ψj处钢球的受力分析Fig.7　Load analysis of ball at angle ψj

图7中钢球在水平和垂直方向上的平衡方程为

Qijsinαij-Qojsinαoj-

(17)

Qijcosαij-Qojcosαoj-

(18)

根据Hertz弹性接触理论,载荷与变形的关系为

(19)

(20)

为了获得δa、δr、θ的精确数值,建立了如下内圈受力平衡方程组:

(21)

(22)

cosψj=0

(23)

其中每个钢球有4个未知量(δij、δoj、Xaj、Xrj),如果轴承含有Z个钢球,则有4Z个未知量,再加上δa、δr、θ,则共有4Z+3个未知量.由于非线性方程组可以列出4Z+3个方程,故方程组有唯一解.通常采用Newton-Raphson迭代法求解此方程组[14],但这种方法对迭代初值的要求特别高,只有当初值足够接近真值时才收敛.然而,由于这里讨论的力学模型有几十个未知量且初值难以确定,故直接应用Newton-Raphson迭代法求解比较困难.为此,文中基于Newton-Raphson法提出了一种初值易于确定、易于编程的算法.

3算法介绍

3.1　未知量个数的消减

虽然δij、δoj、Xaj、Xrj、αij、αoj的关系非常复杂,但由接触角的三角函数关系式不难得到如下关系式[15]:

(24)

(25)

(26)

(27)

通过式(24)-(27)可以将关于δij、δoj、Xaj、Xrj的4Z个未知量表示为关于αij、αoj的2Z个未知量(j=1,2,…,Z),也就是将钢球与内、外圈的接触变形量及钢球中心相对于外沟道曲率中心的距离都表示为钢球的实际内、外接触角,从而将原来的4Z+3个未知量(δij、δoj、Xaj、Xrj、δa、δr、θ)变为2Z+3个未知量(αij、αoj、δa、δr、θ),未知量的个数减少了一半,降低了非线性方程组的求解难度和雅克比矩阵奇异的概率.另外,以钢球与内、外圈的接触角为未知量,更加直观,易于分析.

3.2　迭代约束

虽然经过力学模型变换后,非线性方程组的迭代变量大大减少,但方程组中各个变量之间相互耦合的复杂关系使迭代过程极其复杂,采用Newton-Raphson迭代法能否得到正确的求解结果,关键还要看迭代初值的选择.当初值选择不合适时,迭代收敛难以保证.为了减少误选初值的机会,保障迭代的收敛性,文中对初值及初始变量的约束进行分析.

图8　初始变量范围Fig.8　Range of initial variables

0<αoj<α0

(28)

(29)

3.3　算法优化

为了对算法进行优化,首先将钢球和内圈的所有非线性方程统一表示为fi(x)=a0+a1x+…+anxm= 0的形式(i=1,2,…,n;n为方程个数),x代表未知量αij、αoj、δa、δr、θ,然后计算fi(x)的雅克比矩阵J,即计算fi(x)对未知量αij、αoj、δa、δr、θ的一阶偏导数.

对于规模比较大的非线性方程组,雅克比矩阵及其逆矩阵数据量非常大,若直接采用Matlab雅克比函数,使用一般的计算机进行计算将会被卡死.为此,文中采用差商来代替求导,即

(30)

式中:i,j=1,2,…,n;x(k)为未知量x的第k次迭代值；微小量h=tx(i),t为控制收敛的因子,x(i)为未知量的第i个元素,t愈小,h就愈小,导数与差商的误差也愈小.从理论上看,在某工况下高速转动的轴承的实际载荷分布一定存在,这就意味着非线性方程组一定有解.无论h取多小,差商都存在且与导数比较接近;反之,t愈大,差商与导数的误差愈大,非线性方程组的收敛性愈差,收敛的可能性愈小.因此,收敛因子t的选择原则是:宜小不宜大.在本研究的工况下,经过试验证实:当t>0.005时,非线性方程组不收敛;当0.003≤t≤0.005时,迭代次数随着t的减小而增加;当t=0.003时,方程组的迭代次数最多,为14;当t=0.005时,方程组迭代次数最少,为2;当t<0.003时,迭代次数随着t的减小而减少且在减少到5之后保持不变.

为了避免求雅克比矩阵的逆矩阵,文中先求解一个线性方程组[15]:

J(x(k))Δx(k)=-f(x(k))

(31)

然后采用Newton-Raphson迭代法求解非线性方程组:

x(k+1)=x(k)+Δx(k)

(32)

式中,Δx为待求解的中间未知量.

3.4　算法实现

对于高速运转的四点接触球轴承,各个钢球与内、外圈的接触角不同,但从轴承结构及受联合载荷作用时静力学计算的接触角来看,由于钢球之间的距离非常小,相邻钢球之间的实际接触角相差不大,因此,从相邻钢球接触角变化不大的角度来获得比较靠近真值的迭代初值是可行的.即以上一个钢球的迭代接触角作为下一个钢球迭代接触角的初始值,从而确保算法收敛并最终获得非线性方程组的数值解.算法的具体步骤如下:

(1)以受载最大的钢球为研究对象,其与内、外圈的接触角分别设为αi、αo,设定δa、δr、θ的初始值为静力学的值.

图9　拟静力学模型的计算流程图Fig.9　Calculation flowchart of quasi-statics model

(3)以静力学求得的接触角为中间值向两边等度数变化(可以以1°为步长变化量,也可以取更小的值),把变化后的大值作为与内圈的接触角αi,小值作为与外圈的接触角αo,然后将αi、αo的值作为非线性方程组的迭代初值.

(4)如果步骤(3)的非线性方程组不收敛,则将αi、αo等度数变化,直到非线性方程组收敛为止.

(5)以步骤(4)求得的接触角作为下一个钢球迭代的初始值,然后再以前一次求得的接触角作为下一个钢球迭代的初始值,直到求解出所有钢球的接触角.

(6)以上述求得的接触角作为已知值,利用内圈平衡方程组迭代求解δa、δr、θ.

(7)将钢球和内圈构成的所有非线性方程联立,并以上述求得的接触角和内、外圈相对位移作为迭代初值迭代求解2Z+3个方程.

(8)编制并运行Matlab总体程序[16-17],输出αij、αoj、δa、δr、θ.

4算法验证

为了检验文中算法的正确性,以某型号四点接触球轴承为例进行实验,轴承节圆直径为165 mm,内沟道曲率半径系数为0.538,外沟道曲率半径系数为0.528,原始接触角为25°,钢球个数为17,轴向载荷为20 kN,径向载荷为4 kN,垫片角为12°,内圈转速为12 000 r/min.

首先进行静力学计算,各个钢球的接触角分布如图10所示,轴向和径向位移分别为0.053 810、0.005 936 mm.

图10　钢球与套圈接触角分布Fig.10　Distribution of contact angle between ball and ring

然后比较Jones拟静力学计算程序[7]与文中算法计算所得结果,如图11所示.从图中可以看出,文中算法的计算结果与Jones拟静力学程序计算结果一致,这是由于文中采用静力学的结果作为拟静力学迭代的初始值,并对算法进行了优化,因此对力学模型的收敛和结果产生了有利的影响,这也说明文中所构造的高速四点球轴承非线性方程组的计算方法是可靠的和有效的,结果正确.

为了比较文中算法与Jones拟静力学程序的计算效率[7- 8,18],文中在联想计算机(内存为2.85 GB,CPU为Inter(R)Core(TM)i5-2400,主频为3.10 GHz,Windows XP 32位操作系统)上进行运算,结果如表1所示.

从表中可以看出,在相同工况下,文中算法的计算时间和迭代次数都比Jones程序少,其原因在于,文中算法获得了比较接近真值的迭代初值,用差商代替求导,采用了先单球求解再总体求解的方法及通过力学模型变换减少未知量个数等优化措施.

图11　两种算法的计算结果比较Fig.11　Comparison of calculation results between two methods

表1不同轴向力下两种算法的迭代次数与计算时间

Table 1Iteration times and calculation time of two algorithms under different axial forces

轴向力/kN迭代次数时间/min文中算法Jones程序文中算法Jones程序18714354520511243422281825243102129

5结论

(1)文中通过“先局部后整体”的方法构造的高速四点球轴承非线性方程组计算方法简单,易于收敛,可通过调整收敛因子控制算法的收敛性和收敛速度.(2)通过对轴承高速转动钢球的实际运动并结合轴承结构特性的分析,获得了迭代初始变量的取值范围,为方程组初值的选取及迭代变量的约束提供了依据,极大地提高了方程组的迭代收敛性.

(3)联系实际情况讨论了大规模非线性方程组收敛因子的选择方法,并在本研究工况下给出了收敛因子的收敛范围及收敛因子的变化趋势与收敛速度的关系.

(4)文中根据“相邻钢球受载后的参数非常接近”的现象提出的高速四点接触球非线性方程组初值的选取方法解决了初值难以选取的问题,有效地避免了初值选择的盲目性,使初值的选择有所依据.

(5)文中关于高速四点接触球非线性方程组的求解方法可适用于三点接触球轴承和其他角接触球轴承.其他类型的高速轴承可作为参考.

(6)与Jones程序结果的对比验证了文中所提出的高速四点接触球轴承力学模型的数值求解算法的正确性和高效性,文中算法克服了Jones程序初值难以获得、不易收敛等问题.

参考文献:

[1]刘泽九,贺士荃,刘晖.滚动轴承应用 [M].北京:机械工业出版社,2007:12-13.

[2]崔立.航空发动机高速滚动轴承及转子系统的动态性能研究 [D].哈尔滨:哈尔滨工业大学,2008:2-3.

[3]苗学问.航空发动机主轴承使用寿命预测技术研究[D].北京:北京航空航天大学能源与动力工程学院,2008:24-25.

[4]LACROIX Samy,NELIAS Daniel.Four-point contact ball bearing model with deformable rings [J].Journal of Tribology,2013,135(3):031402-1/1- 8.

[5]彭波,王黎钦,崔立,等.角接触球轴承分析模型的数值求解 [J].南京航空航天大学学报,2009,41(3)：370-374.

PENG Bo,WANG Li-qin,CUI Li,et al.Numerical solution of analysis model for angular contact ball bearings [J].Journal of Nanjing University of Aeronautics and Astronautics,2009,41(3):370-374.

[6]朱益利,金超武,许磊,等.滚珠轴承力学模型的数值求解方法研究 [J].中国机械工程,2013,24(4):427- 431.

ZHU Yi-li,JIN Chao-wu,XU Lei,et al.Numerical solution methods of ball bearing mechanics model [J].China Mechanical Engineering,2013,24(4):427- 431.

[7]JONES A B.A general theory for elastically constrained ball and radial roller bearings under arbitrary load and speed condition [J].Journal of Basic Engineering,1960,82(2):309-320.

[8]HIROTOSHI Aramaki.Rolling bearing analysis program package “BRAIN” [J].Motion & Control,1997,24(2):15-24.

[9]邓四二,贾群义.滚动轴承设计原理 [M].北京:中国标准出版社,2008:87-89.

[10]HARRIS T A,KOTZALAS M N.Rolling bearing analysis:advanced concepts of bearing technology [M].5th ed.New York:Taylor and Francis Group,2007:28-55.

[11]JEDRZEJEWSKI J,KWASNY W.Modelling of angular contact ball bearings and axial displacements for high-speed spindles [J].CIRP Annals Manufacturing Technology,2010,59(1):377-382.

[12]TTAGIU G D,GAFITANU M D.Dynamic characteristics of high speed angular contact ball bearings [J].Wear,1997,211(1):22-29.

[13]张家库.高速角接触球轴承静动态参数性能分析 [D].合肥:合肥工业大学,2008:42-53.

[14]王开荣,杨大地.应用数值分析 [M].北京:高等教育出版社,2010:82-86.

[15]CHAPRA Steven C.Applied numerical methods with Matlab for engineers and scientists [M].2nd ed.New York:McGraw-Hill Companies,Inc,2008:284-292.

[16]张德丰.Matlab数值分析与仿真案例 [M].北京:清华大学出版社,2011:248-282.

[17]GUPTA P K.Transient ball motion and skid in ball bea-rings [J].Journal of Lubrication Technology,1975,97(2):261-269.

[18]JONES A B.Ball motion and sliding friction in ball bea-rings [J].Journal of Basic Engineering,1959,81(1):1-15.

A Numerical Solution Algorithm for Mechanical Models of

High-Speed Four-Point Contact Ball Bearings

LUChun-yuLIUShao-junDAIYu

(School of Mechanical and Electrical Engineering∥ State Key Laboratory for High Performance

Complex Manufacturing, Central South University, Changsha 410083, Hunan, China)

Abstract:On the basis of the Hertz contact theory, the mechanical models of high-speed four-point contact ball bearings in the cases of high speeds and zero-speed are constructed respectively. In order to solve the problems that the initial values of the constructed mechanical model at high speeds is undeterminable and their convergence is difficult, a numerical solution algorithm for the constructed mechanical model at high speeds is proposed on the basis of the Newton-Raphson theory, and the range of iteration variables and the selection principle of convergence factors are presented. For the purpose of reducing the solving difficulty, the number of unknown variables is reduced by a half through the mathematical transformation of the constructed mechanical model at high speeds. In order to tackle the stuck phenomenon of the program for larger-scale nonlinear equations, the proposed algorithm is optimized and the computational efficiency is improved. Finally, the results of the proposed algorithm are compared with those of Jones’ program. It is found that the convergence and convergence rate of the proposed algorithm can be controlled by adjusting the convergence factor. Thus, the proposed algorithm is proved to be correct.

Key words:ball bearings; load distribution; quasi-statics; numerical solution

doi：10.3969/j.issn.1000-565X.2016.01.018

中图分类号：TH133.33+4

作者简介：路春雨(1980-),男,博士生,主要从事滚动轴承设计与分析研究.E-mail:Lcy12132009@163.com

*基金项目：国防预研项目(81302XXX);湖南省研究生创新项目(CX2014B060)

收稿日期：2014-12-08

文章编号：1000-565X(2016)01- 0123- 08

Foundation items： Supported by the General Armament Pre-research Foundation(81302XXX)and the Project of Innovation for Postgraduate of Hunan Province(CX2014B060)