三维分形固定结合面法向接触刚度的研究*
2016-02-25李小彭王雪运海萌高建卓
李小彭 王雪 运海萌 高建卓
(东北大学 机械工程与自动化学院, 辽宁 沈阳 110819)
三维分形固定结合面法向接触刚度的研究*
李小彭王雪运海萌高建卓
(东北大学 机械工程与自动化学院, 辽宁 沈阳 110819)
摘要:基于传统的M-B模型,在考虑微凸体弹塑性变形的基础上,应用更能符合结合面实际表面形貌的修正的W-M函数,建立了三维分形结合面法向刚度模型.通过建立的刚度模型研究了分形尺度参数和分形维数对法向接触刚度的影响,并对出现的一些现象进行了分析.随着法向载荷与材料特性参数σspan/E的增加,结合面的法向刚度也增加;但随着分形尺度参数的增加,结合面的法向刚度却减小;随着分形维数的增加,当2.1≤D≤2.6时,结合面法向刚度增加,而当2.6≤D≤2.9时,结合面的法向刚度却减小;在考虑弹塑性变形的情况下,三维分形结合面的法向刚度要小于二维分形结合面的法向刚度.
关键词:三维分形;结合面;法向接触刚度;分形曲面;分形维数;弹塑性变形
结合面广泛存在于各种机器设备中,机器正常功能的实现很大程度上受结合面动静态特性的影响[1].如精密的手术机器人,其往往要对各种脏器、血管进行切割、缝合等非常精细的操作,要求具有很高的精确性[2].手术机器人机构各处的结合面动态特性综合起来对手术机器人的整体精确性就会有很大的影响.因此,在像手术机器人这样要求精确的仪器中,对结合面的研究就显得十分重要.
对结合面的法向刚度的研究是研究结合面动静特性的重要核心之一,很多学者进行了积极深入的探讨.张学良等[3]基于赫兹接触理论和接触分形理论,从理论上给出了机械结合面法向刚度分形预估模型;王书亭等[4]基于分形理论,提出两粗糙面配对的法向刚度力学计算模型;田红亮等[5]建立了固定结合部各向异性法向接触力学分形模型;温淑花等[6]基于接触分形理论和M-B模型[7],考虑弹塑性变形建立了结合面法向刚度分形模型.这些研究往往应用传统的W-M函数[8]描绘的分形曲线模拟结合面,得到二维结合面法向刚度分形模型,但实际工程中的结合面是三维立体的.
为了能更准确地描述结合面的法向刚度,文中考虑弹塑性变形,应用修正的W-M函数描绘的分形曲面模拟真实的结合面,基于Hertz接触理论和M-B分形接触模型,建立了结合面三维的法向刚度模型,研究了结合面相关参数对法向刚度的影响,并对三维法向刚度分形模型与二维模型进行了比较.
1结合面三维分形修正模型
在赫兹接触理论中,当作用有平面压力时,微凸体的弹性变形量可以表达为
(1)
式中:pm是微凸体受到的平均接触压力;等效弹性模量E=[(1-ν12)/E1+(1-ν22)/E2]-1,E1、E2分别为图1中两弹性体的弹性模量,ν1、ν2分别是相应的泊松比;R为等效单峰曲率半径,且R=[1/R1+1/R2]-1,R1、R2为两弹性体的曲率半径.
如图1所示,未变形的微接触体与刚性平面相交的截面面积为

(2)
而实际弹性接触面积为其一半:

(3)

图1 微凸体与刚性平面接触示意图Fig.1 Contact diagram of micro-bulge and rigid plane
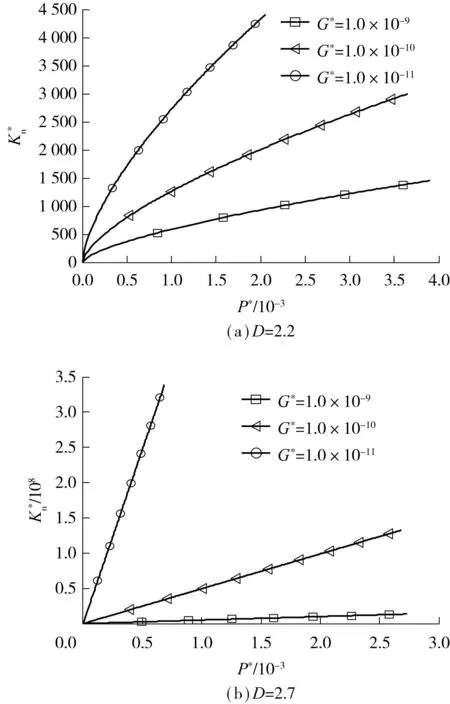
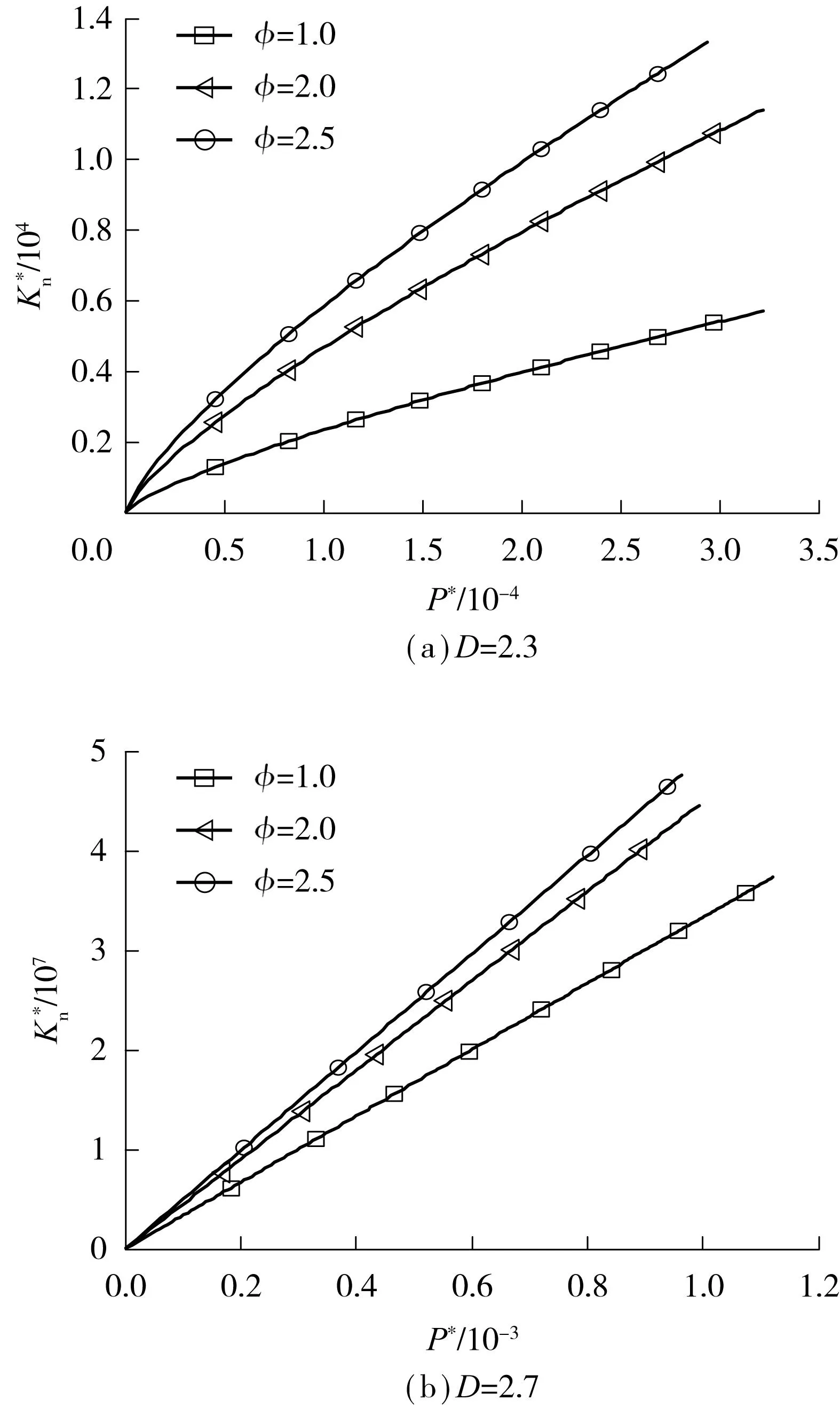
传统的W-M函数是用二维分形曲线去描述微凸体的表面形貌,即1 (4) 根据上述公式,可以得到三维的微凸体表面轮廓.微凸体的波峰与波谷的幅值差就是微凸体的变形量,即[9]: δ=2GD-2(lnγ)1/2(2r′)3-D (5) 根据式(2)与(3),式(5)可变为 (6) 同样,微凸体的曲率半径可表示为 (7) 2三维分形微凸体的接触状态 微凸体弹性临界变形量表达式为[10] (8) 式中:φ=σy/E,σy为屈服强度;kμ为摩擦力的修正因子,由文献[11]可知,当0≤μ≤0.3时,kμ=1-0.228μ;当0.3<μ≤0.9时,kμ=0.932e-1.58(μ-0.3). 由式(6)-(8)可得,微凸体弹性临界变形面积为 (9) Kogut等[12]研究发现,当微凸体处于弹塑性变形时,仍有两种不同的变形状态,并将弹塑性变形区域进行划分.当1<δ/δc<6时,为弹塑性一区;当6<δ/δc<110时,为弹塑性二区.弹塑性变形一区与二区的临界面积分别为[13] apt1=1101/(2-D)ac (10) apt2=61/(2-D)ac (11) 当微凸体处于塑性接触,受到的载荷为[10] (12) 依据Hertz理论,处于弹性变形的单个微凸体所受载荷与变形量的关系为[14] (13) 由式(6)、(7)与(13)可知,单个微凸体发生弹性变形时,载荷与接触面积的关系为 (14) 弹塑性接触一区与二区的接触载荷与微凸体变形量之间具有下列关系[12]. 当1≤δ/δc≤6时,上述关系表达式为 (15) 当6≤δ/δc≤100时,其表达式则为 (16) 式中,Pc为δ=δc时微凸体的接触载荷. 联合式(6)-(8)和式(13),可以得到弹塑性接触载荷与接触面积的关系. 当1≤δ/δc≤6时,得 (17) 当6≤δ/δc≤100时,得 (18) 处于弹性阶段的单个微凸体法向接触刚度为 (19) 同样,可以得到处于弹塑性阶段的单个微凸体法向接触刚度. 当1≤δ/δc≤6时, (20) 当6≤δ/δc≤110时, (21) 3三维分形结合面的接触状态 接触点的面积分布函数n(a)与最大接触面积al的关系为 (22) 结合面的实际接触面积Ar应包括塑性接触面积、弹塑性一区接触面积、弹塑性二区接触面积和弹性接触面积. (23) 1)当al>ac且D≠2.5时,结合面所受的总载荷为 (24) 对式(24)进行无量纲处理,为 (25) 2)当al>ac且D=2.5时,结合面所受的总载荷为 (26) 对式(26)进行无量纲处理,为 (27) 结合面的法向接触刚度应为 (28) 对式(28)进行无量纲处理,为 (29) 4结合面三维分形法向刚度仿真 从图2可以看出,随着无量纲法向载荷P*的增大,无量纲法向接触刚度Kn*也增大,与二维分形的法向载荷与法向刚度的影响规律基本一致,其主要是因为单个微凸体的法向接触刚度Kn=dp/dδ,当法向载荷P*增大时,单个微凸体的法向接触刚度就增大,从而导致整个结合面的法向刚度增大.由此可得,若要获得较大的结合面法向刚度,则可适当增大结合体的法向载荷.当2.1≤D≤2.4时,法向刚度与法向载荷呈非线性关系;当2.5≤D≤2.9时,法向刚度与法向载荷近似呈线性关系.随着D的增大,线性关系越来越明显. 图2 无量纲法向刚度Kn*与无量纲法向载荷P*的关系Fig.2 Relationship between dimensionless normal stiffness and dimensionless normal load P* 从图3中可得,当2.1≤D≤2.6时,随着分形维数D的增大,无量纲法向刚度Kn*也随之增大;当2.6≤D≤2.9时,随着分形维数D的增大,无量纲法向刚度Kn*却随之减小.初步分析是由于当D≥2.6时,单位面积下的微凸体数量超过一定的数值,单个微凸体的弹性变形能量下降,进而影响刚度,从而导致三维法向刚度逐渐减小.可见,分形维数对结合面法向刚度的影响很大,不同分形维数下的法向刚度值甚至出现数量级的差别. 观察图4可以发现,分形尺度参数G*增大,结合面无量纲法向刚度Kn*却随之减小.分形尺度参数越大,结合面的粗糙度就越大,微凸体的塑形变形比例增大,结合面的接触相应的刚度也就越小. 从图5可以看出,结合面无量纲法向刚度Kn* 图3 无量纲法向刚度Kn*与分形维数D的关系Fig.3 Relationship between dimensionless normal stiffness Kn* and fractal dimension D 从图6可以看出,二维分形模型下的法向刚度明显大于三维分形模型下的法向刚度,并且差值比较大.初步分析是三维分形中单位面积中微凸体的个数多,单个面积反而小,弹性变形能力减小,导致整体刚度比二维分形刚度小.所以,在二维分形模型下计算法向刚度和在三维分形模型下计算法向刚度是不同的. 图4 无量纲法向刚度Kn*与分形尺度参数G*的关系Fig.4 Relationship between dimensionless normal stiffness Kn* and fractal scale parameters G* 图5 无量纲法向刚度Kn*与材料特性参数φ的关系Fig.5 Relationship between dimensionless normal stiffness Kn* and material parameter φ 图6 二维分形法向刚度与三维分形法向刚度的对比Fig.6 Comparison of two dimensional and three-dimensional normal stiffness 5结论 经过上述研究,得到如下结论: (1)三维结合面法向刚度要小于二维结合面法向刚度. (2)随着法向载荷与材料特性参数φ的增加,结合面的法向刚度也增加;但随着分形尺度参数的增加,结合面的法向刚度却在减小.分形维数对结合面法向刚度的影响比较复杂,当2.1≤D≤2.6时,随着分形维数的增加,结合面法向刚度在增加;当2.6≤D≤2.9时,随着分形维数的增加,结合面的法向刚度却减小. 参考文献: [1]SVALINA Ilija,SABO Kristian,IMUNOVIGoran.Machined surface quality prediction models based on moving least squares and moving least absolute deviations me-thods [J].The International Journal of Advanced Manufacturing Technology,2011,57(9/10/11/12):1099-1106. [2]李欣悦.主从异构手术机器人的运动误差分析 [D]. 天津:天津大学,2007. [3]张学良,黄玉美,韩颖.基于接触分形理论的机械结合面法向接触刚度模型 [J].中国机械工程,2000,11(7):727-729. ZHANG Xue-liang,HUANG Yu-mei,HAN Ying. The normal contact stiffness model based on contact fractal theory [J].China Mechanical Engineering,2000,11(7):727-729. [4]王书亭,李杰,刘涛,等.机械固定结合面刚度特性建模 [J].华中科技大学学报,2011,39(8):1-5. WANG Shu-ting,LI Jie,LIU Tao,et al. Interfacial stiff-ness characteristic modeling of mechanical fixed joints [J].Journal of Huazhong University of Science and Technology,2011,39(8):1-5. [5]田红亮,钟先友,秦红玲.依据各向异性分形几何理论的固定结合部法向接触力学模型 [J].机械工程学报,2013,49(21):108-122. TIAN Hong-liang,ZHONG Xian-you,QIN Hong-ling. Normal contact mechanics model of fixed joint interface adopting anisotropic fractal geometrical theory [J].Journal of Mechanical Engineering,2013,49(21):108-122. [6]温淑花,张学良,陈永会,等.考虑弹塑性变形机制的结合面法向接触刚度建模 [J].振动工程学报,2015,28(1):91-99. WEN Shun-hua,ZHANG Xue-liang,CHEN Yong-hui,et al.The model of normal contact stiffness of joint interfaces incorporating elastoplastic deformation mechanism [J].Journal of Vibration Engineering,2015,28(1):91-99. [7]MAJUMDAR A,BHUSHAN B.Fractal model of elastic-plastic contact between rough surfaces [J].Journal of Tribology,1991,113(1):1-11. [8]MANDELBORT B B.The fractal geometry of nature [M].New York:W H Freeman,1982. [9]YAN W, KOMVOPOULOS K.Contact analysis of elastic-plastic fractal surfaces [J].Journal of Applied Physics,1998,84(7):3617-3624. [10]李小彭,赵光辉,梁亚敏.两圆柱体结合面法向刚度分形预估模型及其仿真分析 [J].农业机械学报,2013,44(10):277-281. LI Xiao-peng,ZHAO Guang-hui,LIANG Ya-min.Fractal model and simulation of normal contact stiffness between two cylinders’ joint surfaces [J].Transactions of the Chinese Society for Agricultural Machinery, 2013,44(10):277-281. [11]朱育权,马保吉,姜凌彦.粗糙表面接触的弹性、弹塑性、塑性分形模型 [J].西安工业学院学报,2001,21(2):150-157. ZHU Yu-quan,MA Bao-ji,JIANG Ling-yan.The elastic,elastic-plastic and plastic fractal model of rough surface [J].Journal of Xi’an Institute of Technology,2001,21(2):150-157. [12]KOGUT L,ETSION I.Elastic-plastic contact analysis of a sphere and a rigid flat [J].Journal of Applied Mecha-nics,2002,69(5):657-662. [13]LIOU Jeng Luen.The theoretical study for microcontact model with variable topography parameters [D].Taiwan:National Cheng Kung University,2006. [14]Johnson K L.Contact mechanics [M].Cambridge:Cambridge University Press,1985. [15]蒋书文,姜斌,李燕.磨损表面形貌的三维分形维数计算 [J].摩擦学学报,2003,23(6):533-536. JIANG Shu-wen,JIANG Bin,LI Yan.Calculation of fractal dimension of worn surface [J].Tribology,2003,23(6):533-536. 责任编辑:牛晓光 Investigation into Normal Contact Stiffness of Fixed Joint Surface with Three-Dimensional Fractal LIXiao-pengWANGXueYUNHai-mengGAOJian-zhuo (School of Mechanical Engineering and Automation, Northeastern University, Shenyang 110819, Liaoning, China) Abstract:On the basis of the traditional M-B model, a three-dimensional fractal model of normal contact stiffness of joint surface is constructed by taking into account the elastic-plastic deformation of micro-bulge and by using the modified W-M function which can better describe the actual surface topography of joint surface. Then, the influen-ces of the fractal scale parameters and the fractal dimension on the normal contact stiffness are investigated through the constructed model, and some phenomena are analyzed. The results show that (1) the normal stiffness of joint surface increases with the normal load and the material parameters σy/E, while it decreases with the increase of the fractal scale parameters; (2) with the increase of the fractal dimension, the normal stiffness of joint surface increases when 2.1≤D≤2.6 but it decreases when 2.6≤D≤2.9; and (3) the normal contact stiffness of the constructed three-dimensional fractal model is less than that of the two-dimensional fractal model with the elastic-plastic deformation. Key words:three dimensional fractal; joint surface; normal contact stiffness; fractal surface; fractal dimension; elastic-plastic deformation doi:10.3969/j.issn.1000-565X.2016.01.017 中图分类号:TH113 作者简介:李小彭(1976-),男, 教授,博士生导师,主要从事机械振动与动力学研究.E-mail:xpli@me.neu.edu.cn *基金项目:国家自然科学基金资助项目(51275079);辽宁省百千万人才工程培养经费资助项目(2014921018) 收稿日期:2015-06-17 Foundation items: Supported by the National Natural Science Foundation of China (51275079) and the Liaoning BaiQianWan Ta-lents Program(2014921018)



2.1 微凸体的临界接触面积
2.2 微凸体的法向接触载荷
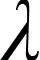


2.3 微凸体的法向接触刚度
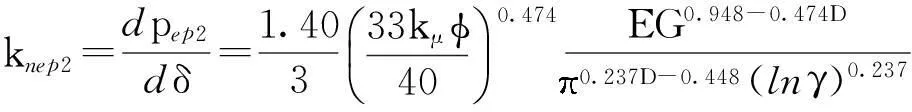
3.1 结合面的实际接触面积

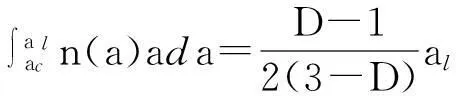
3.2 结合面的法向接触载荷
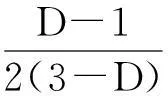
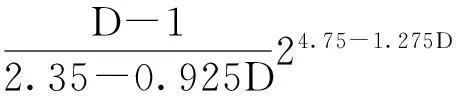

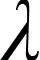

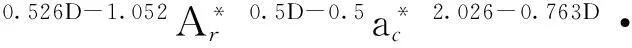

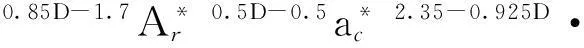

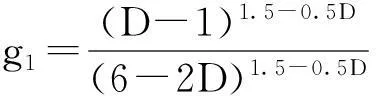
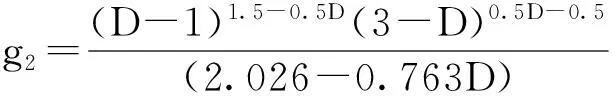


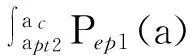
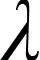


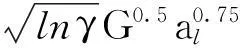
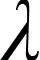

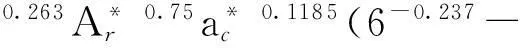

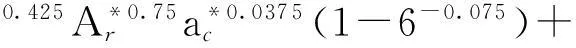
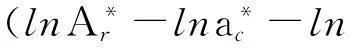
3.3 结合面的法向接触刚度
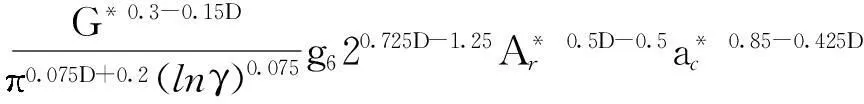
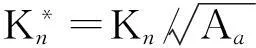
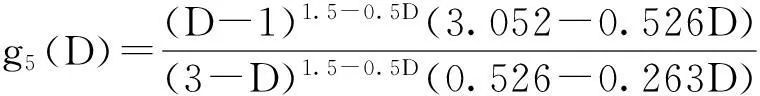

4.1 法向刚度与法向载荷的关系
4.2 法向刚度与分形维数的关系

4.3 法向刚度与分形尺度参数的关系
4.4 法向刚度与φ的关系

4.5 二维分形法向刚度与三维分形法向刚度的比较