非常规突发事件救援物资输送的路径优化研究

阎俊爱，郭艺源

(山西财经大学 管理科学与工程学院，山西太原 030006)



非常规突发事件救援物资输送的路径优化研究

阎俊爱，郭艺源

(山西财经大学 管理科学与工程学院，山西太原 030006)

摘要:鉴于非常规突发事件的突发性和不可预测性，为保证救援的有效性，需要及时确定应急救援路径，以最短的时间将足量的救援物资送到事故点。根据事故的严重程度不同，需要不同数量的救援物资。由于救援点的救援物资数量有限，当非常规突发事件灾害性强时，一个救援点无法满足事故点的物资需求，则要求多个临近救援点同时参与输送救援物资的任务。该文主要研究在实时/时变的复杂道路状况下，非常规突发事件发生后多救援点实施的应急救援物资输送的路径优化问题，通过改进遗传算法实现动态路径调整达到求解最短路的目的，实现了应急救援物资路径动态优化，为救援团队提供准确、及时、可视化的救援方案，提升救援效率。

关键词:应急救援；物资输送；实时；时变；路径优化；改进遗传算法；安全库存

非常规突发事件是指突发性的、不可预知的事件，往往造成严重的损失，不仅仅是财产损失，更有大量的人员伤亡。应对非常规突发事件是一项需要及时制定计划实施救援的复杂工程，由于时间的紧迫性，应急救援物资的输送成为关系到受灾人民群众生命安全最突出的问题。能否将救援物资第一时间送到事故点，通常直接决定受灾人群的伤残率和死亡率。仅以2008年的自然灾害为例，汶川8.0级特大地震、南方冰雪灾害(21个省遭受了这场意外的冰冻灾害)、华南地区突发的洪涝灾害、骇人的“黑格比”台风(严重危害广东、广西地区)、新疆的严重干旱(历史降水量第二少的一年)、长江及江南地区严重的秋涝、宁夏粮食受干旱影响严重减产、四川在一年内同时遭遇泥石流、地震及洪涝灾害，西藏遭受数日强降雪，这被称为十大“历史罕见”[1]。频繁发生的非常规突发事件造成严重的生命、财产损失的背后都反映出，在灾害发生后，事故点和外界信息不对称，导致在应急救援物资的输送环节出现问题，使得救援物资输送数量不够或者输送不够及时，导致应急救援物资输送环节出现混乱，这是造成不必要的受灾人员死亡和不必要的财产损失的关键。鉴于应急救援物资输送环节出现的问题，在事故发生后，对事故的应急响应，帮助决策者快速确定出应急救援路径，确保以最短时间将救援物资送达事故点的研究具有一定的理论和实践指导意义。

非常规突发事件一再发生，严重影响着我国社会的安全，如何应对非常规突发事件已经成为必须面对的挑战和亟待解决的难题。国内外学者在应急救援路径优化方面进行了深入的研究。王绍仁等[2]建立了多目标优化模型，适用于救援中心定位，并安排物资输送路线及多种运输方式相结合的方式来解决在短时间内完成救援物资输送的问题。王旭坪等[3]研究了在不确定的应急运输道路网建立情景分析树和救援理想路径，并建立了嵌入情景的应急路径选择模型。代颖等[4]在考虑震后救援物资配送问题上更进一步，更符合事故情景，同时考虑了救援物资需求的模糊性、不固定性和救援道路遭受破坏后的恢复状况，建立了在定位模糊情况下的路径优化模型以达到将救援物资输送到各需求点总时间最短的目的。

综上所述，目前国内外学者对非常规突发事件发生后的应急救援路径的选择已经进行了大量的研究，但由于事故发生后，道路的通行能力下降，学者对于实际道路交通信息的动态性研究仍旧无法满足非常规突发事件的需要[5]。因此，进入非常规突发事件的高发时期，对非常规突发事件发生后输送应急救援物资的路径优化问题的研究显得十分必要[6]。

1应急救援物资输送的路径优化模型构建

1.1　问题描述

非常规突发事件发生后，需要事故点附近的应急救援物资配送中心(救援点)在有限的时间、空间和资源约束条件下将救援物资运送到各个事故需求点。由于非常规突发事件的突发特点，事故点的应急物资需求量无法在第一时间准确计量，因此，对于事故点的救援物资需求量运用安全库存的算法定量化[7]。此外，对于救援点的选择也十分重要，直接影响到救援有效性[8-9]。受灾群众命悬一线，救援物资输送时间越短，他们的生命安全就多一份保障。因此，救援物资输送时间是该次救援首先要解决的问题，将救援物资运送的时间作为群众对于该次救援的满意程度[10-11]。即在事故点对应急救援物资的时间内完成输送任务，则此次救援任务成功，且时间越短，满意度越高。否则，该次任务失败。由于是多救援点的应急救援模式，应选择满足度最高的救援点完成任务[12]。

由于非常规突发事件发生后，救援路径会发生不可预测的变化，考虑到实际交通信息的动态性，需要实时动态调整救援行驶路径[13-14]。已经行驶过的路段不需要再次调整，只需在未行驶路段动态调整，满足到事故点路径最短的要求[15-18]。

综上所述，需要解决的问题是：①选择哪些救援点输送物资；②配送的救援物资数是多少；③被派遣的车辆应该行驶怎样的路径。本文用图1所示的技术路线来解决提出的问题。而对于应急救援物资配送的具体情况如图2所示(本文研究单事故点，多应急救援点来具体研究)。

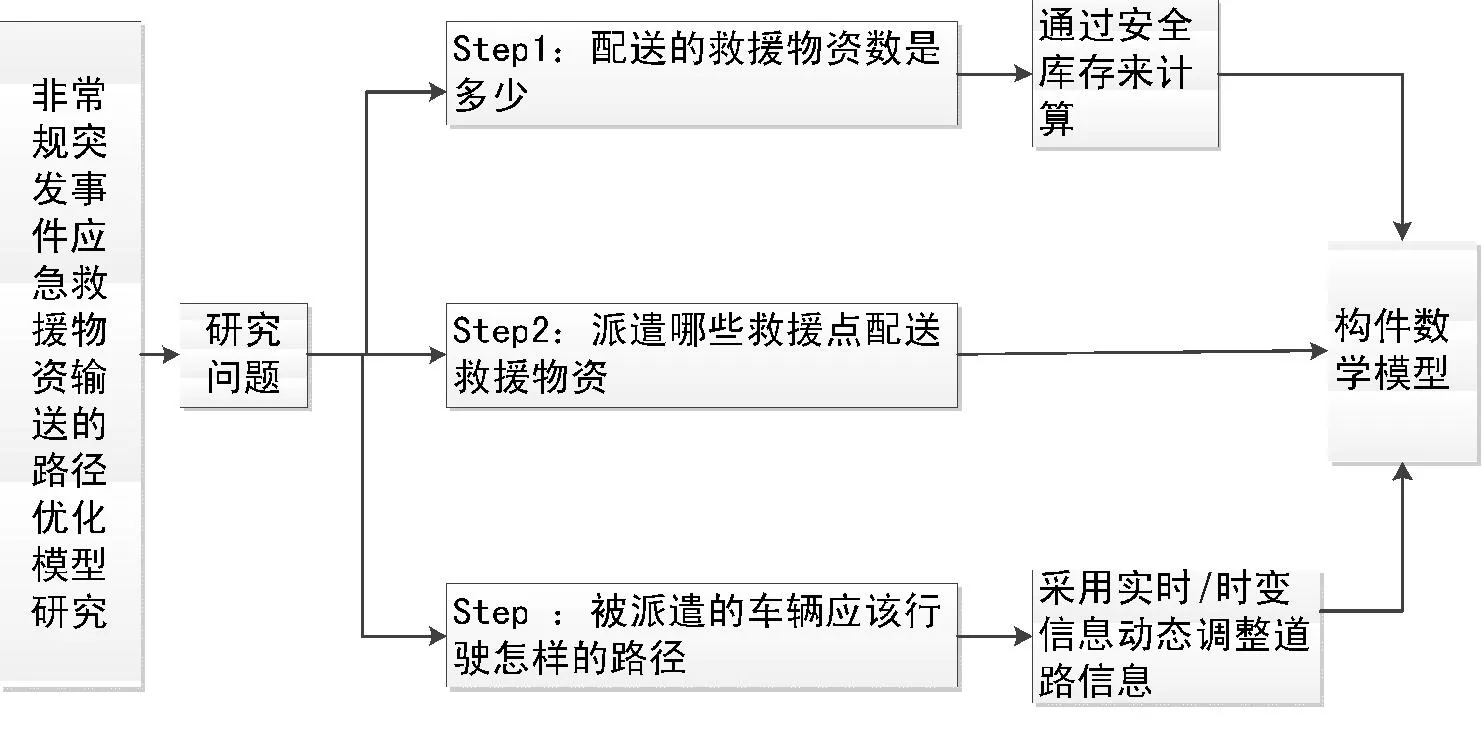
图1　所需解决问题的技术路线图

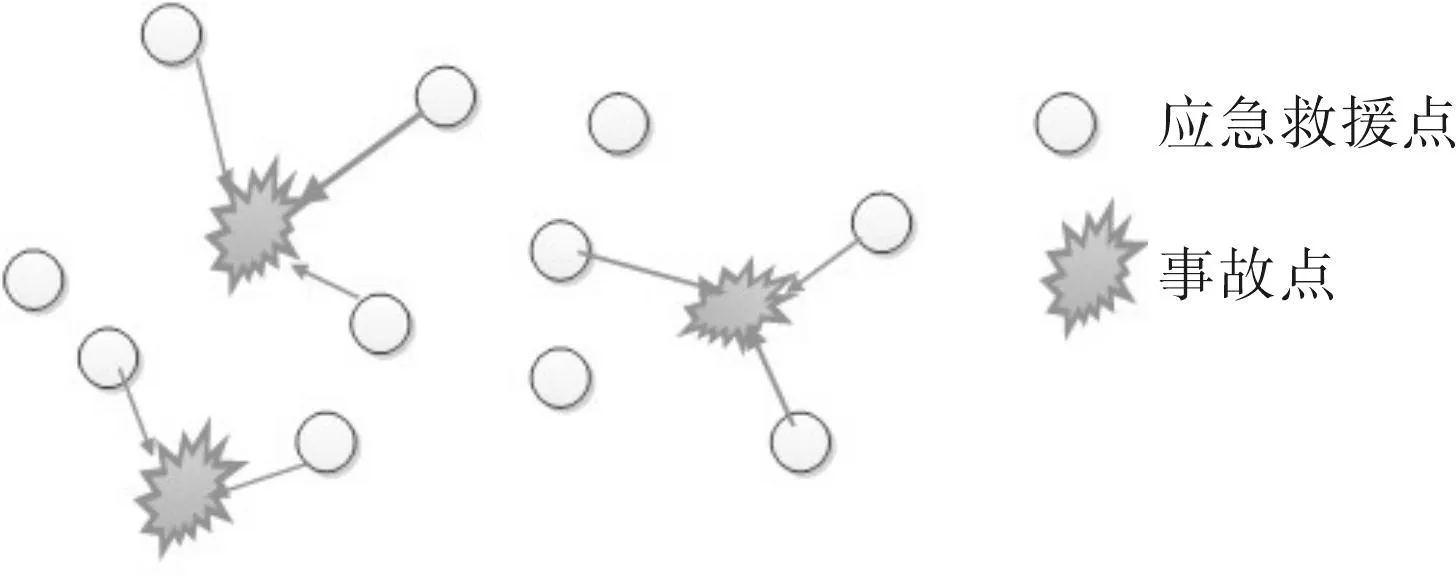
图2　多救援点应急救援图示

1.1.1分析并求解应急救援物资的需求数

(1)应急救援物资需求数的分析方法

由于事故点的救援物资数需求无法确定，很多时候救援点没有计算好救援物资的数量，时常造成救援物资分配不当的问题，比如在库存物资紧张的时候，有限的物资没有分配到最紧急的地区，送到的地区却出现物资冗余的问题。因此，计量事故发生地对救援物资的需求意义重大。目前主流对救援物资需求量估计的方法有两种。一种是通过以往的事故进行案例推理法，通过寻找类似案例，来推算本次事故救援物资需求量。这种方法不仅耗费大量时间，而且由于非常规突发事件本身的突发性和独特性，很有可能不存在类似案例。另一种主流方法是专家评估法，指权威专家运用专业知识及经验，通过对以往事故的研究发现规律，凭借自己的经验和主观判断进行预测。过度依赖专家经验，使得该方法主观性太强，缺乏客观性和准确性。本文根据事故点实时提供的受灾人数基于安全库存理论提出物资需求量预测方法。

救援物资数量的预测通常是通过分期计算时间段来衡量的，但这种方法只是考虑到每一个时间段受灾人员对于救援物资的需求，并没有考虑到潜在物资需求增长量。由于分期计算救援物资需求量后，并没有考虑输送物资途中时间的耗费，而大多数非常规突发事件发生后，交通道路受阻，严重延长了救援物资送到事故点的时间，因此，事故点救援物资的需求量还应该包括等待救援物资到达这段时间救援物资的潜在需求量。本文通过安全库存，通过缓冲库存量解决由不确定因素产生的潜在需求量的问题。

(2)应急救援物资需求数的求解方法

安全库存(Safe Stock)的计算问题。统计学中显著水平α对应物流中的缺失率，与顾客服务水平(订单满足率1-α)相互对应。即显著性水平=缺失率=1-顾客服务水平。

在非常规突发事件中，救援物资需求数的求解满足安全库存计算中需求发生的变化，提前期为固定常数的情况。满足两点：①假设需求变化满足正态分布的要求；②提前期长短变化(救援物资在路上的运输时间)。在已知提前期需求的均值和标准差的前提下，求解安全库存的公式为：

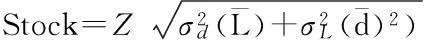
(1)

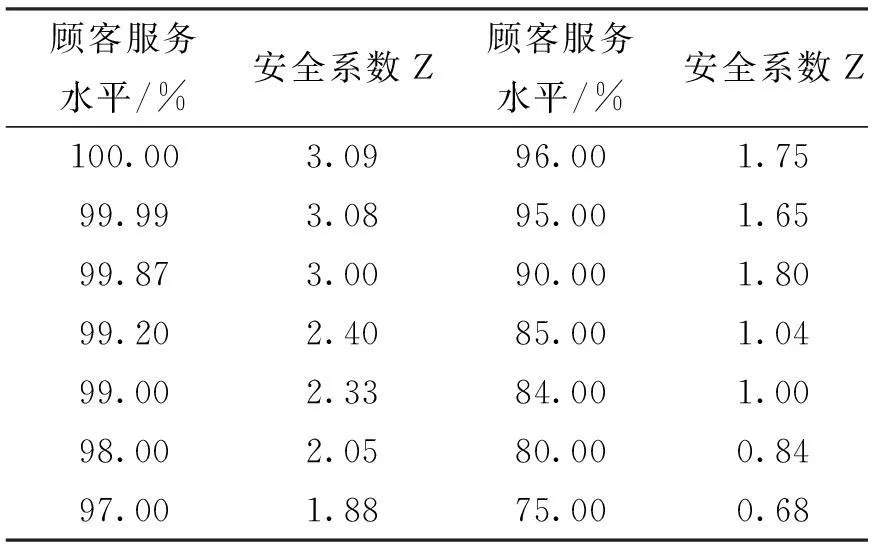
表1　顾客服务水平安全系数表

在提前期不变的情况下，将模型简化为：

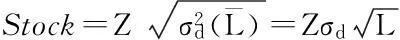
(2)

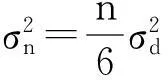
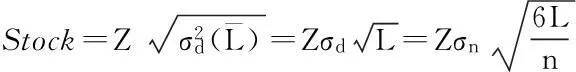
(3)

根据以上思路确定了预测事故发生地所需要的救援物资数量：

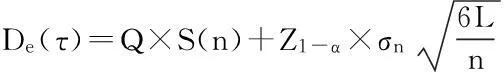
(4)

式中：De(τ)表示事故点需要救援物资数量；Q表示受灾地区每位存活人员每期对于该类物资的需求；S(n)表示第n期时事故发生地的受灾人数；Z1-α表示服务水平为1-α下的安全系数；σn表示该类物资第n期需求的标准差；L表示把物资输送到事故点需要的时间。

1.1.2输送应急救援物资的路径调整方法分析及计算流程

(1)输送救援物资的路径调整方法分析

以往研究最短路径问题的方法都是静态网络，将各个路段设定一个固定的权值，但非常规突发事件发生后会对道路发生阻碍，现实生活中道路也不是静态的，是随时间和事件而改变的，是一个动态网络。对于应急救援，多延误1min，就会对受灾人员造成多一分的危险，它增加了应急反应的时间，时间就是生命，减小应急救援车辆在路途中的时间事关重要，因此，本文采用实时信息/时变信息相结合的方法，动态调整救援车辆的路线。

道路网络的状态可以用行驶的时间来反映，道路的畅通与否直接影响行驶时间的长短。道路网络具有动态网络的一般特性，分为可预测的时变特性和不可预测的实时特性。道路网络具有时间依赖性，即每天的不同时刻行驶某一固定路段的时间不同，而不同时期同一时刻车辆的行驶时间相似。对于这种动态特性，求某一路段的最优化路径时，采用时变方法来计算。由于道路状态会受到天气情况、意外交通事故以及施工等一系列特殊情况影响，使得时变算法不再适用，对于此种动态特征需进行不断的优化，不断调整路段的最短路径，通过实时测量的方法，来适应不可预测的道路网络变化。ITS称作智能交通系统，通过它提供实时的道路信息。所以，实时信息针对一定时间范围内所提供信息的可靠性，而时变信息强调的是整体信息的可靠性。

选择将实时信息/时变信息相结合的方法动态调整输送应急救援物资的路径是基于以下两点原因。①实时信息可以准确提供当前时刻的道路信息，随时间推移不断改变，无法提前获得。而实时信息对于提供未通过的路段的道路信息会存在误差，因为当车辆真正通过那个路段时，当前的信息便会成为历史信息。②时变信息是根据大量历史数据得出不同时间段道路的平均行驶速度，相对准确地提供了未行驶路段的速度变化趋势。将实时信息/时变信息相结合，也就是车辆行驶路段使用实时信息，及时调整路面信息，在其余路段，采用统计的时变信息，这样可以准确地为车辆导航，保证输送救援物资车辆在根据道路的真实情况在最短时间到达事故点。

(2)采用实时信息/时变信息相结合方法动态调整路径的计算流程

将实时信息/时变信息相结合的方法求解车辆通过路段(i,j)的时间：

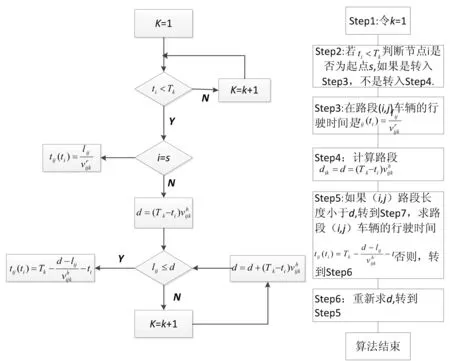
图3　车辆通过路段(i,j)的时间计算流程

1.1.3事故点受灾人员对于物资输送的时间满意度的分析及求解

(1)事故点受灾人员对救援物资输送时间的满意程度分析

对于非常规突发事件的受灾群众，应急救援物资输送的早晚直接决定受灾群众的生命安全，如果在一定时间段内没有及时送达，将造成更大的人身、财产安全。所以，受灾群众对于物资输送的时间有一定的要求，如果超出时间范围，即使送达物资，也无法满足受灾群众的需求，表明救援任务失败。而在有效的时间段内，救援物资越早送达受灾群众手里，受灾群众及早得到治疗，时间满意度会越高。

(2)时间满意度的求解方法

由于非常规突发事件的特点，事故点的受伤人员的病情不确定，无法精确确定他们要求物资到达的时间，只能依赖专家通过经验和专业知识确定事故点对救援物资需求的时间上限和下限。若救援物资能在有效时间段内及时送达，则满意度在[0,1]区间内，救援物资越早送达，受灾群众的满意度越高。如果救援物资在受灾群众的忍受区间外送达，则救援任务失败，假定为一个很大的负数N。假设U(te)表示事故发生地e的顾客对救援点输送救援物资时间的满意程度；fe为e处受伤人员对救援点输送物资可以等待的最短时间；MLe为e处受伤人员对救援物资输送到达感到很满意所能接受的等待上限；BSe为e处受伤人员对救援物资输送到达感到很不满意的等待时间下限。则受灾地区受灾群众对于救灾物资送达所需时间的要求范围为，用如下函数U(te)表示事故点e的受灾群众的时间满意度：

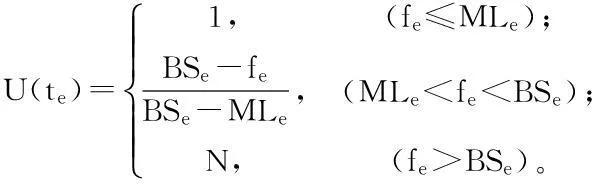
(5)

由于受灾群众希望救援物资第一时间送达，则救援物资送达时间越短越好，最好是事故点就是救援点，使得救援物资0时间到达，则以上公式可以进一步简化为：

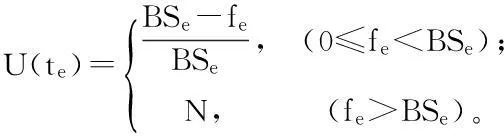
(6)

1.2　模型假设

(1)在每一辆救援车辆救援次数至多为一次的情况下，事故点的物资总需求可以得到满足，且用车辆需求数表示救援物资需求数。假设所有救援车辆型号相同，可容纳同样数量的救援物资。

(2)同时、同地派出的救援车辆的道路状况相同，行驶路线一致。

(3)救援路径不含有回路。

(4)各个救援点派出车辆的准备时间忽略不计。

1.3　符号定义

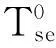
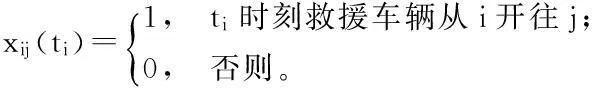
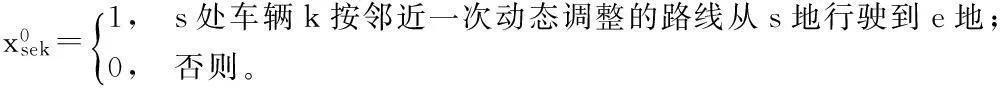
1.4　模型构建

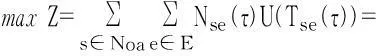
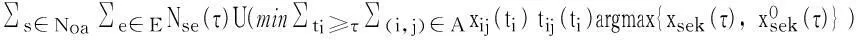
(7)

目标函数(7)输送救援物资时，在满足事故发生地受灾群众对救援物资所需时间要求的情况下，要求最大限度完成救援任务，换言之，目标函数要求总行驶时间最小。

(8)保证救援车辆行驶的路径满足连续性。

(9)保证救援车辆行驶的救援路线不包含回路。

(10)表明没有被选中的救援点不可以派遣救援车辆。

(11)表明被选中的救援点必须派出车辆救援。

(12)表明参与救援的所有救援点拥有的救援物资总数满足事故需求。

(13)约束每个选中的救援点派遣的车辆小于等于该救援点闲置的车辆数。

(14)为事故发生地受伤人员对救援的时间满意度。

(15)为派出救援车辆到事故点的救援点为被选中的为此次事故实施救援的救援点，否则，该救援点没有被选中。

(16)约束每个救援点可派出的车辆数要满足非负的条件。

(17)表明是否行驶新的规划路线，只有新调整后的救援路径输送物资时间小于临近一次调整的时间，此时需要按新的路线行驶，否则，不需要。

1.5　模型求解

基于实时信息/时变信息相结合求解最短路的研究，在动态调整行驶路线时选用改进遗传算法求解。

与传统的遗传算法不同，改进遗传算法在编码长度、初始种群的选择和交叉变异环节进行了改进。

对比两种遗传算法的区别如表2所示，而图4是改进遗传算法求解最短路的流程图。

2输送应急救援物资输的路径优化算法流程

为完成应急救援物资的输送，根据第1节构建的路径优化模型，需要通过如下的计算步骤确定具体的救援方案。①根据安全库存的求解方法计算事故发生地对救援物资的需求数。②基于实时信息/时变信息相结合求解最短路，再选用改进遗传算法调整被选中的救援点到事故发生地的最优路径。③根据救援点完成任务的时间求解救援点到事故发生地的时间满意度。④通过与邻近一次求出的救援车辆行驶时间进行对比，判断是否需要更新车辆的行驶路径。输送应急救援物资的路径优化算法流程如图5所示。

表2　两种算法的区别

图4　改进遗传算法求解最短路的流程图

3算例分析

以山西省太原市某一路段(图6)发生地震灾害事件为例，此刻该路段总共有6 000人，造成1 011人死亡，531人受伤如表3所示，假设有7个应急救援点，09:15救援中心接到电话，称地图中Z地(图6中编号33)发生地震。此时事故发生地邻近的7个救援点(图中A-G点)的救援能力图表4所示。太原市此路段的道路网时变信息和车辆的实时行驶速度由相应时刻地理信息平台提供(假定5min为一个时段)。由于灾情紧急，设定每4min更新一次道路的实时信息，故令ΔT=4min，并根据信息重新计算判断是否改变行驶路径。改进遗传算法的参数设置如下：Num=50；Maxgen=50；Pc=0.8；I=0.1。

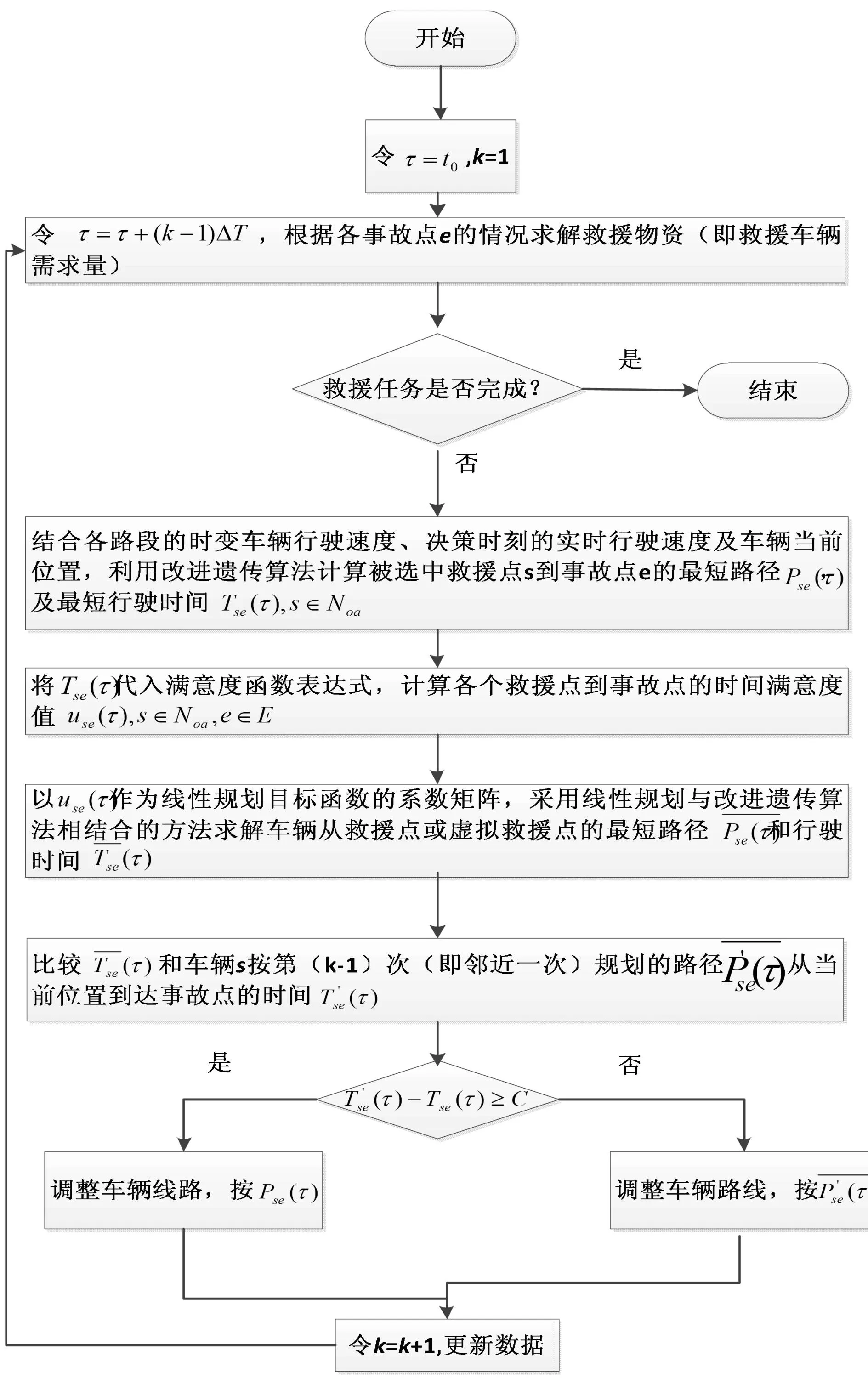
图5　应急救援物资配送优化算法流程图

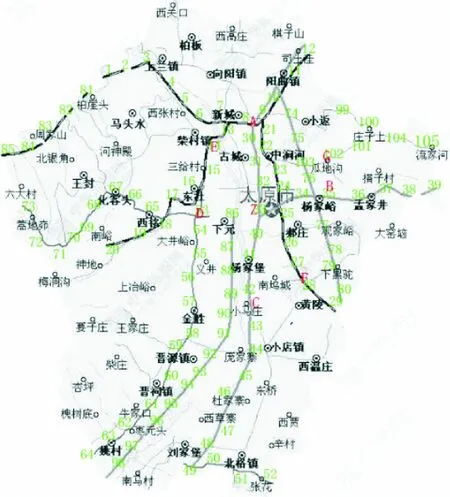
图6　山西省太原市某一路段图标示

事故点人员伤亡数死亡人数受伤人数某路段(33)1011531

表4　救援点的救援能力

首先计算救援物资需求量。

通过实验及调查数据表明，每个人需要纯净水4L/d，面包3个/d，根据1-1中的库存理论，则纯净水每人需要1/3(L/期)，面包每人需要1/1(个/期)。由于药品种类繁多，根据灾害情况不同，需求量不同，在此假定为药品M，每人每小时的需求量为80mg，每期则为310mg。设定缺货率α=0.05，即顾客服务水平为95%，救援物资到达前受灾人员可等待的时间L=3h。则存活人数S(0)=6 000-1 011=4 988(人)。

R1(0)=3 316(L)；R2(0)=1 498(个)；

R3(0)= 1 596 160(mg)。

然后确定救援路径。

第一次作出决策时为接到信息时刻为09:15救援中心接到救援电话的时间，假定每辆车可运输水831L，313个面包，199 510mg药品，则一共需要救援中心派遣8辆车，被选中进行救援的邻近救援点实施救援的路径如表5所示，计算时间为74.383 4s。

表5　被选中的救援点的行驶路径

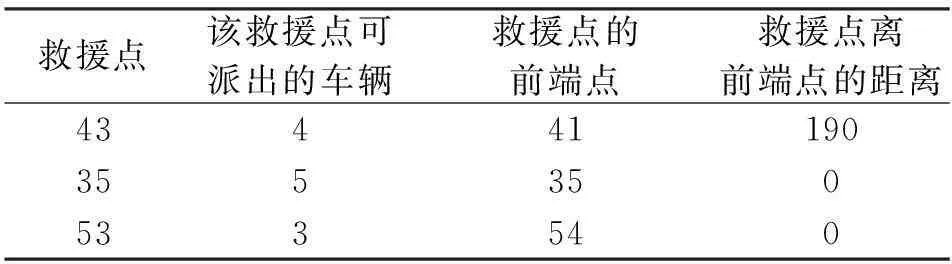
表6　各救援点的车辆信息

表7　选中的救援点的行驶路径

第二次作出决策的时刻为09:19，各救援点的车辆信息见表6，同样算法，求出此时共需4辆车，被选中的救援点及派遣车辆的数量及救援路径如表7。计算时间为56.594 1 s。

第三次作出决策的时刻为09:23，事故点需求全部满足。

以上路径优化的决策过程通过MATLAB软件显示如图7所示。

图7　应急救援物资输送的路径优化决策过程

4总结

鉴于近年来非常规突发事件的频发性，而应急救援物资输送环节往往是造成能否使得事故点受灾人员得到及时救治、减少人员财产损失的关键问题。为了保证足量的应急救援物资及时输送到事故发生地，就满足受灾人群的需求，减少由于物资输送不及时导致事故不必要的灾后损失，本文是在非常规突发事件发生的大背景下，结合城市路面信息实时/时变的特性，建立了应急救援物资输送的路径优化模型，并通过改进遗传算法动态调整救援车辆行驶路径保证救援物资输送路径最

短。本文为救援团队提供了更准确、及时的救援方案，有效提高了救援效率。但本研究只适应于确定应急救援物资的输送，并无法满足输送伤员的要求，因为在此类救援方案中，还应道包括伤员的搜救及回送阶段(将伤员送回救援点或者附近医院的过程)，在这方面需要未来更为深入的研究。

参考文献：

[1]2008年十大自然灾害事件[J].中国减灾,2009(1):7-9.

[2]王绍仁,马祖军. 震后随机动态LRP多目标优化模型及算法[J].计算机应用研究,2010,27(9):3283-3286.

[3]王旭坪,李小龙，郭武斌. 基于情景分析的应急路径选择研究[J].运筹于管理,2012(5):67-72.

[4]代颖,马祖军,朱道立,等.震后应急物资配送的模糊动态定位—路径问题[J].管理科学学报,2011,15(7):60-70.

[5]王玮,刘茂,王丽.基于马尔科夫决策过程的应急资源调度方案的动态优化[J].南开大学学报:自然科学版,2010,43(3):18-23.

[6]Alexander D. Towards the development of a standard in emergency planning[J].Disaster Prevention and Management.1005,14(1):158-175.

[7]周定平.突发事件应对的物资保障分析[J].中国安全科学学报,2008,18(3):22-25.

[8]范文璟.城市突发公共事件应急资源调配中出救点选择与救援车辆路径的集成优化研究[D].成都：西南交通大学,2011.

[9]吴瑶.城市突发公共事件伤员救治出救点选择与车辆路径集成优化研究[D].成都：西南交通大学,2011.

[10]王富,李杰,石永辉.城市突发公共事件交通应急组织方法研究[J].交通科技,2013(1):158-160.

[11]代颖,池宏,贾传亮.多路径下应急资源调度的非线性混合整数规划模型[J].运筹与管理,2007,16(5):5-9.

[12]Li D Q. Performance Evaluation research of emergency logistics information system[J]. International Conference on Business Computing and Global Information,2011:167-169.

[13]宋少忠,欧阳涛,赵浩宇.动态数据库功能在B/C结构程序设计中的实现[J].吉林大学学报,2011,49(1):111-117.

[14]Chen H K, Hsueh C F, Chang M S. The real-time time-development vehicle routing problem[J]. Transportation Research Part E: Logistics and Transportaion Review. 2006,41:383-408.

[15]Zhong M H, Shi C, Fu T R. Study in performance analysis of China Urban Emergency Response System based on Petri net[J]. Safety Science. 2010,48:755-761.

[16]赵晓煜,汪定伟.供应链中二级分销网络优化设计的模糊机会约束规划模型[J].控制理论与应用,2001,19(1):149-153.

[17]詹子娜,金龙哲,白楠,等. 基于避险设施的火灾救援及避灾路线算法[J].北京科技大学学报[J].2014,36(7):966-971.

[18]Woensel T V, Peremans H, Vandaele N. A vehicle routing problem with stochastic travel times[J]. European Journal of Operational Research, 2007,144(10):379-396.

宋晨阳，王锋，张韧，等.气候变化背景下我国城市高温热浪的风险分析与评估[J].灾害学, 2016,31(4):201-206.[Song Chenyang,Wang Feng,Zhang Ren, et al.Risk Analysis and Assessment of High-temperature and Heat-wave Disaster in Chinese Cities Under the Background of Climate Change[J].Journal of Catastrophology, 2015,30(4)：201-206.]

Unconventional Emergency Aid Delivery Path Optimization Research

Yan Junai and Guo Yiyuan

(SchoolofManagementScienceandEngineering,ShanxiUniversityof

FinanceandEconomics,Taiyuan030006,China)

Abstract:In view of the sudden and unpredictability of the unconventional emergencies, it needs to determine the path of emergency rescue in time in order to guarantee the effectiveness of the rescue, which will deliver enough aid to the accident spot in the shortest time. According to the severity of the unconventional emergencies, it may need large amounts of emergency relief supplies; however, the relief supplies in the accident spot can not meet the requirement, now it requires multiple relief points to an accident at the same time to carry goods. Therefore, our research is based on real-time/time-varying traffic information under the condition of saving more unconditional emergency relief supplies distribution route optimization problem. In order to achieve the purpose of solving the shortest circuit, the article applied the improved genetic algorithm for dynamic path adjustment. It realizes the dynamic emergency relief supplies path optimization, and provided accurate, timely and visualized rescue plan, and improved the whole effectiveness of relief activities.

Key words:emergency rescue; goods delivery; real-time; time dependent; path optimization; improved genetic algorithm; safety stock

作者简介：阎俊爱(1964-)，女，山西襄汾人，博士，教授，硕士生导师，研究方向为防灾减灾.E-mail：sxyja@126.com

基金项目：2013年山西省软科学课题(2013041010-04)；2015年山西省哲学社会科学规划课题(晋规办[2015]3号)

收稿日期：2015-05-04修回日期：2015-06-16

中图分类号：X43

文献标志码：A

文章编号：1000-811X(2016)01-0193-08

doi:10.3969/j.issn.1000-811X.2016.01.036