基于Hopfield网络的复杂网络社团提取

代婷婷， 梅 端

(1.昭通学院 数学与统计学院， 云南 昭通 657000； 2.广东海洋大学 理学院， 广东 湛江 524088)

●数学研究

基于Hopfield网络的复杂网络社团提取

代婷婷1， 梅 端2

(1.昭通学院 数学与统计学院， 云南 昭通 657000； 2.广东海洋大学 理学院， 广东 湛江 524088)

针对复杂网络中的社团提取问题，提出了一种基于离散Hopfield神经网络的社团结构提取算法，该算法的思想为：首先，对复杂网络数据的进行处理；其次，结合社团提取准则模块度函数Q的形式设计Hopfield神经网络的权值向量W和阈值T；最后，根据网络稳定点的输出值提取出网络中的社团结构.仿真实验表明，本文中的Hopfield神经网络算法比谱分算法得出的Q值更优，对网络的划分更接近实际网络.针对复杂网络中的社团提取问题，提出了一种基于离散Hopfield神经网络的社团结构提取算法，该算法的思想为：首先，对复杂网络数据的进行处理；其次，结合社团提取准则模块度函数Q的形式设计Hopfield神经网络的权值向量W和阈值T；最后，根据网络稳定点的输出值提取出网络中的社团结构.仿真实验表明，文中的离散Hopfield神经网络算法比谱分算法得出的Q值更优，对网络的划分更接近实际网络

复杂网络； 社团提取；Hopfield神经网络

1 引言

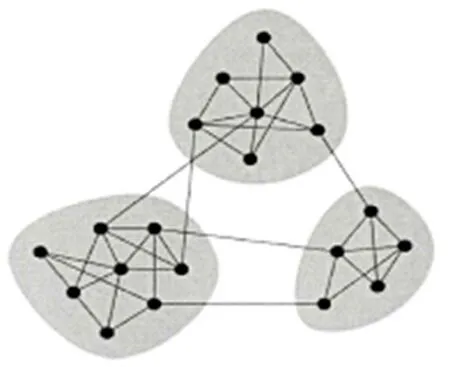
图1 三个社团组成的复杂网络[1]

近些年来，复杂网络吸引了很多领域研究人员的关注，诸如物理学、生物学、社会学、工程等领域的极大关注，因为复杂网一般是指节点众多，连接关系复杂的网络，这是因为这种灵活普通的描述能力，使得它可以用于各学科领域对复杂系统建模、分析.因此，对于复杂网络的研究越来越多.随着对复杂网络的深入研究，发现复杂网络有一些共同特征即它门中都存在社团结构，这些社团的共同特点是外部链接稀疏，内部链接紧密，如图1所示[1-2].事实上，社团结构在实际系统中有着重要的意义：在人际关系网络中，社团结构可能是代表每个家庭、可能是代表某种职业、可能是代表某个地区或者是年龄的群体；在万维网中，不同的社团可能代表了不同的网页[3]；在新陈代谢网络及神经网络中可能代表了某种功能单位；在食物链网中，社团代表了生态系统中的子系统.在研究网络的性质及功能时，社团结构也有相当显著的表现.例如，在网络动力学的研究中，当外加能量处于较低的水平时，同一社团的的个体就能达到同步状态；在网络的演化研究中，相同社团内的个体可能始终连接在一起[4].总之，如果要了解网络结构和功能，那么研究网络中的社团结构是一个很好的途径.因此，用什么样的的方法将网络中的社团结构提取出来表现的相当重要.针对提取出复杂网络中的社团结构这课题，很多研究人员提出了很多的算法，其中最早的就是2003年Newman和Girvan[5]提出的GN算法，继次之后国际上掀起了一股社团提取的热潮，不同领域的科学家提出了很多新颖的方法.

2 算法与理论

2.1 模块度函数[6-8]

针对复杂网络的社团提取，2004年Nweman和Girvan定义了一个量化的社团提取标准——模块度函数Q，每个社团划分的是否合理可以由模块度Q来度量，较合理的划分拥有较高的模块度Q，给定具有n个节点的网络G=(V,E),模块度含义是指落在同一社团内的两个节点实际的边减去这两个节点有边的概率，然后将这些差值相加就是模块度，表达式如下:

(2-1)

m表示网络的总边数，若顶点i,j被划分到一个社团内，则δij=1，否则δij=1，didj表示节点i,j所具有的度，Aij表示网络的邻接矩阵.为了最大化(2-1)，引入决策变量，定义了n维决策变量.引入n维决策向量((x1,x2…x)′∈Rn,其中

则(2-1)就可以用模块度矩阵B表示为：

(2-2)

因此，模块度复杂网络的社团提取问题就变成了数学优化问题：

(2-3)

(2-4)

2.2 基于模块度的谱算法[9]

Gewman和Girvan在2004年定义模块度函数Q时，为了最大化模块度Q，采用的是基于′模块度矩阵的谱算法，通过计算模块度矩阵的最大特征值对应的特征向量来决定决策向量的符号，下面给出此算法的具体步骤：

Step 1:输入复杂网络的邻接矩阵A和度向量d；

Step 3:计算矩阵B的特征值及特征向量；

Step 4：根据最大特征值λmax对应的特征向量umax确定决策向量x的符号，其中

Step5：将决策向量x中+1对应的节点组成的社团P提取出来.

2.3Hopfield神经网络理论[10]

Hopfield网络是由美国加州理工学院物理学家J.J.Hopfield教授于1982年提出的一种单层反馈神经网络，Hopfield网络在输入的激励下，可以得到Hopfield网络的输出，这个输出反馈到输入又会得到新的输出，那么当这个反馈过程已知进行下去，如果Hopfield网络是一个能收敛的稳定网络，则这个反馈与迭代的计算过程所产生的变化就越来越小,一旦达到稳定状态，Hopfield网络就会输出一个稳定的恒值.这就是Hopfield网络的稳定性，也是Hopfield网络在很多领域被广泛应用的基础，而分析Hopfield网络稳定性的工具就是能量函数.

一个n介Hopfield网络H=(W,T)由n个神经元、权值矩阵和阈值向量组成，W=(wij)为n×n阶权矩阵，其元素表示神经元j到神经元i的权重，T=(ti)为n维列向量，称为阈值向量，其元素ti表示神经元i的阈值，网络的输入输出是关于时间t的函数，输入用x(t)=(x1(t),x2(t),x3(t),…,xn(t))′表示，输出用v(t)=(v1(t),v2(t),…,vn(t))′表示，Et是Hopfield网络在t时刻的能量函数，f是激活函数.

依据不同的激活函数，将Hopfield网络分成离散型(DHNN)和连续型(CHNN)两种,在DHNN下的激活函数f的值一般取1，-1或者1,0.DHNN的工作方式一般有同步和异步两种工作方式，我们重点介绍第一种同步工作方式.

DHNN的同步工作方式(并行)

在某一时刻n个神经元同时改变状态，更新方式如下：

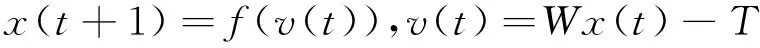
(2-5)

同步能量函数

(2-6)

下面我们介绍一个定理，这是根据设计出的网络权矩阵判断DHNN网络同步工作时是否收敛的依据.

定理：网络以同步方式工作时，若权矩阵 为对称矩阵，那么对于任意初态离散型的Hopfield网络将收敛到一个稳定点或一个长度为2的极限环，即网络收敛的状态满足：

2.4 基于Hopfield神经网社团提取算法

现阶段，Hopfield网络主要是利用渐进稳定点来解决实际问题，将能量函数视为一个优化问题的目标函数，把系统的稳定点作为能量函数的极小点，那么从一个初始状态朝这个稳定点的迭代过程就是求解该优化问题的过程.此方法的优点在于只要构成这种反馈网络，适当的设计其权矩阵和阈值向量就可以达到目的.

本文方法的基本思路：第一步，根据模块度准则设计Hopfield网络的权值向量W和阈值T，同时依据上面提到的定理，保证此网络最终能够收敛；第二步根据复杂网络节点的数目随机生成Hopfield网络的初值，这里的初值首先假定为1和-1，带入设计的 和 中；第三步将以上两步的计算结果带入Hopfield网络的能量函数中进行迭代直到Hopfield网络收敛；第四步，输出Hopfield网络收敛结果x(t)，提取出社团P={vi|xi(t)=+1}.

能量函数稳定点就对应于如下模块度准则的一个局部最优解，其中B为模块度矩阵.

(2-7)

3 实证分析

3.1 数据来源及处理[11]

本文中的实验数据来自复杂网络数据库(Networkdata)，我们可以在网站http://www-personal.umich.edu/～mejn/netdata/下载.本文下载了一些具有代表性的实际复杂网络数据Zachary空手道俱乐部网络，它是一个社会网络，共有34个成员，因为某种意见形成了以校长和主管为代表的两个社团.节点0和33分别代表校长和主管；宽吻海豚网络62个成员，在研究期间由于一个关键成员的离开，海豚群落自然分为两个小的群落，还有美国政治书籍网络、美国大学足球赛网络等.在实验过程中本文所用的工具是Watlab2014.

3.2 实验结果分析

本文中对Zachary空手道俱乐部网络进行了重点实验，利用 2014采用已有的方法和本文提出的方法在Zachary空手道俱乐部网进行了实验，主要是从提取的指标函数值能否达到最优以及当指标函数值达到最优时社团结构方面将本文提出的算法和之前已经有的算法进行了比较.

3.2.1 模块度指标检验Zachary空手道俱乐部网络

使用模块度Q指标对Zachary空手道俱乐部网络进行社团提取，谱算法得到的最大的Q=0.371 5，在此目标函数值下Zachary网络社团划分的结果是唯一的见图2(a)，Hopfield神经网算法得到的 ，在此目标函数取得最优的情况下，Zachary网络的划分结果如图2(b)所示.在Hopfield神经网算法迭代计算的过程中网络收敛稳定时得到的Q值按从大到小的顺序排列，不同的Q值其所对应的频数见表1.

表1 Hopfield神经网算法得到的目标值Q及对应的频数和划分

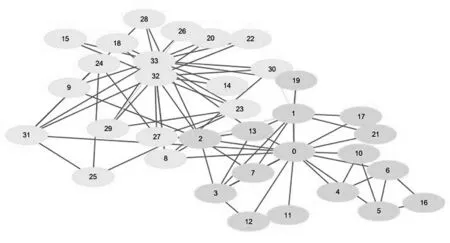
图2(a)

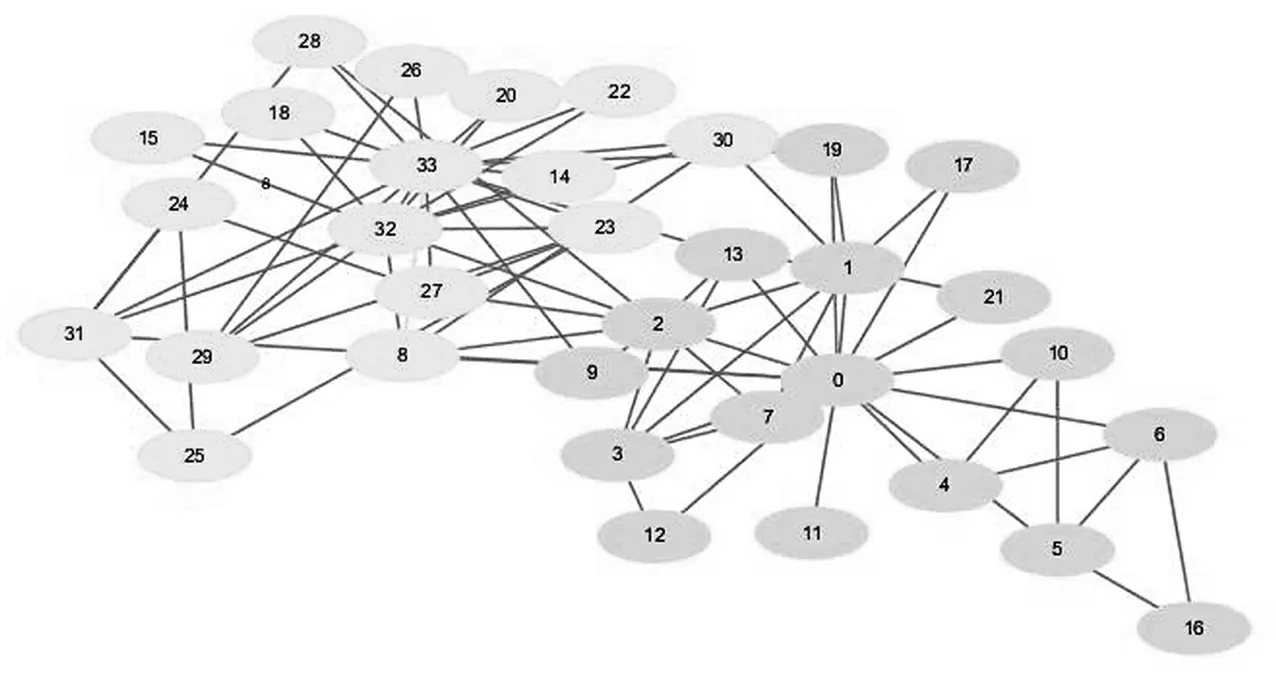
图2(b)图2.Zachary网络在谱分算法和Hopfield方法下划分结果

图2(a)谱算法在Q=0.371 5的网络划分结果,图2(b) Hopfield神经网算法在Q=0.371 8时的划分结果，在Hopfield神经网络算法计算迭代的过程中我们发现Q=0.371 5是该算法的次最大，这时候划分也是相同的.但是Hopfield神经网算法可以得出一个最大的Q=0.371 8，那么在Hopfield神经网算法这两个目标值下所对应的网络状态有什么联系呢？通过实验数据发现，图2(b)是某一初值收敛到极限环的最终状态，而图2(a)就是它的前一个状态，当9号点被划分到另外一个社团后，Hopfield神经网络就稳定了，这两个状态称为极限环的一组对偶解.

3.2.2 模块度指标检验海豚网络

宽吻海豚网络是一个具有62个节点的网络，同样也使用模块度函数Q作为目标函数，分别使用本文的Hopfield神经网络算法和谱分算法对宽吻海豚网络进行划分，随机生成了800个Hopfield网络初值，有85个初值收敛到网络的稳定解，剩下的收敛到了极限环，将Hopfield网络算法得到的模块度函数Q值从小到大进行排序，发现Hopfield网络算法的前5个Q均大于谱分算法的最大的Q值，谱分算法得到的最大Q值是0.385 6具体结果如表2.划分后的可视化图形如图3所示.

表2 Hopfield网络算法在宽吻海豚网络上划分结果

图3 (a)

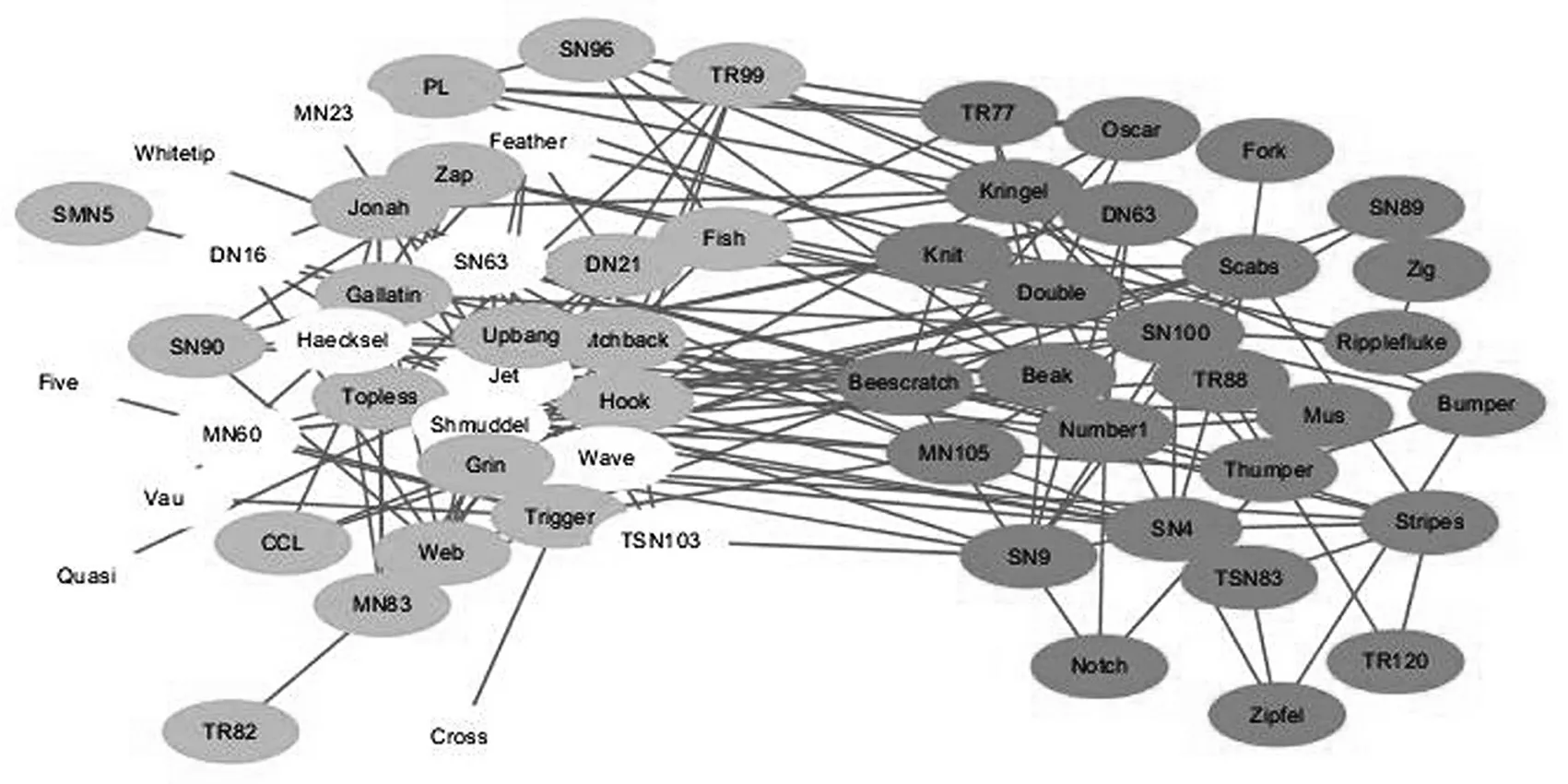
图3 (b)

图3 (c)

图3 (d)

图3 (e)图3.dolphin在Hopfield算法下前5个最大特征值对应的网络划分结果图

注：只列出了Hopfield网络算法前面最大的5个Q值

上面的结果说明了，以模块度函数Q能取得最大的值作为复杂网络社团提取的准则，那么本文的Hopfield网络算法优于其他的算法， 图3(e)的划分结果对应于谱分算法的最优值的划分，但是实际中宽吻海豚网络对应于图3(a)的划分，除此之外，我们在Zachary空手道俱乐部网络上实验时，Hopfield神经网算法可以得出一个最大的Q=0.371 8比谱分算法得到的Q值要大，且对应的划分也比谱分算法得到的划分更接近实际网络，即只要能根据社团提取指标设计出新的Hopfield神经网算法网络矩阵与阈值向量，就可以用它来提取出复杂网络中的社团结构.

4 总结与展望

随着信息技术的产生，数据规模的迅速膨胀，人们现实中的许多复杂系统抽象成许多复杂网络来研究，然而复杂网络是由一些社团构成，而且这些社团的的结构和功能决定和反应的复杂网络的功能特性.因此，如何提取出复杂网络中的社团结构就成了相关领域的研究热点，本文针对这个问题提出了一个新的社团提取算法即Hopfield神经网算法，该方法通过简单的迭代，当网络达到稳定状态能量函数取得最小值时，根据网络的稳定点输出就可以提取出复杂网络中的社团结构简单快速，但是也存在一些不足，即网络的规模超级大的时候，大规模的数据用迭代的方法操作会耗费很长的时间，甚至一般的家用计算机因为配置的原因都无法操作.所以在以后的研究中要进一步的完善该方法，或者设计出更有效的社团提取方法.

[1]S.Fortunato.Communitydetectioningtaphs.Rep[J]. 2010,486(3):75—85.

[2]D.Wats,Sstrogatz.Collectivedynamicsof’small-world’[J].Nature,1998, 393(6):440—442.

[3]A.L.Barabasi,R.Albert.Emergenceofscallinginrandomnetworks[J].Science,1999,286(5439):509—512.

[4]王树禾. 图论[M]. 北京：科学出版社，2009.

[5]M.E.J.Newman.Thestructureandfunctionofcomplexnetworks[J].SIAMReview，2003,45(2):167—256.

[6]Newman.M.E.J.Detectingcommunitystructureinnetworks[J].TheEuropeanPhysicalJournalB:CondensedMatterandcomplexSystems,2004,38(2):321—330.

[7]NewmanM.E.J.modularityandcommunityStructureinnetworks[J].proceedingsoftheNationalAcademyofSciencesoftheUnitedStatesofAmerica,2006,103(23):8577—8582.

[8]Newman.M.E.J.Findingandevaluatingcommunitystructureinnetworks[J].PhysicalReviewE,2004,69(2):026113.

[9]Newman.M.E.J.FindingandevaluatingcommunitystructureinnetworksUsingtheeigenvectorsofmatrices[J].PhysicalReviewE,2006,74(3):036104.

[10]HopfieldJ.J.Neuealnetworksandphysicalsystermswithemergentcollectivecomputationalabilities[J].PreceedingsoftheNationalAcademyofScienceoftheUSA,1982,79:2554—2558.

[11]http://www-personal.umich.edu/～mejn/netdata/.

Based on discrete Hopfield network is a complex network of associations

DAI Ting-ting1， MEI Duan2

(1.School of Mathematics and Statistics, Zhaotong University, Zhaotong 657000， China； 2.College of Science, Guangdong Ocean University, Zhanjiang 524088, China)

For community extraction problem in complex networks, this paper proposes a community structure extraction algorithm based on discrete Hopfield neural network, the algorithm ideas as follows: first, to deal with complex network data; Secondly, combining with community extraction criterion module function design Hopfield neural network, in the form of weight vector and the threshold value; Finally, according to the output value of the stable point to extract the network of community structure. Simulation results show that in this paper, a discrete Hopfield neural network algorithm is better than it is concluded that the value of the spectrum points algorithm, the division of the network closer to the actual network.

Complex network; Associations extract; Hopfield neural network

2016-08-06

代婷婷(1986— )，女，甘肃庆阳人，助教，硕士，主要从事智能计算研究.

O157.5，TP

A

2095-7408(2016)05-0019-08