不可约M矩阵最小特征值的界值

蒋建新， 李艳艳

(文山学院 数学学院, 云南 文山 663000)

●数学研究

不可约M矩阵最小特征值的界值

蒋建新， 李艳艳

(文山学院 数学学院, 云南 文山 663000)

研究了不可约非奇异M矩阵B的最小特征值的界的估计问题，得到了三个新的估计式，理论证明新界提高了文献[3]中的相应结果.

非负矩阵；M矩阵；Hadamard积； 谱半径； 最小特征值

1 预备知识

首先引入一些记号和定义：

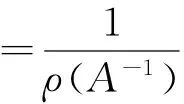
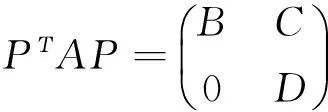
引理1[1]设A,B,C,D∈Rn×n，其中C,D是正对角矩阵，则

引理2[1]设A=(aij)∈Cn×n，则矩阵A的所有特征值都位于下列区域

引理3[1]设A=(aij)∈Cn×n,则A的所有特征值都位于下列区域

引理4[2]设B=(bij)∈Rn×n是行严格对角占优M矩阵，则B-1=(βij)满足

2 主要结果

定理1 设A=(aij)≥0，B=(bij)∈Mn，B-1=(βij)，且A,B都为不可约矩阵，则有

根据引理1有，(FV)-1(A∘B-1)(FV)=(FV)-1A(DU)∘B-1=G∘B-1,即ρ(A∘B-1)=ρ(G∘B-1)=λ，应用引理2知存在i使得

定理2B=(bij)∈Mn，B-1=(bij)，则有

证明： 在定理1中令A=J(矩阵J为元素全为1的矩阵)，则

定理3 设A=(aij)≥0，B=(bij)∈Mn，B-1=(βij)，且A,B都不可约，则

(FV)-1(A∘B-1)(FV)=(FV)-1A(DU)∘B-1=G∘B-1,即ρ(A∘B-1)=ρ(G∘B-1)=λ，由引理3知存在i，j使得

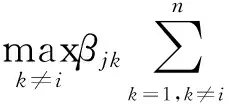
≤pipjβiiβjj(ρ(A)-aii)(ρ(A)-ajj)

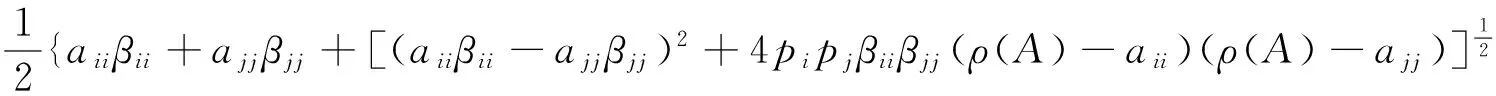
定理4 设B=(bij)∈Mn，B-1=(βij)，则有

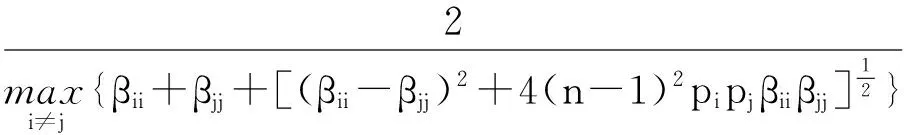
证明： 在定理1中令A=J(矩阵J的元素全为1)，则

推论1 设B=(bij)∈Mn，B-1=(βij)，则有

下面证明推论1提高了文献[3]中的结果.

定理5 设B=(bij)∈Mn，B-1=(βij)，则有

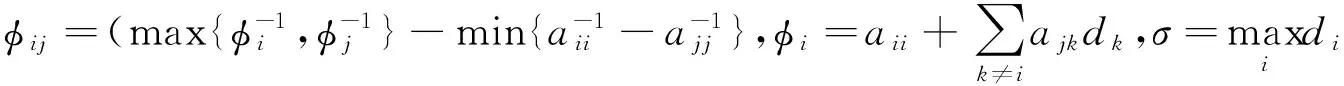
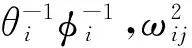
[1]HornRA.JohnsonCR.Matrixanalysis[M].CambridgeUniversityPress,1995.

[2]赵建兴. 矩阵(张量)最小特征值估计及其相关问题研究[D]. 云南大学，2014:8—14.

[3]ChaoqianLi,YaotangLi，RuijuanZhao.Newinequalitiesfortheminimumeigenvalueofmatrices[J].LinearandMultilinearAlgebra, 2013,61(9):1267—1279.

Bound value of the minimum eigenvalues of the irreducible M matrix

JIANG Jian-xin, LI Yan-yan

(School of Mathematics , Wenshan University, Wenshan 663000, China)

Research on the estimation of the minimum eigenvalue of irreducible nonsingular matrix,three new estimators are obtained.Theoretical proof the new bounds have improved thhe result of[3].

nonnegative matrix; matrix; Hadamard product; spectral radius; the minimum eigenvalue

2016-03-08

蒋建新(1981— )，男，甘肃天水人，讲师，硕士，主要从事矩阵理论及其应用研究.

O

A

2095-7408(2016)05-0007-04