基于似无关模型的改进多元损失函数方法

张旭涛， 何 桢， 毕海玲

(1. 军事交通学院 装备保障系，天津 300161; 2. 天津大学 管理与经济学部，天津 300072)

基于似无关模型的改进多元损失函数方法

张旭涛1,2， 何 桢2， 毕海玲1

(1. 军事交通学院 装备保障系，天津 300161; 2. 天津大学 管理与经济学部，天津 300072)

对复杂产品或过程中存在相关性的多响应优化问题进行了研究，通过引入似无关回归模型对质量损失函数方法进行改进，将响应间的相关性综合考虑到模型拟合和参数优化两个阶段。算例表明，与传统质量损失函数方法相比，改进方法得到的最优解处期望质量损失更小。该方法克服了传统方法忽视响应间的相关性或只在优化阶段考虑相关性的不足，是对多元损失函数的重要改进。

似无关回归； 多响应优化； 损失函数； 响应曲面方法； 响应相关性

响应曲面方法[1](response surface methodology, RSM)在产品质量改进或过程优化中有着广泛的应用。现实中产品和过程的多个质量特性往往是相互影响的，响应变量间存在着相关性。当响应变量间相关性较强时，会对模型拟合的精度和优化结果的可靠性产生较大影响。损失函数法是处理响应间存在相关性时建立多响应优化函数的经典方法。但该方法只是在构建多响应优化目标函数时考虑了响应间的相关性，在拟合响应回归模型和考虑预测误差时仍是基于最小二乘(ordinary least squares, OLS)方法，一定程度上忽略了响应间的相关性。鉴于此，通过引入似无关回归模型[2](seemingly unrelated regressions, SUR)对传统的质量损失函数方法进行改进，一方面在度量目标偏离损失时采用更精确的SUR预测模型，另一方面在考虑响应的预测误差时引入了响应误差项的方差协方差阵，更充分地利用了响应间的相关性信息。给出了改进损失函数方法的具体步骤和算例说明，并将结果与经典方法进行对比，验证其有效性。

1 相关研究评述

1.1 损失函数方法

多元质量损失函数最初由Pignatiello[3]在田口单响应质量损失函数的基础上提出：

L=[y(x)-θ]TC[y(x)-θ]。

(1)

其中y(x)为在某位置x处的响应值向量，C是一个表示过程经济性的正定常数矩阵，θ为最优目标响应值向量。质量损失L的期望函数为

E(L)=[E[y(x)]-θ]TC[E[y(x)]-θ]+trace[C∑y(x)]。

(2)

式中，trace表示矩阵的迹，∑y(x)为位置x处响应的方差协方差阵。

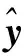
(3)

则质量损失L的期望函数为

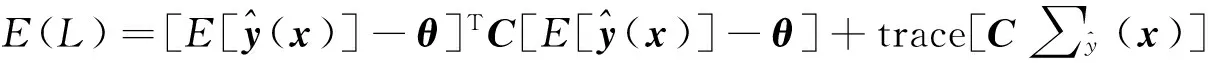
(4)

(5)

实际上，当试验区域内不同位置噪声因子对系统误差影响相同时，trace[C∑y(x)]项是一个固定的常量，则对式(5)的优化可以简化为对式(4)的优化。

在上述3种经典的损失函数法基础上，近年来又有很多关于损失函数的理论和案例研究。如Ouyang等[6]提出了一种考虑模型不确定性的加权质量损失函数法，汪建均等[7]提出在小样本情况时应使用多变量偏最小二乘回归模型，Yadav等[8]和何桢等[9]在损失函数法基础上进一步考虑稳健性，Sibalija等[10]给出了质量损失函数法在激光钻孔的多响应参数优化的应用等。

1.2 SUR回归模型

考虑有r个响应y1,y2,…,yr的多响应问题，每个响应均有n个观测值，第i个响应对应模型的矩阵表示为

yi=Xiβi+εi,i=1,2,…,r。

(6)

式中yi为第i个响应的n×1观测值向量，Xi为n×pi数据矩阵，βi为pi×1待估计系数向量，εi为随机误差向量。

传统RSM方法一般假设不同响应间的误差项是相互独立的，即Cov(εi,εj)=0，回归系数估计采用最小二乘估计:

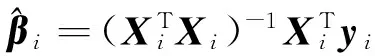
(7)

估计系数的方差协方差阵为

(8)

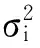
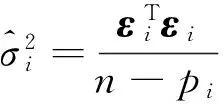
(9)

式中εi又可视为第i个响应的OLS回归残差，n-pi为残差的自由度。

对于式(6)表示的r个响应的模型，如果假设每个模型的误差项是独立同分布的，但模型之间的误差项是相关的，则称这样的模型为似无关模型，即

(10)

将式(6)表示的r个响应的SUR模型写成矩阵形式为

Y=Xβ+ε。

(11)

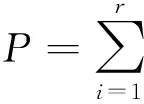
(12)

式中⊗为Kronecker乘积符号，∑为响应间误差项的方差协方差阵，记为∑=(σij)，即

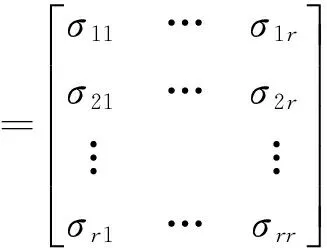
(13)

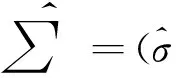
(14)

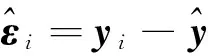
与OLS方法对各个响应模型分别独立估计不同，SUR方法将多响应模型作为整体进行估计，充分利用了样本和误差项的信息，通常能给出更精确的模型参数估计。从式(14)可知，SUR回归需要以OLS回归为基础来估计响应间误差项的方差协方差阵。

近年来有学者尝试将SUR模型应用到多响应曲面优化中来，Shah等[11]指出当响应间相关性较强时，基于SUR模型优化时堆叠等值线图上可以获得更大的可行域。Peterson等[12]研究了基于SUR模型的多响应优化的贝叶斯方法，但该方法属于概率方法，无法定量给出各个响应的具体优化情况。

2 基于SUR模型的改进多元损失函数方法

下面以Vining方法为例，基于SUR模型对模型拟合阶段和优化阶段对该方法进行改进，并进行结果对比，其思路同样适用于其他损失函数方法的改进。基本步骤如下。

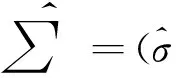
2)将试验观测数据写成式(11)所示的SUR模型形式，利用式(12)得到多响应SUR回归模型系数矩阵的估计，估计系数的协方差为

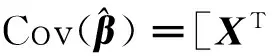
(15)

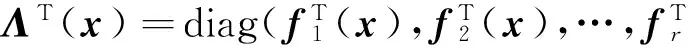
(16)

预测响应的方差协方差为

(17)

3)将式(16)和式(17)分别替换式(4)中对应的估计项，有

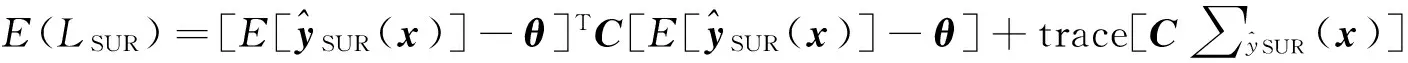
(18)

4)选择成本矩阵C。在质量损失函数中，过程经济性和响应间的相关性可以通过成本矩阵C来考虑。Vining[4]对成本矩阵如何选择进行了讨论，并给出了3种定量选择的方法。由于本文关注的是SUR和OLS两种不同数据处理思路对优化结果的影响，成本矩阵C的讨论不是本文的重点，在应用中可以根据实际情况灵活选取，本文在算例分析中进行结果对比时，成本矩阵C采用对比文献中的相同设置值。

5) 在试验的设置区域内进行对式(18)进行最小值优化。由于目标函数比较复杂，比较可行的方法是采用智能算法如遗传算法。 初始可行解可以通过堆叠等值线的方法获得，由于遗传算法是一种随机搜索算法，对于较复杂的优化问题，每次得到的结果可能会有细微差异，因此在实际应用时需要重复运行该算法，以得到尽可能多的最优点以供决策者参考。

3 算例

算例采用文献[4]中引用的一个聚合物试验，试验数据如表1所示，表中的因子水平已编码。试验的目的是为了确定反应时间(x1)、反应温度(x2)和催化剂用量(x3)的参数设定值，使得聚合物转化率(y1)最大，且热力学活性(y2)达到目标值57.5。聚合物转化率的可接受范围为80～100，热力学活性的可接受范围为55～60，故目标值可以分别设为θ1=100，θ2=57.5。

表1 聚合物试验数据Tab.1 The experiment results for the polymer experiment

基于OLS拟合出各个响应的曲面方程：

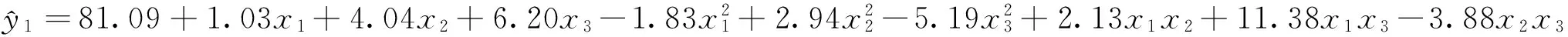
通过式(8)可以得到基于OLS的响应y1方程估计系数的方差-协方差阵，如表2所示。

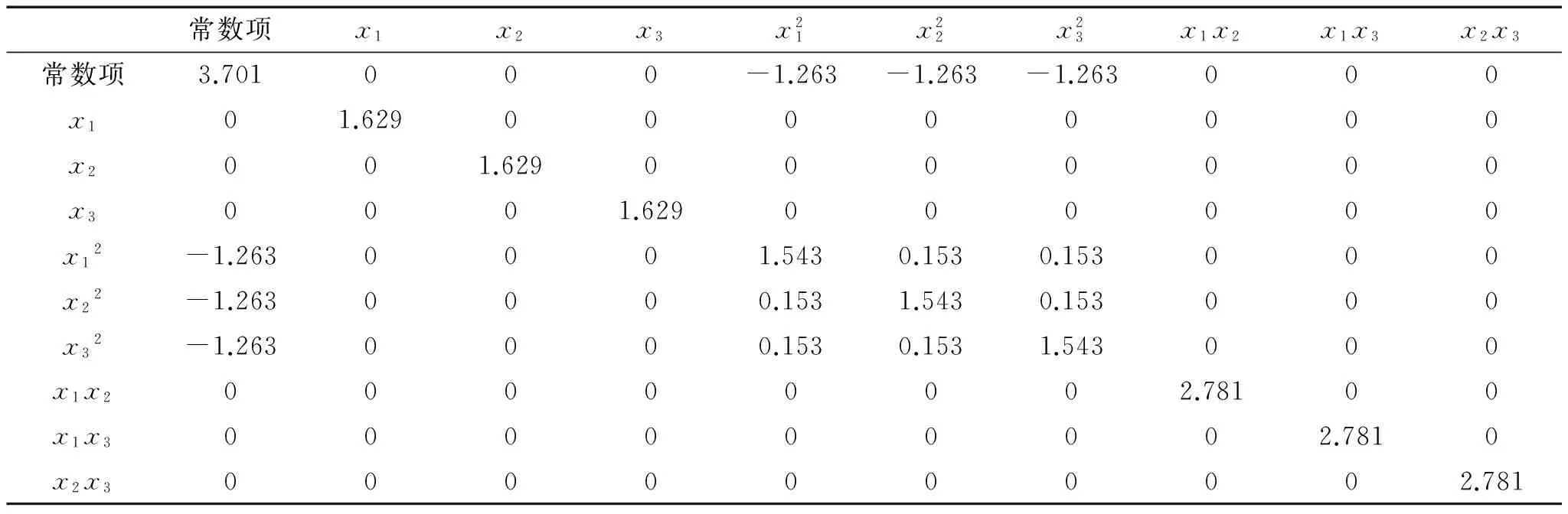
表2 基于OLS的响应y1方程估计系数的方差-协方差阵Tab.2 Variance-covariance matrix for parameters for y1 using OLS

利用OLS残差通过式(13)给出预测响应误差项的协方差阵的极大似然估计为

采用SUR模型估计的响应曲面模型为

可以看出，用两种回归方法得到的响应y1的模型系数结果有差别。

利用式(15)可以得到基于SUR的响应y1方程估计系数的方差-协方差阵，如表3所示。

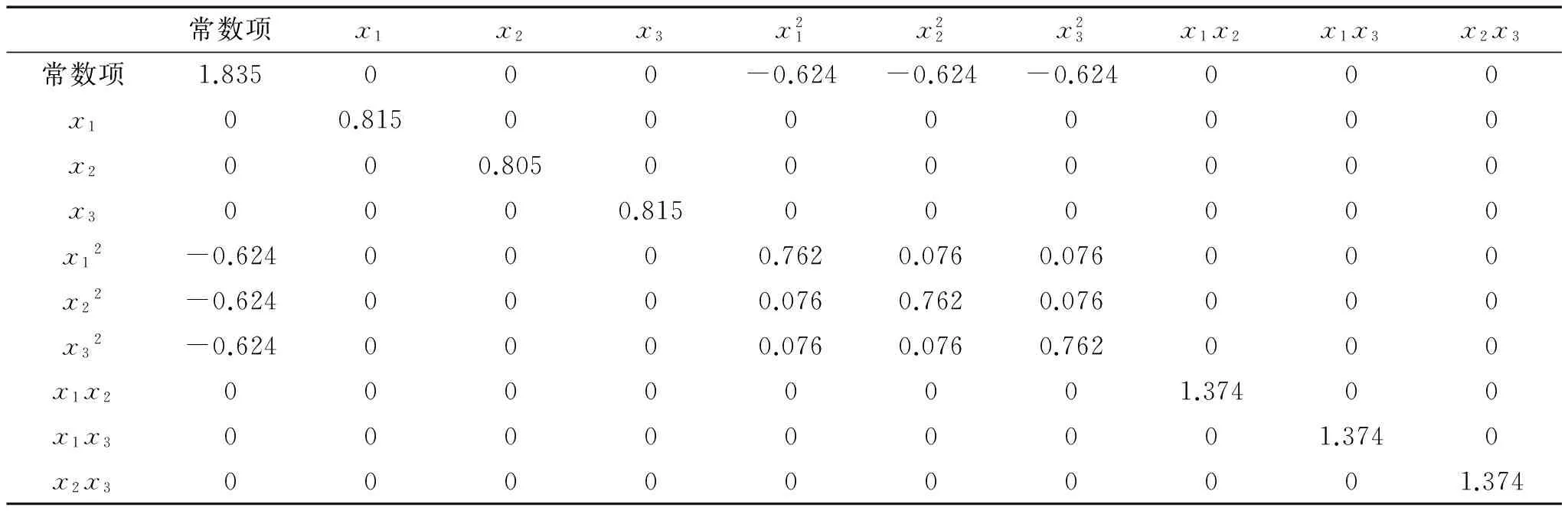
表3 基于SUR的响应y1方程估计系数的方差-协方差阵Tab.3 Variance-covariance matrix for parameters for y1 using SUR

对比表2和表3可以看出，表3中的非0项绝对值均比表2中的小，意味着采用SUR方法得到响应y1的模型拟合精度更高。

为了与文献[4]中基于OLS的Vining质量损失函数法进行结果对比，成本矩阵C采用文献[4]中相同的设置值，即：

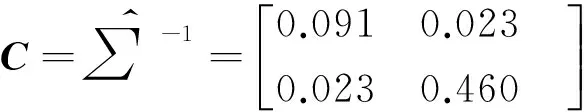
表4 本文方法与Vining方法优化结果对比Tab.4 Comparison of optimization results between the proposed approach and Vining’s method

4 结论

响应间的相关性会对基于RSM的多响应优化方法中的模型拟合和优化结果产生影响。通过引入SUR模型对质量损失函数方法进行改进，将响应间的相关性综合考虑到模型拟合和参数优化两个阶段中，是多响应优化方法的重要补充。在与传统方法进行对比分析的算例中，改进方法能找到更好的最优解。研究只考虑了模型拟合精度和预测误差对优化结果的影响，实际过程中噪声因子或可控因子波动会引起响应的波动，后续研究可以在此基础上进一步考虑多响应间存在相关性时基于SUR的稳健性参数优化问题。

[1]ARDAKANIMK,WULFFSS.Anoverviewofoptimizationformulationsformultiresponsesurfaceproblems[J].QualityandReliabilityEngineeringInternational, 2013, 29(1): 3-16.

[2]ZELLNERA.Anefficientmethodofestimatingseeminglyunrelatedregressionsandtestsforaggregationbias[J].JournaloftheAmericanStatisticalAssociation, 1962, 57(298): 266-286.

[3]PIGNATIELLOJJ.Strategiesforrobustmutiresponsequalityengineering[J].IIETransactions, 1993, 25(3): 5-15.

[4]VININGGG.Acompromiseapproachtomultiresponseoptimization[J].JournalofQualityTechnology, 1998, 30(4): 309.

[5]KOY,KIMK,JUNC.Anewlossfunction-basedmethodformultiresponseoptimization[J].JournalofQualityTechnology, 2005, 37(1): 50-59.

[6]OUYANGL,MAY,BYUNJ.Anintegrativelossfunctionapproachtomulti-responseoptimization[J].QualityandReliabilityEngineeringInternational, 2013, 31(2): 193-204.

[7]汪建均，马义中，翟云焕. 相关多质量特性的优化设计 [J]. 管理工程学报, 2011, 25(2): 66-73.

WANGJJ,MAYZ,ZHAIYH.Optimizationdesignofcorrelatedmultiplequalitycharacteristics[J].JournalofIndustrialEngineeringandEngineeringManagement, 2011, 25(2): 66-73.

[8]YADAVOP,BHAMARESS,RATHOREA.Reliability-basedrobustdesignoptimization:amulti-objectiveframeworkusinghybridqualitylossfunction[J].QualityandReliabilityEngineeringInternational, 2010, 26(1): 27-41.

[9]何桢，吕海利. 多元质量特性稳健性设计方法的优化研究 [J]. 管理科学. 2007, 20(1): 2-7.

HEZ,LYUH.Optimizationresearchonrobustdesignwithmultiplequalitycharacteristics[J].JournalofManagementSciences, 2007, 20(1): 2-7.

[10]SIBALIJATV,MAJSTOROVICVD.Multi-responseoptimisationofthermosoniccopperwire-bondingprocesswithcorrelatedresponses[J].TheInternationalJournalofAdvancedManufacturingTechnology, 2009, 42(3-4): 363-371.

[11]SHAHHK,MONTGOMERYDC,CARLYLEWM.Responsesurfacemodelingandoptimizationinmultiresponseexperimentsusingseeminglyunrelatedregressions[J].QualityEngineering, 2004, 16(3): 387-397.

[12]PETERSONJJ,MIRO-QUESADAG,DELCASTILLOE.ABayesianreliabilityapproachtomultipleresponseoptimizationwithseeminglyunrelatedregressionmodels[J].QualityTechnologyandQuantitativeManagement, 2009, 6(4): 353-369.

An Improved Loss Function Approach for Multi-response Optimization Using Seemingly Unrelated Regressions

ZHANG Xutao1,2，HE Zhen2, BI Hailing1

(1. Department of Equipment Support, Military Transportation University, Tianjin 300161, China;2. College of Management and Economics, Tianjin University, Tianjin 300072, China)

Multi-response optimization with correlated responses in complex product or process is studied. The seemingly unrelated regression method is employed to improve traditional loss function approach. Correlations among responses are considered both in the model fitting phase and in the optimization phase. Illustrated example shows that the proposed approach can lead to an optimal solution with smaller expected quality loss. The approach overcomes the drawback of traditional method which ignores the correlation or only considers the correlation in the optimization phase. It is an important improvement on the conventional loss function method.

seemingly unrelated regressions; multi-response optimization; loss function; response surface methodology; correlations among responses

2015- 10- 16

国家自然科学基金委杰出青年基金资助项目(71225006)

张旭涛(1981-)，男，河南省人， 讲师， 博士，主要研究方向为质量管理、试验设计等.

10.3969/j.issn.1007- 7375.2016.06.008

F406.3

A

1007-7375(2016)06- 0051- 05