求解混合约束极大极小问题的精确光滑罚函数法
2016-02-24姜合峰王福胜
姜合峰,高 娟,张 瑞,王福胜
(太原师范学院数学系,山西晋中030619)
求解混合约束极大极小问题的精确光滑罚函数法
姜合峰,高 娟,张 瑞,王福胜
(太原师范学院数学系,山西晋中030619)
提出一个新的精确光滑罚函数法求解混合约束极大极小问题,通过引入一个新变量,将带混合约束的极大极小问题转化为等价的无约束优化问题,证明在合理的假设条件下,罚问题的极小点就是原问题的极小点,数值实验表明新算法是求解带混合约束的极大极小问题的一种有效算法.
混合约束的极大极小问题;无约束优化问题;精确罚函数
0 引言
极大极小问题是一类有广泛应用背景的优化问题,例如:大量的金融、工程管理、经济问题都是转化成极大极小问题模型来求解的.
本文研究如下带混合约束的极大极小问题:

其中,fi:Rn→R,i∈Q,Fi:Rn→R,i∈Igi:Rn→R,i∈K,(Q={1,…,q},I={q+1,…,m},
K={m+1,…,k})是连续可微的函数.由于极大函数是不可微的,所以问题(P)是典型的不可微优化问题,求解极大极小问题有一定的难度.
目前已有多种不同的算法来求解混合约束极大极小问题,如文献[1]结合罚函数和非单调线性搜索技术,并利用SQP方法求解混合约束极大极小问题;文献[2]主要研究混合约束的极大极小问题,它是文献[3]的推广,但通过求解线性方程组获得高阶修正方向;文献[4]将光滑优化问题的积极集约束识别技术推广应用于非光滑的带约束极大极小问题.
近来,在文献[5]和[6]中,分别对于带等式约束和不等式约束的极大极小问题,通过引入一个新的变量,提出了一种新的精确罚函数来求解约束优化问题.受到文献[5,6]的启发,本文考虑带混合约束的极大极小问题,提出了一种新的求解问题(P)的精确罚函数方法.
1 简单精确光滑罚函数
我们引进参量z,则原问题(P)可转化为连续非线性规划问题:

也就是说,求解带混合约束极大极小问题(P)相当于求解问题(¯p).
定义集合:S={(x,z)∈Rn+1:fi(x)-z≤0,∀i∈Q;Fi(x)=0,∀i∈I;gi(x)≤0,∀i∈}K,
则非线性规划问题(¯p)等价于下面的优化问题:
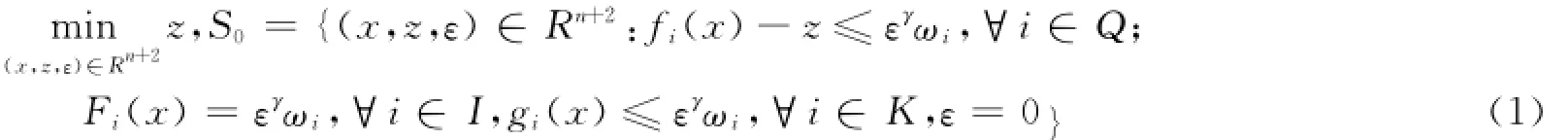
其中,ωi∈(0,1),i=1,2,…k.类似地,定义集合Sε:Sε={(x,z,ε)∈Rn+2:

下面讨论罚函数fσ(x,z,ε)的连续可微性.

2 算法
步2利用BFGS算法求解问题(Pσ),将其解记作(xσ,zσ,εσ).
步3若|εσ|≤ε~,‖▽(x,z,ε)fσ(x,z,ε)‖≤η,则停止,否则,令σ=σ+ρ,转步2.
下面讨论在弱的条件下,此算法中罚问题的极小点就是混合约束极大极小问题的极小点.
引理1 设(xk,zk,εk)∈L(Pσk),且目标函数值fσk(xk,zk,εk)有限和εk≠0,则有(xk,zk,εk)∉Sσk.
定理2 设(xk,zk,εk)∈L(Pσk)且目标函数值fσk(xk,zk,εk)有限和εk≠0,(xk,zk,εk)→
(x*,z*,ε*),且▽Fi(x*),i∈I是线性独立的,约束优化问题(1)在点x*处满足EMFCQ约束规格,那么ε*=0,(x*,z*)∈S.
1)证明ε*=0.由εk≠0和引理1得,(xk,zk,εk)∉Sε.再由(xk,zk,εk)∈L(Pσk),可得



3 数值实验
为了验证算法的可实施性和有效性,本节选取下面两个问题进行数值实验,所有实验均在Matlab R2014a软件编程下运行.
例1[7]minmax{fi(x):i=1,2,3},s.t.f4(x)=x1+x2-2=0,f5(x)=-x21-x22+2.25≤0其中f(x):f1(x)=x21+x22,f2(x)=(2-x1)2+(2-x2)2,f3(x)=2exp(-x1+x2).取初始点为x0=[3,2],最优解为x*=(1.353 6,0.646 4),最优值为2.250 0.参数设置为


表1 例1的数值结果
4 结论
本文针对带混合约束的极大极小规划问题,提供了一种新的求解非光滑的极大极小问题的罚函数法,此罚函数中参数比较多,在算法设计时需对参数进行调整,数值结果表明,不要求很大的罚参数就可以获得问题的最优值点,验证了本文设计的罚函数运算效果良好.
[1]YU Y H,GAO L,Nonmonotone line search for monstrainedminimax problems[J].Journal of Optimization Theory and Application,2002,115(2):419-446
[2]JIAN J B,ZHANG X L,MA R Q.Generalized monotone line search SQP algorithm for constrained minimax problems[J].Optimization,2009,58(1):101-131
[3]JIAN J B,MA R Q,ZHANG X L.Feasible generalized monotone line search SQP algorithm for nonlinear minimax problems with inequality constraints[J].Journal of Computational and Applied Mathematics,2007,205:406-429
[4]D.L.Han,J.B.Jian,J.Li,On the accurate identification of active set for constrained minimax problems[J].Nonlinear Analysis:Theoty,Methods and Application,2011,74:3022-3032
[5]马 骋,李 讯,姚家晖,等.一种新的求解带约束的有限极大极小问题的精确罚函数[J].应用数学和力学,2012,33(2):251-264
[6]郑芳英.求解不等式约束极大极小值问题的罚函数方法[J].浙江理工大学学报,2014,31(5):560-564
[7]唐焕文,张立卫,王云诚.一般约束极大极小问题的一个有效的近似解法[J].经济数学,1995,12(1):10-16
[8]简金宝,光滑约束优化快速算法——理论分析与数值实验[M].北京:科学出版社,2010
A Exact and Smooth Penalty Function for Solving Mixed Constrained Min-Max Problems
JIANG Hefeng,GAO Juan,ZHANG Rui,WANG Fusheng
(Department of Mathematics,Taiyuan Normal University,Jinzhong 030619,China)
A new exact and smooth penalty function was introduced to solve min-max problem of equality and inequality constraints.Though adding a new variable,the mixed constraints min-max problem is transformed to equivalent unconstrained optimization problem.It is proved that,under certain reasonable assumptions,the minimum point of unconstrained optimization problem was equivalent to the minimum point of the original constrained one.The numerical results demonstrate that the new method is an effective approach for solving mixed constrained min-max problems.
mixed constrained min-max problem;unconstrained optimization problem;exact penalty function
1672-2027(2016)04-0041-04
O221.2
A
2016-06-08
姜合峰(1973-),男,山西夏县人,硕士,太原师范学院数学系副教授,主要从事最优化理论与方法.
