机器人镗孔加工系统稳定性分析
2016-02-24方强李超费少华孟涛
方强, 李超, 费少华, 孟涛
1. 浙江大学 机械工程学院, 杭州 310027 2. 中国人民解放军驻西飞公司军事代表室, 西安 710089
机器人镗孔加工系统稳定性分析
方强1,*, 李超1, 费少华1, 孟涛2
1. 浙江大学 机械工程学院, 杭州 310027 2. 中国人民解放军驻西飞公司军事代表室, 西安 710089
为了解决大型飞机装配现场主起落架交点孔的镗孔精加工问题,提出了采用六自由度工业机器人及专用末端执行器组合的创新解决方案。压脚是抑制机器人镗孔加工系统颤振的核心环节。通过对施加压脚前后的机器人镗孔加工系统进行动力学建模,对系统的稳定性进行分析,得出压脚装置对加工系统稳定性叶瓣图的影响。最后通过实际镗孔加工实验验证了机器人镗孔系统在不同压脚压力下的加工稳定性,表明合理的压脚压力可提高稳定切深,拓展加工稳定区域,有效避免加工颤振。
压脚; 工业机器人; 镗孔; 颤振; 稳定性叶瓣图
近30年,工业机器人经历了从仅能完成单一重复性指定任务朝着可编程、多任务的方向发展,但80%的工业机器人的应用仍停留在传统的焊接、搬运等对运动精度要求不高的领域。随着波音、空客等航空企业将机器人成功应用于要求高精度的自动化制孔系统,国内外航空制造企业纷纷开始研究相关技术[1-2]。然而由于机器人自身刚度不足导致使用中颤振影响较大,这大大抑制了工业机器人在孔加工中的应用[3]。对于颤振的研究,目前运用较多的有再生颤振原理、振型耦合颤振原理、负摩擦自振原理3种理论[4]。Özer和Semercigil[5]将分析机床颤振用的传统的再生颤振理论用于机器人铣削加工中,从单自由度理论分析机器人铣削加工,对颤振从两个角度进行半主动控制,一个是改变切深,另一个是改变机器人的姿态角,也即改变其刚度,取得了较好的控制效果;Pan等[6]结合对机器人铣削过程中大量的实验现象观察,发现由于工业机器人各向低刚度的特性,铣削过程中存在耦合颤振现象。同时理论分析和实验验证了切深稳定准则,但没有深入分析稳定条件,只是定性说明了各向刚度之间的关系对系统稳定性的影响。在机器人制孔系统中,压脚装置是保证其加工稳定性的一项关键技术。美国Electroimpact、柯马、德国宝捷等公司研发的机器人制孔设备上,都采用了压脚装置[7-8]。机器人制孔加工过程中,压脚伸出并压紧工件,有3个作用:①消除叠层材料层与层的间隙,减小层间加工切屑和毛刺的产生;②增加系统的动态刚度,加强系统制孔过程的稳定性;③利用压脚轴光栅位置反馈,确保进给轴和加工件相对位置不变,减小加工孔窝深精度误差[9]。Olsson等[10]利用机器人制孔系统末端执行器压脚上3个均匀分布的力传感器的压力和扭矩信号,传递给机器人控制器进行压脚接触力控制,抑制制孔过程中末端执行器相对工件的滑动和振动。王珉和薛少丁[11]利用有限元方法分析了飞机装配制孔中施加单向压紧力对钻削毛刺的影响,以及贴合面间隙随压紧力变化的情况。
本文针对某大型飞机主起落架交点孔的装配现场精加工问题,提出机器人与末端执行器组合进行精镗孔加工的解决方案。利用末端执行器上的压脚装置并合理选择加工工艺参数,解决由于机器人弱刚性引发的颤振问题。以此为背景,深入分析了压脚对于机器人镗孔加工稳定性的影响作用。首先建立包含气动压脚在内的机器人镗孔系统动力学模型,然后在其基础上利用再生颤振原理绘制出稳定性叶瓣图,最后进行了实验验证。
1 机器人镗孔加工系统
1.1 加工对象
根据某大型飞机中机身段装配工艺,主起落架交点框带余量进行装配。在整个中机身段装配完成后,需要对主起落架交点孔进行一次精加工,用以消除制造安装误差。通过工艺补偿达到相互协调,满足机身两侧主起落架交点孔的同轴度和对称性要求。
如图1所示,飞机数字化装配技术利用三坐标数控定位器对飞机部件进行入位调姿,可以满足不同型号飞机的柔性化装配任务[12-13]。若采用传统固定安装在现场的精加工台来完成所有交点孔的精加工任务,不仅成本较高、建设周期长,而且无法适应在飞机数字化装配背景下加工对象在现场位置的改变。工业机器人与特殊设计的镗孔末端执行器组合而成的柔性装备,为解决此种环境下的加工问题提供了一种新思路。

图1 飞机主起落架交点孔加工系统
Fig. 1 Aircraft main landing gear junction hole processing system
1.2 系统构建
机器人镗孔加工系统如图2所示,主要由工业机器人、镗孔末端执行器、激光跟踪仪、机器人离线编程及仿真系统、机器人控制系统等组成。
机器人镗孔系统工作过程为:①通过激光跟踪仪建站测量,得到机器人与工件的坐标关系并建立仿真模型;②利用机器人离线编程及仿真系统从产品数模中提取加工孔信息,按照镗孔工艺要求生成机器人镗孔程序;③利用DELMIA软件对镗孔加工过程进行动画仿真以及机器人的运动轨迹规划,防止加工过程中系统干涉;④机器人控制系统加载程序对机器人进行运动控制,最终完成机器人镗孔加工。

图2 机器人镗孔加工系统
Fig. 2 Robot boring system
1.3 末端执行器
末端执行器是机器人镗孔加工系统的核心部件,如图3所示,由电主轴、进给系统、压脚、刀具系统等组成,通过快换接头与机器人相连。镗孔过程由主轴的旋转运动和进给轴的进给运动两部分组成。
气动压脚作用于镗孔所在部位,主要包括压脚支架、驱动气缸和压脚鼻端等结构。压脚鼻端通过两侧压脚支架连接至压脚气缸,由气缸同步推动,实现前后平移运动并具备保压功能。

图3 末端执行器结构
Fig. 3 End effector structure
2 加工系统动力学建模
2.1 系统模型
机器人镗孔系统结构示意图如图4所示,它包含了工业机器人、末端执行器、压脚气缸、工件以及控制压脚动作的气动回路。其中x、y分别为坐标轴,F为施加在末端执行器上的镗削力。

图4 机器人镗孔系统结构示意图
Fig. 4 Structure diagram of robot boring system
假设被加工件双叉耳孔刚性良好,将其当作一个固定刚体。两个压脚气缸固定于机器人末端执行器底座上。镗孔加工时,压缩气体由气源经储气罐通过比例减压阀调压后,经过一系列气动元件送到驱动气缸的无杆腔内,此时有杆腔与大气连通,从而使得压脚能够对工件保持一定的压紧力。电磁换向阀用于供气气路的切换,控制压脚杆的伸出与缩回。两个节流阀分别用于调节气缸进气和出气的气体流量,同时增大整个气动系统的阻尼比。分流器用于将单路气体分成两路,分别连接至两个气缸。
利用机器人进行镗孔时,切削力通过刀具-主轴-进给丝杠副传递至机器人本体上。数控机床通常具有大于50 N/μm的刚度和1 000 Hz的固有频率,六自由度关节型工业机器人的刚度的数量级仅为1 N/μm,固有频率仅在数十赫兹左右,因此机器人成为整个加工环节中最薄弱的部分。
假设工件为刚性体,由图4可进一步抽象出图5所示的压脚作用下机器人镗孔系统进给方向上的动力学模型图。其中M、K、C分别为机器人及末端执行器在某一确定姿态角下的模态质量、刚度和阻尼参数,Fx为施加在末端执行器上的镗削力沿进给方向x上的分量。
压脚作用下的机器人镗孔系统由两部分组成:一是机器人连同末端执行器,二是气动压脚。工作时气缸左腔接高压气源,右腔直连大气,压脚伸出压紧工件。气动压脚将镗孔机器人由开链机构变为闭链机构。在垂直于进给方向的加工平面内y方向上,仅将系统考虑为单自由度质量-弹簧-阻尼系统。

图5 机器人镗孔系统进给方向上的动力学模型
Fig. 5 Dynamic model of robot boring system in feed direction
2.2 固定姿态下机器人建模
由于六自由度关节型串联机器人的末端动力学特性与其关节姿态角有关,而使用机器人进行镗孔加工时,通常机器人保持固定姿态。因此通过建立质量-弹簧-阻尼系统分别描述机器人在进给方向x和垂直于进给方向的加工平面y方向的动力学特性。
六自由度关节型串联工业机器人的传统静刚度模型为[14]
K=J-TKqJ-1
(1)
式中:关节刚度矩阵Kq=diag(kq1,kq2,…,kq6),kqi为机器人第i(i=1,2,…,6)个关节的等效关节刚度值。在某一确定机器人姿态下,根据机器人6个关节姿态角,计算出其相应位姿下的雅克比矩阵J,得到的刚度矩阵为6×6的方阵,由于刚度矩阵内元素具有不同的量纲,参照文献[15]将该矩阵划分为4个对称部分,得到
(2)
式中:Kfd为力-线位移刚度矩阵;Kfδ为力-角位移刚度矩阵;Kmd为力矩-线位移刚度矩阵;Kmδ为力矩-角位移刚度矩阵。则有
f=Kfdd
(3)
式中:f为末端力矢量;d为末端移动变形。由于Kfd为一个3×3的矩阵,可知机器人末端力-位移之间存在耦合。为了得到机器人在某方向上的刚度,作如下处理:记方向向量e=[exeyez]T,ex、ey、ez为方向向量e在x、y、z方向上的投影值。则末端力矢量可表示为力矢量的模f0和方向向量e乘积的形式
f=f0e
(4)
由式(3)和式(4)得到
(5)
通过式(5)计算得到机器人末端在f作用下的变形向量d,将向量d投影至末端力矢量的方向向量e上,利用向量投影的点积运算规则,得到在力矢量f上发生的变形
df=[exeyez]·d=
(6)
据此可得到在力矢量f上机器人末端的刚度为
(7)
利用文献[16]提出的六自由度关节型机器人关节刚度辨识方法,辨识出实验用机器人ABBIRB6600型各关节刚度值,在最终确定的实验现场机器人加工位姿下(见表1),根据式(1)~式(2)计算得到机器人在进给方向x上的刚度为kx=1.307×106N/m,垂直于进给方向y方向上的刚度为ky=1.128×106N/m。
最后,利用锤击法[17]对该机器人系统进行锤击实验,测得在表1所示机器人姿态下(其中θi为机器人第i(i=1,2,…,6)个关节的角度值),机器人第1阶固有频率为7Hz,故取机器人固有频率ωnx=ωny=7Hz,机器人的阻尼比取ζ=0.02。由此可计算得到机器人在x、y两个方向上的模态参数表2所示。

表1 镗孔加工位姿关节角

表2 机器人镗孔系统模态参数
2.3 包含气动压脚的机器人镗孔系统建模
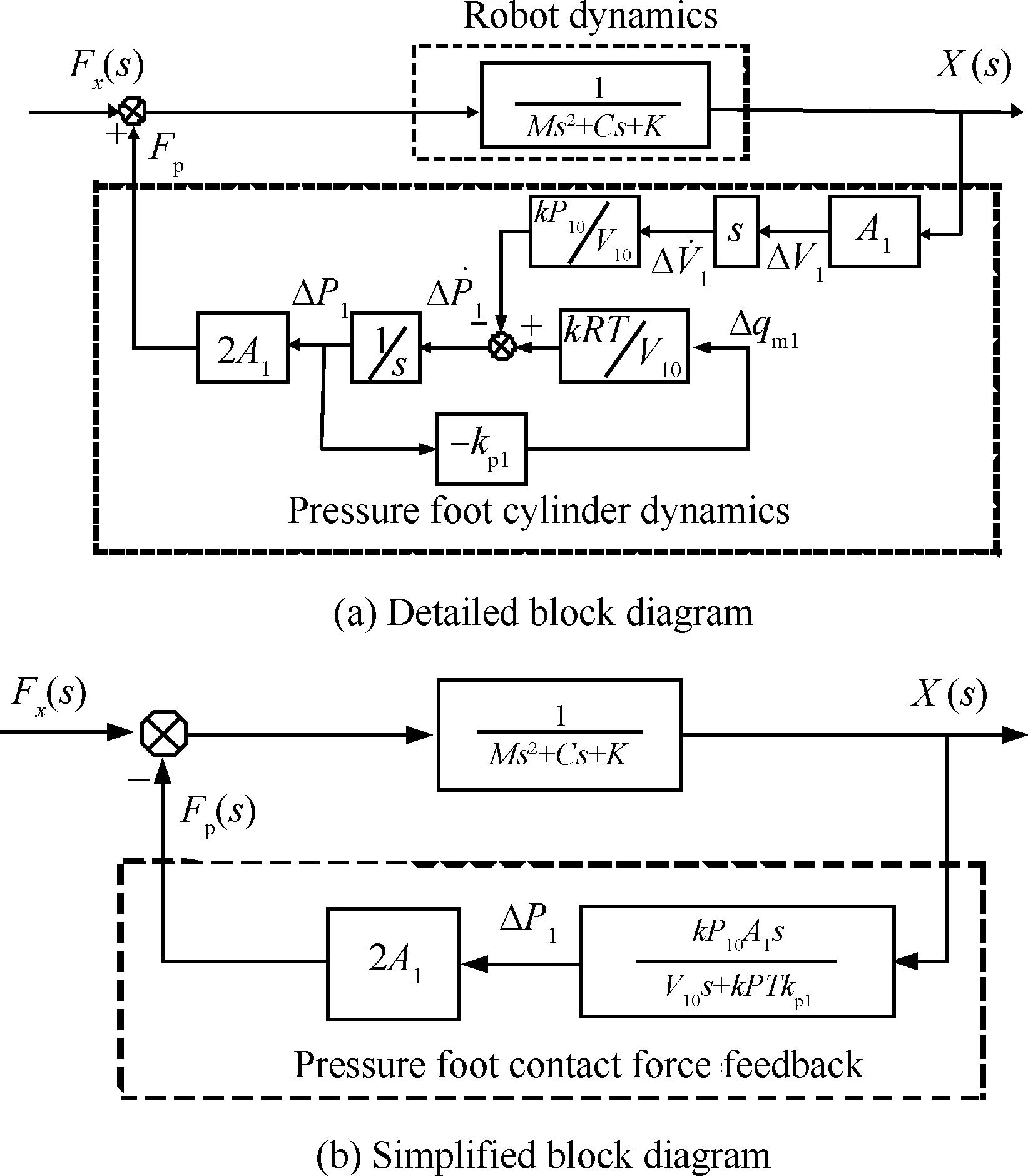
镗孔过程中,机器人加工系统仅受镗削力F作用,在初始平衡点处作微幅振动,如图4所示,气缸内气压变化连续且变化幅度较小,压脚杆在气缸左腔高气压的作用下始终紧贴在工件表面。同时考虑工件为刚体。此时气动压脚的作用相当于一个“气动弹簧”,连接机器人末端和工件,该“气动弹簧”的引入改变了原有的机器人镗孔系统的动力学特性。
对施加压脚后的机器人镗孔系统进行受力分析,如图5所示,系统在进给方向x上的动力学方程为
(8)
式中:(P1,A1)、(P2,A2)分别为气缸左(Ⅰ腔)、右(Ⅱ腔)两腔工作气体压力和活塞接触面积参数。
压脚工作时,气缸右腔直通大气,可认为气压在工作过程中近似不变,为大气压力Patm,则右腔压力P2=Patm= 0.1 MPa。假设左腔为理想气体经历一个等熵绝热过程,同时不考虑气体的泄漏,则左腔气体质量流量方程为[18]
(9)
式中:qm1为左腔气体的质量流量;k为气体热力学常数;R为气体常数;T为供气气源温度;V1、V2分别为气缸左、右腔的有效容积。
对式(9)在平衡点处(压脚伸出紧贴工件时活塞的初始位置)进行拉普拉斯变换,得
(10)
式中:V10和P10分别代表平衡点处气缸左腔的有效容积和压力。V10=LsA1,Ls为施加压脚后,压脚杆伸出距离。
压脚工作时,左腔气体的流量变化靠节流阀的开口面积Sc1控制,根据气体经过小孔的流量方程,得
(11)
其中
f(Pd/Pu)=
(12)
式中:Cd为节流阀节流口流量系数;ρu为节流口上部气体密度;Pu、Pd分别为节流口上、下游气体压力。
气体经过小孔的压力-流量特性为非线性过程,对式(11)在平衡工作点处利用泰勒公式展开作小偏差线性化,同时进行拉普拉斯变换,得
qm1(s)=kf1Sc1(s)-kp1P1(s)
(13)
式中:压脚气缸左腔空气的质量-流量系数kf1= ∂qm1/∂Sc1;压力-流量系数kp1=-∂qm1/∂P1。
对于机器人镗孔系统,镗孔前先通过比例减压阀设置压脚气动系统的工作压力,通常为相对大气压力0.3MPa,并且在镗孔过程中不再对压力值进行调整,故比例阀的开口恒定,则有kf1=∂qm1/∂Sc1=0。
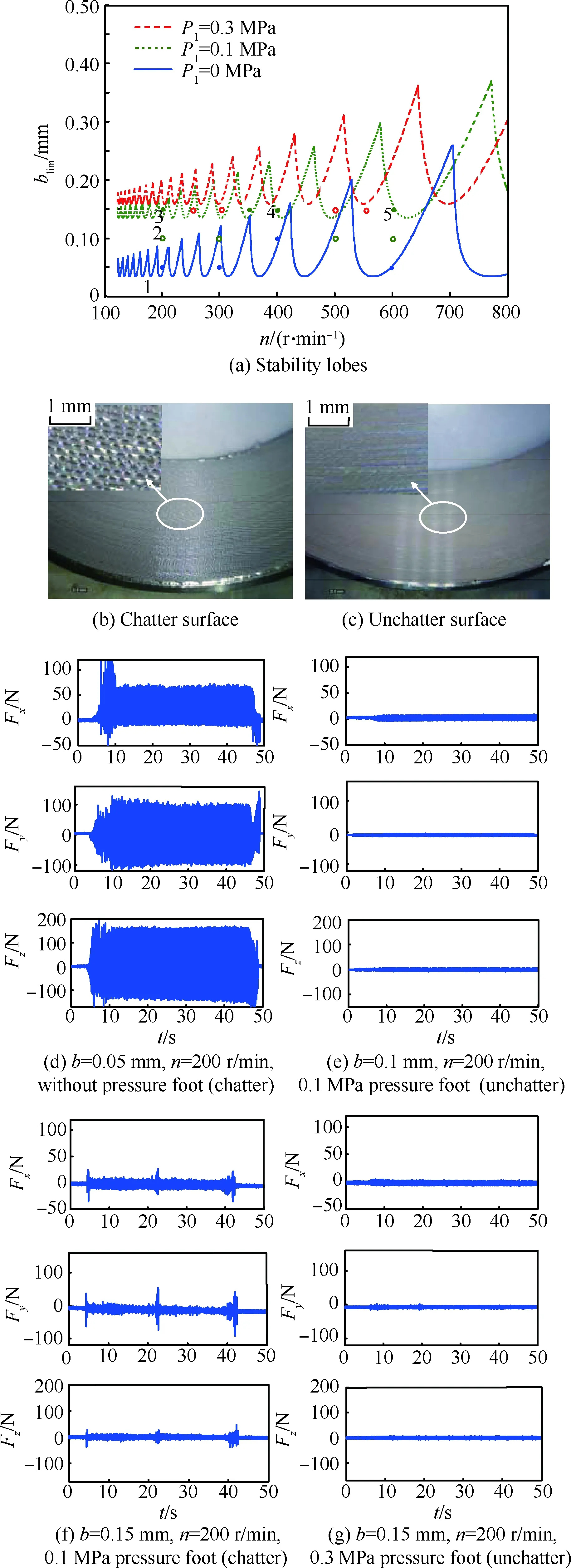
对于压力-流量系数kp1,由于工作时系统仅作微幅振动,故气动压脚回路内满足关系0.528 (14) 式中:PS1为左腔对应节流口上游气体压力,即气压源供气压力;P10为左腔对应节流口下游气体压力,即平衡点处压脚气缸左腔压力。由式(10)和式(13),进一步得 (15) 对式(8)在平衡点处进行拉普拉斯变换,可得 MX(s)s2+CX(s)s+KX(s)-2P1(s)A1=Fx(s) (16) 将式(15)代入式(16)中,可以得到系统动力学方程的拉氏变换式 MV10X(s)s3+(CV10+MkRTkp1)X(s)s2+ KkRTkp1X(s)=V10Fx(s)s+kRTkp1Fx(s) (17) 进一步得到系统进给方向上的传递函数为 (18) 图6 压脚作用下机器人镗孔系统方框图 Fig. 6 Block diagram of robot boring system with pressure foot 图7 未加压脚时机器人镗孔系统方框图 Fig. 7 Block diagram of robot boring system without pressure foot 若不施加压脚,压脚杆未伸出压实工件,此时机器人仅以一悬臂梁结构进行加工。令式(8)中P1=P2=0,去除压脚气缸对系统的影响,则无压脚作用情况下系统的传递函数框图如图7所示。此时,系统在进给方向上的传递函数为 (19) 比较图6和图7,当施加压脚作用后,机器人镗孔系统在加工过程中会引起压脚气缸内压力波动,形成一个压脚力负反馈作用在系统上,从而改变了开链串联机器人结构原有的动力学特性。为了进一步分析施加压脚后,机器人镗孔系统对镗孔加工稳定性的影响,需建立镗削力模型。 以主轴转速为横坐标,径向切深为纵坐标绘制的镗削稳定性叶瓣图是预测加工系统稳定性的有效工具[19]。根据之前建立的机器人镗孔系统的传递函数,结合镗削条件,通过建立稳定性数学模型,计算出径向切深和主轴转速的临界值,能够快速地绘制出机器人镗孔系统加工过程稳定性叶瓣图。 3.1 动态镗削力建模 图8 镗孔切削示意图 Fig. 8 Boring cutting process diagram 在机器人镗孔过程中,沿主轴进给方向的镗削厚度h可分为两部分:静态和动态镗削厚度。从图8(a)和图8(b)中可以看出,b为实际镗削深度,切削方向z向的运动不影响进给方向上镗削厚度的变化,因此镗削厚度的建模可以简化为二维加工平面内的问题。机器人镗孔加工实际上为斜角切削,进行镗削过程分析时参考斜角切削模型。刀尖上的3个刀具角度为: 主偏角κr,前角γ0,刃倾角λs。总的镗削厚度为 sin(90°-κr) (20) 式中:l为主轴每转一圈进给方向上的进给量;(x(t),y(t))为当前时刻刀尖点在工具坐标系下加工平面内的实际动态坐标;(x(t-T1),y(t-T1))为前一周期刀尖点实际动态坐标,T1为时延,表示主轴每转一圈所花的时间。单位进给量lcos(90°-κr)为总镗削厚度中的静态部分。 由于静态镗削厚度不影响振动的产生,故进行镗削过程稳定性分析时可将其忽略。因此,机器人镗孔过程中,动态切削厚度的变化为 Δh(t)=Δxcos(90°-κr)+Δysin(90°-κr) (21) (22) 尽管机器人镗孔镗削加工的动力学问题可以简化为二维平面内的问题,但实际镗削加工仍然是在三维空间内进行的。由于镗刀刀片上各种刀具角度的存在,进行镗削力分析时仍然要在三维空间内进行。 图9 切削刀片受力分析 Fig. 9 Force analysis of cutting tool 如图9所示,机器人镗孔时,作用在镗孔刀片切削刃上的总镗削力可以分解为3个部分:平行于切削速度方向的切向切削力Ft,垂直于由切削速度方向和切削刃所构成的平面的进给切削力Ff,垂直于Ft和Ff所构成平面的径向切削力Fr。 根据图8(a)中的几何关系与式(21),加工平面内的动态切削力为 (23) 式中:Kf和Kr为两个相关的切削力系数。通过坐标系旋转变换,将进给切削力Ff和径向切削力Fr变换至刀具坐标系下 (24) 将式(23)代入式(24)中,可得 F=bBΔd (25) (26) 3.2 镗削稳定性分析 机器人镗孔系统在加工过程中,刀尖点受到切削力干扰而产生振动,在颤振频率点ωc处的振动位移为 d(jωc)=G(jωc)F (27) 式中:G(jω)为系统的传递函数矩阵,其定义为 (28) 其中:Gxx和Gyy为系统分别在x方向和y方向的直接传递函数;Gxy和Gyx为系统的交叉传递函数。 在时刻t的振动d和前一镗削周期t-T1的振动d0的关系为 d0(jωc)=e-jωcT1d(jωc) (29) 将式(27)代入式(25)中,并利用式(29)的关系,此时动态切削力可以表示为 F=b(1-e-jωcT1)BG(jωc)F (30) 式(30)为关于动态切削力F的方程,该方程有非奇异解的条件为 det(I+ΛG0(jωc))=0 (31) 式中:I为单位矩阵;G0(jωc)=BG(jωc)为有向传递函数矩阵,该方程的特征值Λ可表示为 Λ=b(e-jωcT1-1) (32) 忽略系统传递函数矩阵中的交叉传递函数Gxy和Gyx,式(31)的解为 Λ=-sinκr/[Gxx(-Kfsin2κr+Krcosκrsinκr)+ Gyy(-Kfcos2κr-Krcosκrsinκr)] (33) 传递函数为复数,其特征值包含实部和虚部,将Λ=ΛR+jΛI及欧拉公式e-jωcT1=cosωcT1-j sinωcT1代入式(32),可以得到在颤振频率ωc处的临界镗削深度为 (34) 由于实际临界镗削深度blim应为正实数,故式(34)的虚部应为零,可得: (35) 于是得到临界镗削深度的最终表达式为 (36) 利用式(35)可以得到颤振频率和镗削周期的关系: (37) 式中:k′为叶瓣数。镗孔时主轴转速可通过求镗削周期得到: (38) 可得主轴转速: (39) 实验系统由ABBIRB6600型工业机器人、末端执行器、加工衬套孔、KISTLER9257B测力仪以及控制系统构成。由于环境的限制,对于实际现场的飞机主起交点框,通过立柱框架结构来模拟,对于主起落架交点框上的双叉耳孔,取两段带衬套的圆孔并排固定在立柱框架结构上进行模拟,实验平台如图10所示。 图10 机器人镗孔实验系统 Fig. 10 Robot boring experiment system 实验加工对象——双叉耳孔衬套(内径42mm)为一种马氏体沉淀硬化不锈钢PH13-8Mo[20]。该钢强度高、断裂韧性好,能够满足飞机起落架大冲击、重载荷的需要,在航空结构材料中应用广泛。由于该材料良好的综合性能,对于加工刀具也有很高的要求。本系统采用日本大昭和精机株式会社BIG-KAISER镗刀系列产品,具体型号如下:刀柄型号为BT30-CK3-120;镗杆型号为CK43-45;精镗头型号为EWN32-60CKB3;镗刀片型号为AC520U。三棱型刀片通过螺栓连接夹紧在精镗头上,其上的刀具角度如下:主偏角κr=80°,前角γ0=8°,刃倾角λs=11°。切削力系数取Kf=850N/mm2,Kr=130N/mm2,由实验现场环境确定气体状态参数,进一步查阅气动元件产品说明书,综合得到气动压脚系统的各参数如表3所示。 表3 气动压脚系统参数 在完成机器人镗孔系统动力学建模并求解传递函数的基础上,绘制稳定性叶瓣图,进而预测机器人镗孔系统的加工稳定性,并研究有无压脚作用和不同压脚气缸压力情况下对机器人镗孔加工系统加工稳定性的影响,具体步骤如下: 步骤 1 在系统固有频率附近选取扫描颤振频率ωc,根据式(36)计算不同颤振频率ωc下,机器人镗孔系统的稳定镗削深度blim,筛选出满足特征值Λ、具有负实部的颤振频率点ωc。 步骤 2 针对不同的叶瓣数k′,通过式(39)计算得到相应的主轴转速n. 步骤 3 以主轴转速n为横坐标,极限切深blim为纵坐标,得到机器人镗孔系统镗削稳定性叶瓣图。 根据以上计算流程,在式(33)中分别代入未施加压脚情况下系统传递函数式(19)和压脚作用下系统传递函数式(18),并改变压脚压力参数。在同一个坐标系中分别绘制出压脚压力P1=0.1、0.3 、0 MPa(未施加压脚)3种情况下系统的稳定性叶瓣图。 图11为机器人镗孔加工稳定性叶瓣图和分析结果。从图11(a)可以看出,在叶瓣以上将发生颤振,叶瓣底部以下在加工过程中为绝对稳定区域。未施加压脚时,机器人镗孔系统的绝对稳定切深在0.05 mm以下。图11(a)中1点处为未施加压脚情况下采用0.05 mm切深、200 r/min转速进行机器人镗孔加工实验,图11(b)和图11(d)分别为1点处的衬套孔内表面质量和切削力,可以观察到系统发生严重的颤振。当施加0.1 MPa压脚压力后,叶瓣曲线向上向右移动,绝对稳定切深增大,拓展了机器人镗孔系统的可加工稳定镗削参数范围。图11(a)中2点处为施加0.1 MPa压脚后采用0.1 mm切深、200 r/min转速进行机器人镗孔加工实验,图11(c)和图11(e)分别为该点处的衬套孔内表面质量和切削力,没有发生颤振。但在此参数上将切深进一步提高至0.15 mm,如点3所示,实验系统再次发生颤振,此时的切削力如图11(f)所示,相比于未加压脚系统发生颤振时,如图11(d),颤振切削力明显减小,可见压脚对于机器人镗孔系统颤振幅值的抑制效果明显。此时,将压脚压力提高至0.3 MPa,颤振消失,切削力如图11(g)所示,镗削过程平稳。点4、5处同样验证了这一变化。实验结果与利用再生颤振原理绘制出的稳定性叶瓣图预测得到的稳定域基本符合,可认为在此种加工环境下机器人发生了再生颤振,再生颤振是机器人加工中可能发生的一种颤振类型。 图11 压脚作用下机器人镗孔系统稳定性分析 Fig. 11 Stability analysis of robot boring system under influences of pressure foot 机器人镗孔系统的稳定镗削深度随着气动压脚的引入和压脚压力的增大而进一步拓展,系统的加工稳定性增强。但在实际机器人镗孔应用中,考虑到过大的压脚压力使机器人产生过大的静态变形对机器人镗孔精度的影响,实际加工过程中一般设定压脚压力为0.3 MPa,可满足加工稳定要求。 1) 构建了机器人镗孔系统,解决大型飞机主起落架交点孔的镗孔精加工问题,采用压脚装置解决机器人镗孔颤振问题,拓展了机器人在这一领域内的应用。 2) 建立了机器人镗孔系统加工稳定性理论分析模型,包括机器人系统模型、气动压脚模型以及镗削加工过程模型,绘制了加工稳定性叶瓣图,研究了压脚作用对稳定性叶瓣图的影响。 3) 根据实验数据和理论模型,研究了压脚作用对机器人镗孔系统加工稳定性的影响,得到了压脚的引入和合理选择压脚压力可以拓展稳定加工工艺参数范围,增大极限切削深度,提高系统加工稳定性的结论。 [1] 许国康. 大型飞机自动化装配技术[J]. 航空学报, 2008, 29(3): 734-740. XU G K. Automatic assembly technology for large aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(3): 734-740(in Chinese). [2] 沈建新, 田威. 基于工业机器人的飞机柔性装配技术[J]. 南京航空航天大学学报, 2014, 46(2): 181-189. SHEN J X, TIAN W. Aircraft flexible assembly technology based on industrial robots[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2014, 46(2):181-189 (in Chinese). [3] ZHANG H, WANG J J, ZHANG G, et al. Machining with flexible manipulator: Toward improving robotic machining performance[C]//International Conference on Advanced Intelligent Mechatronics. Piscataway, NJ: IEEE Press, 2005: 1127-1132. [4] QUINTANA G, CIURANA J. Chatter in machining processes: A review[J]. International Journal of Machine Tools & Manufacture, 2011, 51(5): 363-376. [5] ÖZER A, SEMERCIGIL S. Tool chatter in turning with a two-link robotic arm[J]. Journal of Sound and Vibration, 2013, 332(6): 1405-1417. [6] PAN Z X, ZHANG H, ZHU Z Q, et al. Chatter analysis of robotic machining process[J]. Journal of Materials Processing Technology, 2006, 173(3): 301-309. [7] DEVLIEG R, SITTON K, FEIKERT E, et al. ONCE(one-sided cell end effector) robotic drilling system[C]//SAE 2002 Automated Fastening Conference and Exposition. Warrendale: SAE, 2002: 2002-01-2626. [8] 邓锋. 采用标准关节机器人系统对飞机货舱门结构的自动钻铆[J]. 航空制造技术, 2010(9): 32-35. DENG F. Automated fastening of aircraft cargo door structures with a standard articulating robot system[J]. Aeronautical Manufacturing Technology, 2010(9): 32-35 (in Chinese). [9] 费少华, 方强, 孟祥磊, 等. 基于压脚位移补偿的机器人制孔锪窝深度控制[J]. 浙江大学学报:工学版, 2012, 46(7): 1157-1161. FEI S H, FANG Q, MENG X L, et al. Countersink depth control of robot drilling based on pressure foot displacement compensation[J]. Journal of Zhejiang University:Engineering Science, 2012, 46(7): 1157-1161 (in Chinese). [10] OLSSON T, HAAGE M, KIHLMAN H, et al. Cost-efficient drilling using industrial robots with high-bandwidth force feedback[J]. Robotics and Computer-Integrated Manufacturing, 2010(26): 24-38. [11] 王珉, 薛少丁. 飞机大部件对接自动化制孔单向压紧力分析[J]. 南京航空航天大学学报, 2012, 44(4): 554-558. WANG M, XUE S D. One-side pressure-force analysis of automatic drilling of aircraft fuselage section-joint assembly[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2012, 44(4): 554-558 (in Chinese). [12] 邱宝贵, 蒋君侠, 毕运波, 等. 大型飞机机身调姿与对接试验系统[J]. 航空学报, 2011, 32(5): 908-919. QIU B G, JIANG J X, BI Y B, et al. Posture alignment and joining test system for large aircraft fuselages[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(5): 908-919 (in Chinese). [13] 郭志敏, 蒋君侠, 柯映林. 基于POGO柱三点支撑的飞机大部件调姿方法[J]. 航空学报, 2009, 30(7): 1319-1324. GUO Z M, JIANG J X, KE Y L. Posture alignment for large aircraft parts based on three POGO sticks distributed support[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(7): 1319-1324 (in Chinese). [14] ABELE E, WEIGOLD M, ROTHENBUCHER S. Modeling and identification of an industrial robot for machining applications[J]. CIRP Annals-Manufacturing Technology, 2007, 56(1): 387-390. [15] ANGELES J. On the nature of the Cartesian stiffness matrix[J]. Ingeniería Mecánica, 2010, 3(5): 163-170. [16] 曲巍崴, 侯鹏辉, 杨根军, 等. 机器人加工系统刚度性能优化研究[J]. 航空学报, 2013, 34(12): 2823-2832. QU W W, HOU P H, YANG G J, et al. Research on the stiffness performance for robot machining systems[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(12): 2823-2832 (in Chinese). [17] BISU C, CHERIF M, GÉRARD A, et al. Dynamic behavior analysis for a six axis industrial machining robot[J]. Advanced Materials Research, 2012, 423(1): 65-76. [18] QIU Z, SHI M, WANG B, et al. Genetic algorithm based active vibration control for a moving flexible smart beam driven by a pneumatic rod cylinder[J]. Journal of Sound and Vibration, 2012, 331(10): 2233-2256. [19] 孔天荣, 梅德庆, 陈子辰. 磁流变智能镗杆的切削颤振抑制机理研究[J]. 浙江大学学报: 工学版, 2008, 42(6): 1005-1009. KONG T R, MEI D Q, CHEN Z C. Research on mechanism of cutting chatter suppression based on magnetorheological intelligent boring bar[J]. Journal of Zhejiang University: Engineering Science, 2008, 42(6): 1005-1009 (in Chinese). [20] JONG M, SCHMALZ F, RENSMAN J W, et al. Post-irradiation characterization of PH13-8Mo martensitic stainless steel[J]. Journal of Nuclear Materials, 2011, 417(1): 145-148. 方强 男, 博士, 教授。主要研究方向: 飞机数字化装配、机器人制孔。 Tel: 0571-87953929 E-mail: fangqiang@zju.edu.cn 李超 男, 硕士研究生。主要研究方向: 机器人制孔。 E-mail: mcsuperli@126.com 费少华 男, 硕士, 助理研究员。主要研究方向: 伺服控制。 E-mail: f307110@163.com 孟涛 男, 本科, 工程师。主要研究方向: 飞机部件装配。 E-mail:mengtao51378@qq.com Received: 2015-01-06; Revised: 2015-02-06; Accepted: 2015-02-26; Published online: 2015-03-25 12:51 URL: www.cnki.net/kcms/detail/11.1929.V.20150325.1251.004.html Foundation item: Zhejiang Provincial Natural Science Foundation(LY13E050009) *Corresponding author. Tel.: 0571-87953929 E-mail: fangqiang@zju.edu.cn Stability analysis of robot boring system FANG Qiang1,*, LI Chao1, FEI Shaohua1, MENG Tao2 1.CollegeofMechanicalEngineering,ZhejiangUniversity,Hangzhou310027,China2.MilitaryAgent’sRoomofXi’anAircraftIndustry(Group)CompanyLTD,People’sLiberationArmy,Xi’an710089,China In order to perform the finish boring procedure of the aircraft landing gear’s junction hole in the aircraft assembly field, a six axis industrial robot with a special designed end-effector system is proposed. The structure of pressure foot is a key technology to avoid chatter in this robot boring system. Through establishing an analytical model for stability limit prediction considering dynamical characteristics with and without pressure foot structure of the robot boring system, the chatter stability lobes is achieved and studied to reveal the mechanism of the chatter depressing of the pressure foot. In addition, experiments are conducted to verify the rationality of the theoretical modeling under different pressure foot parameter condition. The analytical model and experiments show that the stability of the robot boring process can be enhanced by applying pressure foot system and choosing a rational pressure value. Stable machining area is expanded and chatter is avoided. pressure foot; industrial robot; boring; chatter; stability lobes 2015-01-06; 退修日期: 2015-02-06; 录用日期: 2015-02-26; < class="emphasis_bold">网络出版时间: 时间:2015-03-25 12:51 www.cnki.net/kcms/detail/11.1929.V.20150325.1251.004.html 浙江省自然科学基金 (LY13E050009) .Tel.: 0571-87953929 E-mail: fangqiang@zju.edu.cn 方强, 李超, 费少华, 等. 机器人镗孔加工系统稳定性分析[J]. 航空学报, 2016, 37(2): 727-737. FANG Q, LI C, FEI S H, et al. Stability analysis of robot boring system [J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(2): 727-737. http://hkxb.buaa.edu.cn hkxb@buaa.edu.cn 10.7527/S1000-6893.2015.0064 V19; TP242.2 : A : 1000-6893(2015)02-0727-11 *

3 镗孔加工稳定性分析



4 加工过程稳定域的仿真与实验分析


5 结 论
