由裂纹嘴位移确定双悬臂梁试样应力强度因子的权函数解法

童第华， 吴学仁， 刘建中 中航工业北京航空材料研究院， 北京 100095

由裂纹嘴位移确定双悬臂梁试样应力强度因子的权函数解法

童第华， 吴学仁*， 刘建中 中航工业北京航空材料研究院， 北京 100095

双悬臂梁(DCB)试样在材料的损伤容限性能评价，特别是应力腐蚀开裂门槛值(KISCC)测定中有重要应用。由于该试样几何的特殊性，一般采用与试样端部(裂纹嘴)有一定距离的特定位置裂纹面位移加载方式，然而该加载点的位移测量不但费时而且精度低,位移测量最方便和准确的位置是在DCB试样的裂纹嘴。通过对一种参考载荷条件的有限元计算，应用边缘裂纹的经典权函数解法，推导出DCB试样的权函数解析解，并与复变函数泰勒级数展开的权函数解法作了比较验证。在此基础上根据特定加载点的位移反算出相应位置均布应力加载下的应力强度因子，进而建立DCB试样在特定位置的裂纹面位移加载条件下的应力强度因子与裂纹嘴位移之间的关系式，为采用这种试样的材料损伤容限性能评价，特别是KISCC的高精度自动化测定奠定了基础。

双悬臂梁试样； 权函数； 位移加载条件； 应力强度因子； 裂纹嘴位移

双悬臂梁(DCB)试样(图1)被广泛用于材料的损伤容限性能评价，特别是应力腐蚀开裂门槛值(KISCC)的测定[1-4]，因此需要这种试样在不同加载情况下的高精度应力强度因子解。但文献中对于DCB试样的断裂力学分析，尤其是位移加载情况下的应力强度因子计算，鲜有涉及。

国家标准GB/T 15970.6—2007[4]中给出的DCB试样在位移加载情况下的应力强度因子表达式是根据梁的弹性柔度理论得到的，它适用于中心位于x=d点的螺栓对裂纹面进行位移加载的情况u(a/W,x/W=d/W)，见图1，其中：W为试样的特征尺寸，本文中取为试样宽度；a为裂纹长度。相比于位于试样端部的裂纹嘴处的位移u(a/W,x/W=0)，该加载点位移的测定不但很不方便，而且准确性差，更难以实现自动化测量。而裂纹嘴处的位移却能够通过位移规很准确地获得。本文旨在根据裂纹嘴处的位移u(a/W,x/W=0)确定DCB试样在裂纹面位移加载条件下的高精度应力强度因子，从而为采用这种试样的材料损伤容限性能评价，特别是KISCC的高精度自动化测定提供理论依据。

图1 双悬臂梁(DCB)试样 (a=l+d)

Fig.1 Double cantilever beam (DCB) specimen (a=l+d)

1 二维裂纹问题的权函数法

在众多的应力强度因子求解方法中，权函数法[5-9]以其高度的普适性、出色的求解效率、可靠的精度和便于应用的特点，在裂纹问题的分析中得到了日益广泛的应用。权函数一经确定，就可用来不受限制地求解该裂纹体在任意受载条件下的应力强度因子。本文根据Wu(吴学仁)和Carlsson权函数方法[7-8]确定DCB试样的权函数解析表达式，进而利用螺栓中心线处的裂纹面位移或裂纹嘴处的位移求解裂纹面位移加载情况下的应力强度因子。

断裂力学的权函数理论最早是由Bueckner[5]和Rice[6]提出的，其基本思想是将影响裂纹尖端应力强度因子的2个变量——载荷和裂纹体几何进行分离，得到独立于载荷情况(仅包含裂纹体几何信息(包括载荷-位移边界条件))的权函数。Wu和Carlsson系统地给出了各类二维裂纹问题权函数的解析推导方法[7-8]。

对于应力强度因子，有

(1a)

(1b)

式中：σ(x/W)/σ为假想裂纹处的无量纲应力分布；m(a/W,x/W)为所考虑裂纹体的权函数。

裂纹面位移与权函数存在如式(2)所示的关系。

(2)

式中:E′=E(平面应力),E′=E/(1-ν2)(平面应变)，E为弹性模量，ν为泊松比；f(s/W)见式(1b)，其中s为积分变量。

DCB试样属于边缘裂纹，根据文献[7-8]，这类裂纹的权函数通式为

(3)

式中：

(4)

(5a)

(5b)

(6a)

(6b)

式中：αi和γi为多项式系数。

式(3)～式(6)表明，为了得到权函数，需要先有一种参考载荷作用下的应力强度因子fr和裂纹嘴位移ur的表达式(式(6))。根据文献[7-8]对边缘裂纹权函数的推导方法，将已知的fr和ur代入式(4)和式(5)，就能确定φ和F1～F4，进而确定DCB试样的权函数系数βi(a/W)。将βi(a/W)代入式(3)，便得到DCB试样的权函数m(a/W,x/W)。本文采用ABAQUS有限元数值程序[10]求解该试样在一种参考载荷作用下的高精度应力强度因子解fr和裂纹嘴张开位移ur，作为拟合式(6)的基础数据，详见第2节。

2 DCB试样的宽范围权函数解

针对双悬臂梁试样，利用有限元程序ABAQUS建立不同a/W的有限元模型(试样宽度W=100 mm，试样高度h=10 mm)，如图2所示。裂纹尖端局部网格划分如图3所示，裂纹尖端采用退化的1/4节点奇异元，其他单元采用二次八节点等参元。加载形式为远端均匀应力。

ABAQUS有限元计算可以直接给出应力强度因子和裂纹嘴张开位移。由于权函数分析通常采用无量纲的应力强度因子和裂纹嘴张开位移，在此将ABAQUS有限元结果转化为无量纲形式，如表1所示。

图2 DCB试样的有限元模型(由于对称性，取一半)

Fig.2 Finite element model of DCB specimen (Because of symmetry, only half of DCB specimen was modelled)

图3 裂纹尖端局部网格划分

Fig.3 Finite element mesh of crack tip region

表1 不同裂纹长度情况下的无量纲应力强度因子和裂纹嘴位移(DCB试样受远端均匀应力作用)

Table 1 Normalized stress intensity factor and crack mouth displacement (DCB specimen subjected to remote uniform tension)

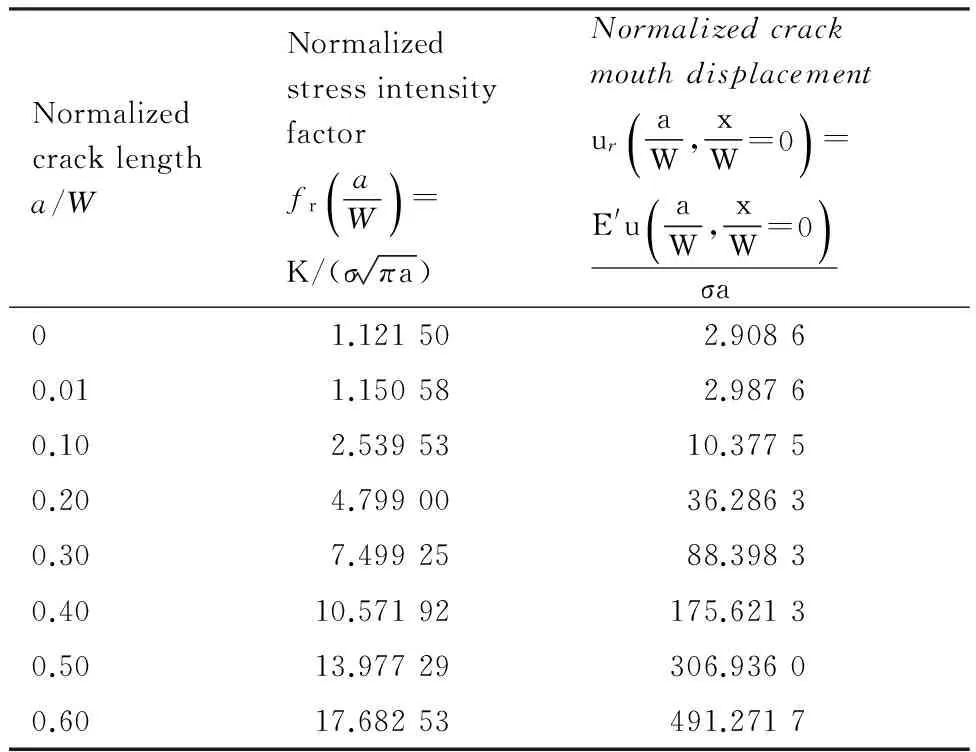
Normalizedcracklengtha/WNormalizedstressintensityfactorfraW()=K/(σπa)NormalizedcrackmouthdisplacementuraW,xW=0()=E'uaW,xW=0()σa01.121502.90860.011.150582.98760.102.5395310.37750.204.7990036.28630.307.4992588.39830.4010.57192175.62130.5013.97729306.93600.6017.68253491.2717

结合半无限大板边缘裂纹的理论极限值fr=1.121 5和ur=2.908 6,通过拟合表1中DCB试样的无量纲应力强度因子fr和无量纲裂纹嘴位移ur结果，即可得到多项式(6a)和式(6b)中的相应系数αi和γi，结果如下所示：当a/W≤0.6时，αi(i=0～6)=1.102 6, 4.454 1, 103.03, -531.32, 1 271.0, -1 584.3, 789.59；当a/W≤0.6时，γi(i=0～6)=2.900 3, -2.383 5, 624.56, -516.87, 290.29, -1 914.5, 1 611.5。

将以上系数代入式(6a)和式(6b)，fr和ur拟合得到的曲线与有限元结果的最大差别为1.7%和0.29%，如图4所示。将式(6a)和式(6b)代入式(4)和式(5)，即可得到式(3)中DCB试样的权函数系数βi(a/W)，如表2所示。表2中，a/W=0的权函数系数βi值引自文献[7]中半无限大板边缘裂纹的理论极限值。

图4 DCB试样受远端均匀应力作用下的无量纲应力强度因子和无量纲裂纹嘴位移拟合曲线

Fig.4 Fitting curves of normalized stress intensity factor and crack mouth displacement of DCB specimen subjected to remote uniform tension

为了验证本文求得的DCB试样的解析权函数的精度，把所得结果与文献中用其他方法确定的权函数进行了比较。Jing(景致)和Wu(吴学仁)利用复变函数泰勒级数展开方法(WCTSE)确定了DCB试样的权函数[11]。Fett和Munz[9]也给出了DCB试样的权函数表达式，如式(7)所示。

表2 通过Wu和Carlsson权函数方法[7-8]确定的DCB试样权函数系数值

Table 2 Weight function coefficients for DCB specimen based on Wu and Carlsson weight function method[7-8]

a/Wβ1(a/W)β2(a/W)β3(a/W)β4(a/W)β5(a/W)02.00.97881.1101-0.3194-0.10170.012.01.74140.2945-0.1467-0.08400.102.08.86821.58633.6753-1.62910.202.018.114014.5490-1.7245-0.16190.302.028.829125.98790.0722-1.60620.402.039.979043.9685-3.4196-1.33230.502.052.360361.5146-3.0837-2.62650.602.064.788780.51691.0404-5.6676

(7)

确定了DCB试样的权函数后，对于载荷边界条件下的应力强度因子的计算，可以通过式(1)一个简单的积分得到。对于位移边界条件下的应力强度因子计算，则可以通过已知的裂纹面位移，对式(2)进行逆运算得到，详见第3节。

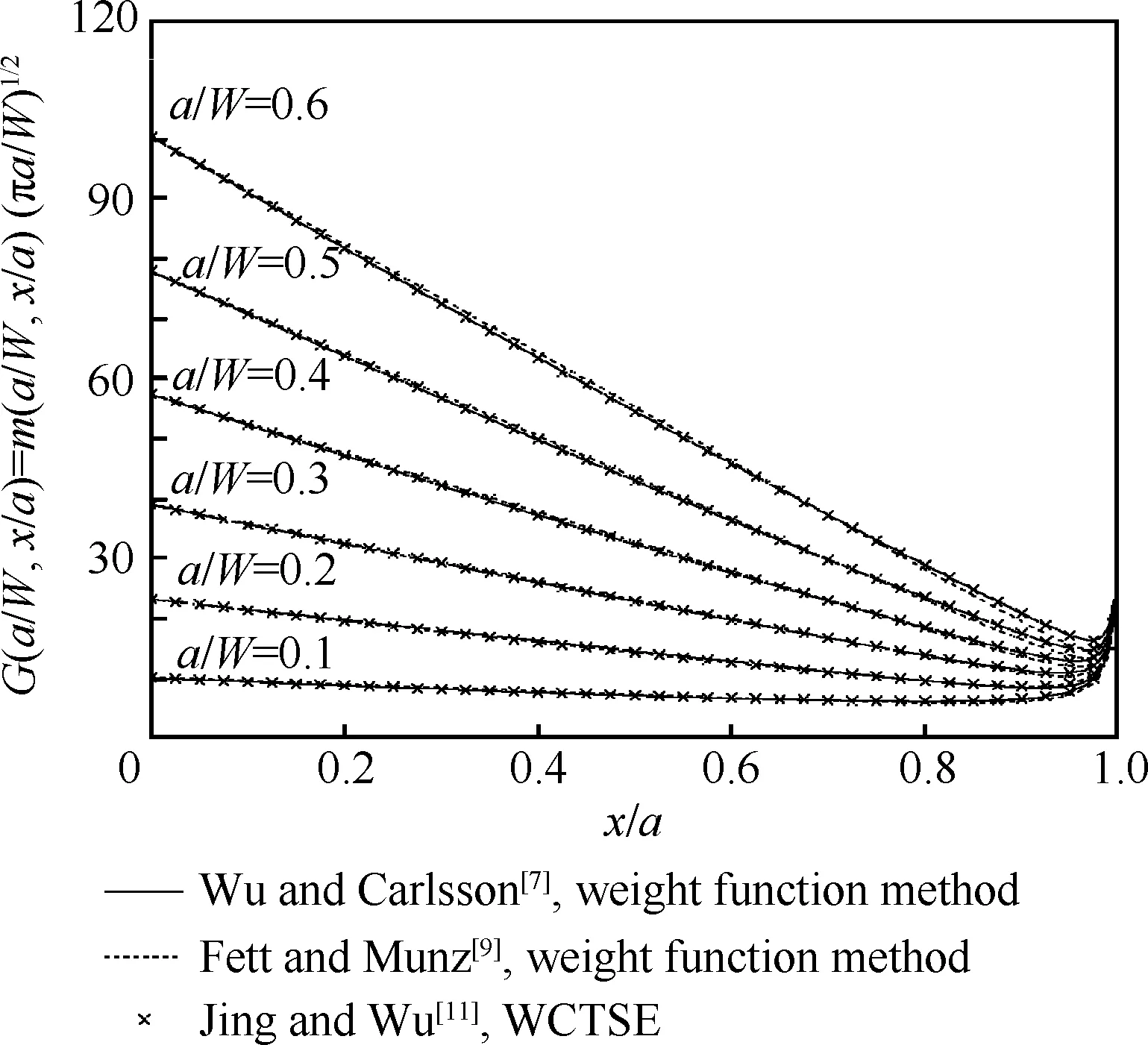
图5 DCB试样的3种格林函数(权函数)的比较

(a/W=0.1～0.6)

Fig.5 Comparison of three Green’s functions (weight function) for DCB specimen (a/W=0.1-0.6)

3 DCB试样在点位移加载下的应力强度因子求解

DCB试样通过螺栓实现位移加载(见图1)，这种加载形式相当于裂纹面受区段均布应力σ作用，其作用宽度为螺栓的直径，应力σ的具体数值则只能通过位移间接确定。

裂纹面区段均匀应力作用下的应力强度因子可以写为[7-8]

(8a)

(8b)

式中：d1和d2见图1。

在未知区段均布应力值σ的情况下，无法通过式(8)确定应力强度因子。Wu和Carlsson[7-8]给出了裂纹面区段均布应力作用下的裂纹面位移表达式为

(9a)

(9b)

将第2节中通过Wu和Carlsson权函数法确定的权函数系数βi表达式和裂纹面的位移代入到式(9)中，即可确定裂纹面区段均布应力σ的值。

图6给出了根据裂纹面位移和相应裂纹几何的权函数确定区段均布应力值和应力强度因子的流程图。该方法是一种普适方法，不仅适用于DCB试样，也适用于其他各种裂纹几何。

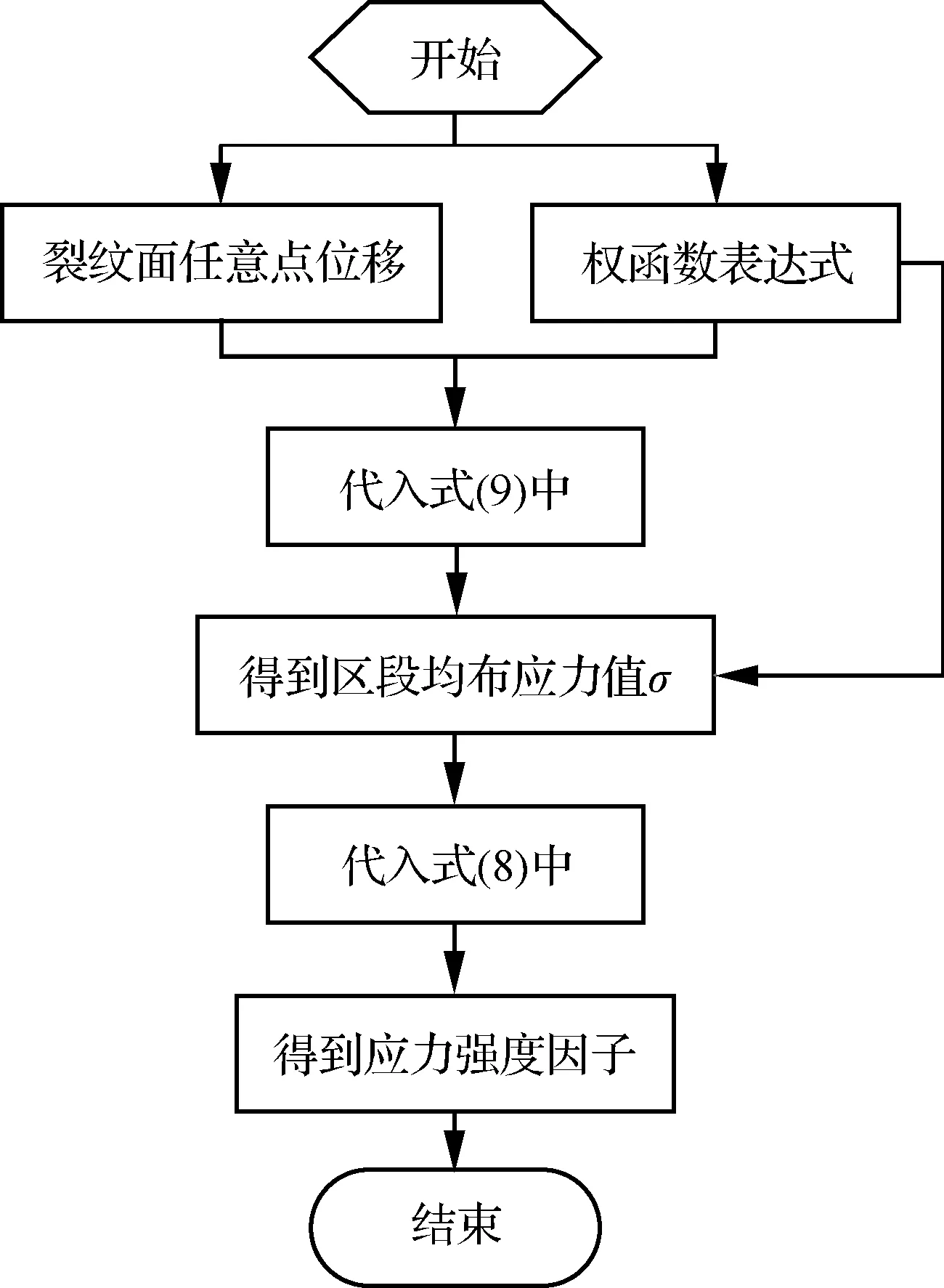
图6 利用裂纹面位移确定区段均布应力值σ和应力强度因子的流程图

Fig.6 Flowchart of determination of segment uniform stress σ and stress intensity factor using crack surface displacements

GB/T 15970.6—2007[4]中给出了DCB试样在螺栓加载情况下根据加载点位移u求解应力强度因子的表达式为

(10)

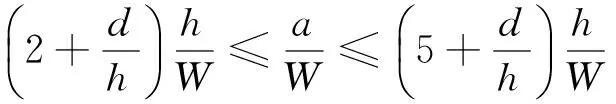
为了将权函数计算结果和式(10)进行对比，这里以d/W处的位移作为已知条件。对于图1所示的DCB试样，取W=100 mm，h=10 mm，d=10 mm，螺栓直径为7.5 mm，a/W=0.3, 0.4, 0.5, 0.6(与式(10)的适用范围2≤l/h≤5对应)。结合第2节中通过Wu和Carlsson权函数法得到的DCB试样权函数和式(9)，得到了区段均布应力值与d/W=0.1处裂纹面位移的关系，如图7所示。

将裂纹面区段均布应力值σ和权函数表达式(3)代入式(8)，便能确定所对应的点位移加载条件下的应力强度因子K，结果如图8所示。图8 表明，基于权函数法得到的结果和GB/T 15970.6—2007[4]公式计算结果符合良好，最大差别为1.9% (当a/W=0.3，即l/h=2)。

图7 DCB试样在d/W=0.1处裂纹面位移加载下的无量纲区段均布应力

Fig.7 Normalized segment uniform stresses when DCB specimen subjected to crack surface displacement loading at location of d/W=0.1

图8 DCB试样在d/W=0.1处裂纹面位移加载下的无量纲应力强度因子

Fig.8 Normalized stress intensity factors when DCB specimen subjected to crack surface displacement loading at location of d/W=0.1

根据图8中利用权函数计算得到的无量纲应力强度因子结果，拟合了DCB试样在d/W=0.1处裂纹面位移加载下的应力强度因子公式为

(11)

4 由裂纹嘴位移确定DCB试样在点位移加载下的应力强度因子

按照国家标准GB/T15970.6—2007[4]，利用DCB试样测定材料的应力腐蚀开裂门槛值(KISCC)，只能通过测量裂纹面上d/W处的位移u(a/W,x/W=d/W)，根据式(10)来计算应力强度因子。但是裂纹面的位移，除裂纹嘴位置(试样端部x/W=0)能够很方便地通过位移规准确测量外，其他都是很难准确得到的。本文利用Wu和Carlsson权函数法求得DCB试样的权函数，基于裂纹嘴位移即可确定DCB试样在裂纹面位移加载情况下的应力强度因子，如图9所示，这将为试验中的位移加载参数的准确测量带来很大方便。根据权函数计算结果，拟合得到了高精度的应力强度因子公式，如式(12)所示。利用式(12)，就可以根据位移规对裂纹嘴位移的自动化精确测量结果求得DCB试样的应力强度因子。

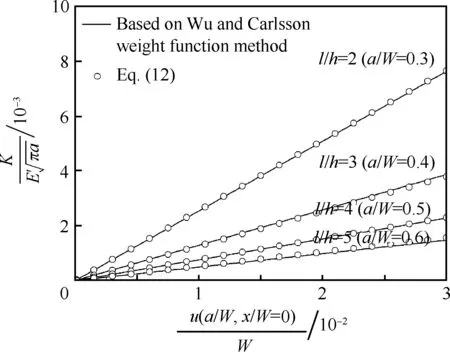
图9 基于裂纹嘴位移确定DCB试样在点位移加载下的无量纲应力强度因子(式(12)与权函数解的比较)

Fig.9 Determination of normalized stress intensity factor based on crack mouth displacements for DCB specimen subjected to point displacement loading (Comparison of Eq.(12) and weight function solutions)

(12)

5 结 论

1) 根据Wu和Carlsson权函数方法，首次给出了双悬臂梁试样的宽范围高精度权函数解析表达式，相应的格林函数得到了Jing和Wu的复变函数泰勒级数展开方法结果的验证。

2) 根据DCB试样的权函数和裂纹面任意位置的位移，求解了在特定位置位移加载情况下的应力强度因子，并与GB/T15970.6—2007的公式作了对比，计算结果符合良好，最大差别为1.9%。

3) 提出了利用裂纹嘴位移反算应力强度因子的方法和DCB试样在特定位置的裂纹面位移加载条件下的应力强度因子与裂纹嘴位移之间的关系。克服了在国家标准GB/T15970.6—2007中，利用双悬臂梁试样测定应力腐蚀开裂门槛值KISCC时，必须通过测量螺栓中心点的裂纹面位移来求解应力强度因子的弊端，为采用这种试样的材料损伤容限性能评价，特别是KISCC的高精度自动化测定奠定了基础。

[1] DIETZEL W, SRINIVASAN P B, ATRENS A. Testing and evaluation methods for stress corrosion cracking (SCC) in metals[J]. Stress Corrosion Cracking: Theory and Practice, 2011: 133-166.

[2] HU J, LUO R S, YAO C K, et al. Effect of annealing treatment on the stress corrosion cracking behavior of SiC whisker reinforced aluminum composite[J]. Materials Chemistry and Physics, 2001, 70(2): 160-163.

[3] 金蕾, 蔡力勋. 基于双悬臂梁试样的柔度方法[J]. 机械强度, 2011, 33(4): 534-537. JIN L, CAI L X. Compliance method based on double cantilever beam[J]. Journal of Mechanical Strength, 2011, 33(4): 534-537 (in Chinese).

[4] 中华人民共和国国家质量监督检验检疫总局，中国国家标准化管理委员会. 金属和合金的腐蚀 应力腐蚀试验 第6部分: 恒载荷或恒位移下预裂纹试样的制备和应用： GB/T 15970.6—2007[S]. 北京: 中国标准出版社, 2007: 181-206. General Administration of Quality Supervise, Inspection and Quarantine of the people’s Republic of China, Standardization Administration of the People’s Republic of China. Corrosion of metals and alloys—Stress corrosion testing—Part 6: Preparation and use of pre-cracked specimens for tests under constant load or constant displacement： GB/T 15970.6—2007[S]. Beijing: China Standards Press, 2007: 181-206 (in Chinese).

[5] BUECKNER H F. Novel principle for the computation of stress intensity factors[J]. Zeitschrift Fuer Angewandte Mathematik & Mechanik, 1970, 50(9): 529-546.

[6] RICE J R. Some remarks on elastic crack-tip stress fields[J]. International Journal of Solids and Structures, 1972, 8(6): 751-758.

[7] WU X R, CARLSSON A J. Weight functions and stress intensity factor solutions[M]. Oxford: Pergamon Press Ltd., 1991: 1-38.

[8] WU X R. Analytical wide-range weight functions for various finite cracked bodies[J]. Engineering Analysis with Boundary Elements, 1992, 9(4): 307-322.

[9] FETT T, MUNZ D. Stress intensity factors and weight functions[M]. Davis, CA: Computational Mechanics Publications, 1997: 289-291.

[10] COURTIN S, GARDIN C, BEZINE G, et al. Advantages of the J-integral approach for calculating stress intensity factors when using the commercial finite element software ABAQUS[J]. Engineering Fracture Mechanics, 2005, 72(14): 2174-2185.

[11] JING Z, WU X R. Wide-range weight functions and stress intensity factors for arbitrarily shaped crack geometries using complex Taylor series expansion method[J]. Engineering Fracture Mechanics, 2015, 138: 215-232.

童第华 男， 博士, 高级工程师。主要研究方向： 疲劳与断裂力学。

Tel: 010-62496725

E-mail: tongdi133@163.com

吴学仁 男， 博士， 研究员， 博士生导师， 中国航空工业集团公司资深首席技术专家。主要研究方向： 断裂力学与疲劳、 损伤容限技术、 材料的力学行为。

Tel: 010-62458003

E-mail: xueren.wu@gmail.com

Received： 2015-03-06； Revised： 2015-05-11； Accepted： 2015-05-27； Published online： 2015-06-29 13:49

URL： www.cnki.net/kcms/detail/11.1929.V.20150629.1349.001.html

Foundation item： National Natural Science Foundation of China (11402249)

*Corresponding author. Tel.： 010-62458033 E-mail: xueren.wu@gmail.com

Weight function method of determining double cantilever beam specimen stress intensity factor by crack mouth displacement

TONG Dihua, WU Xueren*, LIU Jianzhong

AVICBeijingInstituteofAeronauticalMaterials,Beijing100095,China

Double cantilever beam (DCB) specimen has important applications in materials’ damage tolerance properties evaluation, especially for experimental determination of the stress corrosion cracking threshold (KISCC). Because of the particular specimen geometry, crack surface displacement loading at a specific position which is a certain distance away from the specimen edge (crack mouth) is commonly used. However, displacement measurement at the loading position is not only time-consuming but also inaccurate. For the DCB specimen, the most convenient and accurate displacement measurement location is at the crack mouth. In this paper, through finite element calculations for a reference load case and by using the classical weight function method for the edge crack geometry, analytical weight function for the DCB specimen is developed. Comparisons and verification have been conducted using the complex variable function Taylor series expansion weight function. Furthermore, from the specific loading point displacement, stress intensity factor for uniform stress loading at the corresponding crack surface location is obtained by inverse calculation. An analytical expression between the stress intensity factor and the crack mouth displacement is derived for DCB specimen subjected to the crack surface displacement loading at specific position. Thus, a solid foundation is laid for the evaluation of materials’ damage tolerance properties using the DCB specimen, especially forKISCCmeasurement automation with high accuracy.

double cantilever beam specimen; weight function; displacement loading condition; stress intensity factor; crack mouth displacement

2015-03-06；退修日期：2015-05-11；录用日期：2015-05-27； < class="emphasis_bold">网络出版时间：

时间： 2015-06-29 13:49

www.cnki.net/kcms/detail/11.1929.V.20150629.1349.001.html

国家自然科学基金 (11402249)

.Tel.： 010-62458033 E-mail: xueren.wu@gmail.com

童第华， 吴学仁， 刘建中． 由裂纹嘴位移确定双悬臂梁试样应力强度因子的权函数解法[J]． 航空学报, 2016, 37(2): 609-616. TONG D H, WU X R, LIU J Z. Weight function method of determining double cantilever beam specimen stress intensity factor by crack mouth displacement[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(2): 609-616.

http://hkxb.buaa.edu.cn hkxb@buaa.edu.cn

10.7527/S1000-6893.2015.0154

V215

： A

： 1000-6893(2016)02-0609-08

*