时序数据的周期模式发现算法的递推改进

黄雄波

(佛山职业技术学院 电子信息系,广东 佛山 528000)

时序数据的周期模式发现算法的递推改进

黄雄波

(佛山职业技术学院 电子信息系,广东 佛山 528000)

从时序数据中识别和提取出周期成分对掌握事物的内在发展规律有着重要的现实意义。在谐波分析法的基础上，提出了一种具有纳新机制的时序数据周期模式的递推发现算法。该算法通过对谐波分析法的傅里叶系数作Taylor级数的展开，得到了一系列相关的幂函数多项式，在此基础上，基于矩阵数量乘法的规则，将这些多项式解耦为可递推的表达式，进而推导出一种重复计算量极少的递推算法。数值实验验证了算法的有效性和稳定性，而且该算法在计算成本和计算精度之间还具有良好的伸缩性。

时序数据;周期模式;谐波分析法;递推

0 引 言

时序数据就是将某一事物现象在不同时刻上的不同取值，按照时间的先后顺序排列而成的序列。一般地，时序数据可分解为趋势项、周期项及随机项三种成分。其中，趋势项反映了事物的长期动态过程，周期项反映了事物有规则的重复性变动，而随机项是属于具有一定统计规律的无规则变化[1-2]。受地球绕太阳公转以及地球本身自转等原因，自然界的事物普遍具有周期特性，据此，从时序数据中识别和提取出周期成分对掌握事物的内在发展规律有着重要的现实意义。

时序数据周期分析的主要任务就是从已有序列中确定周期项的周期长度，并以相关的周期函数加以定量描述。现有的时序数据周期分析方法主要有方差分析、相关分析、谐波分析、小波分析和周期图分析等方法[3]。近年来，众多专家学者对时序数据的周期模式发现问题展开了研究，并取得了一系列的成果[4-10]。

鉴于现有的周期模式发现算法均不具有递推机制，文中在谐波分析法的基础上，设计实现了一种具有纳新机制的时序数据周期模式的递推发现算法。实验结果及分析表明，该算法具有较高的计算性能，该算法在计算成本和计算精度之间还具有良好的伸缩性。

1 相关基础知识

1.1 时序数据的基本模式

时序数据Yt(t=1,2,…,n)的基本结构模式有加法模式、乘法模式和混合模式3种，如式(1)。

(1)

式中，Ht为趋势项；Pt为周期项；Xt为随机项。

若时序数据的周期项和随机项均不随着趋势项的增长(衰减)而加剧(减弱)变化，则可选用加法模式来描述时序数据，反之，应选用乘法模式，而混合模式则适用于仅有周期项或随机项紧随趋势项变化的场合。

时序数据的建模过程一般为：把序列数据分解为趋势、周期和随机三种成分，然后分别对每种成分进行拟合，最后从式(1)中选取某种合适的模式把这三种拟合结果组合在一起，从而得到时序数据的整体建模函数[11-12]。在实际应用中，趋势项、周期项及随机项这三种成分交错在一起，究竟先分离哪种成分要视具体情况而定，较好的做法是根据各种成分在序列中的轻重地位从重至轻依次分离。这里，将着重对周期成分占优的时序数据进行研究。

1.2 谐波分析法

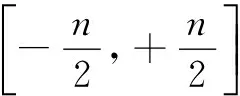
(2)

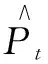
根据最小二乘法和三角函数的正交特性[13]，以得到如式(3)所示的各谐波傅里叶系数求解表达式。

(3)

(4)

又因为

(5)

(6)

(7)

把式(5)～(7)代入式(4)，化简后，有：

(8)

2 周期模式发现算法的递推改进

随着时间的推移，时序数据也面临着数据纳新的问题，即不断地有新的数据补充至原有的序列中。从式(3)中易知，由于各谐波对应的傅里叶系数的求解表达式中均显式地包含序列长度n，因而在数据纳新的过程中，序列长度n不断地在递增变化，这就导致了傅里叶系数需要反复地重新计算。为了有效地提升数据纳新过程中时序数据周期模式发现的计算效能，有必要对式(3)进行递推计算的改进。

2.1 算法的推导

(1)a0分项的递推改进。

记a0(n),a0(n+1)分别为序列长度n及n+1的周期项Pt的平均成分，因为

(9)

故

P1+P2+…+Pn=na0(n)

(10)

而

(11)

把式(10)代入式(11)，便可得到如下所示的递推表达式。

(12)

(2)ai,bi分项的递推改进。

记ai(n)和bi(n)为序列长度n的周期项Pt的傅里叶系数，分别对ai(n),bi(n)求解表达式中的正弦、余弦函数作Taylor级数的展开，并写成矩阵形式。有：

(13)

(14)

根据矩阵数量乘法的规则，式(13)和式(14)可分别化为：

(15)

(16)

η1(n)=[P1+P2+…+Pn],…,ηk+1(n)=[P1+ 22kP2+…+n2kPn]

(17)

μ1(n)=[P1+2P2+…+nPn],…,μk(n)=[P1+22k-1P2+…+n2k-1Pn]

(18)

类似地，记ai(n+1),bi(n+1)为序列长度n+1的周期项Pt的傅里叶系数，又因为

η1(n+1)=η1(n)+Pn+1,…,ηk+1(n+1)=ηk+1(n)+ (n+1)2kPn+1

(19)

μ1(n+1)=μ1(n)+(n+1)Pn+1,…,μk(n+1)=μk(n)+(n+1)2k-1Pn+1

(20)

于是，从式(15)～(20)有：

(21)

从式(21)和式(20)易知，ai(n+1),bi(n+1)虽然不能各自地从ai(n),bi(n)中显式递推，但是可以通过对{η1(n),η2(n),…,ηk+1(n)},{μ1(n),μ2(n),…,μk(n)}中的各个分项进行单独递推，并把各个递推结果与相应的系数项(随序列长度n变化)之积相加，便可快速地求得ai(n+1),bi(n+1),从而也就间接地完成了ai(n),bi(n)到ai(n+1),bi(n+1)之间的递推。

2.2 算法的设计

综上所述，可设计如下的时序数据周期模式的递推发现算法。

输入：时序数据的周期项Pt，Taylor级数的展开项数m，显著周期的判别阈值ε；

输出：时序数据的显著周期项及对应的傅里叶系数ai,bi。

步骤1：按式(9)、式(17)及式(18)计算已有的n项周期序列Pt的a0(n);η1(n),η2(n),…,ηm(n);μ1(n),μ2(n),…,μm(n)；

步骤2：按式(15)、式(16)计算傅里叶系数ai(n),bi(n)；

步骤4：是否继续进行数据的纳新处理？若选择继续，则输入Pn+1，并跳转步骤5；否则跳转步骤6；

步骤5：分别按式(12)、式(19)及式(20)从a0(n);η1(n),η2(n),…，ηm(n);μ1(n),μ2(n),…，μm(n)递推出

a0(n+1);η1(n+1),η2(n+1),…，ηm(n+1);μ1(n+1),μ2(n+1),…，μm(n+1)。以n+1→n,转步骤2；

步骤6：算法结束，输出显著周期成分及其对应的傅里叶系数。

3 实 验

为了验证上述算法的有效性及先进性，文中选取了SIDC(SolarInfluencesDataanalysisCenter)提供的1700年至2000年的平均太阳黑子数来进行周期模式发现的相关实验，实验样本共301个序列数据。实验的硬件环境为惠普ProDesk490G2MT商用台式机(CPU:i5-4570 4*3.2GHz;内存4GB;DDR3 1600)，软件环境及开发工具为Windows8.1+MicrosoftVisualC++2010。实验的主要目的是考察非递推算法与递推算法之间的计算精度及计算效能。

3.1 非递推算法的实验结果

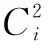
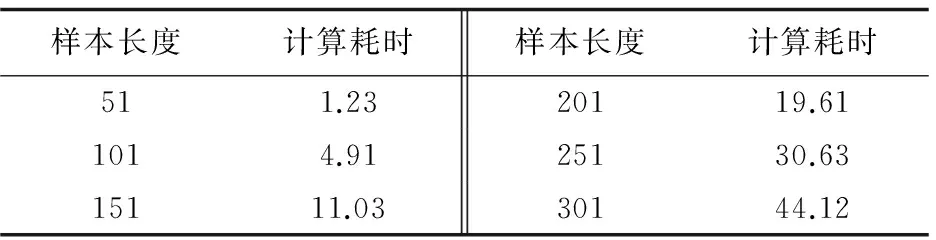
表1 非递推算法的计算耗时 ms

3.2 递推算法的实验结果

应用新设计的递推算法来对上述的太阳黑子数序列进行周期模式发现，并分别用前10项、前15项的Taylor级数进行了2次独立的递推计算，相应的实验结果如表3～5所示(表中m为泰勒级数)。

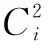
表2 非递推算法所求得的各谐波 成分及其贡献比例

3.3 实验结果分析

由于谐波Ci的角频率为iω0，且ω0=2π/n，故谐波Ci对应的周期Ti=2π/(iω0)=n/i。以表2为例，当样本长度为301时，第30和第27个谐波的贡献最为显著，根据301/30≈10,301/27≈11，故有如下结论：太阳黑子数具有10至11年的活动周期，从表2可知，当样本长度为51、101、151、201及251时上述结论仍然成立，这与其他文献应用别的周期分析方法所得出的结果是相一致的[14]。

对比表2、表4及表5，当取前10项的Taylor级数进行递推计算时，其计算误差随着递推步数的增加而增大，特别是递推至201步后，一些贡献显著的谐波也出现了变更(注：经过计算，发生变更的显著谐波的周期仍然对应着10至11年)；当取前15项的Taylor级数进行递推计算时，贡献显著的谐波成分没有出现变更，在递推至301步时，与非递推的计算结果相比，其计算误差在5%以内。

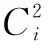
表4 用前10项Taylor级数递推所求得的 各谐波成分及其贡献比例

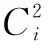
表5 用前15项Taylor级数递推所求得的 各谐波成分及其贡献比例

图1是非递推算法与递推算法(取前15项的Taylor级数)的计算耗时对比示意图。

图1 非递推算法与递推算法的计算耗时对比

综上所述，文中设计的递推算法具有优秀的计算效能及良好的计算精度。

4 结束语

在时序数据的分析与建模过程中，研究相应的递推算法有着重要的现实意义。文中基于谐波分析法，设计实现了一种具有递推计算功能的时序数据的周期模式发现算法。该算法的优点是，在递推过程中可以增加Taylor级数的项数来提高计算精度，而对应的计算耗时却没有显著增加。

为了强调新近数据的作用，渐渐遗忘陈旧数据的影响，下一步的主要工作有：研究带有遗忘因子的时序数据的周期模式的递推发现算法，同时研究有效的积累误差消除方法，以便更好地提升算法的计算精度。

[1]EndersW.应用计量经济学:时间序列分析[M].第3版.北京:机械工业出版社,2012．

[2] 王 燕.应用时间序列分析[M].第3版.北京:中国人民大学出版社,2012．

[3] 郭 龙.时间序列数据的周期性研究[D]．成都:电子科技大学，2013．

[4] 邱敦国，杨红雨.一种基于双周期时间序列的短时交通流预测算法[J]．四川大学学报:工程科学版，2013，45(5):64-68．

[5] 王红瑞，刘达通，王 成，等.基于季节调整和趋势分解的水文序列小波周期分析模型及其应用[J]．应用基础与工程科学学报，2013，21(5):823-836．

[6] 李晓光，宋宝燕，于 戈，等.基于小波的时间序列流伪周期检测方法[J]．软件学报，2010，21(9):2161-2172．

[7]ReschenhoferE，LinglerM.Detectingsynchronouscyclesinfinancialtimeseriesofunequallength[J]．JournalofEmpiricalFinance，2013，24(12):1-9．

[8]WuShujin，ZhuXiaoyu，XiaoYang.Analysisofapproximatelyperiodictimeseries[J]．ChineseJournalofAppliedProbabilityandStatistics，2015，31(2):199-212．

[9]GharehbaghiA，AskP，BabicA.Apatternrecognitionframeworkfordetectingdynamicchangesoncyclictimeseries[J]．PatternRecognition，2015，48(3):696-708．

[10]SuWeiti，PingXiaoou，TsengYi-Ju，etal．Multipletimeseriesdataprocessingforclassificationwithperiodmergingalgorithm[J]．ProcediaComputerScience，2014，37(8):301-308．

[11] 王文举，张桂喜.经济预测、决策与对策[M].第2版.北京:首都经济贸易大学出版社,2013．

[12] 黄雄波.时序数据趋势项的分段拟合[J]．计算机系统应用，2015，24(2):174-179．

[13] 李庆扬，王能超，易大义.数值分析[M].北京:清华大学出版社,2008．

[14] 唐 洁.功率谱分析方法在周期分析中的应用[J]．陕西理工学院学报:自然科学版，2013，29(5):71-74．

Recursive Improvement of Periodic Pattern Algorithm of Time Series Data

HUANG Xiong-bo

(Department of Electronic Information,Foshan Professional Technical College,Foshan 528000,China)

To identify and extract the periodic components from time series data has important practical significance for the inherent rule of things.Based on harmonic analysis method,a periodic pattern recursive algorithm of time series data with renewal mechanism was proposed.A series of power function polynomial is obtained by the expansion in Taylor series of Fourier transform coefficients.On this basis,an simple data algorithm is deduced by polynomial decomposition method on the account of rules of matrix multiplication.The numerical simulation shows that the proposed algorithm is efficient and stable.This algorithm also has good scalability between computing cost and calculation accuracy.

time series data;periodic mode;harmonic analysis method;recursion

2015-05-14

2015-08-18

时间：2016-01-26

广东省科技计划工业攻关项目(2011B010200031)；佛山职业技术学院校级重点科研项目(2011KY006)作者简介：黄雄波(1975-)，男，博士研究生，副教授，CCF会员，研究方向为时间序列分析及数字图像处理。

http://www.cnki.net/kcms/detail/61.1450.TP.20160126.1520.040.html

TP311

A

1673-629X(2016)02-0047-05

10.3969/j.issn.1673-629X.2016.02.011