基于分布式倒排索引的频繁项集挖掘

李雪迪，郑 彦

(南京邮电大学 计算机学院，江苏 南京 210003)

基于分布式倒排索引的频繁项集挖掘

李雪迪，郑 彦

(南京邮电大学 计算机学院，江苏 南京 210003)

频繁项集挖掘是关联规则挖掘中的核心，其直接影响了频繁项集的产生效率。针对Eclat算法在挖掘海量数据中的频繁项集时存在的内存和计算资源不足等问题，文中设计了通过分布式倒排索引实现频繁项集挖掘的DiiEclat算法。倒排索引等同于将数据垂直分布，按事务编号的不同将倒排索引分布式地存储在不同的索引节点上，每个节点上的事务分别做交集，最后由检索代理合并交集结果。在chess、mushroom、T40I10D100K和T10I4D100K数据集上，对DiiEclat、Eclat、Diffset等算法进行了实验对比。结果表明，给出的DiiEclat算法通过事务集合垂直划分和并行计算，解决了数据挖掘过程中求交集运算效率低下和内存不足等问题，算法高效、可扩展。

Eclat算法；频繁项集；倒排索引；并行计算

0 引 言

挖掘频繁项集是生成关联规则的关键。Apriori算法[1]是最有影响的挖掘布尔关联规则频繁项集的算法，但该算法需要多次重复扫描数据库，候选项集的生成效率较低并占用大量内存。对此,J.Han等[2]提出了不产生候选频繁项集的方法—FP-growth算法。尽管FP-growth算法有很多优点，但是它也有不足，动态地生成和释放数以万计的条件FP-树，将耗费大量的时间和空间。

上述两种挖掘算法基于水平数据格式进行挖掘，相比之下Zaki等[3]提出的Eclat算法的数据集采用垂直数据的表示形式。Eclat算法由2个项集的Tidset求交集快速得到候选集的支持度，当频繁项集庞大，进行交操作时会消耗系统大量的内存，影响算法效率。宋长新等[4]提出Eclat+算法，充分利用Apriori的先验性质防止大量的时间消耗在额外候选集的产生及支持度的计算上。Zaki等[5]提出用Diffset垂直数据来减少交集的数据规模，降低内存消耗。为改进频繁项集产生的效率，傅向华等[6]提出基于倒排索引位运算的DF-FIMBII。该算法采取二进制数组位运算可以实现快速求交集，在数据规模非常大，建立倒排索引时，需为每个项目分配一个数组，导致性能下降。张玉芳等[7]结合划分思想和突出基于概率的先验约束方法，通过将事务划分为多个非重叠部分，并对每一部分分别采用Eclat算法，以减少比较次数。冯培恩等[8]提出基于双层哈希表的Eclat_opt算法，提高了剪枝的效率，但双层哈希表需要额外的内存开销。

文中提出了一种基于分布式倒排索引挖掘频繁项集的算法。垂直数据格式的实质就是倒排索引[9]，按事务TID的不同将倒排索引分布式地存储在不同的索引节点上，每个索引节点负责一个TID区间，因此每个索引节点上倒排索引中的TID互不相同。在交叉计数时，将检索请求广播到每个节点，节点并行计算，最后由检索代理合并结果。该算法降低了交集的规模，实现了并行计算，从而提高了挖掘效率。

1 Eclat关联规则挖掘

1.1 关联规则相关概念

假设I={I1,I2,…,In}是项的集合。给定一个交易数据库D，其中每个事务(Transaction)T是I的非空子集，即每一个交易都与一个唯一的标识符TID(TransactionID)对应。关联规则是形如X→Y的蕴涵式，其中X⊂I,Y⊂I且X∩Y=∅。X和Y分别称为关联规则的先导和后继。

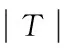
对于关联规则X⟹Y的可信度是指包含X和Y的事务数与包含X的事务数之比，即：confidence(X⟹Y)=support(X⟹Y)/support(X)。可信度反映了如果交易中包含X，则交易包含Y的概率。

1.2 Eclat算法

Eclat算法是一种深度优先算法，采用垂直数据表示形式，在概念格理论的基础上利用基于前缀的等价关系将搜索空间(概念格[10])划分为较小的子空间(子概念格)。各子概念格采用自底向上的搜索方法独立产生频繁项集。

与FP-growth和Apriori算法不同，Eclat算法加入了倒排的思想，具体就是将事务数据中的项作为key，每个项对应的Tidset作为value。项集X和Y可以组成一个新的项集Z，则Z的支持度计数为(X，value)∩(Y，value)。Eclat算法采用此方法计算支持度，对候选k项集进行支持度计算时，不需再次扫描数据库，仅在一次扫描数据库后得到每个1项集的支持度，而候选k项集的支持度就是在对k-1项集进行交集操作后得到该k项集Tidset中元素的个数[11]。

2 基于分布式倒排索引的频繁项集挖掘

倒排索引源于实际应用中需要根据属性的值来查找记录，Eclat算法查找频繁项集是根据项目Item的值来查找事务Tidset求交集的过程，所以文中的索引对象是事务和事务包含的项目。倒排索引包括两个部分：词项词典和倒排记录表。词项是可以被检索的基本单位，索引中为每个词项维护一个倒排记录表。倒排记录表中仅需要采用单链表记录每个项目Item出现的事务TID。当倒排索引占用内存达到一定大小时，才将词典和倒排记录表写入磁盘中。

文中采用分布式倒排索引提高了频繁项集挖掘的效率，将倒排索引按照事务编号垂直划分的shard分布到不同的服务器上，服务器对不同shard并行计算交集，最后合并结果。

2.1 分布式倒排索引

扫描事务数据库，根据TID值作Hash操作去查找Hash值所属的范围，找到对应的shard。每个shard内保存部分索引片段，从而实现分布式的倒排索引。

例如：设项目集I有两个项目I1和I2，I1和I2的事务列表分别为TID(I1)={1,2,4,6,8,9,11,14,15}和TID(I2)={1,3,4,6,7,9,12,13,15}。预设三个shard，分别是shard1、shard2、shard3，其对应的TID范围分别是1～5、6～10、11～15。通过上述条件建立的分布式倒排索引如图1所示。I1,I2对应倒排索引的词项词典，shard1、shard2、shard3对应倒排记录表，里面的记录以单链表形式存储在内存空间。

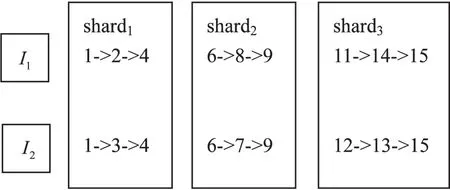
图1 分布式倒排索引(I1,I2)

当求项目I1和I2的交集运算时，shard1、shard2、shard3并行地在每个分片上求和。shard1上交集为{1,4}，shard2上交集为{6,9}，shard3上交集为{15}，最后合并的结果为：{I1,I2}={1,4,6,9,15}，支持度计数为5。虽然倒排索引和Hash结构很相似，但倒排索引不允许存在碰撞，而Hash存在碰撞，因此索引左侧的I1,I2采用Bitmap表示，每个Ii对应一个位置，并且是一一对应的，从而Ii可以被快速定位。索引右侧链表长度由9变为3，降低了内存空间的要求和交集规模，加快了交集运算的速度，同时shard1、shard2、shard3并行计算，进一步提高了交集运算的速度。

根据数据库中事务集T的规模，将事务集T按升序划分，分片范围为shard1(1～Tn1)，shard2(1～Tn2)，…，shardn(1～Tnn)。

2.2 基于分布式倒排索引的频繁项集挖掘算法

建立事务集的分布式倒排索引后，查询统计的效率是非常高的，可以快速得到1-频繁项集。然后采用深度优先搜索策略递归挖掘k-频繁项集，并将得到的k-频繁项集建立新的分布式倒排索引。根据Apriori算法中定义的▷◁ 运算，在挖掘k-项集时利用频繁(k-1)-项集对候选k-项集进行剪枝[12]。▷◁ 运算定义如下：

lk-1中的两个元素l1和l2可以执行连接操作的条件是：

(l1[1]=l2[1]∧l1[2]=l2[2]∧…∧l1[k-2]=l2[k-2]∧l1[k-1]=l2[k-1])

l1和l2连接的结果为：

{l1[1],l1[2],…,l1[k-1],l2[k-1]}

基于分布式倒排索引的频繁项集挖掘算法描述如下：

输入：数据库D，最小支持度阈值minsup；

输出：所有频繁项集L。

(1)第一次扫描数据库，建立分布式倒排索引index1，同时得到频繁1-项集L1，L=L∪L1；

(2)Eclat(Lk)：

forallXi∈Lkdo

forallXj∈Lk，i

若R=Xi∪Xj为k-项集且它的(k-1)-项集在index的Item中可搜索到，则R=Xi∪Xj成为一个新的候选项集。

Tidset(R)=Query(XiANDXj)

若|Tidset(R)|≥minsup，则L=L∪R，indexk=indexk∪R，其中indexk初始为空。

(3)若indexk≠∅，调用函数Eclat(indexk)。

上述基于分布式倒排索引的频繁项集挖掘算法关键是Query(XiANDXj)，数据分片并行求交集后合并。假设一个分片上Xi的链表长度为n，Xj的链表长度为m，则Query(XiANDXj)的时间复杂度为O(m+n)。

每个分片上(XiANDXj)是两个链表求交集的过程，将两个链表求交集后得到的链表直接保存在该分片的内存形成新的倒排索引。例如：I1和I2在shard1上交集得到的链表为1->4，1和4仍然属于shard1，所以直接将其以倒排索引保存在内存中。算法中indexk=indexk∪R是保存新产生的频繁项集的倒排索引。该操作都在各自shard上完成，不需要网络传输开销。

R=Xi∪Xj为k-项集且它的(k-1)-项集在index的Item中可搜索到，则R=Xi∪Xj成为一个新的候选项集。由于倒排索引的词项词典(Item)可以快速定位，因此提高了对候选项集剪枝的效率。比如：由2-项集{I1,I3}和{I2,I3}生成项集3-项集{I1,I2,I3}时，项集{I1,I2}是否频繁在Item中可以快速查询，从而可以对候选集{I1,I2,I3}进行剪枝。

3 实 验

3.1 实验环境和实验数据

使用编号1～5的虚拟机搭建基于Solr[13]和Zookeeper[14]的分布式搜索方案SolrCloud实现分布式倒排系统，每台机器上的SolrCore管理一个索引分片shard。所有的事务TID分配到四个shard数据区间上，每个shard的Tidset链表相互独立。每台机器运行的操作系统为CentOS6.3，内存2 G，采用Java语言编程实现文中提出的DiiEclat算法。算法Eclat、Diffset和Eclat_opt用VC++2008实现，运行的平台环境为Win7旗舰版，内存2 G。

实验数据集分为两类：一类是稀疏型合成数据集T40I10D100K和T10I4D100K；另一类是密集型实际数据集chess和mushroom。

3.2 实验结果与分析

实验过程分为两步：第一步，单机DiiEclat算法与算法Eclat、Diffset、Eclat_opt，针对不同数据集选择不同的minsupport运行时间对比；第二步，DiiEclat算法在minsupport相同时，不断增加shard节点个数，得到四种数据集运行时间的变化趋势。

第一步的实验结果如图2～5所示。

图2 chess上四种算法的运行时间结果

图3 mushroom上四种算法的运行时间结果

chess和mushroom同为事务数较少的密集数据集，Diffset算法由于采用差集操作在数据集稠密时效率比Eclat算法高。而对事务数目较大的稀疏数据集T10I4D100K和T40I10D100K，Diffset算法明显效率降低，不如Eclat算法。文中提出的DiiEclat算法通过Apriori算法的性质和倒排表的快速定位Item大大提高了剪枝效率，无论数据集的稠密程度如何，效率明显优于算法Diffset和Eclat。Eclat_opt算法在四个数据集上都有较高的效率，但其通过双层哈希表以空间换取时间，当数据集或者项目数变大时，额外的内存开销是比较大的，以至于单机内存条件无法承受。而DiiEclat算法通过将索引段分布式存储，既能并行计算交集、减少链表长度，又降低了每个节点的内存需求。

图4 T40I10D100K上四种算法的运行时间结果

图5 T10I4D100K上四种算法的运行时间结果

第二步的实验结果如图6所示。DiiEclat算法针对四种数据集选取不同的minsupport，同时根据第一步的实验结果选取运行时间较长的minsupport，即chess(60)、mushroom(10)、T40I10D100K(0.4)和T10I4 D100K(0.05)。

随着节点个数由1增加到5，DiiEclat算法在数据集chess(60)、mushroom(10)、T40I10D100K(0.4)和T10I4D100K(0.05)的运行时间均明显减少。随着节点个数N的增加，使得求交集的链表长度L平均降到L/N，两个链表求交集的时间和每个节点上的内存需求明显降低。同时，由于几个节点并行求交集，进一步加快了算法的效率。

4 结束语

文中提出了一种基于分布式倒排索引的深度优先频繁项集挖掘算法。垂直数据格式的实质是倒排索引，基于分布式倒排索引的DiiEclat算法挖掘频繁项集时，通过将索引垂直划分后分配到不同的节点上并行计算，解决了内存和计算资源不足等问题。DiiEclat算法通过节点扩展能够有效挖掘大数据集的频繁项集。在下一步工作中，将考虑调整分布式倒排索引的存储结构，进一步提高所提方法的性能。

[1]AgrawalR,ImielinakiT,SwamiA.Miningassociationrulesbetweensetsofitemsinlargedatabases[C]//ProcoftheACMSIGMODconferenceonmanagementofdata.Washington,D.C.:ACM,1993:207-216.

[2]HanJ,PeiJ,YinY.Mingfrequentpatternswithoutcandidategeneration[C]//Procofthe2000ACMdata.Dallas,UnitedStates:ACM,2000:1-12.

[3]ZakiMJ.Scalablealgorithmsforassociationmining[J].IEEETransactionsonKnowledgeandDataEngineering,2000,12(3):372-390.

[4] 宋长新,马 克.改进的Eclat数据挖掘算法的研究[J].微计算机信息,2008,24(24):92-94.

[5]ZakiMJ.Fastverticalminingusingdiffsets[R].NewYork,USA:RensselaerPolytechnicInstitute,2001.

[6] 傅向华,陈冬剑,王志强.基于倒排索引位运算的深度优先频繁项集挖掘[J].小型微型计算机系统,2012,33(8):1747-1751.

[7] 张玉芳,熊忠阳,耿晓斐,等.Eclat算法的分析及改进[J].计算机工程,2010,36(23):28-30.

[8] 冯培恩,刘 屿,丘清盈,等.提高Eclat算法效率的策略[J].浙江大学学报:工学版,2013,47(2):223-230.

[9] 郑榕增,林世平.基于Lucene的中文倒排索引技术的研究[J].计算机技术与发展,2010,20(3):80-83.

[10]DaveyBA,PriestleyHA.Introductiontolatticesandorder[M].Cambridge,UK:CambridgeUniversityPress,1990.

[11] 陆 楠.关联规则的挖掘及其算法的研究[D].长春:吉林大学,2007.

[12] 徐章艳,刘美玲,张师超,等.Apriori算法的三种优化方法[J].计算机工程与应用,2004,40(36):190-192.

[13]KucR.ApacheSolr3.1cookbook[M].[s.l.]:PacktPublishing,2001.

[14] 黄毅斐.基于ZooKeeper的分布式同步框架设计与实现[D].杭州:浙江大学,2012.

Frequent Itemset Mining Based on Distributed Inverted Index

LI Xue-di，ZHENG Yan

(College of Computer,Nanjing University of Posts and Telecommunications,Nanjing 210003,China)

Mining frequent itemsets is the core of mining association rules,which directly affects the efficiency of generating frequent itemsets.Eclat algorithm exists issues of insufficient memory and computing resource when mining frequent itemset of massive data.The DiiEclat algorithm is proposed for mining frequent itemsets through distributed inverted index.Inverted index is equal to the vertical distribution of the data,and according to the number of different transactions inverted index will be distributed on different index nodes,each node calculates the intersection of transactions on itself,the results of the intersection merged by the retrieval agent.The execution time of DiiEclat,Eclat,Diffset and Eclat_opt is compared in four datasets such as chess,mushroom,T40I10D100K and T10I4D100K.The experimental results show that DiiEclat is given to improve efficiency of intersection operation through the vertical division of the transaction sets and parallel computing,and it is efficient and scalable.

Eclat algorithm;frequent itemset;inverted index;parallel computing

2015-01-16

2015-04-20

时间：2016-02-18

国家“863”高技术发展计划项目(2006AA01Z201)

李雪迪(1989-)，男，硕士研究生,研究方向为数据挖掘、大数据、云计算；郑 彦，教授，硕士生导师，研究方向为数据挖掘、信息安全。

http://www.cnki.net/kcms/detail/61.1450.TP.20160218.1619.002.html

TP311

A

1673-629X(2016)03-0101-04

10.3969/j.issn.1673-629X.2016.03.024