根定系数的三种类型

根定系数的三种类型

□毕 燕 左久刚

分式方程的“三根”是指分式方程的有根、无根（无解）和增根.利用分式方程的“三根”情况，确定分式方程的系数，不仅是近年中考的热点题型，也是难点和棘手的问题.本文通过对近两年的300多套中考题的筛选，选择出了下列最有代表性的三例，进行解答和剖析，目的是使同学们对这部分问题做到胸中有数.

一、有根定系数——分母不为零

分式方程有根是指分式方程有正根、负根、非正根、非负根等，均称为有根，通过有根的条件，确定方程的系数的范围.但是要注意隐蔽的条件：分式方程有根，分式方程的分母不能为零.

A.m＞2B.m＜2

C.m＞－2D.m＜－2

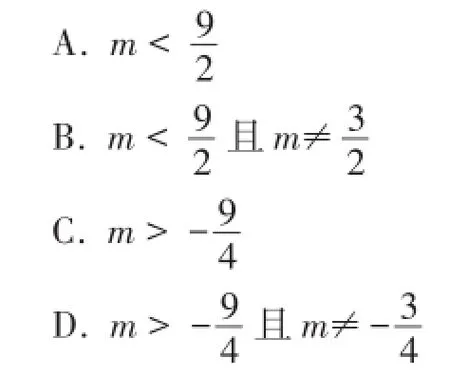
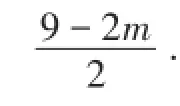
又因为x－3≠0，所以x≠3，

故选择B.

点评：解有关含有字母（非方程的未知数）的分式方程时，首先考虑用题目中含有的字母的代数式（如本题中的m）表示方程的解，然后根据题目的条件确定字母的取值范围.解答时要注意字母的取值不能使分式方程产生增根.由分式方程有根确定系数时，不仅要考虑其根的正数、负数条件等，还要考虑其分母不为零.忽视了分母为0的隐含条件，就会出现取值范围扩大的错误，所以必须牢记分母不为零.

二、增根定系数——分母必为零

如果分式方程有增根，这个增根一定使某个分母为零，所以使分母为零是确定方程有增根的必选条件.

A.m＝－1B.m＝0

C.m＝3D.m＝0或m＝3

解析：（1）方程两边都乘以最简公分母（x－3），把分式方程化为整式方程，再根据分式方程的增根就是使最简公分母等于0的未知数的值求出x的值，然后代入进行计算即可求出m的值.

方程两边都乘以（x－3），

得2－x－m＝2（x－3），

∵分式方程有增根，

∴x－3＝0，解得x＝3，

∴2－3－m＝2（3－3），

解得m＝－1.故选A.

（2）把a当已知数求出方程的根，根据方程的增根是1，确定a的值.

方程两边都乘（x－1），

得ax＋1－x＋1＝0，

（a－1）x＝－2，

点评：根据分式方程的增根，确定方程的系数，首先把分式方程转化为整式方程.然后使原分式方程的分母为零，求出其增根.再将增根代入整式方程，确定方程的系数.注意：使分母为零，是解决有增根问题的关键.

三、“无根”定系数——注意“两个数”

分式方程无解有两种情形：一是将原分式方程两边都乘以最简公分母，约去分母得到整理后的整式方程为ax＝b，此时若a＝0，且b≠0，则此整式方程无解，当然原分式方程无解；二是化分式方程为整式方程后，此整式方程的解是原分式方程增根，当然分式方程也无解.

A.－5B.－8 C.－2D.5

解析：（1）去分母得3x－2＝2x＋2＋m，由于分式方程无解，故x＋1＝0，即x＝－1.将x＝－1代入3x－2＝2x＋2＋m，解得m＝－5.故选择A.

（2）去分母得x－a＝ax＋a，

整理得（1－a）x＝2a.

由于分式方程无解，所以有两种情况：

①分母为0，即x＝－1，所以a－1＝2a，解得a＝－1；

②整式方程无解，即1－a＝0，解得a＝1.

综上所述a＝±1.

点评：分式方程无解可能是解这个分式方程后，得到的根都是原分式方程的增根，所以原分式方程没有解；也可能是把分式方程转化为整式方程后，这个整式方程无解，导致分式方程无解.所以解答这类问题，必须考虑两点，解题才是完整的.