基于鲁棒优化的发电商电量分配策略

周洁，赵琛，张少华

(上海市电站自动化技术重点实验室(上海大学自动化系)，上海市 200072)

基于鲁棒优化的发电商电量分配策略

周洁，赵琛，张少华

(上海市电站自动化技术重点实验室(上海大学自动化系)，上海市 200072)

电力工业的市场化改革可为发电商提供多种交易选择，由于各种交易选择的收益风险特性不同，发电商需要合理分配交易电量以达到满意的风险收益目标。首先，针对现货市场电价的不确定性，采用鲁棒利润和条件鲁棒利润，来描述回避风险的发电商在一定置信水平下的确保利润；然后，提出发电商在现货市场、双边合同和期权等交易选择中的电量分配鲁棒决策模型，通过该模型获得的电量分配策略，可使发电商在一定置信水平下使其确保的利润最大化，并可对风险承受程度不同的发电商制定不同的电量分配策略；最后，通过算例证明了模型的合理性和有效性。

电力市场；电量分配；条件鲁棒利润；风险管理

0 引 言

电力工业的市场化改革可为发电商提供多种交易选择。发电商可以通过现货市场进行电能交易，也可以通过双边合同和期权合同售电。通常，现货市场交易价格波动激烈，而双边合同和期权交易的价格相对稳定。由于各类交易选择的收益风险特性不同，发电商需要通过风险管理方法，在各个交易选择中合理分配交易电量，以达到满意的风险收益目标[1]。

传统风险管理方法主要包括方差模型[2]、风险价值(value at risk,VaR)和条件风险价值(conditional value at risk，CVaR)方法[3]等。这些方法均在一定风险约束条件下，追求最大化期望收益，并获得期望最优策略。实际中由于大多数发电商具有回避风险的特性，因而在电量分配决策时可能更关心不确定性因素对自身收益带来的最不利影响，并尽量避免这一最坏情况所带来的后果(最差收益)，换言之，发电商的电量分配策略所追求的目标是最差收益尽可能大，这一目标可借助鲁棒优化来实现。

鲁棒优化是一种解决不确定性问题的强有力工具，其是以最坏情况为优化目标，得到的优化方案不一定最优，但当参数发生变化时，仍能确保优化方案的可行性，使优化方案对不确定性参数波动不敏感[4-5]。目前鲁棒优化理论已应用于电力系统规划、调度等多个领域。文献[6-7]采用场景鲁棒优化方法解决了电力系统多时段不确定性优化调度问题；文献[8-9]针对风电的不确定性，在鲁棒优化理论基础上，采用盒式不确定集合表示风速的不确定性，建立了基于盒式鲁棒优化的风电场最大装机容量模型；文献[10-11]考虑电价不确定性，并假设电价属于椭球不确定集，建立了以电厂售电利润为目标函数的机组优化模型；文献[12]在现货市场电价不确定的情况下，运用鲁棒优化方法建立了一种在约束发电商报价参数下获得最大利润的优化模型。上述鲁棒优化的方法都存在共同的局限性：(1)不确定性只考虑约束参数端点的变化；(2)随机参数的分布是对称的，而且没有利用概率分布信息；(3)只考虑最坏情况下的目标，并没有全面考虑决策者的风险偏好特性。

针对上述问题，本文运用基于概率的鲁棒优化理论，考虑现货市场电价不确定性，采用鲁棒利润(robust profit, RP)和条件鲁棒利润(conditional robust profit, CRP)[13]，来描述回避风险的发电商在一定置信水平下的确保利润，建立发电商在现货市场、双边合同和期权等交易选择中的电量分配鲁棒优化模型，并给出模型的求解方法。最后，通过算例证明模型的合理性和有效性。

1 基于鲁棒优化的发电商电量分配

受现货市场电价不确定性的影响，风险规避型发电商在电量分配决策时最关心的是在满足一定的置信水平下，使最坏情况下的利润尽可能最大。

1.1 鲁棒利润和条件鲁棒利润

记B(x,λ)为发电商利润函数，其中x为决策变量，λ为随机变量，在发电商电量分配问题中，决策变量x表示发电商在各个市场中的电量分配，随机变量λ表示不确定的现货市场电价。设p(λ)为随机变量λ的概率密度函数，则发电商利润B(x,λ)不少于临界值α的概率可表示为

ψ(x,α)=∫B(x,λ)≥αp(λ)dλ

(1)

对给定的置信水平β∈(0,1)，发电商的鲁棒利润定义为

RPβ(x)=max{α∈R:ψ(x,α)≥β}

(2)

式中RPβ表示发电商的利润不小于临界值α的概率大于等于给定的置信度水平β时，发电商可能获得的最大确保利润。

鲁棒利润的实质为：发电商的利润不小于临界值α的概率时，发电商利润的一个下分位点值。然而，其并没有考察到利润小于分位点时所包含的情况。为了克服RPβ的不足，定义条件鲁棒利润：

(3)

从式(3)可以看出：积分域B(x,λ)≤RPβ(x)为利润函数小于RPβ的区域，其出现的概率为1-β。故CRPβ是指利润小于RPβ的期望值。RPβ和CRPβ的示意图如图1所示[9]。

图1 RPβ和CRPβ的示意图Fig.1 Graphical representation of RPβ and CRPβ

1.2 基于鲁棒优化的发电商电量分配模型

1.2.1 发电商电量分配一般模型

一般以发电商的收益函数作为目标函数：

C(p)=ap2+bp+c

(5)

式中：a、b、c分别为发电商的二次、一次、常数成本系数；p为发电商发电出力。

约束条件：

(1)发电商出力约束：

pmin≤p≤pmax

(6)

式中pmin和pmax分别表示发电商出力的最小、最大值。

(2)双边合同l签订的最大最小电量约束：

(7)

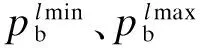
(3)发电商在双边合同、看跌期权及现货市场中售电总和等于发电商出力，即

(8)

1.2.2 基于鲁棒优化的发电商电量分配模型

由于电价的不确定性会影响发电商的利润，发电商最关心的是某一置信水平的最差收益，此时发电商收益可以保证不小于此最差值。鲁棒利润只解决了一定置信水平下最差收益的最大值，但是它对尾部损失的测量不充分，使得发电商对收益的掌握不确切，其可能小于实际的收益，这种看似很小的差别可能会带来巨大的损失，而条件鲁棒利润考虑了发电商的实际利润低于鲁棒利润的情况，所以目标函数为最大化发电商条件鲁棒利润：

maxinfB(q,λs,β)

(9)

infB(q,λs,β)=CRPβ(q)

(10)

式中B(q,λs,β)为置信水平为β时，发电商的利润函数，CRPβ(q)的积分中含有RPβ(q)项，而RPβ(q)的解析表达式难以求出。引入一个相对简单的辅助函数代替CRPβ(q)：

(11)

式中[B(q,λs)-α]-=min{B(q,λs)-α,0}。

由式(13)推导可知：

CRPβ(q)=maxGβ(q,α)

(12)

假设ψ(q,α)连续，则有

maxGβ(q,α)=Gβ[q,RPβ(q)]=RPβ(q)+

{1-ψ[q,RPβ(q)]}=RPβ(q)+CRPβ(q)-

(13)

(14)

则

(15)

因此，目标函数转化为

(16)

(17)

另外增加如下约束条件：

(18)

zk≤0

(19)

2 算例仿真

假设现货市场某1小时时段的预测电价服从均值为41.6/(MW·h)，标准差为4.160/(MW·h)的对数正态分布，即logλs～N(41.6,4.162)，利用蒙特卡罗方法模拟1 000组电价离散样本。发电商成本函数的系数为：a=0.004 8/(MW·h)2，b=16.19/(MW·h),c=1 000.0。发电机组最大、最小出力为455，150 MW。

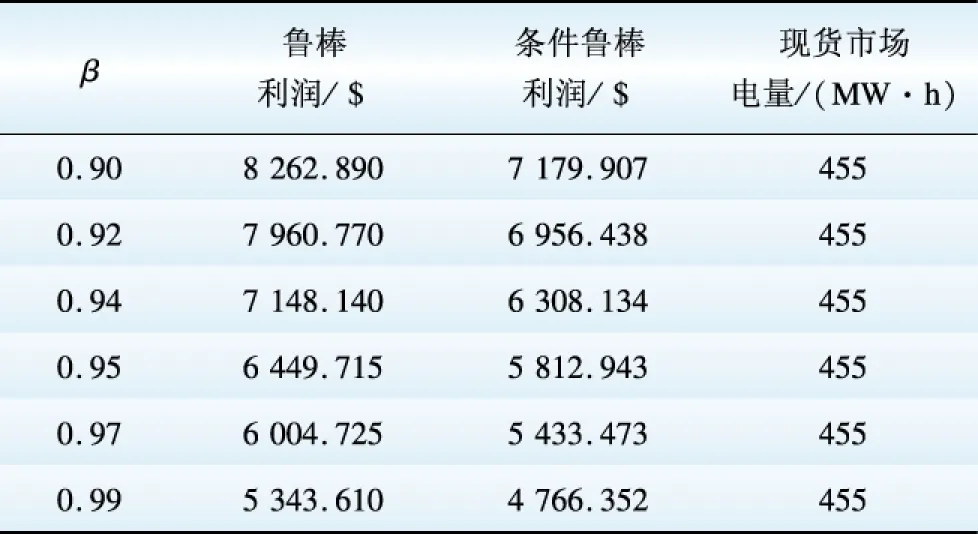
情况1：假设发电商只在现货市场销售电能。表1给出了不同置信水平下的优化结果。从表1可以看出，置信水平β越大，表明发电商对风险的承受程度越小，β=0.90时，发电商对风险规避程度最小，β=0.99时，发电商对风险规避程度最大；当β=0.99时，RPβ为6 449.715 $，CRPβ为5 812.943 $。CRPβ的值小于RPβ的值。说明发电商有5%的可能性利润低于6 449.715 $，且利润低于6 449.715 $时,可能获得的平均利润下降到5 812.943 $。随着置信水平的增加，可能获得的利润下降。

表1 不同置信水平下的优化结果(情况1)
Table 1 Optimal results under different c onfidence levels Case 1

情况2：假设发电商在双边合同、看跌期权和日前现货市场间销售电能。看跌期权敲定价格λc为36.3$/(MW·h)，权利金价格λ0为1.648$/(MW·h)。发电商可选售电的5个双边合同参数如表2所示。表3给出了不同置信水平下的优化结果。图2给出了发电商鲁棒利润和条件鲁棒利润随置信水平的变化曲线。图3给出了在不同的置信水平下，发电商在不同市场中的电量分配调度结果。

表2 情况2中双边合同参数
Table 2 Bilateral contracts parameters in Case 2

表3 不同置信水平下的优化结果(情况2)Table 3 Optimal results under different confidence levels (Case 2)

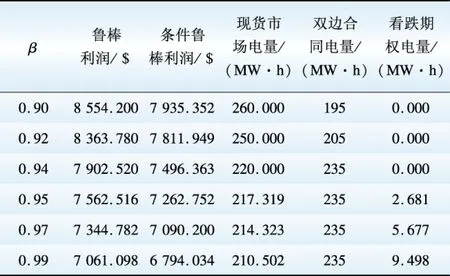
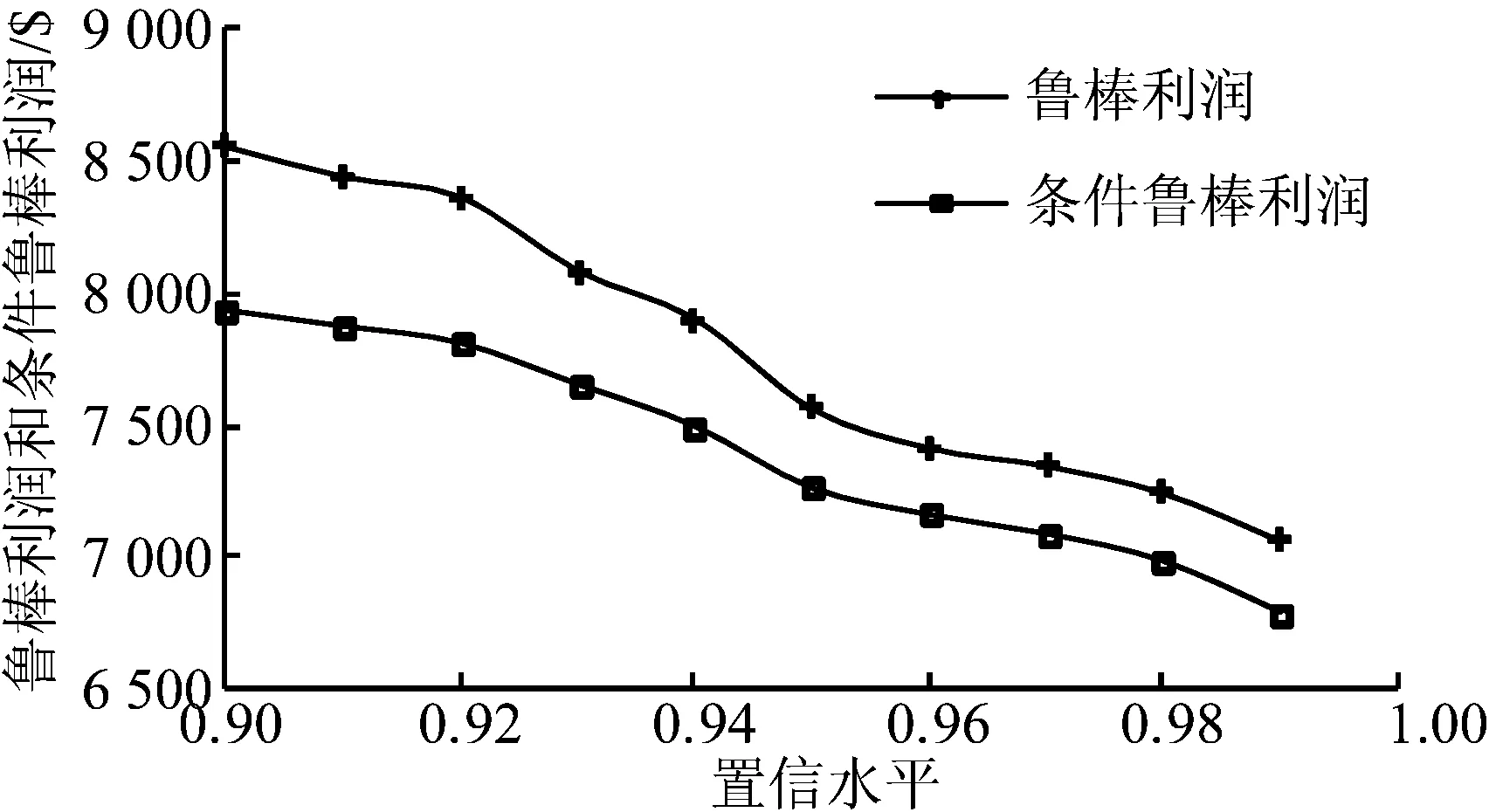
图2 RP和CRP与置信水平的关系(情况2)Fig.2 Relationship of RP, CRP and confidence levels (Case 2)

图3 不同置信水平下的电量分配策略(情况2)Fig.3 Electricity capacity allocation strategies under different confidence levels (Case 2)

从表3可以看出，当β从0.9增加到0.94时，发电商在现货市场销售的电量份额减少，在双边合同市场销售的电量份额增加；当β从0.95增加到0.99时，发电商在现货市场销售的电量份额继续减少，在双边合同市场销售的电量份额继续增加，当签订的双边合同电量增加到最大值235 MW时，发电商在看跌期权市场销售的电量份额增加。说明随着置信水平的增加，发电商风险规避程度增加，鲁棒利润和条件鲁棒利润减小。发电商希望通过增加双边合同电量和看跌期权电量来规避风险。

现货市场电价的标准差大小反映了其波动性的大小。标准差越大，发电商在现货市场中售电的风险也越大。表4给出了当β=0.95时，决策结果随现货市场电价标准差σ的变化情况。从表4可以看出，当电价标准差σ增加时，发电商的鲁棒利润及条件鲁棒利润减小，且其会选择增加看跌期权电量，来规避现货市场的价格风险。

3 结 论

本文采用鲁棒利润和条件鲁棒利润，来描述回避风险的发电商在一定置信水平下的确保利润，建立了发电商在现货市场、双边合同和期权等交易选择中的电量分配鲁棒决策模型。由该模型获得的电量分配策略，可使发电商在一定置信水平下使其确保的利润最大化，并可对风险承受程度不同的发电商制定不同的电量分配策略。算例仿真表明了模型和方法的合理性和有效性。

表4 不同现货市场电价标准差下的决策结果(情况2)
Table 4 Results for different standard deviations of spot price (Case 2)

[1]周娟，江辉，李鹏.基于WCVaR风险度量的发电商电量分配模型[J].电力系统及其自动化学报，2012，24(1)：156-160. ZHOU Juan， JIANG Hui， LI Peng. Optimization portfolio allcation for generation companies based on worst-case conditional value-at-risk[J]. Proceeding of the CSU-EPSA，2012，24(1)：156-160.

[2]MATHURIA P， BHAKAR R， LI F.GenCo’s optimal power portfolio selection under emission price risk[J].Electric Power Systems Research，2015，121(3)：279-286.

[3]周任军， 刘志勇， 闵雄帮，等.不确定性优化方法在电力系统研究中的应用[J].电力科学与技术学报， 2014，29(2)：21-29. ZHOU Renjun， LIU Zhiyong， MIN Xiongbang， et al. A review on application of uncertainty optimization method in power systems[J].Journal of Electric Power Science and Technology，2014，29(2)：21-29.

[4]谢鹏， 彭春华， 于蓉.大规模间歇式电源接入电网多目标鲁棒优化调度[J].电网技术，2014，38(6)：1479-1484. XIE Peng， PENG Chunhua， YU Rong. Multi-objective robust optimized scheduling of power grid connected with large-scale intermittent power sources[J]. Power System Technology，2014，38(6)：1479-1484.

[5]BEN-TAL A， NEMIROVSKI A.Robust optimization methodology and applications[J].Mathematical Programming， 2002，92(3)：453-480.

[6]JEYAKUMAR V， LI G Y， SRISATKUNARAJAH S.Strong duality for robust minimax fractional programming problems[J].European Journal of Operational Research， 2013，228(2)：331-336.

[7]杨明， 韩学山， 王士柏，等.不确定运行条件下电力系统鲁棒调度的基础研究[J].中国电机工程学报， 2011，31(S1)：100-107. YANG Ming，HAN Xueshan，WANG Shibo，et al.Fundamental research for power system robust dispatch under uncertain operating condition[J].Proceedings of the CSEE，2011，31(S1)：100-107.

[8]李斯， 周任军， 童小娇，等.基于盒式集合鲁棒优化的风电并网最大装机容量[J].电网技术， 2011，35(12)：208-213. LI Si， ZHOU Renjun， TONG Xiaojiao， et al. Robust optimization with box set for maximum installed capacity of wind farm connected to grid[J].Power System Technology，2011，35(12)：208-213.

[9]梅生伟， 郭文涛， 王莹莹，等.一类电力系统鲁棒优化问题的博弈模型及应用实例[J].中国电机工程学报， 2013，19(19)：47-56. MEI Shengwei， GUO Wentao， WANG Yingying， et al.A game model for robust optimization of power systems and its application[J].Proceedings of the CSEE，2013，19(19)：47-56.

[10]LUO X， CHUANG C Y， YANG H， et al.Robust optimization-based generation self-scheduling under uncertain price[J].Mathematical Problems in Engineering，2011， 18(4)：264-265.

[11]LIU S， JIAN J， WANG Y， et al.A robust optimization approach to wind farm diversification[J].International Journal of Electrical Power & Energy Systems，2013， 53(4)：409-415.

[12]陈洋洋.基于鲁棒凸优化方法的发电商在现货市场和远期市场的投标策略[J].长沙理工大学学报(自然科学版)， 2010，7(1)：57-63. CHEN Yangyang. Bidding strategy of robust convex optimization based on the spot market and forward market[J].Journal of Changsha University of Science and Technology(Natural Science)，2010，7(1)：57-63.

[13]JABR R A.Robust self-scheduling under price uncertainty using conditional value-at-risk[J].IEEE Trans on Power Systems，2005，20(4)：1852-1858.

[14]魏传江，王浩，姜新民，等.GAMS用户指南[M].北京：中国水利水电出版社，2009. WEI Chuanhao，WANG hao，JIANG Xinmin， et al. GAMS user’s guide[M].Beijing： China Water Conservancy Hydropower Press，2009.

[15]BROOKE A， KENDRICK D.MEERAUS A.GAMS user’s guide[M].Redwood City： The Science Press，1990.

(编辑 张小飞)

Electricity Capacity Allocation Strategies of Generation Companies Based on Robust Optimization

ZHOU Jie, ZHAO Chen, ZHANG Shaohua

(Key Laboratory of Power Station Automation Technology, Department of Automation, Shanghai University, Shanghai 200072, China)

In the marketization reform of power industry, the generation company (Genco) can sell electricity power through several trading choices. These trading choices have different risk-return characteristics, so the Genco should allocate the electricity among these trading choices reasonably to achieve a satisfactory risk-return target. Firstly, according to the uncertainty of spot market price, this paper uses the robust profit (RP) and conditional robust profit (CRP) to define the Genco’s guaranteed profit under a certain confidence level. Then, we propose a robust decision model for Genco’s electricity capacity allocation among the spot market, bilateral contract and option contract. The electricity capacity allocation strategies obtained through this model can maximize the Genco’s guaranteed profit under a certain confidence level, and make different allocation strategies for Gencos with different attitudes toward risk. Finally, the rationality and validity of the model are proved by a numerical example.

electricity market; electricity capacity allocation; conditional robust profit; risk management

上海市自然科学基金项目 (14ZR1415300)

TM 73

A

1000-7229(2016)03-0058-05

10.3969/j.issn.1000-7229.2016.03.009

2016-01-25

周洁(1989)，女，硕士研究生，主要研究方向为电力市场风险管理；

赵琛(1988)，女，博士研究生，主要研究方向为电力市场风险管理、博弈分析等；

张少华(1966)，男，博士，教授，主要研究方为向电力市场风险管理、需求响应和博弈分析等。

Project supported by Natural Science Foundation of Shanghai Municipality (14ZR1415300)