阶梯电价下居民峰谷分时电价测算优化模型

赵会茹, 王玉玮, 张超, 舒艳, 赵名锐

(华北电力大学经济与管理学院, 北京市 102206)

阶梯电价下居民峰谷分时电价测算优化模型

赵会茹, 王玉玮, 张超, 舒艳, 赵名锐

(华北电力大学经济与管理学院, 北京市 102206)

为了在现有居民阶梯电价的基础上设计峰谷分时电价，使两种价格相结合，从而进一步引导居民合理用电，提高能源效率，提出一套阶梯电价下居民峰谷分时电价测算优化模型与方法。首先，按现行各档阶梯电价的用户覆盖范围，将全体居民户分为相对应的各子群体细分市场；其次，构造各子群体细分市场的分时电价需求响应函数并建立相应的峰谷分时电价优化目标函数集；再次，在各子群体细分市场内构建峰谷分时电价约束条件集；最后，联合目标函数及约束条件，形成各细分市场的峰谷分时电价优化模型，模型的输出结果，即为对应各阶梯的最优峰谷分时电价。算例仿真验证了模型的合理性与可行性，敏感性分析进一步揭示了各阶梯最优峰谷电价结果随需求响应变化的规律。

阶梯电价; 峰谷分时电价; 居民用户; 细分市场; 优化模型

0 引 言

为解决工业用电和居民用电交叉补贴等问题[1]，在我国大部分地区，自2012年以来，便开始实行居民阶梯式递增电价，通过分段电量实现细分市场的差别定价，从而在一定程度上提高了能源的利用效率。从电价结构上看，这样的阶梯价格大都并未进行峰谷分时定价，即任一阶梯的电价都是一个不随时段变化而存在差异的统一价格。这样一来，该价格体系便无法在调整居民负荷曲线形状特点等方面起到进一步优化用电行为的作用。另一方面，随着我国居民生活用电比重不断提高，电网负荷曲线正不断呈现出新的变化。为了提高电网的供电可靠性、电能质量和电网负荷率，引导居民用户电力消费，有必要针对居民群体不同时段的负荷特点，在已实施的居民阶梯电价基础上制定峰谷分时电价，从而达到调节电网高峰低谷负荷、改善系统负荷曲线、削峰填谷、缓解电力紧张、提高负荷率、提高电网安全性和经济性以及增强电力系统的运行效率和稳定性等目的。因此，研究如何在现有阶梯电价的基础上制定居民峰谷分时电价，从而综合利用两种价格体系在提高能源利用效率等方面的作用，必将成为一项同时具有理论创新与工程实践意义的热点问题。

近年来，在国内外相近领域研究中所取得的许多进展，均可为研究阶梯电价下居民峰谷分时电价的制定问题提供有益借鉴。例如，文献[1-3]等分别从各类用户的历史电价与负荷数据出发，运用各种数学及计算机方法建立需求响应模型，从而预测出各类用户在峰、平、谷各时段的用电负荷随峰谷分时电价的变动而变化的需求响应规律，这为科学建立峰谷分时电价优化决策模型提供了计量基础；文献[4-6]等分别从理论与工程实践等角度，提出建立各类用户的峰谷分时电价测算优化模型均应以最大限度地对负荷曲线“削峰填谷”为优化目标；文献[7]将售电侧峰谷分时电价对负荷曲线的“削峰填谷”效果与发电侧节约化石燃料程度相联系，建立了描述从峰谷分时电价制定到发电侧节能减排效应的需求侧响应垂直传导机制；文献[8]等在上述研究进展的基础上，进一步从环境保护角度出发，建立了峰谷分时电价联动定价体系，在垂直一体化的电力系统交易模式下，将发电侧与售电侧电价均调整为峰谷分时电价；文献[9]提出了针对上海、江苏等地区先有居民峰谷分时电价的情况下，如何进一步制定阶梯电价，从而为本文模型的构建提供了较有价值的借鉴与启发。

然而，截至2015年，虽然我国一些省份已就关于在阶梯电价基础上，如何制定居民峰谷分时电价这一问题展开试点或立项研究(例如2014年11月4日，河北省物价局发布《关于扩大居民用电峰谷分时电价试点范围的通知(冀价管[2014]第123号)》，随后相关部门在石家庄市内部分居民小区开展居民阶梯峰谷电价试点工作等)，但均未形成具体的价格决策机制及政策建议。国内外关于居民阶梯峰谷分时电价测算理论的研究更为鲜有。华东地区部分省市目前所实施的居民峰谷阶梯电价，是在已有居民峰谷分时电价的基础上进一步实施阶梯电价所形成的，虽然在最终实施效果上，先峰谷后阶梯与先阶梯后峰谷并无差别，但由于历史上两种价格体系优先制定的顺序不同，阶梯电价基础上居民峰谷分时电价测算的理论模型与方法无法照搬前者，需要根据具体情况，在合理借鉴的基础上建立科学的数学模型与测算方法。

本文立足于对如何建立在阶梯电价基础上，居民峰谷分时电价测算优化模型的问题进行研究。模型构建的具体思路与步骤将在下一小节中展开。算例仿真进一步验证了本文所建模型的科学性与可行性。在算例仿真的最后，文章又就各细分市场居民对峰谷分时电价需求响应规律在一定范围内的变动，对最终输出的最优电价结果进行了相应的敏感性分析，进而从风险估计角度揭示了各阶梯最优峰谷电价结果随需求响应变化的规律。

1 模型技术路线

本文构建在阶梯电价基础上的居民峰谷分时电价测算优化模型的基本思路为：

首先，将所有居民用户进行分类。由于我国大部分地区现行的居民阶梯电价分为3个梯档，第1梯档单位居民户用电量的设置以绝大部分居民的日常所需为出发点，特别是低收入人群；第2梯档单位居民户用电量的设置主要考虑满足正常合理用电需求的居民，电价逐步调整到弥补电力企业正常合理成本并获取合理收益的水平；第3梯档单位居民户用电量的设置主要考虑较高生活质量需求的用户，电价提高到在弥补成本和获取收益的基础上，适当加入环境损害成本。因此，本文按照阶梯电价的分档思路将居民用户进行分类，将某地区第1梯档阶梯电价实施范围内的所有居民用户标记为第1类子群体细分市场；将第2梯档阶梯电价实施范围内的所有居民用户标记为第2类子群体细分市场；将第3梯档阶梯电价实施范围内的所有居民用户标记为第3类子群体细分市场。

其次，对各子群体细分市场分别构建峰谷分时电价需求响应模型，求出各子群体细分市场内用电负荷对峰谷分时电价变化的平均响应规律。

再次，分别针对各类子群体细分市场建立峰谷分时电价优化模型的目标函数集以及约束条件集，并在此基础上完成各子群细分市场所对应的峰谷分时电价测算优化模型的构建。

最后，各子群体模型输出的最优解即为所对应各阶梯的峰谷分时电价测算值。

综上所述，图1是阶梯电价下峰谷分时电价测算优化模型的技术路线。

2 阶梯电价下居民峰谷分时电价需求响应函数

由于各类子群体细分市场的用户在收入、生活习惯等方面存在显著差异，而这些均是影响用户峰谷分时电价需求响应的重要因素[3]。因此，应单独分析各子群体细分市场中居民用户对峰谷分时电价的平均需求响应规律。

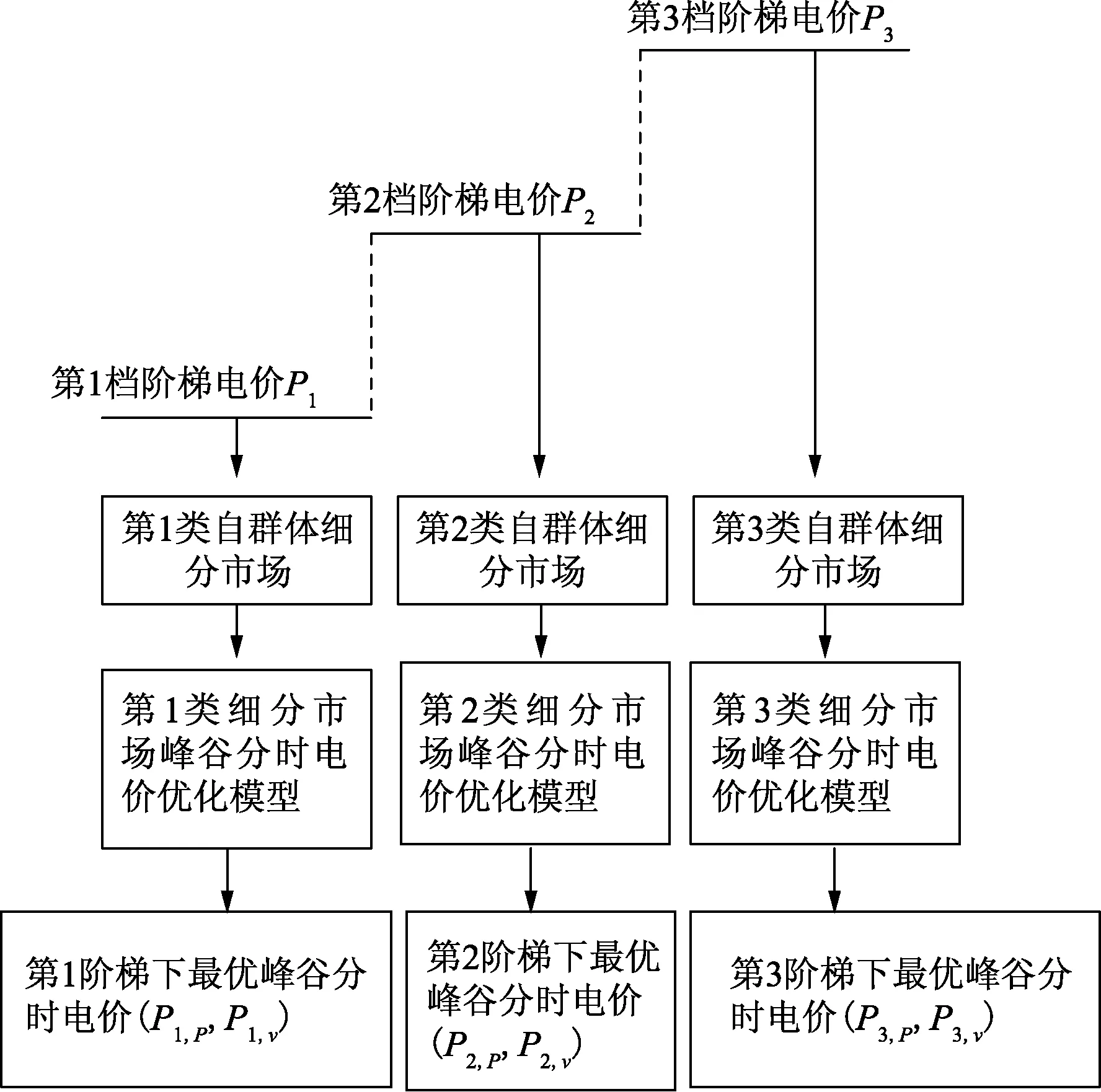
图1 阶梯电价下峰谷分时电价的技术路线Fig.1 Technical route of TOU tariff under multi-step electricity price

借鉴华东地区经验，假设所研究地区已针对居民用电负荷曲线的形状特点对该地区居民用电的峰(p)、谷(v)两时段进行划分。并设在该地区内，第i(i=1,2,3)档电价阶梯所对应的第i类子群体细分市场内居民p、v各时段用电负荷与峰谷分时电价的近似数值关系[3]可表示为：

(1)

(2)

(3)

式(3)中具体参数的确定方法可参见文献[2]等。

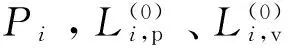
3 阶梯电价下居民峰谷分时电价测算优化模型构建

在确定了各类用户的需求响应函数之后，便可针对各类子群体用户需求响应特点分别建立对应的各电价阶梯上的峰谷分时电价测算优化模型。

(1)目标函数集确定

实施峰谷分时电价的最终目的是通过改变用电负荷曲线的形状来最大程度地节约各种社会成本[8]。因此，本文所建优化模型的目标函数集应包含以下2个目标元素[5-8]：

Obi={objecti(1),objecti(2)}

(4)

上式表示第i类子群体(对应于第i档电价阶梯)峰谷分时电价测算优化模型的目标函数集。其中：

目标函数objecti(1)表示最大限度地降低p时段负荷

(5)

目标函数objecti(2)表示最大限度地降低p、v时段负荷差

(6)

(2)约束条件集确定

在构建峰谷分时电价优化模型时，必须同时考虑到一些必要的约束条件，以确保最终目标的合理实现。根据文献[3-8]，本文确定在构建第i类子群体(对应于第i档阶梯电价)峰谷分时电价测算优化模型的约束条件集可表示为

(7)

1)conditioni(1)价格约束

为保证用户利益不受损害，峰谷分时电价备选方案实施后，居民的平均购电价格不增加

(8)

式中，Tp、Tv分别表示所研究周期内p、v各时段的时长。

2)conditioni(2)时段约束

实施峰谷分时电价后，p、v时段不能倒置，即满足

Li,v≤Li,p

(9)

公式(9)的意义在于，用户对峰谷分时电价进行需求响应后，p时段的平均负荷不应低于v时段，否则p、v各时段将不再具有实际意义，而应重新进行划分，优化目标实现的效果也会受到一定程度的抵消(即由于此时的峰荷与谷荷在时间分布上发生了转移，原本可消除的负荷峰谷差依然存在)。

3)conditioni(3)成本约束

各时段电价应当满足不低于某个下限值Pd，该下限值是根据电力系统供电成本所设定的

Pi,t≥Pd,∀t=p,v

(10)

4)conditioni(4)电量约束

为保证原有各档阶梯电价的用户覆盖范围在阶梯峰谷电价下不发生显著改变，各阶梯实施峰谷分时电价后，用户在整个分析周期内的户均总用电量不能超过相应的阶梯分档电量

(11)

式中：Ni为第i类子群体细分市场的居民户数量，Qi为第i当阶梯电价的人均分档电量上限。

联合式(5)、(6)、(8)、(9)、(10)、(11)便可得到对应于第i档阶梯电价的峰谷分时电价测算优化模型：

(12)

(13)

4 模型求解

根据多目标优化的常见处理方法[10]，可将上述2条比选原则按如下方法进行处理，从而使得双原则比选问题化简为单原则比选问题：

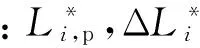
(2)考虑当objecti(1)和objecti(2)的重要性相当，可在两者之间平均分配权值，于是，objecti(1)和objecti(2)可转化为如下单目标问题：

(14)

上式即为经处理后的峰谷分时电价综合优化目标函数。

5 算例仿真

5.1 数据准备

经调查，我国某北方城市现行的居民阶梯电价为：第1档电价0.49元/(kW·h)，第2档电价 0.54元/(kW·h)，第3档电价0.79元/(kW·h)。其中，第1档阶梯电价覆盖了该地区80%左右的居民户，第2档阶梯电价覆盖了15%左右的居民户，第3档阶梯电价覆盖了5%左右的居民户。

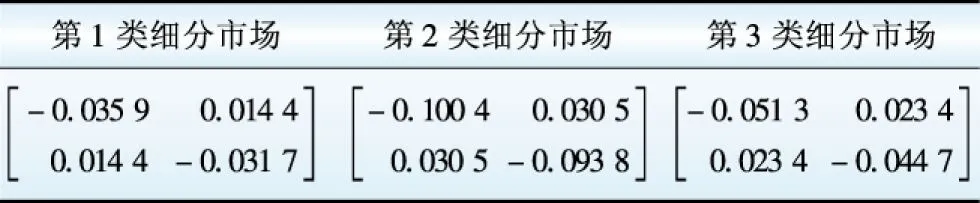
本文以该市2014年居民用户负荷资料作为仿真的数据来源。数据样本包含该市收入高、中、低档居民小区按比例共22 541户居民户(此数据为经过筛选后的有效数据)，每户在全年365日都拥有全天各时点的负荷值。在该地区阶梯电价电量分档要求的基础上，进一步将年用电量大于4 800kW·h的居民户划分为第3类子群体，共1 083户；年用电量小于2 640kW·h的居民户分为第1类子群体，共18 631户；年用电量介于两者之间的居民户分为第2类子群体，共 2 827户。通过在上述3类子群体中分别选取一定数量的典型用户进行调研，并在结合上海市等其他已实施居民峰谷两时段电价地区的历史数据的基础上，估算出各子群体细分市场的电量电价弹性矩阵数值，如表1所示。

表1 细分市场弹性矩阵表
Table 1 Elasticity matrix of segment market

另外，根据对该地区电力系统供电成本的考虑，设定谷时段电价下限为0.307元/(kW·h)。

5.2 结果分析

将所获取的各类数据进行处理，得到各子群体中式(5)、(6)、(8)、(9)、(10)、(11)中相关参数的取值。运用Matlab R2014a软件编辑粒子群算法程序，对优化模型进行求解。3类子群体细分市场优化模型的输出结果对应于3档阶梯电价下最优的峰谷分时电价，其具体结果见表2。

为了显示表3中所列出的各梯档最优峰谷分时电价在对用户负荷曲线“降低峰荷”、“削峰填谷”等方面的效果，下表中将该电价体系与未经过峰谷分时调价的原始阶梯电价进行比较(用户样本集上的比较)。

表2 最优阶梯峰谷电价结果
Table 2 Optimal multi-step TOU tariff results 元/(kW·h)

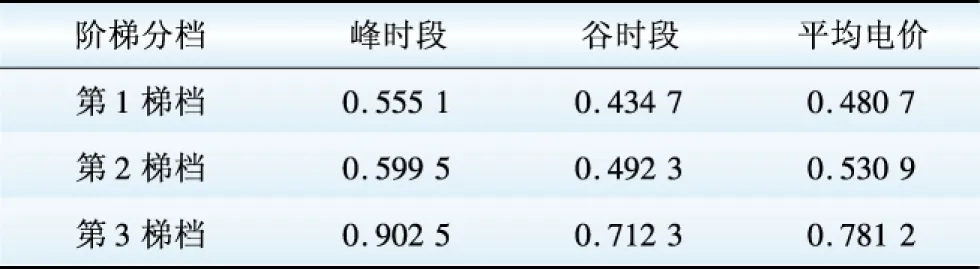
表3 分时电价实施效果对照表Table 3 Comparison of implementation effect of TOU tariff

分析表2、3可知：(1)3段阶梯在实施峰谷分时电价后，其平均电价水平均维持在各自现行的阶梯电价附近(如表3所示)，最大浮动量仅为 0.009 3元/(kW·h)。这说明，从平均水平上看，实施峰谷分时电价并未严重改变原有的阶梯电价水平与结构，从而保证了峰谷分时后的各阶梯价格对该地区居民用户的覆盖率不会发生明显改变，现行阶梯电价体系所发挥的各项作用不会因各阶梯合理进行峰谷分时调价而丧失。(2)就每一阶梯内的电价而言，峰谷分时调价前后负荷峰谷差等指标得到了一定程度的改善(如表4所示)，即各阶梯峰谷分时电价起到了对负荷曲线“降低峰荷”、“削峰填谷”等作用。(3)若将模型中的双目标函数改为负荷峰谷差最小化(或峰荷最小化)单目标函数，则模型所输出的各阶梯峰谷分时电价能够起到更好的“削峰填谷”(或“降低峰荷”)效果。综上所述，在阶梯电价的基础上合理设定峰谷分时电价，能够在保障充分发挥原有阶梯电价各项作用的同时，有效改善相应各子群体细分市场内用户的负荷曲线形状，从而进一步达到提高电网的供电可靠性、电能质量和电网负荷率，引导居民用户合理消费电力等目的。

5.3 敏感性分析

(1)关于居民峰谷分时电价需求响应弹性

考虑到我国居民用电需求弹性研究缺乏历史数据累积，因此，通过用户调研及与其他省市历史数据相对比，所预测的各子群体细分市场居民户的电量电价弹性矩阵数值必然存在一定程度的误差。因此，有必要针对各细分市场居民对峰谷分时电价响应规律在一定范围内的变动，对最终输出的最优电价体系结果进行单因素敏感性分析(以epp、epv单独变动为例进行分析)。

对表4分析可知，(1)对于自弹性epp而言，其取值越低模型输出的各阶梯最优方案中峰谷价格差就越小，反之则越大，即峰谷价格差与自弹性取值成单调递增关系；(2)对于交叉弹性epv而言，其取值越低模型输出的各阶梯最优方案中峰谷价格差就越大，反之则越小，即峰谷价格差与交叉弹性取值成单调递减关系(见图2-3)。

从以上两图的比较中还能看出，阶梯峰谷分时电价对自弹性epp的变动反应更为敏感。

(2)关于目标函数的权重

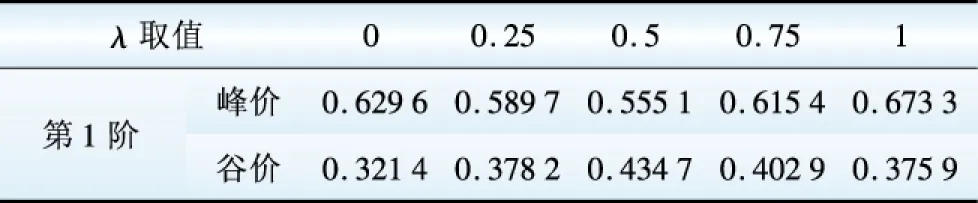
前文对双目标函数单一化处理的方法是在所形成的综合目标函数中，对2个优化目标均赋予1/2的权重。然而，在实际操作中，价格制定者可以根据自身需要，灵活调整在2个优化目标之间的权重分配。设赋予目标函数式(5)的权重为λ(λ∈[0 1])，表5给出了以第1档阶梯分时电价为实例的敏感性分析结果。

表4 需求响应敏感性分析
Table 4 Sensitivity analysis of demand response元/(kW·h)

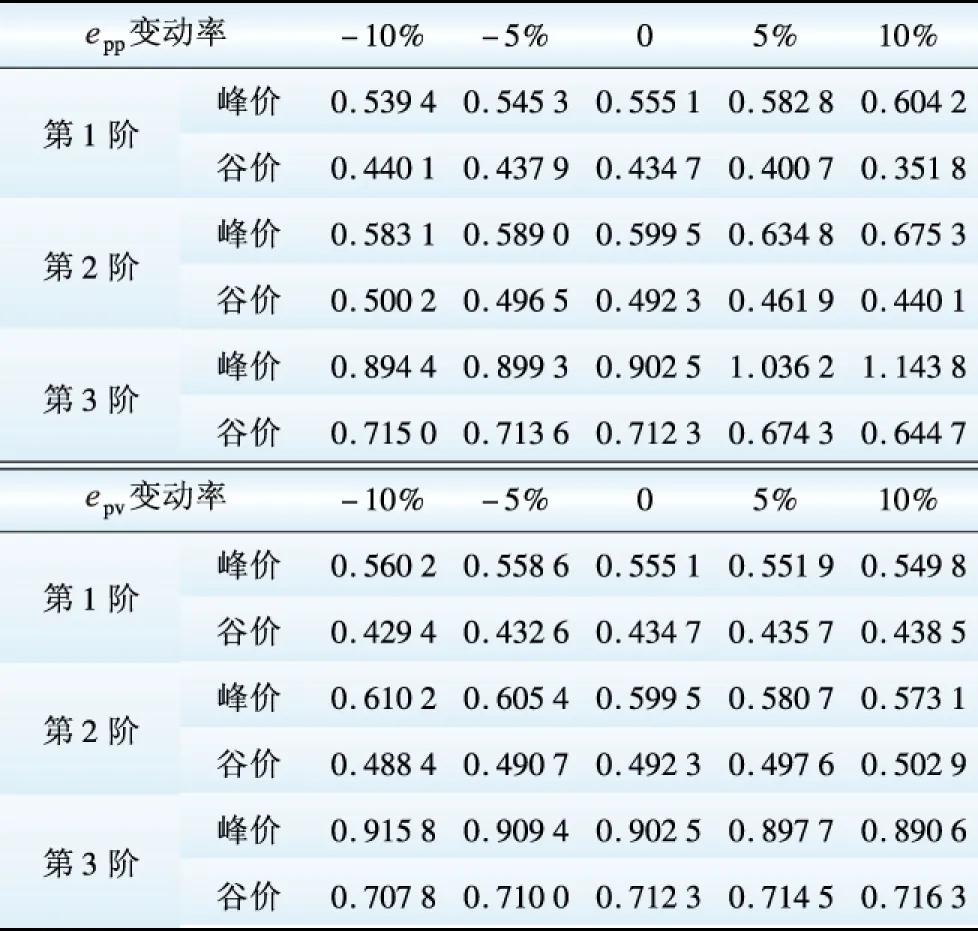
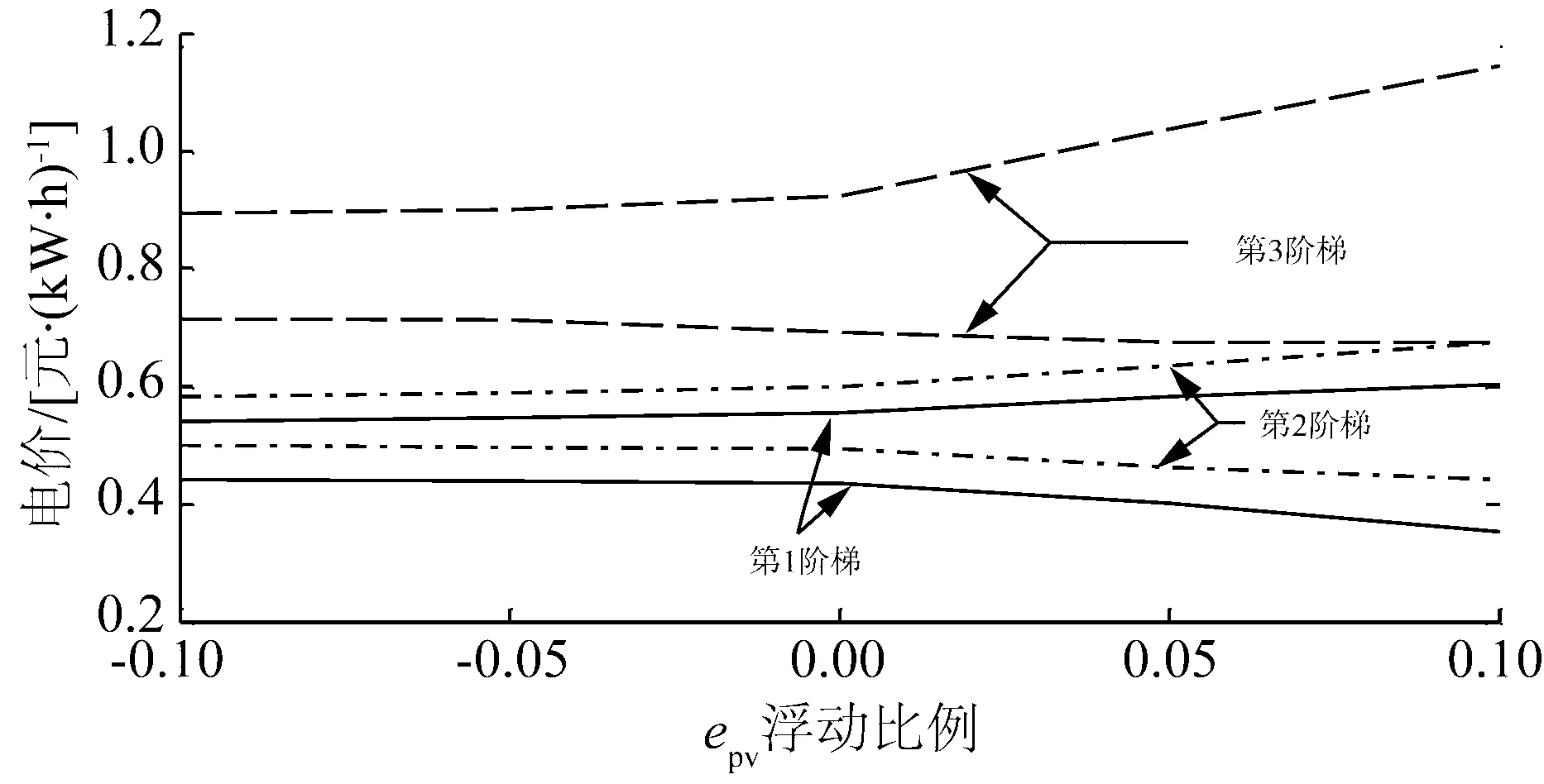
图2 自弹性敏感性分析图Fig.2 Self-elasticity sensitivity analysis

图3 交叉弹性敏感性分析图Fig.3 Cross-elasticity sensitivity analysis

表5λ敏感性分析
Table 5 Sensitivity analysis ofλ元/(kW·h)

6 结 论

(1)在原有阶梯电价的基础上，将居民用户划分为相对应的各子群体细分市场，并在各细分市场上建立优化模型来求解各阶梯下最优峰谷分时电价的理论方法是合理可行的。只要在模型中合理地设定目标函数与约束条件，便能在保证发挥原有阶梯电价解决价格交叉补贴，提高能源利用效率等作用的基础上，进一步通过峰谷分时电价的设定来实现优化居民用电负荷曲线形状、削峰填谷、缓解电力紧张、提高负荷率、提高电网安全性和经济性以及增强电力系统的运行效率和稳定性等目的。

(2)从敏感性分析中可以看出，用户的需求响应规律对合理测算各阶梯最优峰谷分时电价至关重要。在缺乏用户需求峰谷电价弹性历史数据的情况下，必须要通过对相应居民用户群体的大样本调研来获取相对真实的响应数据。此方面更进一步的研究请参阅文献[1-3]等。

(3)本文所构建的模型方法亦可推广到解决在阶梯电价的基础上设计峰、平、谷3时段分时电价的问题中来。从实施效果上看，无论先阶梯再峰谷定价，还是先峰谷再阶梯定价并无明显差异。但比对本文模型与文献[9]中的方法可知，两种价格制定的先后顺序不同，会导致具体模型过程的显著差异。因此，本文所建立的模型方法对指导我国大部分地区(这些地区已实施了居民阶梯电价，但价格并未峰谷分时)的相关价格制定工作具有十分重要的借鉴意义。

[1]阮文骏, 王蓓蓓, 李扬, 等. 峰谷分时电价下的用户响应行为研究 [J]. 电网技术, 2012, 36(7)：86-93. RUAN Wenjun, WANG Peipei, LI Yang, et al. Customer response behavior in time-of-use price[J]. Power System Technology, 2012, 36(7)：86-93.

[2]辛洁晴, 程浩忠.电力需求短期分时价格弹性的特性及其应用[J].电力系统自动化, 2007, 31(10)：32-35. XIN Jieqing, CHENG Haozhong. Properties of short-term TOU price elasticities of electricity demand and their application[J].Automation of Electric Power Systems, 2007, 31(10)：32-35.

[3]刘继东, 韩学山, 韩伟吉.分时电价下用户响应行为的模型与算法[J].电网技术, 2013, 37(10)：2973-2978. LIU Jidong, HAN Xueshan, HAN Weiji. Model and algorithm of customers’ responsive behavior under time-of-use price[J].Power System Technology, 2013, 37(10)：2973-2978.

[4]张丽英, 谭忠富, 王绵斌, 等. 考虑不确定响应的分时电价分级优化模型[J]. 中国管理科学, 2009,17(1), 50-57. ZHANG Liying, TAN Zhongfu, WANG Mianbin, et al. The classification optimization model of time-of-use price considering consumers’ uncertain responses[J]. Chinese Journal of Management Science, 2009,17(1): 50-57.

[5]FLORIAN K, PETER A C I, ANDERSSON G O R.Valuing investments in multi-energy conversion, storage, and demand-side management systems under uncertainty[J].IEEE Transactions on Sustainable Energy, 2011, 2(2): 194-202.

[6]陈沧杨, 胡博, 谢开贵, 等. 计入电力系统可靠性与购电风险的峰谷分时电价模型[J]. 电网技术, 2014, 38(8), 2141-2148. CHEN Cangyang, HU Bo, XIE Kaigui, et al. A peak-valley TOU price model considering power system reliability and power purchase risk[J]. Power System Technology, 2014, 38(8): 2141-2148.

[7]谭忠富, 于超, 姜海洋. 用户端峰谷分时电价对发电端节煤影响分析模型[J]. 系统工程理论与实践, 2009, 29(10): 94-103. TAN Zhongfu, YU Chao, JIANG Haiyang. Analysis model on the impact of user TOU electricity price on generation coal-saving[J]. Systems Engineering—Theory & Practice, 2009, 29(10): 94-103.

[8]谭忠富, 陈广娟, 赵建保, 等. 以节能调度为导向的发电侧与售电侧峰谷分时电价联合优化模型[J]. 中国电机工程学报, 2009, 29(1): 55-62. TAN Zhongfu, CHEN Guangjuan, ZHAO Jianbao, et al. Optimization model for designing peak-valley time-of-use power price of generation side and sale side at the direction of energy conservation dispatch[J]. Proceedings of the CSEE, 2009, 29(1): 55-62.

[9]黄海涛. 居民分时阶梯电价联合优化模型研究[J]. 电网技术, 2012, 36(10): 253-261. HUANG Haitao. A joint optimization model of residential time-of-use block electricity rate[J]. Power System Technology, 2012, 36(10): 253-261.

[10]徐永丰,吴洁晶,黄海涛,等. 考虑负荷率的峰谷分时电价模型[J]. 电力系统保护与控制,2015,43(23):1-9. XU Yongfeng, WU Jiejing, HUANG Haitao, et al. Time-of-use tariff model considering load factor[J]. Power System Protection and Control, 2015,43(23):1-9.

[11]崔强,王秀丽,王维洲. 考虑风电消纳能力的高载能用户错峰峰谷电价研究[J]. 电网技术,2015,39(4):946-952. CUI Qiang, WANG Xiuli, WANG Weizhou. Stagger peak electricity price for heavy energy-consuming enterprisesconsidering improvement of wind power accommodation[J]. Power System Technology, 2015,39(4):946-952.

[12]何永秀，王冰，熊威，等. 基于模糊综合评价的居民智能用电行为分析与互动机制设计[J]. 电网技术，2012，36(10)：247-252. HE Yongxiu，WANG Bing，XIONG Wei,et al.Analysis of residents’ smart electricity consumption behavior based on fuzzy syntheticevaluation and the design of interactive mechanism[J].Power System Technology, 2012, 36(10)：247-252.

[13]刘辉舟,高飞,胡小建,等.分时电价模型优化方法研究[J]. 电力需求侧管理,2013,15(4):11-14, 23. LIU Huizhou, GAO Fei, HU Xiaojian, et al. The model optimization method of time-of-use price[J]. Power Demand Side Management, 2013,15(4):11-14, 23.

(编辑 刘文莹)

Optimization Model of Residential Time-of-Use Tariff Calculation under Multi-Step Electricity Price

ZHAO Huiru, WANG Yuwei, ZHANG Chao, SHU Yan, ZHAO Mingrui

(School of Economics and Management, North China Electric Power University, Beijing 102206， China)

To design time-of-use (TOU) tariff based on the existing residential multi-step electricity price, and combine the two kinds of prices, which further lead to the rational use of electricity and improve energy efficiency, this paper proposes the optimization model and method of residential TOU tariff calculation under multi-step electricity price. Firstly, according to the user coverage of current each step price, we divide whole residential households into the corresponding sub-group market subdivision. Secondly, we construct the TOU tariff responsive function of every market subdivision, as well as the corresponding optimization objective function set of TOU tariff. Thirdly, we build the constraint condition set of TOU tariff in every market subdivision. Lastly, we construct the TOU tariff optimization model of every segment market with combining the objective function and the constraint condition, whose output result is the optimal TOU tariff for each step. The rationality and feasibility of the model are verified in the example simulation, and the sensitive analysis further reveals the changing law of the optimal TOU tariff results for each step with the demand response.

multi-step electricity price; time-of-use tariff; residential customer; market subdivision; optimization model

国家自然科学基金资助项目(71373076)

TM 714

A

1000-7229(2016)03-0017-07

10.3969/j.issn.1000-7229.2016.03.003

2015-12-06

赵会茹(1963)，女，博士生导师，教授，主要研究方向为电力市场理论与应用技术；

王玉玮(1986)，男，博士研究生，主要研究方向为电力市场理论与应用技术；

张超(1992)，女，硕士研究生，主要研究方向为电力市场理论与应用技术；

舒艳(1991)，女，硕士研究生，主要研究方向为电力市场理论与应用技术；

赵名锐(1992)，男，硕士研究生，主要研究方向为电力市场理论与应用技术。

Project supported by National Natural Science Foundation of China (71373076)