改编高中数学应用问题的探索实践

付晓明

(北京市通州区永乐店中学，北京 101105)

改编高中数学应用问题的探索实践

付晓明

(北京市通州区永乐店中学，北京 101105)

新课程改革力求发展学生的数学应用意识，在教学中要让学生认识到我们学习的数学是有价值的.应用问题承载着让学生体会数学应用价值的使命，因此教师必须加以重视.本文通过对教材中一道例题的分析，做出思考和实践，总结出从实际问题抽象出数学知识的必要性和在此过程中的主要问题，得出选择和编制数学应用问题的原则，并列举了选择和自编数学应用问题的教育实践实例及反思.

数学应用意识 抽象程度 实践

案例：(人教A版高中《数学必修5》第97～98页第3.3.2节例题)某工厂用A、B两种配件生产甲、乙两种产品，每生产一件甲产品使用4个A配件耗时1 h，每生产一件乙产品使用4个B配件耗时2 h，该厂每天最多可从配件厂获得16个A配件和12个B配件，按每天工作8h计算，该厂所有可能的日生产安排是什么？

课本中给出的解答如下：

设甲、乙两种产品分别生产x，y件，由已知条件可得二元一次不等式组

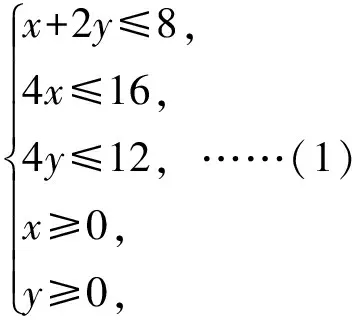
(其余部分省略，详见教科书)

这是为了说明什么是线性规划问题而举的一个例子，为了使例子典型，教科书将实际问题做了抽象，但这个抽象做得并不成功.根据题目的叙述很难得出不等式组(1)，主要有两个原因：(1)题目中并没有“该工厂只能同时加工一种产品”的叙述，因而“x+2y≤8”这个不等式的得出没有依据；(2)题目希望x、y是整数，但在实际生产中完全可以一天生产不完第二天接着生产.例如可行解中的(2，2)，即生产甲、乙两种产品各2件，共用时2+2×2=6小时，余下的2小时只能不工作，这很不符合实际.在教学过程中也有很多学生提出“为什么是小于等于8而不是等于8”这样的疑问.

其实类似的问题在平时很多应用问题中都存在着，这种问题主要是由从实际问题中抽象不到位造成的.题目编制的好坏直接影响着教师应用问题的教学效果以及学生对数学应用价值的理解程度，不可小觑.

一、应用问题的重要作用

《普通高中数学课程标准(实验)》在课程基本理念中提到：“发展学生的数学应用意识.高中数学课程应力求使学生体验数学在解决实际问题中的作用、数学与日常生活及其他学科的联系，促进学生逐步形成和发展数学应用意识，提高实践能力.”[1]可见，我们在教学过程中要让学生真正体会到：数学离我们的生活很近，能够帮助我们解决身边的实际问题，是有价值的数学.只要教师有所重视，并在教学中不断渗透，学生就会不断提高应用意识.

而要想让学生实现自主探究、动手实践、解决实际问题，并不是一蹴而就的，要在前期做大量的铺垫和准备.通过教育实践，笔者总结出发展学生的数学应用能力，大概要经历这样几个层次：(1)通过解决给出的实际应用问题，初步体会数学的应用价值，提高学习数学的兴趣；(2)积累数学的基本知识、基本技能、基本思想和基本活动经验，提高应用数学解决问题的能力；(3)从生活中提出问题，建立数学模型，解决实际问题.不同的学生由于能力的不同，思维方式的差异，能达到的水平会有所不同，难度可以区分，但是过程必须经历.

在第一个层次中，应用问题承载着让学生体会数学应用价值的使命，也是学生最容易接受的形式，我们必须重视这个环节，多思考，选择或编制能够反映数学应用价值的应用问题.

二、从实际问题抽象出数学应用题的必要性

要提高学生的数学应用能力，必须循序渐进，如果直接让学生从生活中提出问题，建立数学模型，再来解决实际问题是不现实的，所以就需要给学生一些题目先让他们有所体会.题目从哪里来呢？实际问题往往比较复杂，变量较多，不能直接使用，这就需要做一些提炼才能满足我们希望运用的数学模型.这个过程需要很强的严谨性，稍有疏忽就会出现问题，达不到我们预想的效果.

从实际问题抽象出数学应用问题的过程，如果抽象得不够，就会使学生无从下手，本文所举的案例就属于这种情况.通常，我们将条件加强就可以使问题明确而便于解答.但同时另一个问题又出现了，附加了很多条件，使得问题的应用性变淡，编制的痕迹过重，题目不符合实际，甚至脱离实际.我们在教学中常常关注怎样教会学生，却忽视了应该先对教学做深入思考，才能达到我们所期望的目标.

三、选择和编制数学应用问题的原则

培养和提高学生的数学应用意识，要从提高数学应用问题的教学入手，最该解决的是对题目的选择和编制，让题目尽量贴近生活，符合实际，得出的结果对实际有应用和指导意义.让学生通过解这样的应用问题，体会数学的应用价值，领悟到学习数学的目的是为了解决实际问题.要实现这个目标，教师需要多思考，从生活中积累好的素材，做适当的抽象，成为恰当的数学应用问题.其实教科书在数学应用价值的渗透上已经下了一番功夫了，几乎每一章的最后一节都安排了应用问题，绝大多数题目都很好，只是个别需要进一步推敲，这也给一线教师提出了研究的课题.笔者正是从对大量题目的思考中，加深了问题的理解，并做出了一些实践.

四、选择和自编数学应用问题的探索实践

1.编制应用问题需要留心生活中的问题

例1：某市移动公司开设了两种通信业务：全球通使用者先缴50元基础费，然后每分钟通话费用0.4元，神州行不缴基础费，每分钟通话费用0.6元，若一个月通话x分钟，两种通信业务费用分别为y1，y2；

(1)写出y1，y2与x的关系；

(2)在同一坐标系作出函数图像；

(3)该选择哪种通信业务更划算，为什么？

这个例子是以一次函数为模型的，完全来源于实际生活，几乎没有什么提炼，学生比较容易接受，图像也很直观，学生很好理解，基本没有障碍.

2.编制应用问题需要对实际问题进行抽象

并不是每个题目都这么简单，绝大多数是需要进行抽象的，但抽象要适度，最好有一定的开放性，这样才更符合实际情况，也给学生思考的空间.

例2：某服装批发商批发时尚仔裤，每条仔裤的成本价为40元，批发价60元，为了促销，若批发数量超过100条时，每多批发1条，批发的全部商品的单价就降低0.02元(据调查，他每天批发的货物的最大数量不多于500条)，设批发条数为x条，问题：

(1)设单价为P，求P关于x的函数解析式；

(2)设利润为Q, 求Q关于x的函数解析式；

(3)画出(2)中函数图像并求利润的最大值.

这个例子是有关利润的问题，在解决了以上问题之后，可继续追问：题目中规定了一个情境，就是批发商批发货物的最大数量不多于500条，请思考这个500条制定得是否合理？学生进行讨论，认为合理是对于批发商而言的，也就是批发商所得利润的最大化，其实这个值应是550条，只要不高于这个值，利润都在增加，因此制定是合理的.接着再提问：如果批发商扩大经营，每天批发的货物多于550条，应该如何制订经营策略.学生继续展开热烈讨论.

给学生一定的时间去讨论和分析，他们都可以得出结果，并且通过自我探索的过程，学生从中得到的收获更深刻，也更愿意去分析问题、解决问题，同时还要懂得把课堂放手给学生.现在教科书的每一章内容几乎都设有专门的应用部分，仔细分析会发现，这部分知识并不是突然出现的，从引入开始就有意识地向学生渗透应用的思想，它是贯穿教学始终的隐形线索.如果我们在每一节的教学过程中都有意去渗透，那么最后讲应用问题的时候学生就不会感觉突兀，更不会觉得是在耽误时间了.

数学应用问题的教学，是发展学生数学应用意识的初始阶段，接下来还要在这个基础上进行深入引导和开展教学，我们要将数学的应用意识贯穿在教学始终，指引我们开展教学活动，真正提高学生的数学应用意识，这也是新课程赋予数学教师的任务和使命.希望通过教师的不懈努力让每个学生都有所突破和收获，快乐地学习有价值的数学.

[1]中华人民共和国教育部. 普通高中数学课程标准(实验)[S].北京：人民教育出版社, 2003.

(责任编辑：李 珺)