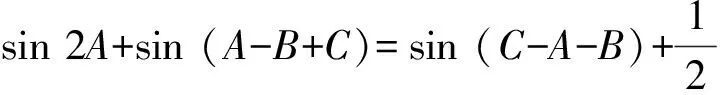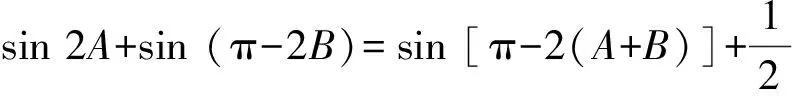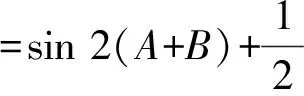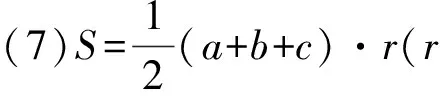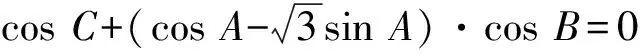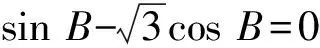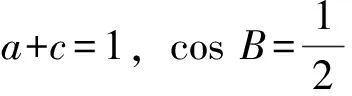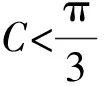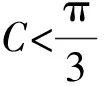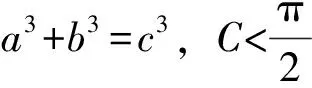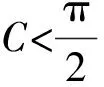正、余弦定理的巧妙应用

韩永权

(山西大学附属中学，太原 030006)

正、余弦定理的巧妙应用

韩永权

(山西大学附属中学，太原 030006)

正、余弦定理揭示了一般三角形中重要的边角关系，它们是解三角形的两个重要定理，是高中数学的重要内容,也是全国各地高考数学中的一个必考知识点．在高考中，解答题、选择题、填空题都考过.常考题型有：(1)根据已知条件求三角形的边或角；(2)三角形面积公式的合理选择；(3)求三角形边、角、周长、面积的取值范围.解决此类问题的关键是正、余弦定理的灵活运用以及对已知条件的合理转化.

正、余弦定理 三角形 应用

题型一 根据已知条件求三角形的边或角

如果题目中已知条件是边、角的混合表达式，通常解题的方法是实现边角的统一，把边化角或把角化边，以实现边、角的互化.

巧妙应用1 边、角互化

例1 (2016课标Ⅰ理)△ABC的内角A,B,C的对边分别为a,b,c,已知2cosC(acosB+bcosA)=c.

(1)求C；

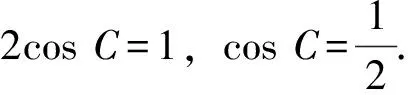
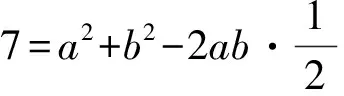
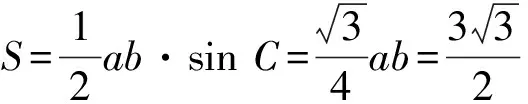
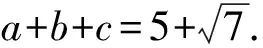
【点评】利用正、余弦定理解三角形，主要是实现边、角的形式统一，把已知条件全部转化成边的关系或全部转化成角的关系.这样可以实现表达式的统一，便于厘清已知条件.本题的实质是射影定理c=acosB+bcosA.在平时的教学中，教师要引导学生多思考、多总结、多积累，只有这样，在遇到不同情境下的问题时，才能做出正确的选择.

巧妙应用2 三角恒等变换

例2 (2016浙江文)在△ABC中，内角A，B，C所对的边分别为a，b，c．已知b+c=2acosB．

(1)证明：A=2B；

解：(1)由正弦定理得，sinB+sinC=2sinAcosB,故2sinAcosB=sinB+sin (A+B)=sinB+sinAcosB+cosAsinB，于是，sinB=sin (A-B)，又A,B∈(0,π),故0

所以B=π-(A-B)或B=A-B，因此A=π(舍去)或A=2B，所以A=2B.

题型二 三角形面积公式的合理选择

三角形的面积公式形式较多，根据已知条件合理选择面积公式，是沟通已知和未知的关键.如下题中，由三角形面积的取值范围，选取相应的三角形面积公式，得出abc的取值范围，进而判断四个选项的正确性.

巧妙应用 选取合适的面积公式

C．6≤abc≤12 D．12≤abc≤24

因为1≤S≤2，所以1≤S3≤8.

【点评】本题中如何合理选择三角形面积公式，是问题解决能力的体现，是沟通已知和未知的桥梁,也是数学能力的体现.三角形的面积公式有下列一些形式：

(4)S=2R2sinAsinBsinC(R为外接圆半径)；

题型三 求三角形中几何元素的取值范围

从高考常见题型出发，从求边、求角、求三角形周长、求面积，即求三角形中几何元素的取值范围进行分类讲解，剖析巧妙应用的方法.解题时主要把三角函数名称、角度统一化归，其本质还是三角函数公式的灵活运用.

巧妙应用1 求三角形边长的取值范围

(1)求角B的大小；

(2)若a+c=1，求b的取值范围．

(2)由余弦定理，有b2=a2+c2-2accosB.

【点评】根据余弦定理可以得出关于b的表达式,再利用基本不等式求出b的取值范围，这是很常规的方法.

巧妙应用2 求三角形角的取值范围

例5 (2012安徽理)设△ABC的内角A,B,C所对的边为a,b,c，则下列命题正确的是______.(写出所有正确命题的序号)

综上可知，①②③正确．

【点评】本题利用函数观点，根据cosC的表达式，利用基本不等式进行放缩，求出角C的取值范围，是一种常规思路.具体步骤是根据已知条件，建立目标函数，求出函数的取值范围，进而确定角的范围.

巧妙应用3 求三角形面积的取值范围

例6 (2014课标Ⅰ理) 已知a,b,c分别为△ABC三个内角A,B,C的对边，a=2，且(2+b)(sinA-sinB)=(c-b)sinC,则△ABC面积的最大值为________.

解：a=2，且(2+b)(sinA-sinB)=(c-b)·sinC，

所以(a+b)(sinA-sinB)=(c-b)sinC，(a+b)(a-b)=(c-b)c，b2+c2-a2=bc．

【点评】一般化和特殊化是数学解题中重要的思维方法，本题中要把2换成a,公式的结构特点呈现出来，解题的思路也就清晰了.

巧妙应用4 求三角形周长的取值范围

(1)求A的大小；

(2)若a=7，求△ABC的周长的取值范围．

解：(1)由正弦定理得，

(2)方法一:由题意，b>0,c>0，b+c>a=7.

【点评】本题的特点是已知三角形的一边和其对角，求三角形周长的取值范围.其实质是求三角形另外两条边的取值范围.一般有两种方法，一种是根据余弦定理，得出其余两边的关系式，即一个二元二次方程，再利用基本不等式得出其余两边的取值范围.另一种是根据正弦定理，转化成角的关系，利用辅助角公式求出三角形其余两边的取值范围.

正、余弦定理是解三角形的两个重要定理.根据题目条件，如果已知两边和其中一边的对角，通常用正弦定理；如果已知两边和夹角，通常用余弦定理.如果已知条件是边角混合表达式，通常把表达式中的边全部转化成角，或把角全部转化成边.三角形中几何元素的取值范围的问题通常用正弦定理结合辅助角公式或余弦定理结合基本不等式解决.正、余弦定理的灵活应用，体现在问题的等价转化上，不仅要求学生熟悉三角公式，而且对运算能力也有较高的要求.不但要会正用正、余弦定理，还要会逆用和变形使用定理.本文从题型、解题方法上对正、余弦定理的灵活运用进行了归类总结，有助于学生从正、余弦定理的巧妙应用上升到解题模式的合理选择.

[1]人民教育出版社课程教材研究所，中学数学课程教材研究开发中心·普通高中课程标准实验教科书数学必修5(A版)[M].北京：人民教育出版社，2007.

[2]刘亚平.课例：“余弦定理”的教学[J].中学数学教学参考(上旬)，2013(7):5-7.

[3]章立丰.课例 ：“解三角形应用举例”(第一课时)[J].中学数学教学参考(上旬)，2015(3):23-25.

[4]郑毓信.数学方法论[M].南宁：广西教育出版社,1996.

(责任编辑：李 佳)