直升机地形辅助导航方法研究
2016-02-23胡水才
胡水才
(海军驻景德镇地区航空军事代表室,江西 景德镇 333000)
直升机地形辅助导航方法研究
胡水才
(海军驻景德镇地区航空军事代表室,江西 景德镇 333000)
为克服直升机在无卫星信号时定位精度不高的缺陷,研究一种适用于直升机上的地形辅助导航方法。在地形辅助导航系统航行规划中,为保证匹配定位精度,必须选择具有较强地形适应性的匹配区域,所以利用两种不同特征的地形进行仿真试验来修正惯导系统指示航迹误差。结果表明,采用等值线匹配算法的地形辅助导航应用在直升机上,是正确的和有效的,可以取得良好效果。
直升机;地形辅助导航;等值线匹配算法
0 引言
惯导系统(Inertial Navigation System,INS)能够全天候提供较全面的导航信息,且具有较强的工作自主性和实时性,具备短期精度高、抗干扰能力强等诸多优点,是直升机航电系统中不可缺少的导航设备之一。但其位置误差随时间积累发散,对于中低等精度INS来说不适合长期使用,必须定期对其进行校正。众所周知,卫星信号容易受建筑物或山体遮挡,特别是在复杂战场环境中,易被敌方无线设备干扰,故而达不到理想精度。因此,仅依靠INS和卫星导航无法满足直升机长期高精度导航的需求。
地形辅助导航系统能很好地解决INS误差积累的问题,近年来受到了广泛重视并已成功使用。地形辅助导航系统中最为关键的技术为匹配算法。目前,较为常用的匹配算法有TERCOM算法、SITAN算法和等值线匹配算法。TERCOM的原理是沿航行路线测量一条地形线,把它与数字地图进行匹配,使实测地形线和从数字地图中提取的基准地形线之间的均方差最小。TERCOM算法对航向偏差较为敏感,并且实时性较差[1-2]。SITAN方法利用INS输出的定位信息,由数字地图导出地形斜率(即地形局部线性化处理),并利用卡尔曼滤波器进行处理。SITAN算法在初始位置误差大和地形起伏剧烈等情况下容易发散[3-4]。等值线匹配算法导航精度很高,其研究逐步走向深入,力求实现快速、稳定、鲁棒性好的匹配算法。因此,对等值线匹配算法展开分析研究具有非常重要的意义[5]。
本文以直升机为研究对象,将地形辅助导航系统分为惯性导航系统、大气数据及高度测量系统、数字地形图和匹配算法四大部分,针对地形辅助导航技术在直升机上应用的特点,研究适用于直升机的地形辅助导航方法。
1 地形辅助导航系统设计方案及算法
1.1 地形辅助导航系统设计方案
地形辅助导航系统设计方案如图1所示。当直升机为执行某项任务飞进某一地形匹配区域后,大气数据系统实时连续地测得直升机的相对气压高度,同时,无线电高度表实时测得直升机的离地高度,将二者的结果做差得到一系列的地形高程点,这些实测的高程点与INS指示的参考位置等信息一起传送到综合显示处理机中;然后,辅助导航系统利用事先存储在综合显示处理机中的数字地图数据与上述传输过来的信息相结合,在匹配算法的作用下,得到相应的极值点,通常认为这些极值点所对应的位置即是直升机的真实位置;最后,利用扩展Kalman滤波算法得到最优的状态估计值,用来补偿INS的积累误差。
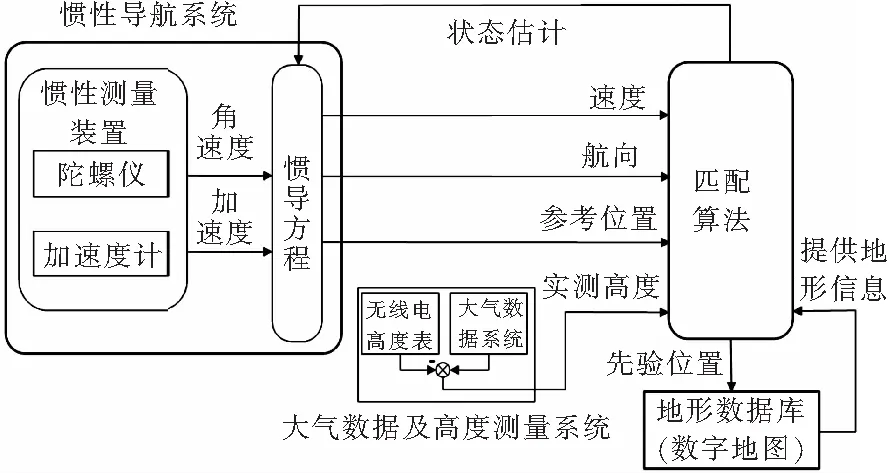
图1 地形辅助导航方案设计
1.2 等值线匹配算法
等值线匹配算法是图像匹配中比较常用的方法之一,它不需事前确定对应估计,只是不断重复运动变换-确定最近点-求运动变换的过程,逐步改进运动的估计。算法的主要思路是:将沿着航迹的高度值连接起来构成曲线,与数字地图中的高度等值线图进行匹配。主要是通过最近点的不断迭代实现测量图像与模型之间的对准匹配。算法采用欧氏距离最小为目标函数,求得测量航迹与真实航迹之间的最优变换,通过该变换校正航迹,实现对惯导测量航迹的校正[6-8]。
如图2所示,直升机进入匹配区后,有一实际航迹,由Ai(i=1,2,…,N)点组成,其中N是估计航迹的长度(点数);同时,惯导系统给出一指示航迹(测量航迹),由点Pi(i=1,2,…,N)组成;另外,Ci(i=1,2,…,N)表示的是当地实测高度等值线,每一条等值线对应于数字地图中的一条等值线。由于惯性导航系统存在积累误差{Pi:(i=1,2,…,N)}和{Ai:(i=1,2,…,N)}之间必定存在误差。等值线匹配算法的思想是Ai必定位于某等值线Ci上,那么可以按照欧氏距离最小准则,使Pi靠近到Ci上,找到最优估计点Yi以及这些点构成的航迹,对惯导系统进行补偿,从而校正惯导系统的积累误差。

图2 等值线匹配算法原理图
等值线匹配算法的原理是:直升机在飞行过程中,惯导系统会给出一系列位置坐标点(xi,yi),并由大气数据系统及高度测量系统获得相应点的高度值hi。对应于每个点寻找它附近高度为hi的等值线上的最近点,并对所测量的路径进行刚性变换(旋转和平移),使集合{Ai:(i=1,2,…,N)}与惯导指示航迹所构成的点集{Pi:(i=1,2,…,N)}距离平方和最小,并重复迭代,直至满足某一要求为止。其具体步骤为:
1) 在匹配区域内测得N个高度数据集合点,记为{Ji:(i=1,2,…,N)};每个高度数据的对应位置在惯导上指示的坐标为(xi,yi),记做Pi;从数字地图中提取高度为{Ji}的等高线,记为Ci;等值线Ci上离Pi距离最小的点记为Yi。
2) 寻找刚性变换T,使集合Y={yi}与集合T{Pi}之间欧氏平方距离最小,即使下式最小:
(1)
式中,T表示变换,包括旋转和平移,上式又可表示为:
(2)
3) 对集合{Pi}应用变换T{Pi},即将新的集合T{Pi}作为起始集合进行下一次迭代,直到收敛或达到收敛次数为止,可应用公式dk-dk+1<α或迭代次数n>N,其中α为满足收敛条件的极值点,即使T停止明显变化的某一值,这需要根据外部具体条件(例如地形特征)而定。
其基本流程图如图3所示。
2 仿真试验
下面对等值线匹配算法进行仿真分析。为验证该算法的有效性和正确性,在MATLAB 7.4.0平台下对基于等值线匹配算法的直升机辅助导航方法进
行仿真分析。
选取2组具有代表性的地形作为仿真用的地形图,其地形等值线图如图4所示。
地形A和地形B的网格大小均为41×36,分辨率为30m×30m,其地形参数统计表见表1。
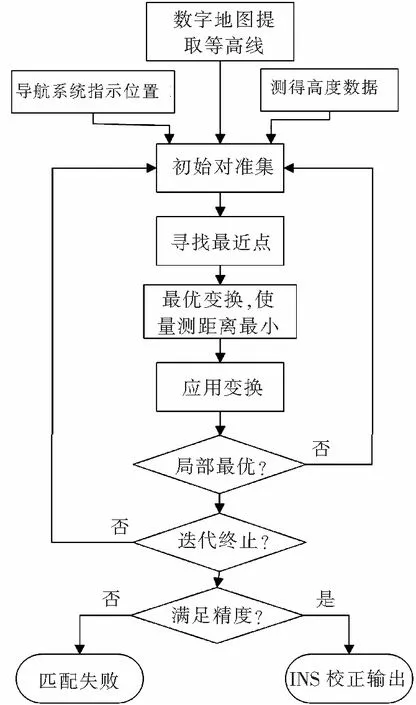
图3 等值线匹配算法流程图
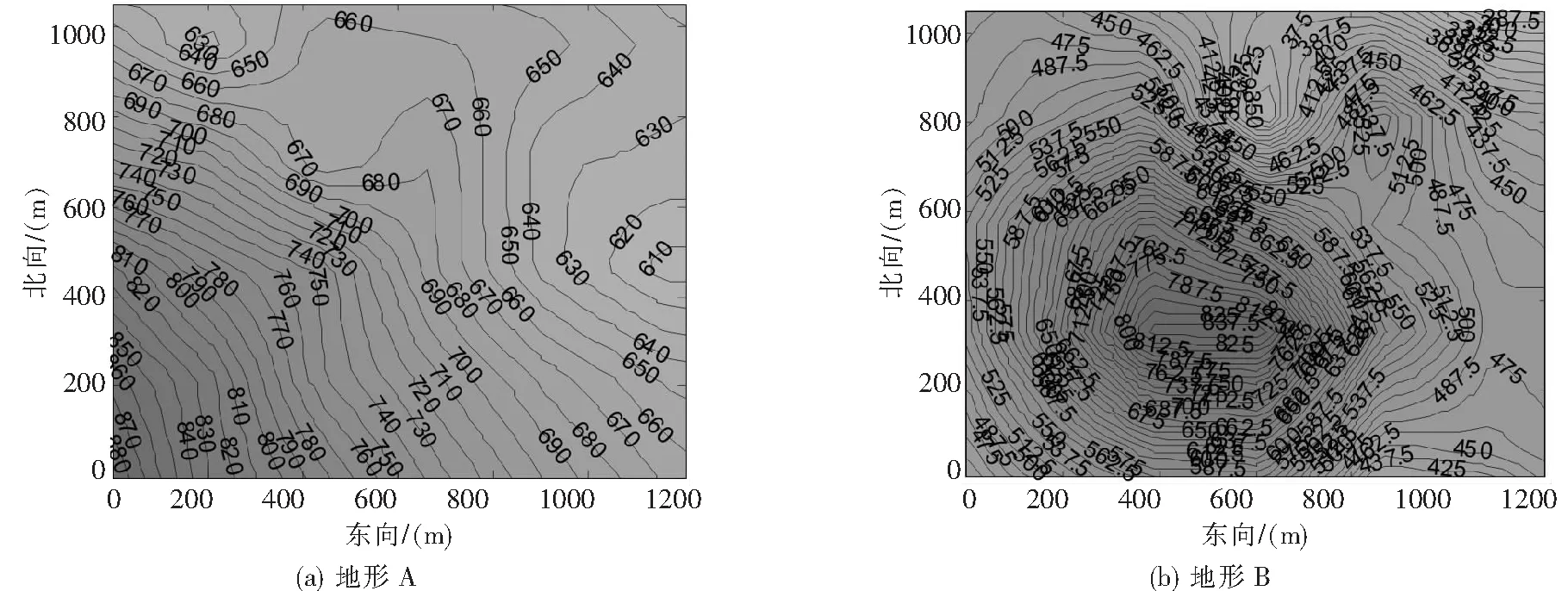
图4 地形A和地形B等值线上色图

地形最大值/(m)最小值/(m)平均值/(m)高程熵高程差异熵高程标准差/(m)地形A890.3389606.9602697.99050.999320.9990065.0767地形B849.7773274.3638540.62820.999290.99895120.8009
高程差异熵用来描述地形相对差异程度,高程熵用来评价地形信息量的丰富程度(该值越小,地形复杂程度越高),而高程标准差用来描述地形偏离平均水平的程度(该值越大,偏离平均水平的程度越大)。从表1中可以看出,地形A的高程熵和高程差异熵比地形B的要小,而高程标准差比地形B的要大,说明地形A比地形B的地形信息量更为丰富且更不平坦。
图5(a)和图5 (b)表示最后一次迭代并进行旋转和平移变换之后的匹配航迹和匹配精度情况。从图5中可以很明显地看出,等值线匹配算法构成的曲线经过几次迭代之后,就会逐渐逼近实际航迹,并具有较好的定位精度。
图6(a)和图6 (b)表示出在地形特征比较明显的地区进行地形匹配,等值线匹配算法会得到更好的匹配效果,匹配航迹更接近于实际航迹。
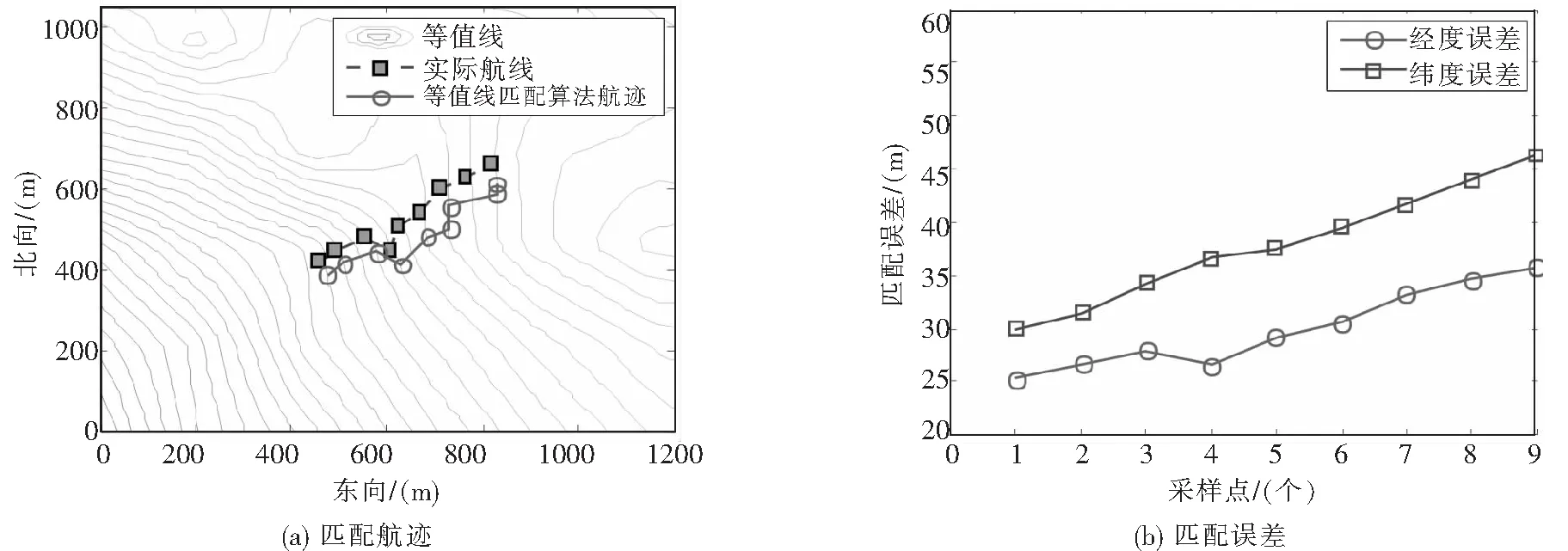
图5 地形B中,匹配航迹及匹配误差
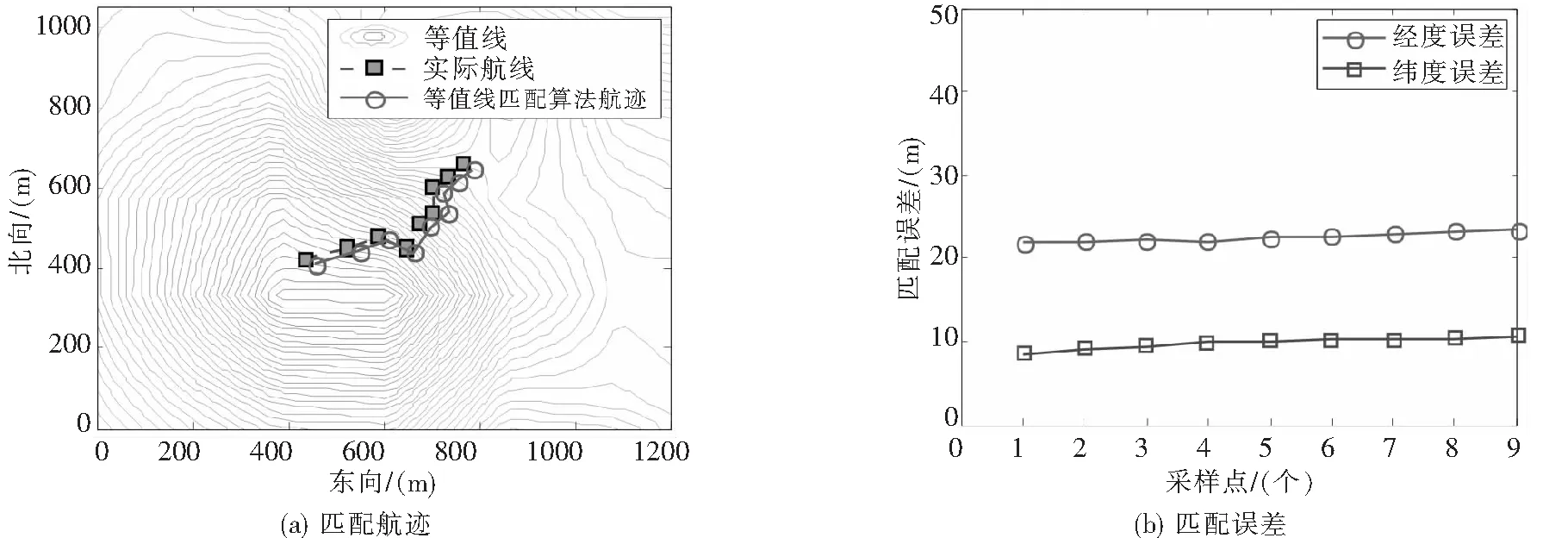
图6 地形A中,匹配航迹及匹配误差
3 结论
采用等值线匹配算法作为直升机地形辅助系统中数据处理的主要方法,主要优点是它不需要对数字地图的数据做预处理且算法的原理简单。仿真试验表明了该算法的正确性和有效性,在不同的地形下,都能得到良好的效果。但此次仿真试验的前提是在不超出数字地图的情况下,若该算法初值点取在数字地图边缘,就可能出现野值点的问题,并且考虑到直升机在实际航行中的隐蔽性及发起突然袭击等问题,需要很好地进行路径规划,这些都有待进一步的研究。
[1] Yan L, Cui C F, Wu H L. A gravity matching algorithm based on TERCOM[J]. GeomInfSci Wuhan Univ,2009(34):261-264.
[2] 李雄伟,刘建业,康国华. TERCOM 地形高程辅助导航系统发展及应用研究[J]. 中国惯性技术学报,2006,14(1):34-40.
[3] Chen H H, Ji M. Comparison of methods for expanding the convergence region of SITAN system[C]. IEEE Proceedings of the National Aerospace and Electronics Conference, 1986: 288-292.
[4] Creel E E. Data compression techniques for use with the SITAN algorithm[C]. IEEE PLANS, Position Location and Navigation Symposium, 1986: 309-315.
[5] Yang Y, Wang K D. Mismatching judgment using PDAF in ICCP algorithm[C]// Fourth International Conference on Natural Computation, Piscataway: Inst. of Elec. and Elec. Eng. Computer Society, 2008: 172-176.
[6] 童余德,边少锋. 实时等值线算法重力匹配仿真[J]. 中国惯性技术学报,2011,19(3):340-343.
[7] 李姗姗,吴晓平. 水下重力异常最近等值线迭代匹配算法的改进[J]. 武汉大学学报(信息科学版),2011,36(2):226-230.
[8] Jiang F, Wu Y M, Zhang Z S, et al. Combinational seabed terrain matching algorithm basing on probability data associate filtering and iterative closest contour point [C]// 2009 Second International Conference on Intelligent Computation Technology and Automation, Piscataway: IEEE Computer Society, 2009: 245-249.
Research on Helicopter Terrainaided Navigation Method
HU Shuicai
(Navy Aviatic Representative Office in Jingdezhen, Jingdezhen 333000, China)
In order to overcome the defect that positioning accuracy is not high under condition of Satellite signal invalidation, terrainaided navigation method was studied to apply helicopter. To ensure precision of matching guidance, the regions which have good adaptabilities should be chosen. And by known reserved terrain data, the accumulative errors of the inertial navigation could be corrected. The simulation results showed that contour matching algorithm on helicopter terrain navigation was correct and effective. Good effects could be obtained.
helicopter; terrainaided navigation; contour matching algorithm
2015-10-08 作者简介:胡水才(1976-),男,江西乐平人,本科,工程师,主要研究方向:直升机质量控制。
1673-1220(2016)01-024-04
V249.3
A
