参数驱动骨架模型在直升机旋翼仿真中的应用
2016-02-23彭利乐方永红金坤健
彭利乐,方永红,金坤健
(中国直升机设计研究所,江西 景德镇 333001)
参数驱动骨架模型在直升机旋翼仿真中的应用
彭利乐,方永红,金坤健
(中国直升机设计研究所,江西 景德镇 333001)
简要介绍了“骨架模型(Skeleton)”和“参数化驱动”的概念。通过一个实例,较详细地阐述了骨架模型的建模方法及其在旋翼运动学仿真中的应用。同时也简要介绍了通过CATIA编程实现仿真模型参数的自动化遍历。
骨架模型;直升机;旋翼系统;仿真
0 引言
所谓“参数驱动骨架模型(Skeleton)”,是一个根据产品构型参数而定义的受约束的几何元素(点、线、面)的集合,该集合中的几何元素的几何要素(长度,空间位置,相互关系等)与一个构型参数集相关联,通过修改参数可实现模型的自动更新。
自20世纪70年代开始,随着信息技术的发展,发达国家在诸如航空航天、超大规模集成电路等复杂系统行业逐渐引入“自顶向下(Top-Down)”这一设计理念及方法,在项目概念设计阶段,按系统工程的思想进行自顶向下的设计,先定义系统整体需求、功能、约束,再根据系统内部因素的耦合度进行子系统或模块划分,并定义子系统的要求、功能及约束[1]。由此人们对这一理念的灵魂——“骨架”的认识也越来越深入,在产品的打样设计阶段,根据设计目标而初步确定的总体参数用骨架的方式来定义,人们在这一图形化了的总体参数表上进行零部件的设计,这样在设计的每个阶段毋须进行零部件的装配即能实时地看到最终产品的概貌,从而在第一时间发现问题,调整参数。由于事先已将参数集与骨架模型进行了关联,因此随着各项参数的更新,骨架模型也将自动进行更新,实现了真正意义上的“参数驱动”。
本文通过一个应用实例,结合CATIA平台,较详细地阐述骨架模型的建立,参数与骨架的关联方法以及该骨架模型在旋翼运动学仿真中的应用。
1 问题的提出
1.1 背景知识
旋翼系统是直升机最为重要的系统之一,为直升机提供主要的升力和操纵力。旋翼桨毂系统除了具有传递来自桨叶的载荷的功能外,还必须提供桨叶沿变距、挥舞和摆振三个方向的运动[2]。对于桨毂系统而言,每个飞行状态的运动谱不同,相同飞行状态下每个挥舞支臂在同一时刻的三个方向的运动相位角也均不同,因此桨毂系统运动极为复杂。如何在旋翼方案设计阶段,根据桨叶的运动谱来获得桨毂各运动副成品的运动谱,为轴承类成品的设计输入及试验验证提供依据就显得尤为重要。如果想通过解析的方法,其过程极为复杂,且数据量很大;通过参数化骨架模型的运动仿真,借助后台程序驱动,则问题变得相对简单而清晰,达到事半功倍的效果。本文通过某型机桨毂阻尼器杆端轴承的运动谱的求解,来简单介绍参数驱动骨架模型在旋翼运动学仿真中的应用。
1.2 挥舞支臂的三种运动
旋翼系统作为直升机的主要动部件,其运动除绕旋翼轴的转动外,每个挥舞支臂还存在以下三个方向的运动(见图1):
1) 变距运动θ:绕变距轴线的转动;
2) 挥舞运动β:绕挥舞铰的转动;
3) 摆振运动δ:绕摆振铰的转动。

图1 挥舞支臂的三种运动
1.3 阻尼器杆端轴承的三种运动
阻尼器分别通过其两端的杆端的关节轴承与两个挥舞支臂相连,随着相邻的两个挥舞支臂的运动(θ、β和δ),杆端轴承的外圈相对其内圈也同样存在三个方向的运动: 弯曲运动β′,弯曲运动θ′,扭转运动δ′(见图2)。
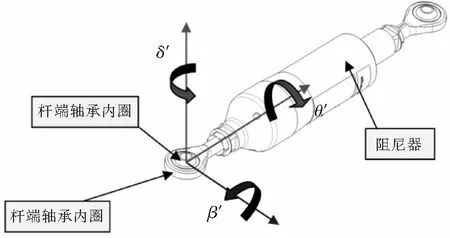
图2 阻尼器杆端轴承的三种运动
1.4 旋翼系统运动谱计算分析
在旋翼系统设计过程中,必须对旋翼系统的运动规律进行分析计算,分析所得的结果构成桨毂系统弹性元件(弹性轴承、阻尼器等)和阻尼器杆端轴承的设计输入以及进行结构干涉性检查的依据。
运动谱计算分析可分为两部分内容:
1) 挥舞支臂的运动谱计算
该部分的计算通过商业软件CAMRADⅡ完成,输出结果为旋翼系统每个支臂在其绕旋翼轴旋转一周时三个方向运动的运动方程,即:
θ1=θ0+θCCOS(ωt)+θSSIN(ωt)
β1=β0+βCCOS(ωt)+βSSIN(ωt)
δ1=δ0+δCCOS(ωt)+ δSSIN(ωt)
与之相邻的另一支臂的运动方程则为:
θ2=θ0+θCCOS(ωt+φ)+θSSIN(ωt+φ)
β2=β0+βCCOS(ωt+φ)+βSSIN(ωt+φ)
δ2=δ0+δCCOS(ωt+φ)+δSSIN(ωt+φ)
其中:θ0、β0、δ0—静态量;θC、βC、δC—余弦分量;θS、βS、δS—正弦分量;ωt—相位;φ—两支臂间的夹角。
将上面单一支臂的三个方程绘成图表如图3所示,从图中可以看出,三个方向的运动周期相同,但幅值和初始相位均不同。
2) 阻尼器杆端轴承的运动谱计算
既然已知相邻两个挥舞支臂的运动规律,如何根据这种规律来求解出阻尼器杆端轴承的运动谱以满足杆端轴承设计依据及疲劳试验的加载需要则是本文讨论的主要内容。由于挥舞支臂的运动与杆端轴承的运动不存在简单的函数关系,因此如果采用传统的解析计算的方法来求解,势必造成数据量巨大且极易出错,因此在以往,这部分的分析通常采用经验类比的方法进行,所得结果不尽如人意。
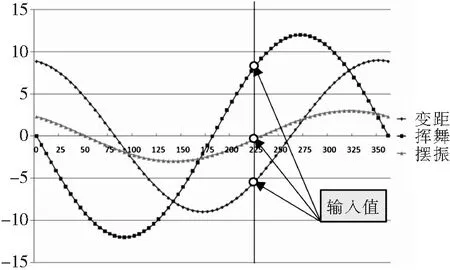
图3 挥舞支臂典型运动曲线
采用参数驱动骨架模型则能轻松解决这一难题。
2 模型的建立[3]
须说明的是,本文所讨论的模型是在CATIA V5环境下建立。
2.1 定义参数
首先在CATIA环境下定义骨架模型所使用的所有参数,这些参数分为三类:
1) 构型参数——考虑到模型的通用性,在建立旋翼系统骨架时将旋翼(主要是桨毂)的所有构型参数定义出来并输出成一个构型设计表(格式为EXCEL,具体方法参见CATIA帮助文档),以后在进行不同型号的旋翼系统仿真时只需在构型设计表中增加一行参数,一行参数对应一种构型。
2) 输入参数——即两个相邻挥舞支臂的6个运动参数,这些参数也须输出成另一个设计表,接下来我们将通过选择设计表中的不同配置(Configuration)来完成参数的输入(具体原理请参见CATIA帮助文件)。
3) 输出参数——即两个杆端关节轴承的6个运动参数。
2.2 建立模型
1) 模型构建流程
挥舞支臂1:旋翼轴(直线)→挥舞铰外伸量平面(平面)→挥舞支臂所在竖直平面(平面)→摆振铰(直线)→挥舞铰(直线)→通过挥舞铰且垂直支臂的平面(平面)→挥舞运动后的摆振铰(直线)→带挥舞运动且垂直于支臂的平面(平面)→弹性轴承球心(点)→挥舞支臂(直线)→通过阻尼器连接节点且垂直于支臂的平面(平面)→通过支臂的竖直平面(平面)→通过支臂且存在变距角的平面(平面)→通过阻尼器连接节点且存在变距角的平面(平面)→阻尼器杆端轴承内圈上下对称面(平面)→阻尼器连接节点(点)。
挥舞支臂2:按支臂1相似的流程构建模型,唯一不同之处在于阻尼器连接点相对于挥舞支臂的前后缘方位不同和存在沿垂直方向的高度差。
阻尼器及杆端:两个阻尼器连接节点的连线(直线)。
最终完成的骨架模型见图4。

图4 骨架模型
2) 构建模型时的规律
从上节所述流程可以看出,我们在构建模型时必须遵循从主动端至从动端的顺序,即明确“谁驱动谁”的问题。在本例中不难看出是两个相邻的挥舞支臂在“驱动”阻尼器及其杆端轴承。
如果说运动机构的连接与驱动靠的是运动副的话,那骨架模型各几何元素(点、线、面)间则依赖约束来驱动;
另外,在构建模型时,我们应尽量避免通过直接输入坐标的方式来约束几何元素,而应通过偏移、旋转、相交等构造方式来定义,这样就能在建模的过程中施加约束。
2.3 参数与模型的关联
既然是“参数驱动”的骨架模型,那参数与模型之间如何关联呢?其实非常简单,在我们构建模型的过程中需要添加很多约束。通常我们在添加约束时输入的是特定的数值,在此则不同,输入的是函数,而函数的自变量则是在2.1节中定义的各个参数,这样当我们在设计表中改变参数值时骨架则能自动更新。
3 实例分析
3.1 输入参数(设计表)的准备
根据载荷部门提供的挥舞支臂的运动方程(见§1.4),我们将相位ωt每隔5°(考虑到效率和精度的折衷)计算一个点,每个点得出两个支臂共6个角度值作为骨架模型的输入参数。所有飞行状态所有计算点的输入值构成了§2.1节定义好的输入设计表中的内容(见图5)。

图5 输入设计表
3.2 求解与结果的输出
通过选择设计表中的不同构型(Configuration)来向骨架输入六个参数,即旋翼系统在某一方位两个挥舞支臂的变距角、挥舞角和摆振角(见图2),更新骨架(其实就是一个求解的过程),利用CATIA的测量功能就能直接测量出求解所需的杆端轴承的六个角度,并将测量结果赋值给§2.1节中定义的六个输出参数,这样我们就完成了单一方位的计算(图6)。

图6 输出结果
4 求解过程的自动化
通过前面的叙述,我们已经清楚了构建参数驱动的骨架模型并利用该模型进行运动参数求解的方法。然而对直升机而言,其飞行谱包括了几十种飞行状态(悬停、滑跑、俯冲拉起等等),而对每一个飞行状态旋翼的运动规律都不同,也就是一个飞行状态对应一个图3中的3条曲线,并且对一个飞行状态而言,要完成旋翼在旋转一周的过程中阻尼器杆端的运动谱,就算每隔5°求解一次也须完成72个“选择设计表中的一行参数(Configuration)→更新骨架→记录结果”的循环,显然,要想得到整个飞行谱中各个状态下的杆端轴承的运动谱就不得不完成几千次这样的循环,手动处理不可行,通过编程让程序来完成自动化处理显得尤为重要。
CATIA“知识工程”模块中提供的VBA编程环境使这一切迎刃而解[4]。
自动处理程序逻辑框图见图7。
通过运行该程序,能自动完成整个的求解过程,并且在运行过程中能对输入输出参数和整个骨架模型实现动态显示,对输出结果能格式化后写入磁盘文件。
该程序已在CATIA V5R16环境下调试通过。
5 其它应用
除上述求解杆端轴承的运动谱外,本模型通过增加相关输出可实现以下所述其它功能:
1) 计算阻尼器的运动谱;
2) 优化设计阻尼器前后缘高度差;
3) 通过将实体固接在骨架上的方法完成旋翼桨毂系统的干涉性检查等。

图7 程序逻辑流程图
6 结论
通过参数驱动骨架模型在旋翼运动学仿真中的应用,为旋翼尤其是桨毂系统的结构设计提供了依据,在构型参数的优化、成品件(如阻尼器杆端轴承)技术要求的确定和结构的干涉性检查等方面提供了更为精确而高效的分析方法。
本方法已成功应用于多型直升机旋翼系统总体参数的优化。
[1] 罗婷婷,杨伟俊.基于骨架模型的航空发动机自顶向下设计方法研究[J].数字军工,2013(5):26-30.
[2] 张呈林,张晓谷,郭士龙.直升机部件设计[Z].航空专业教材审查组,1986.
[3] Dassault Co.CATIA V5R16 online document[Z].2006.
[4] Dassault Co.CAA V5 Visual Basic help[Z].
Application on Helicopter Rotor System Emulation for Parameter Drive Skeleton
PENG Lile, FANG Yonghong, JIN Kunjian
(China Helicopter Research and Development Institute, Jingdezhen 333001, China)
This article briefly introduced the concepts of “skeleton” and “parameter drive”. The skeleton modeling method and its application on rotor system motion emulation were described in detail. The parameters automatic ransack method by CATIA program was also briefly introduced in this article.
skeleton;helicopter ;rotor system;emulation
2015-11-20 作者简介:彭利乐(1970-),男,江西湖口人,大学,高工,主要研究方向:直升机旋翼系统设计。
1673-1220(2016)02-006-05
V222; V221+.92
A
