基于圆轨迹与外摆线轨迹的直升机双线摆吸振性能对比分析

黄国科，郭俊贤 ， 赵 军

(中国直升机设计研究所 旋翼研究室，江西 景德镇 333001)

基于圆轨迹与外摆线轨迹的直升机双线摆吸振性能对比分析

黄国科，郭俊贤 ， 赵 军

(中国直升机设计研究所 旋翼研究室，江西 景德镇 333001)

基于拉格朗日方法，建立圆轨迹和外摆线轨迹的双线摆/旋翼/机身耦合系统的非线性动力学方程组；通过数值仿真，更深入系统地研究双线摆设计参数对圆轨迹和外摆线轨迹双线摆吸振性能的影响的规律，并进行对比分析。研究表明，外摆线轨迹模型综合吸振性能优于圆轨迹模型。

直升机；双线摆；吸振性能；动力学

0 引言

在直升机的发展中，旋翼桨毂双线摆式吸振器[1-2]是一种应用较广泛的被动离心摆式动力吸振器，对振源直接吸振，吸收旋翼(N±1)Ω水平激振力，能降低桨毂旋转面内的振动载荷，从而降低机身的振动水平。双线摆式吸振器装在桨毂上，只需改动桨毂部分零件，不需对机体结构进行大的修改，因而设计改动量小，易于设计，且能随旋翼转速而调谐，对不同旋翼转速都有效。鉴于其在减振方面的优点和有效性，对双线摆的研究具有重要的工程实用价值和理论意义。

但至今，国外对直升机双线摆式吸振器减振的有效性和型号应用报导较多，对其研究的理论文献公开发表很少。Miao W和Mouzakis T用模态迭加法建立机身/旋翼/双线摆式吸振器耦合系统的动力学方程，仅初步讨论了吸振器设计参数对其减振性能的影响； Olivier A和Bauchau J R[3]从多体动力学角度对双线摆运动作了细致分析，但不讨论参数以及不同轨迹对吸振器减振效果的影响规律。国内,南京航空航天大学顾仲权[4]等人用阻抗分析方法研究了桨毂上装有4支臂双线摆减振器的动力学，仅对圆轨迹双线摆结构设计参数作了相应分析，未考虑外摆线轨迹。西北工业大学杨茂[5]等曾针对“黑鹰”的双线摆减振器的动力学和减振有效性进行过分析，但对耦合系统建模与不同轨迹分析等问题缺乏深入的研究。

本文建立圆轨迹和外摆线的双线摆/旋翼/机身耦合系统的非线性动力学方程组；深入研究摆锤质量块、加速度阻抗、阻尼比、频率调谐、激振力对不同轨迹双线摆吸振性能的影响的规律，并进行对比分析，更进一步揭示不同轨迹吸振性能的不同特性。

1 动力学建模

1.1 分析模型

双线摆吸振器物理简化模型如图1 所示。吸振器可简化为长度为R的支臂以转速Ω绕旋转中心O点旋转，支臂边缘铰接一摆长为r，摆锤质量为m的单摆，且该单摆始终在支臂的旋转平面内作摆动。

图1 双线摆吸振器物理简化模型

双线摆/旋翼/机身耦合动力学分析模型及坐标系如图2所示。桨毂旋转坐标系xhyhzh相对不旋转坐标系XHYHZH在激振力和激振力矩作用下的偏移量分别为x,y和θz。假定双线摆具有N个支臂，第i个支臂上的摆锤质量块质量为mi，有效支臂长度Ri，对应方位角为φi，有效摆长为ri，相对支臂的摆角为φi。

1.2 动力学方程

对于由N片桨叶和N个双线摆式吸振器及机身、旋翼组成的非保守系统，拉格朗日方程可表述为：

(1)

其中T为动能,U为势能，D为耗散函数，广义坐标q=(xi，yi，φi)T。

图2 双线摆式吸振器的耦合分析模型及坐标示意图

圆轨迹与外摆线轨迹对比如图3所示。

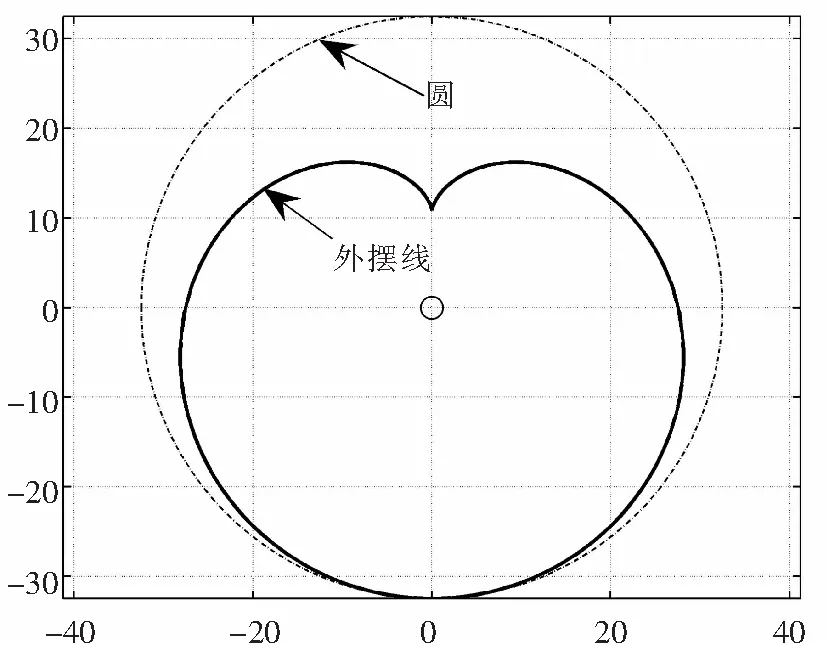
图3 圆轨迹与外摆线轨迹对比

根据坐标变换关系，对于圆轨迹模型，第i个双线摆动质量质心在惯性坐标系下XHYHZH的坐标表示为：

(2)

(3)

根据外摆线轨迹的几何定义[6]，得到有效摆长表达式为：

(4)

根据坐标变换关系，外摆线轨迹双线摆第i个双线摆动质量质心在惯性坐标系下XHYHZH的坐标表示为：

(5)

(6)

将各表达式代入拉格朗日方程，可分别建立圆轨迹与外摆线轨迹的双线摆/旋翼/机身耦合系统动力学方程，写成矩阵微分方程形式如下：

(7)

式中，M为质量矩阵，C为阻尼矩阵，K为刚度矩阵，F为激振力矩阵。

将动力学方程组化为一阶常微分动力学方程组。采用在工程上广泛应用的Runge-Kutta法进行求解。处理过程如下：

通过转换可得：

(8)

作变量变换：

则原方程可化为一阶常微分方程组：

(9)

2 吸振性能对比仿真分析

定义旋翼旋转平面内作用于桨毂中心处x、y向的外部激振力幅值分别为Fx，Fy。外部激振力分别为：fx=Fxcos(NΩt)，fy=Fysin(NΩt)，桨毂残余力幅值分别为Frx,Fry。如果|Frx|<|Fx|且|Fry|<|Fy|，则吸振器有效，否则，吸振器无效。当|Frx|<|Fx|且|Fry|<|Fy|时，|Frx|<|Fx|和|Fry|<|Fy|的大小作为评价吸振器减振效率的指标，比值越小，减振效率越高。

本小节主要考虑双线摆某个参数单一变化，而其他参数固定不变的情况下，研究摆锤质量块、加速度阻抗、阻尼比、频率调谐、激振力等双线摆参数对圆轨迹和外摆线轨迹双线摆吸振性能的影响规律，并进行对比，进一步分析不同轨迹吸振性能的优劣。假设x、y向的加速度阻抗、激振力幅值相等，数值仿真的主要双线摆设计参数如表1。

表1 双线摆吸振器参数

2.1 摆锤质量块影响分析

对于圆轨迹路径模型和外摆线路径模型，分别计算质量块质量m从0kg到30kg变化时，桨毂残余激振力和摆角的变化情况(见图4)。

图4 圆轨迹与外摆线路径模型桨毂残余力和摆角随质量的变化情况

从仿真结果分析发现：

1)质量跳跃点不同。圆轨迹吸振性能在m=8.7kg时发生跳跃，而外摆线吸振性能在m=1kg时发生跳跃，即外摆线质量块质量有效吸振范围远远大于圆轨迹。

2)在减振失效区域，两种双线摆都成为激振器，摆角都处于大摆角范围内。但是圆轨迹桨毂残余力最高值达到300%，远远大于外摆线最大值112.4%，此时圆轨迹路径模型成为严重的振动源。

3)在减振有效区域，两种路径的减振效果都能随着质量的增大而增加。但是圆轨迹路径的残余力能达到3%，远小于外摆线的15%,因此圆轨迹模型减振效果要高于外摆线模型。

2.2 加速度阻抗影响分析

对于圆轨迹路径模型和外摆线路径模型，分别计算加速度阻抗从0kg到2000kg变化时，桨毂残余激振力和摆角的变化情况(见图5)。

从图5的仿真结果分析：

1)对于圆轨迹路径模型，当加速度阻抗增大到245kg时，存在跳跃点，即此时质量块质量10kg是阻抗为245kg时的质量跳跃点

2) 对于圆轨迹和外摆线轨迹,随着加速度阻抗的持续增加，桨毂残余激振力随之趋近于100%，摆角随之趋近于0度，不过圆轨迹摆角趋近于0的速度要慢于外摆线轨迹。

3)随着加速度阻抗的变化，圆轨迹从吸振器变为激振器，外摆线模型一直处于减振有效区域，不会成为激振器，优于圆轨迹模型。

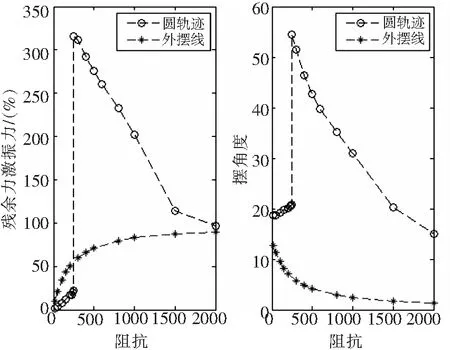
图5 圆轨迹与外摆线模型桨毂残余力和摆角随加速度阻抗变化情况

2.3 阻尼比影响分析

对于圆轨迹路径模型和外摆线路径模型，分别计算阻尼比从0.01到0.2变化时，桨毂残余激振力和摆角的变化情况(见图6)。

从图6的仿真结果分析：

1)对于圆轨迹和外摆线路径模型，随着阻尼比的增加，桨毂残余激振力都随之增加，质量块摆角幅值都随之降低。

2)在阻尼比增加到一定程度后，圆轨迹残余激振力大于外摆线，即此时外摆线路径模型的减振效果要高于圆轨迹模型。

图6 圆轨迹与外摆线模型桨毂残余力和摆角随阻尼比的变化情况

3)外摆线路径模型受阻尼比影响较小，即对双线摆各部件的表面质量、磨损等精度要求比圆轨迹路径模型低。

2.4 调谐影响分析

对于外摆线路径模型，分别计算双线摆固有频率从2.4Ω到4.8Ω变化时，桨毂残余激振力与质量块摆角幅值的变化情况(见图7)。

从图7仿真结果分析：

1)圆轨迹与外摆线桨毂残余力和摆角随频率的变化规律的趋势基本一致。

2)振动峰值频率与反共振点的不同，外摆线轨迹要比圆轨迹前移约0.4Ω。

对于4Ω的激振力，外摆线模型处于过调状态，而圆轨迹模型正好处于共振调谐状态。这也解释了一般情况下，圆轨迹模型吸振能力要高于外摆线模型。而随着摆角的增大，由于刚度软化，双线摆固有频率会进一步降低，圆轨迹模型处于欠调状态，而外摆线模型仍处于过调状态或者接近调谐共振，因此在大摆角非线性状态，圆轨迹模型容易进入减振无效区域，而外摆线模型仍能有效激振。因此从频率调谐的角度来看，外摆线模型优于圆轨迹模型，有比较大的减振有效裕度。

图7 圆轨迹与外摆线桨毂残余力和摆角随频率调谐的变化对比情况

2.5 激振力影响分析

对于圆轨迹路径模型和外摆线路径模型，分别计算激振力F从1000N到9000N变化时，桨毂残余激振力和摆角的变化情况(见图8 )。

从图8仿真结果可以看出，在减振有效范围内，圆轨迹路径模型的减振效果要高于外摆线模型。但当激振力增大到5900N时，圆轨迹模型残余力幅值出现跳跃，从吸振器变为激振器。而外摆线模型在激振力增大到9000N时，仍处于减振有效区域。这主要是当激振力增大时，摆角幅值也相应增大，由于刚度软化导致固有频率的下降，且圆轨迹模型的共振调谐点要大于外摆线模型，因此圆轨迹模型相对于外摆线模型，提前进入欠调状态，导致振动过大，从吸振器变为激振器。综上分析，外摆线模型可以工作在更大的激振力范围，优于圆轨迹路径模型。

图8 圆轨迹与外摆线路径模型桨毂残余力和摆角随激振力变化对比情况

3 结论

通过数值分析，圆轨迹和外摆线轨迹双线摆吸振性能影响规律对比分析的结论如下：

1)外摆线路径模型质量块质量有效吸振范围远远大于圆轨迹，有利于双线摆根据试验、试飞振动情况进行质量块质量的调整选择。

2)在减振失效区域，圆轨迹的桨毂残余力最高值达到300%，远远大于外摆线的最大值112.4%，此时相对于外摆线，圆轨迹路径模型成为更严重的振动源。

3)在减振有效区域，圆轨迹模型减振效果要高于外摆线模型。

4)随着加速度阻抗的变化，外摆线模型一直处于减振有效区域，不会成为激振器，优于圆轨迹模型。

5)外摆线路径模型受阻尼比影响较小，即对双线摆各部件的表面质量、磨损等精度要求比圆轨迹路径模型低。

6)由于振动峰值频率与反共振点的不同，外摆线轨迹要比圆轨迹前移约0.4Ω。因此从频率调谐的角度来看，外摆线模型优于圆轨迹模型，有比较大的减振有效裕度。

7)由于刚度软化导致固有频率的下降，圆轨迹提前进入欠调状态，在激振力不大时吸振器变为激振器。因此外摆线模型可以工作在更大的激振力范围，优于圆轨迹路径模型。

[1] Miao W, Mouzakis T. Bifilar Analysis Study (Volume I) [R]. NASA CR 159227, 1980.

[2] 赵 军，黄文俊，黄 珺.直升机旋翼双线摆式吸振器的关键技术[J].航空科学技术，2012(4)：50-53.

[3] Olivier A, Bauchau J R, Chen S Y. Modeling the Bifilar Pendulum Using Nonlinear, Flexible Multi-body Dynamics [J]. Journal of the American Helicopter Society, 2003, 48(1):53-62.

[4] 王鸿斌，顾仲权.直升机双线摆式吸振器的动特性研究 [J].南京航空航天大学学报，2004, 36(4):427-432.

[5] Yang M, Chopra I, Haas D J. Vibration Prediction for Rotor System With Faults Using Coupled Rotor-Fuselage Model [J]. Journal of Aircraft, 2004, 41(2):348-358.

[6] 刘小磊.基于多体动力学的直升机双线摆桨毂吸振器研究[D].南京：南京航空航天大学航空宇航学院，2012.

The Comparing Investigation of Bifilar Pendulum Vibration Absorption Performance about Circle Path and Epicycloid Path

HUANG Guoke, GUO Junxian, ZHAO Jun

(China Helicopter Research and Development Institute, Jingdezhen 333001, China)

In this paper, a coupled nonlinear dynamical formulation for bifilar pendulum/rotor/ fuselage about different paths was developed based on Lagrange Principle. The comparing effects of bifilar pendulum design parameters about circle paths and epicycloid path on the vibration absorption performance were investigated with numerical analysis. The comprehensive property of epicycloid path model was better than circle path was illustrated.

helicopter； bifilar pendulum；vibration absorption performance ； dynamics

2016-02-26 作者简介：黄国科(1990-)，男，广东梅州人，602所硕士点研究生，主要研究方向：直升机桨毂双线摆吸振器研究。

1673-1220(2016)02-001-05

V214.3+3;TB535

A