基于离散余弦变换的图像压缩编码方法及改进

严珍珍，刘建军

(南京邮电大学 理学院，江苏 南京 210023)

基于离散余弦变换的图像压缩编码方法及改进

严珍珍，刘建军

(南京邮电大学 理学院，江苏 南京 210023)

图像压缩是图像信息传递的一个重要途径。在对图像压缩的同时，还必须保证恢复图像的质量。目前已出现多种压缩技术并且有相应的国际标准，离散余弦变换(DCT)是许多图像编码国际标准的核心。DCT作为一种有损压缩算法，压缩比较高，且压缩后的图像视觉效果明显，因而成为图像压缩的一项重要技术,被广泛应用在图像压缩领域,比如国际静态图像压缩标准和动态图像压缩标准中都采用了DCT变换。文中介绍了DCT的原理以及它在图像压缩方面的应用。比较了两种基于DCT的图像压缩编码方法，提出了一种改进的基于二维DCT的图像压缩算法。该算法通过改进DCT系数的选取方法来控制图像压缩数组的大小，提高了图像恢复质量。在MATLAB上的实验结果表明，该算法提高了压缩图像的峰值信噪比，且耗时相对较少。

图像压缩；离散余弦变换；峰值信噪比；阈值

0 引 言

在当今信息化社会，大数据量的图像信息会给存储器的存储容量和计算机的处理速度增加很大的压力。如何高效地存储和传输图像信息将是面临的一个重要问题。对图像信息进行压缩是一种很好的解决途径。图像压缩即用少量的数据比特有损或无损地表示原始图像的技术[1]。图像压缩编码技术主要基于以下两个原理：

(1)数字图像的相关性。在一幅图像中相邻帧对应的像素之间往往相关性很强，减少图像信息中的冗余度就可以实现图像的压缩；

(2)人的视觉特征。利用人的视觉对边缘急剧变化不敏感以及对颜色分辨力弱的特点，可以在适当降低编码精度的情况下不影响总体视觉效果。

图像压缩有很多种方法，如离散余弦变换法、分形法和小波变换法等[2]。离散余弦变换(DCT)属于正交变换[3]，图像经过DCT变换后大部分能量集中在少数的系数上，并且大部分在图像块的左上角，因而是对语音和图像信号进行变换的一项重要技术。从原理上讲可以对整幅图像进行DCT变换，但是由于图像各部分上的细节程度不一样，对整体进行变换的效果不好。很多研究人员对此做了改进，比如对图像进行分块处理[4]。

文中提出一种基于DCT的图像压缩编码方法，通过改进离散余弦变换系数的选取方法来控制图像压缩数组的大小。利用Matlab进行实验，结果显示改进算法具有较好的压缩效果，且算法耗时相对较短。

1 基于二维DCT的图像压缩

1.1 二维DCT变换基本原理

离散余弦变换是一种与傅里叶变换相关的数学运算。在傅里叶级数展开式中，如果展开的函数是实偶函数，则傅里叶级数中只包含余弦项，再进行离散化就可以导出余弦变换，因此称之为离散余弦变换。二维DCT的解析式如下[5]：

设f(k,l)为二维离散函数，k,l=0,1,…,N-1，进行离散变换后：

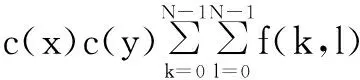
(1)

其反变换为：

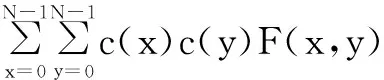
(2)

其中，k,l=0,1,…,N-1；c(x)=c(y)=

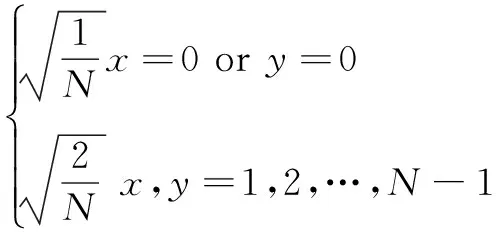
1.2 DCT的压缩过程

图像压缩分为三个过程。首先是对图像进行DCT变换，正交变换编码的基本思想是将图像编码变换到频域上进行。由于图像各个部位上的细节丰富程度有所不同，若对整幅图像进行DCT变换，恢复后的图片质量不好[6]。因此将图像分割为8×8的子块，对每个子块进行二维DCT变换。从图1中可以看到，图像的左上角亮度较高，所以DCT变换后能量主要集中在左上角的低频分量中[7]。由于左上角对应的DCT系数比较大，而右下角区域的高频细节分量对应的DCT系数较小，这样就能只编码和传输少数系数而不严重影响图像质量[8]。

其次是对变换后的DCT系数进行量化，它是一个非常重要的过程，是信息损失的根源[9]。在压缩算法中通常使用均匀量化器，具体的量化定义为：对变换后8×8子块中的DCT系数除以其量化步长，然后四舍五入。量化表达式为：

图1 图像频谱图

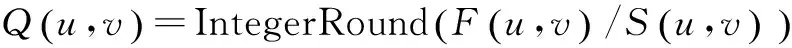
(3)

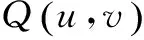
在量化过程中，高频部分的量化阈值比较大，目的是尽可能将高频部分系数转化为0；低频部分的量化阈值比较小，目的是尽可能保留图像主要能量。

最后是对量化后的系数进行编码。目前的编码方法有很多种，常用的编码方法有预测编码[11]、变换编码[12]和统计编码[13]等等，而DCT变换应用的就是变换编码。变换编码并不是直接对空域图像信号进行编码，而是先将空域图像信号变换到频域中，产生一些变换系数，然后对这些变换系数进行编码处理。

离散余弦变换编码的基本原理框图如图2所示。

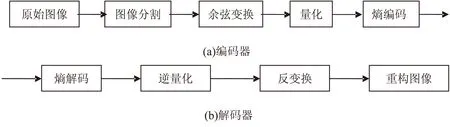
图2 离散余弦变换编码的基本原理框图

1.3 基于DCT变换的图像压缩

从图1可以看出，图像的左上角亮度较高，由于DCT变换后能量主要集中在左上角的低频分量中，对应的DCT系数比较大。为了达到图像压缩的目的，在压缩过程中可以只保留较大的DCT系数，忽略较小的DCT系数。

一种方法是只保留每个子块DCT系数矩阵的左上角10个DCT系数，其余系数全部归为0，这种方法是根据矩阵分块的思路实现的，也称为间接实现算法[14]，文中记为算法一。在一般情况下恢复的图像在视觉效果不会有太大影响，但是图像丢失的信息较多。

另一种方法是对DCT变化后的矩阵采用一致量化器量化，通过产生一个二维DCT变换矩阵，对变换后的系数矩阵进行量化，然后设定阈值来减少非零系数，对于小于设定阈值的归零处理[5]，文中记为算法二。此算法在图像恢复时容易出现块效应。

2 基于DCT变换图像压缩算法的改进

2.1 算法思想及步骤

对图像而言，低频DCT系数一般包含图像的大部分能量，因此低频系数比高频系数更为重要，但是完全放弃高频系数会使图像丢失太多信息。比如说在只留有少量的低频系数的时候，忽略高频系数可能会丢失一些具有相对能量较高的中高频系数。该算法首先将图像分割为8×8的子块，对每个子块进行二维DCT变换；在系数的选取上，保留系数矩阵左上角的10个系数，对剩下的54个系数设定阈值，对小于指定阈值的做0处理；最后把筛选的DCT系数进行整合。将这种改进算法记为算法三。

算法三的具体过程如下：

(1)将图像划分为8×8的像素子块，对每个子块进行离散余弦变换；

(2)DCT变换之后得到DCT系数矩阵，保留系数矩阵的左上角10个系数，然后对剩下54个系数设定阈值进行截断处理，对于小于指定阈值的系数归0处理，大于指定阈值的保持不变；

(3)对变换系数进行编码处理，经过编码后，每个图像块都和码书中的某个码字相对应。

2.2 MATLAB程序实现及效果分析

图像压缩要有评价标准，主要包括编码复杂度、图像恢复质量和所消耗时间等。常用的图像恢复质量的度量标准如峰值信噪比[15]：

(4)

实验采用400×400的Lena图，利用Matlab工具对图像进行仿真。下面从峰值信噪比和算法用时两个方面对上述三种算法作比较，见图3。

从图像的主观视觉效果来看，恢复质量都不错，算法二中恢复的图像相对较差一些，出现了块效应。为了直观显示DCT压缩的效果，图3(d)为算法三中图像压缩后的数据图像。

表1显示了上述三种算法的耗时和峰值信噪比。

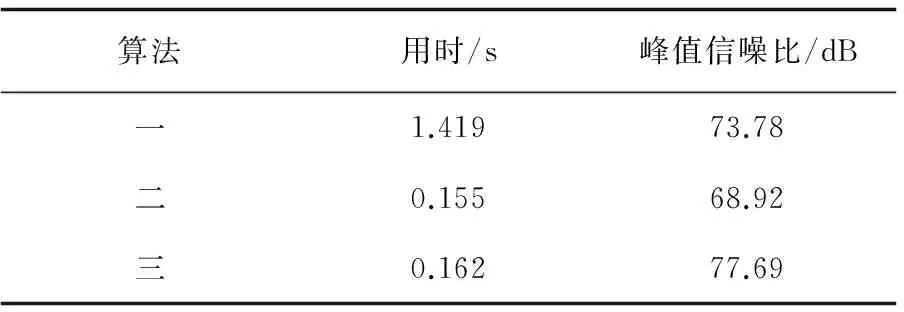
表1 三种算法的耗时和峰值信噪比

图3 实验图像

可以看出，算法二峰值信噪比是比较低的，算法三的峰值信噪比得到了较大提高。算法一耗时最长，算法二和算法三耗时较短，并且二者用时不相上下。

通过以上主观视觉效果、峰值信噪比及用时等方面的综合比较来看，基于DCT图像压缩编码的改进算法，提高了图像的恢复质量，而消耗时间也相对较短，达到了比较理想的压缩效果。

3 结束语

DCT用少量的数据点表示原图像，具有算法简单和易于实现等优点，它是图像压缩的一项重要技术。但是由于分块时块与块的边界相关性不能去掉，所以在低比特率条件下会出现块效应[16]。文中对已有的两种算法进行实现，并提出了一种基于DCT图像压缩编码的改进算法。将三种算法用Matlab编程进行实验，结果表明这种改进算法的耗时相对较少，并且图像的恢复质量最好。

[1] 高国芳.数字图像压缩处理技术[J].重庆科技学院学报:自然科学版,2006,8(2):93-95.

[2] 张兆礼.现代图像处理技术及Matlab实现[M].北京:人民邮电出版社,2001.

[3] Chen Wen-Hsiung,Smith C,Fralick S.A fast computational algorithm for the discrete cosine transform[J].IEEE Transactions on Communications,1977,25(9):1004-1009.

[4] 李高平.分形法图像压缩编码[M].西安:西安交通大学出版社,2010.

[5] Zhao Debin,Zhang Dapeng,Gao Wen.Embedded image coding based on hierarchical discrete cosine transform[J].Journal of Software,2001,12(9):1287-1294.

[6] 张 岩.MATLAB图像处理[M].北京:人民邮电出版社,2014.

[7] 陈守吉,张立明.分形与图像压缩[M].上海:上海科技教育出版社,1998.

[8] 张巧芳,李光耀,丁美林,等.基于单幅图像的三维浏览图生成算法[J].计算机技术与发展,2010,20(1):22-24.

[9] 赵 珊,赵 倩.基于DCT系数的JPEG图像检索算法[J].计算机工程,2010,36(19):190-192.

[10] 阮秋奇.数字图像处理学[M].北京:电子工业出版社,2001.

[11] Li Y,Gong P,Sasagawa T.Integrated shadow removal based on photogrammetry and image analysis[J].International Journal of Remote Sensing,2005,26(18):3911-3929.

[12] Tsai V J D.A comparative study on shadow compensation of color aerial images in invariant color models[J].IEEE Trans on Geoscience and Remote Sensing,2006,44(6):1661-1671.

[13] 卢佩新，赵国安.基于终端-服务器模式的扫描仪图像获取技术[J].计算机技术与发展,2010,20(3):28-31.

[14] 李秀敏,万里青,周拥军.基于Matlab的DCT变换在JPEG图像压缩中应用[J].电光与控制,2005,12(2):64-67.

[15] 王爱玲,叶明生,邓秋香.MATLAB2007图像处理技术与应用[M].北京:电子工业出版社,2008.

[16] Xiong Z,Ramchandran K,Orchard M,et al.A comparative study of DCT and wavelet-based image coding[J].IEEE Trans on Circuits System Video Technology,1999,9(8):692-695.

Improved Image Compression Coding Method Based on Discrete Cosine Transform

YAN Zhen-zhen,LIU Jian-jun

(College of Science,Nanjing University of Posts and Telecommunications,Nanjing 210023,China)

Image compression is an important way of image information transfer.The quality of image must be ensured when it is compressed.Among kinds of compressing methods,Discrete Cosine Transform (DCT) is the core of most international image compressing standards.As a lossy compression algorithm,DCT can achieve high compression ratio and good visual effect.So the method becomes an important technology of image compression and it has been widely used in the areas such as image compression,especially in the JPEG and the MPEG.The principle of DCT and its applications in image compression are introduced in this paper.Based on comparison of two kinds of image compression based on DCT,an improved image compression method based on DCT is proposed.By choosing coefficient of DCT to control the size of an array of image compression,the new method improves the quality of image restoration.The experiments of MATLAB show that the proposed algorithm improves the PSNR of compressed images and consumes relatively few time.

image compression;discrete cosine transform;PSNR;threshold

2015-04-30

2015-08-05

时间：2016-01-04

国家自然科学基金资助项目(11471114，61179027)

严珍珍(1978-)，女，副教授，研究方向为动力系统、分形和非线性分析；刘建军(1991-)，男，研究生，研究方向为非线性分析。

http://www.cnki.net/kcms/detail/61.1450.TP.20160104.1453.020.html

TP301.6

A

1673-629X(2016)01-0147-03

10.3969/j.issn.1673-629X.2016.01.031