基于遗传算法优化的LS-SVM井下场强预测
2016-02-22王安义郗茜
王安义, 郗茜
(西安科技大学 通信与信息工程学院, 陕西 西安 710054)
基于遗传算法优化的LS-SVM井下场强预测
王安义, 郗茜
(西安科技大学 通信与信息工程学院, 陕西 西安 710054)
为了进一步研究井下电波传播损耗规律,提高场强覆盖预测准确度,提出使用基于遗传算法优化的最小二乘支持向量机方法对井下巷道的场强进行预测。首先通过软件仿真生成巷道场强数据,并将数据分为训练集和测试集;然后采用最小二乘支持向量机方法对训练集进行学习,并使用遗传算法对最小二乘支持向量机方法的参数选择进行优化,采用测试集对方法性能进行验证;最后将基于遗传算法优化的最小二乘支持向量机方法用于井下巷道的场强预测。仿真实验结果表明,基于遗传算法优化的最小二乘支持向量机方法能够有效提高井下场强预测的精度,可获得较好的预测效果。
矿井巷道; 场强预测; 最小二乘支持向量机; 遗传算法
0 引言
随着移动通信和无线技术的发展,井下无线通信系统的研究越来越受到重视。但是,由于矿井巷道地质地形结构复杂、工作环境恶劣,无线电波在传播过程中存在严重的反射、绕射、散射现象,与在地面及受限的地面空间中有较大差异[1-2],使得井下无线通信系统的建立面临较大困难。
为了进一步研究井下电磁波传播损耗规律,提高矿井场强预测的准确度,进而为建立井下无线通信系统提供可靠的理论基础,国内外研究人员进行了大量的研究。参考文献[3]给出了900 MHz无线电波在煤矿井下传播的双斜率模型,参考文献[4]给出了高速铁路隧道无线电波传播的对数损耗校正模型。然而由于井下环境复杂多变,上述模型只适用于特定情况,不能较好地反映信道场强的非线性特性,存在预测精度低的问题。参考文献[5-6]提出利用神经网络分别建立电磁传播预测模型和场强覆盖预测方法,但是神经网络存在学习收敛速度慢、容易陷入局部最优的问题。
针对以上问题,本文采用基于遗传算法(Genetic Algorithm,GA)优化的最小二乘支持向量机(Least Square Support Vector Machine,LS-SVM)方法对井下场强进行预测。
支持向量机(Support Vector Machine,SVM)能够克服神经网络训练时间长、预测结果过拟合等不足,是目前机器学习的研究热点,在很多领域都得到了成功应用。与标准支持向量机相比,LS-SVM改变了约束条件和损失函数,使得标准SVM中的凸二次规划问题转变为对一组线性方程的求解,从而在一定程度上降低了问题的复杂度,加快改变了约束条件和损失函数,加快了运算处理速度[7]。
同其他学习算法一样,SVM的性能依赖于学习机的参数,然而到目前为止并没有指导LS-SVM参数选择的好方法[8],主要是依靠交叉验证、实验对比或者其他统计方式来确定。鉴于遗传算法具有良好的全局寻优能力,本文选择使用遗传算法来优化求解LS-SVM相关参数。首先通过仿真软件得到井下巷道场强的模拟数据,然后使用基于GA优化的LS-SVM方法对矿井巷道场强进行预测。
1 LS-SVM原理
SVM基本思想是通过非线性映射将输入向量映射到高维特征空间,将非线性估计问题转化为特征空间的线性估计问题。LS-SVM将最小二乘法引入到SVM,降低了计算复杂性。
训练集T={(xi,yi),i=1,2,…,N},其中xi∈Rn,为输入向量;yi∈R,为输出向量;N为训练集包含的样本数;n为xi的维数。利用非线性映射φ(·)将样本从原空间Rn映射到特征空间φ(xi),在高维特征空间中构造最优决策函数:
y(x)=ωT·φ(x)+b
(1)
式中:ω为超平面权值特征向量;b为偏置项。
利用结构最小化原则,寻找最优的参数ω,b,LS-SVM优化问题表示为[9]
s.t.yi=ωTφ(xi)+b+ξi,i=1,2,…,l
(2)
式中:γ为正则化参数;ξi为误差变量。
用拉格朗日法求解上述优化问题:

(3)
式中αi为拉格朗日乘子。
根据KKT条件分别对ω,b,ξi,αi求偏导,并消去ω和ξ,得到如下矩阵的形式:
(4)
式中:v=[1 1 … 1]T;I为N阶单位矩阵;α=[α1α2…αN];Y=[y1y2…yN]T;K为N阶方阵,其第i行第j列的元素Kij=φ(xi)T×φ(xj)=K(xi,xj)。
K(·,·)为核函数,常用的核函数有多项式核函数、径向基(RBF)核函数、Sigmoid核函数等。本文采用径向基核函数,如式(5)所示。
(5)
式中:xi,xj为训练输入样本;σ为径向基的宽度,为待定参数。
在核函数和训练样本确定后,LS-SVM的性能就取决于正则化参数γ和核函数的参数σ。其中γ用来控制模型复杂度和精度之间的折衷,σ用于控制支持向量的个数和泛化能力[10]。
使用最小二乘法求出α和b,由此得到LS-SVM预测输出为
(6)
2 GA优化LS-SVM方法在井下场强预测中的应用
遗传算法的基本思想是模拟自然界遗传机制和生物进化论而形成的一种过程搜索最优解的算法[11],它是一种具有自适应能力的全局性的概率搜索算法。根据适应度函数,通过复制、交叉、变异对个体进行迭代筛选,直到满足一定的条件。使用GA优化的LS-SVM方法对井下场强进行预测的步骤如下:
(1) 对矿井巷道环境进行分析研究,选择合适的SVM回归模型。
(2) 通过软件仿真生成实验数据,对接收功率数据进行预处理,主要处理异常数据和缺失数据,并对数据进行归一化处理。
(3) 将一部分仿真数据作为训练样本,另一部分作为测试样本,构造输入输出变量。
(4) 使用LS-SVM对训练数据进行学习,并使用GA算法对LS-SVM的参数进行优化,优化步骤如下:① 选择编码策略,将解空间中的数据映射到遗传空间,初始化参数γ和σ,并对γ和σ进行二进制编码。② 设置遗传算法的各种参数,包括种群个数、进化最大迭代次数、交叉概率、变异概率等。③ 随机初始化产生初始种群,将交叉训练的均方误差作为适应度值,计算个体适应度。④ 按照遗传策略进行选择、交叉、变异操作,形成下一代种群。⑤ 判断种群是否达到最大遗传代数或者是否满足设定的精度要求,若已经满足则完成,若不满足则返回执行步骤④。⑥ 输出最优个体的解码,并将它作为问题的最优解。
(5) 利用测试集评价预测性能的好坏,并与传统方法进行比较。
应用基于GA优化的LS-SVM方法预测井下场强的流程如图1所示。
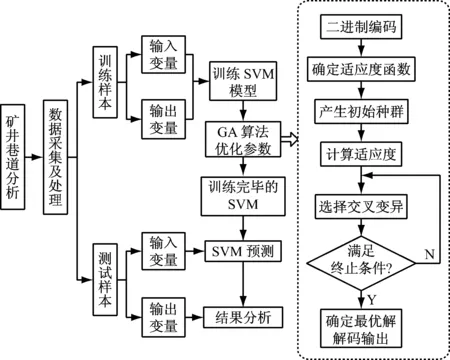
图1 应用基于GA优化的LS-SVM方法预测井下场强的流程
3 仿真实验及分析
3.1 实验数据产生
实验仿真数据由软件生成,巷道形状采用半圆拱形,截面示意如图2所示。将巷道看作不规则的长波导,巷道内部不填充任何介质,仿真参数设置见表1。

图2 半圆拱形巷道截面
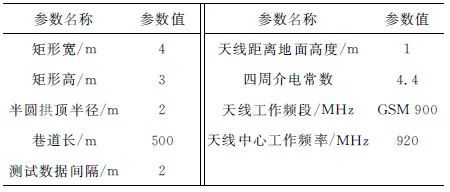
表1 仿真参数设置
假设巷道长为500 m,每隔2 m设置一个测量点,共251个测量点,每个点记录20次测量数据。为了保证数据的有效性,有必要对数据进行预处理,滤除快衰落的影响,对每个测量点的数据进行算术平均,最后得到251个测量点的平均接收功率,如图3所示。在仿真中使用前150个数据作为训练集,后101个数据作为测试集。

图3 接收功率分布
3.2 仿真实验
仿真实验中遗传算法的参数设置如下:种群数为50,进化最大迭代次数为200,交叉概率为0.25,变异概率为0.005,采用二进制编码。利用遗传算法求解得到γ= 6.633 19,σ= 0.301 361,将参数代入式(4)可以求得α和b,并得到预测输出。图4给出了经GA优化的LS-SVM的井下场强预测的实际值与预测值曲线,可以看出使用该算法的预测值和实际值的契合度较好。
为了验证本文方法的有效性,同时使用小波神经网络(WNN)、标准LS-SVM对井下场强进行预测。小波神经网络是小波分析和神经网络相结合的产物,其整个结构依据小波分析理论确定,网络结构更简单。但是它也存在不足,例如隐含层节点数难以确定,随着输入维度增加,网络训练样本指数也增加等。小波神经网络隐含节点个数设置为6,网络迭代学习次数为100。3种算法101个预测点的实际值和预测值曲线如图5所示,3种算法实际值和预测值之间的误差曲线如图6所示。

图4 基于GA优化的LS-SVM场强预测效果
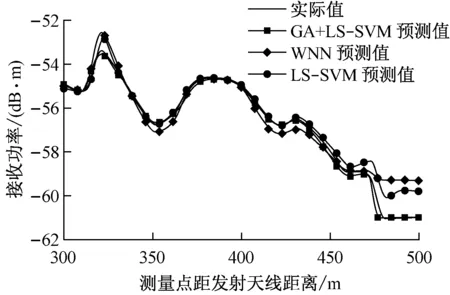
图5 3种预测方法101个预测点的实际值和预测值曲线

图6 3种预测方法实际值和预测值之间的误差曲线
使用预测值和实测值之间的平均绝对误差(MAE)、均方根误差(RMSE)和相关系数r作为模型预测性能的评价指标,3个指标的定义分别如式(7)—式(9)所示。
(7)
(8)
(9)
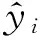
MAE和RMSE越小说明误差越小,预测结果越好;而r越大说明预测值与实际值越接近。3种预测方法的性能比较结果见表2。
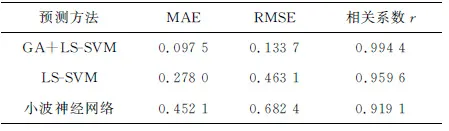
表2 3种预测方法性能比较结果
由图5和图6可以看出,经GA优化的LS-SVM方法能够更精确地对井下巷道场强进行预测,预测值更加接近实测值,预测误差也明显小于其他2种方法。而且从表2可以看出,经GA优化的LS-SVM建立的回归预测模型的平均绝对误差相对其他2种方法小了一个数量级,相关系数也较高,说明经GA优化的LS-SVM预测方法能够有效地提高井下场强预测的精度,获得更好的预测效果。
4 结语
基于遗传算法优化的LS-SVM井下场强预测方法使用最小二乘支持向量机对井下巷道场强进行预测,应用遗传算法对支持向量机的正则化参数γ和核函数的参数σ进行参数寻优。仿真结果表明,与已有的小波神经网络和普通LS-SVM预测方法相比,使用基于GA优化的LS-SVM预测方法具有更高的精度和泛化能力,是一种可行的井下巷道场强预测方法。目前,该方法的样本数据的代表性还不够,未来还需进一步改进,使其在井下场强预测中具有更广泛的适应性。
[1] 曹育红.矿井无线通信系统的频率选择[J].工矿自动化,2005,31(4):38-40.
[2] 张申.隧道无线电射线传输规律的研究[J].电波科学学报,2002,17(2):114-118.
[3] 张跃平,张文梅,郑国莘,等.预测隧道中传播损耗的混合模型[J].电子学报,2001,29(9):1283-1286.
[4] 余晨辉.高速铁路隧道无线传播损耗模型校正[J].移动通信,2007,31(12):73-76.
[5] 唐秋菊,徐松毅.基于神经网络的传播预测模型浅析[J].无线电工程,2010,40(3):21-23.
[6] 关捷,李国宁,温宇钧.基于GRNN的GSM-R场强覆盖预测算法[J].铁道标准设计,2014,34(2):106-112.
[7] 张学工.关于统计学习理论与支持向量机[J].自动化学报,2000,26(1):36-46.
[8] 郭辉,刘贺平,王玲.最小二乘支持向量机参数选择方法及其应用研究[J].系统仿真学报,,2006,18(7):2033-2036.
[9] SUYKENS J A K,VANDEWALLE J.Least squares support vector machine classifiers[J].Neural Processing Letters,1999,9(3):293-300.
[10] 王安义,郭世坤.基于LS-SVM的矿井巷道场强预测[J].工矿自动化,2014,40(10):36-40.
[11] 边霞,米良.遗传算法理论及其应用研究进展[J].计算机应用研究,2010,27(7):2425-2429.
Forecasting of underground field intensity based on LS-SVM optimized by genetic algorithm
WANG Anyi, XI Xi
(School of Communication and Information Engineering, Xi'an University of Science and Technology, Xi'an 710054, China)
In order to study propagation loss law of electric wave and improve prediction accuracy of field intensity coverage in mine tunnel, least square support vector machine (LS-SVM) method optimized by genetic algorithm was used to forecast underground field intensity in mine tunnel. Firstly, simulated field intensity data was generated by computer software and divided into training set and testing set. Then the LS-SVM machine method was used to study training set, genetic algorithm was used to optimize parameters of LS-SVM, and testing set was used to verify performance of the method. Finally the LS-SVM method optimized by genetic algorithm was used to forecast underground field intensity in mine tunnel. The simulation and experiment results prove that the LS-SVM optimized by genetic algorithm can effectively improve prediction accuracy of field intensity in mine tunnel, and achieve good prediction effect.
mine tunnel; field intensity forecasting; least square support vector machine; genetic algorithm
2016-06-22;
2016-08-19;责任编辑:张强。
陕西省自然科学基础研究计划资助项目(S2015YFJM1734)。
王安义(1968-),男,山东潍坊人,教授,博士,主要研究方向为无线传播与矿井通信技术,E-mail:wanganyi@xust.edu.cn。
1671-251X(2016)12-0046-05
10.13272/j.issn.1671-251x.2016.12.010
TD655
A
时间:2016-12-01 10:31
http://www.cnki.net/kcms/detail/32.1627.TP.20161201.1031.010.html
王安义,郗茜.基于遗传算法优化的LS-SVM井下场强预测[J].工矿自动化,2016,42(12):46-50.
