湍流边界层厚度对三维空腔流动的影响
2016-02-22刘俊杨党国王显圣罗新福中国空气动力研究与发展中心空气动力学国家重点实验室绵阳621000
刘俊, 杨党国, 王显圣, 罗新福 中国空气动力研究与发展中心 空气动力学国家重点实验室, 绵阳 621000
湍流边界层厚度对三维空腔流动的影响
刘俊*, 杨党国, 王显圣, 罗新福 中国空气动力研究与发展中心 空气动力学国家重点实验室, 绵阳 621000
采用脱体涡模拟(DES)方法开展了不同湍流边界层厚度(TTBL)下的三维空腔非定常流动数值计算。空腔长、宽、深比例为5∶1∶1,来流马赫数为0.85,雷诺数为13.47×106m-1,各工况湍流边界层厚度比值为1∶2∶4∶8。研究结果表明,湍流边界层厚度对自由剪切层的发展、空腔底部静态压力分布、脉动压力及空腔流动类型均有重要影响,且随着边界层厚度的增大,下游剪切层覆盖的范围会增大,但是剪切层增长率降低;空腔前后静态压力压差减小、压力梯度下降;腔内局部测点的脉动压力声压级下降,各阶声压峰值频率向低频方向偏移;空腔流动类型往开式流动方向转换。
脱体涡模拟; 湍流边界层厚度; 三维空腔; 非定常流动; 流动类型
随着空腔构型在航空航天领域中应用越来越广泛,空腔非定常流动已成为先进飞行器研发中的常见气动问题。如战斗机内埋武器舱打开后,舱内会产生强烈的压力脉动,可能诱发武器舱薄壁结构的疲劳破坏以及舱内电子器件的失灵失效。民用客机起飞和着陆时,起落架舱是主要噪声源之一,若不能有效控制其辐射噪声,将制约客机的适航取证。超燃冲压发动机燃烧室内用于稳定火焰的凹腔,若设计不当,不仅会降低燃烧效率,甚至还可能导致熄火,迫使发动机停车[1]。另外,航天飞机表面的凹陷在一定条件下,可能促发转捩,使局部热流增大,导致表面热防护材料失效,酿成发射事故[2]。除了以上几种典型情况,空腔在其他方面也有大量的应用。因此开展空腔流动特性研究,有助于加深对空腔复杂流动的认识,改进空腔气动设计,解决空腔复杂流动诱发的噪声、振动以及分离等一系列问题。
空腔流动涉及剪切层和旋涡的形成与发展,旋涡与固壁的碰撞,激波/旋涡/剪切层的相互作用,流动自激振荡和声腔共鸣等,牵扯到流动、噪声两个物理场的耦合作用,是一种十分复杂的气动现象。研究表明,影响空腔流动特性的因素非常多,如空腔几何外形、来流马赫数、雷诺数以及来流边界层等。
来流边界层是形成空腔上方剪切层的源头,对下游剪切层及旋涡的形成与发展都有重要影响,是影响空腔流动特性的关键因素之一。边界层流动形态的转换(层流、湍流)、边界层厚度变化、边界层内速度型的变化等均可能对空腔流动的发展产生影响。以内埋武器舱为例,武器舱安装在后掠翼下方时,受横流干扰,边界层内会诱导出展向速度分量,呈现三维效应;安装在腹部时,由于机头比进气道更早接触气流,边界层发展不同步,边界层厚度呈现出中间高两边低的非均匀分布;另一方面,随着飞行高度的变化,边界层厚度也会随之改变。来流边界层的非均匀分布会促使内埋武器舱流动表现出更为强烈的三维效应,进一步加大噪声特性的预测难度;而边界层厚度变化不仅会改变舱内流动和噪声特性,也可能影响相关控制技术在内埋武器舱中的应用效果。因此,开展来流边界层特性对空腔流动的影响研究对于以内埋武器舱为代表的空腔类部件的气动外形优化设计、流动控制措施开发、控制效果评估及优化等都具有十分重要的意义。
在试验研究方面,国内外开展空腔类风洞试验时,主要采取两种安装方式[3-7]。一种是通过尾撑或腹撑方式将空腔模型安装在风洞核心流中,空腔前缘由一块切尖平板发展来流边界层,由于风洞堵塞度的限制以及模型结构刚度的要求,平板和空腔模型尺寸不能太大,可模拟的边界层厚度及雷诺数范围受到限制。另一种是将空腔模型安装在风洞试验段侧壁上,这样空腔模型不受风洞堵塞度的影响,可以将尺寸做得更大,同时也有利于测试设备的安装和使用。但是,由于边界层沿着风洞壁面自由发展,在一定试验条件下边界层厚度也是一定的,难以模拟真实飞行的边界层状况。在国外,利用试验手段开展边界层影响研究较少,具有代表性的工作是Plentovich[6]在平板上粘贴不同宽度的粗糙带形成了不同厚度湍流边界层,并研究其对空腔流动的影响规律。在国内,杨党国等[8-9]通过对比空腔模型安装在风洞侧壁和核心流中2种不同情况,分析了边界层厚度变化对亚、跨声速和超声速空腔流动特性的影响。
在数值研究方面,国内外对空腔流动开展了大量的研究,但研究关注点主要集中在马赫数、长深比等参数变化对空腔流动特性的影响[10-11]和前缘扰流、后缘修型等被动流动控制措施[12-15],以及对空腔噪声产生机理的探索[16-21]等方面,关于边界层厚度变化的影响研究尚不充分。
本文利用数值模拟方法在改变空腔前缘来流边界层厚度等参数的易实现性和可行性的前提下,采用延迟脱体涡模拟(DDES)方法研究了马赫数0.85条件下,湍流边界层厚度变化对三维空腔非定常流动的影响规律。
1 数值方法
采用有限体积法求解三维非定常Navier-Stokes控制方程,采用二阶迎风格式计算界面对流通量,确保计算的稳定性, 黏性通量则采用二阶中心离散,尽量降低数值耗散。时间推进采用二阶向后差分格式,保证非定常计算结果的时间精度,内迭代运用多重网格技术加速收敛。
考虑到传统的雷诺平均Navier-Stokes (RANS)方法耗散大,难以解析小尺度湍流结构及高频信号,而大涡模拟(LES)、直接数值模拟(DNS)方法计算量大,目前的计算资源难以接受,故采用目前较为流行的脱体涡模拟(DES)方法模拟空腔的非定常流动。DES方法是RANS/LES混合算法中的一种,它吸收了RANS方法在模拟近壁湍流所需网格分辨率低以及LES方法在模拟分离区流动耗散小的优点,是一种模拟大分离流动时广泛采用的方法。
本文采用的DES方法是在Menter的剪切应力输运(SST)两方程湍流模型基础上构造而来的,其思想是保持模型中的耗散率方程不变,通过改进湍动能输运方程的耗散项实现RANS到LES的转换。修改后的湍动能方程为
(1)
lDES=min(lRANS,lLES)
(2)
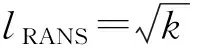
2 空腔模型及计算状态
计算所采用的空腔模型为英国的防务科学和研究机构(DERA)开发的M219空腔外形[7]。空腔长度L为0.508m,长、宽、深的比例为L∶W∶D=5∶1∶1。入口距离前缘1.45L。物面采用绝热无滑移边界条件。计算网格如图1所示,网格总量为360万,在空腔附近采用局部加密技术,空腔处网格占网格总量的30%左右。来流马赫数为0.85,雷诺数Re=13.47×106m-1,入口静压为82 100Pa,静温为266.53K。为了提高非定常流动的时间分辨率,希望时间推进步长越小越好,然而统计噪声信号又需要保证足够长的时间历程,因此时间步长又不能取得太小,根据文献[22]的推荐,选择时间步长为0.005倍无量纲时间,约为9.6×10-6s,使Rossiter一阶模态对应周期内约有700个采样点,保证了非定常流动精细模拟所需的时间精度。首先用非定常雷诺平均Navier-Stokes(URANS) 方法推进一段时间,待基本流场建立后开始DDES计算。非定常计算共推进23 000步,约0.22s,使脉动压力信号统计有足够的样本数据。空腔底部沿流向均匀布置K20~K29这10个压力监测点,如图2所示,每推进一个时间步记录一次压力数据,采样频率为104.17kHz。
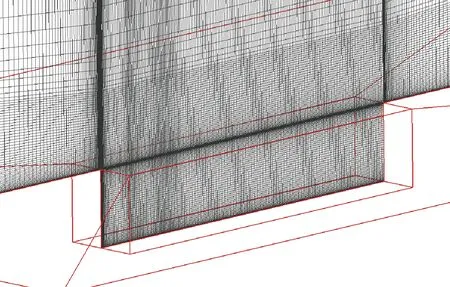
图1 计算网格
Fig.1 Computational grid
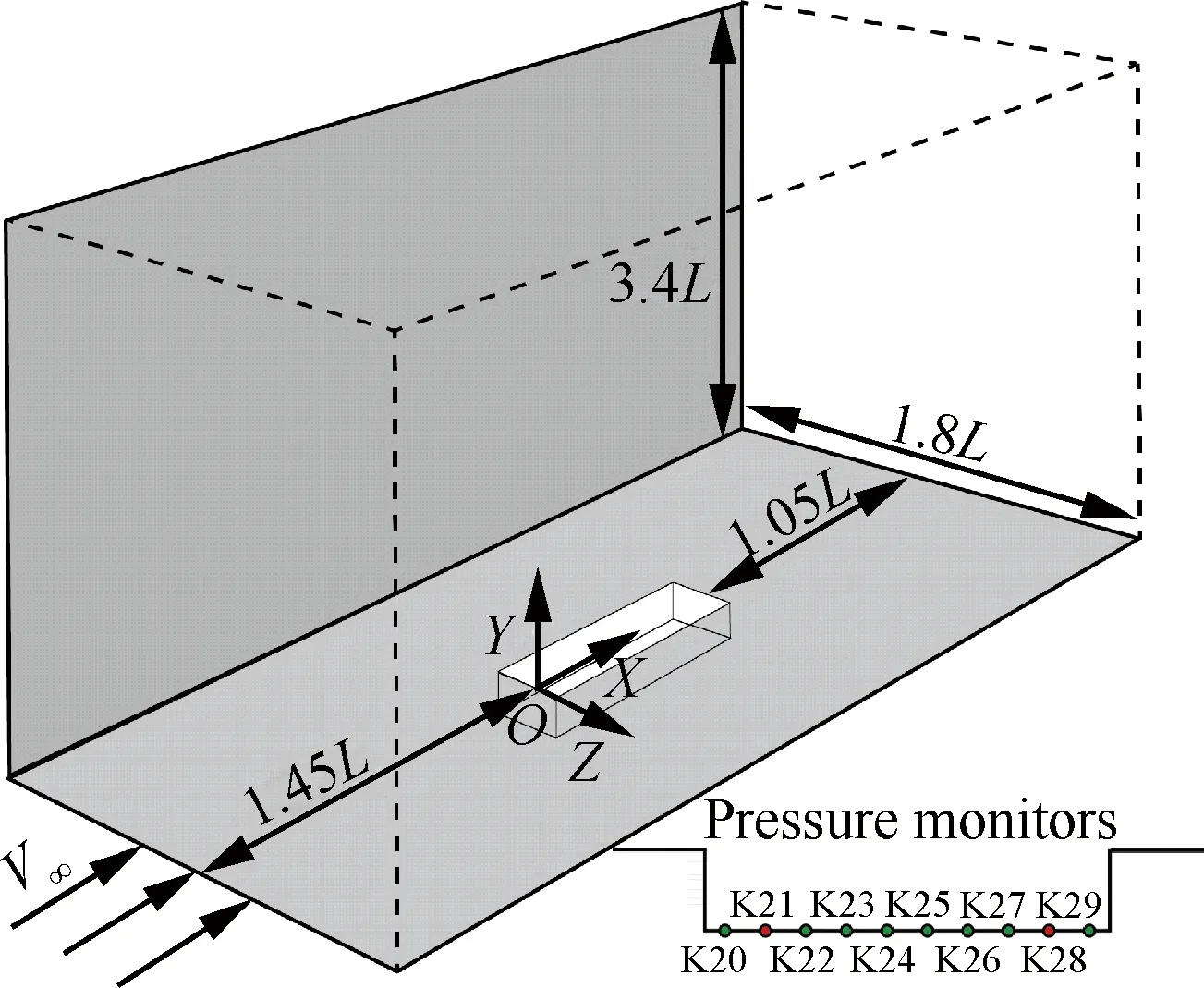
图2 三维空腔流动计算域及压力监测点
Fig.2 Computational domain of three-dimensional cavity flow and pressure monitors
在空腔流动研究中,边界层一般特指位于空腔前缘的来流边界层。本文开展边界层厚度影响研究,需要在前缘处构造出不同的边界层速度分布,若直接将计算域入口设定在空腔前缘,边界处理存在很大难度。因此,采用的方法是在空腔上游一定距离设置不同厚度湍流边界层,使下游发展出不同的边界层速度分布。采用1/7幂规律[23-26]在入口处给定湍流边界层速度剖面,即
(3)
式中:V∞为来流速度;δin为入口边界层厚度,分别设定为0.04L、0.08L和0.16L。δin为0时,入口统一为自由来流速度V∞。
3 数据处理方法及验证
3.1 数据处理方法
通过一点的时序压力采样信号,得到该点脉动压力均方根值为
(4)
式中:T为采样周期。
对应的总声压级(OASPL)为
(5)
式中:参考压力pref=2×10-5Pa。
通过对脉动压力信号进行快速傅里叶变换(FFT),得到功率谱密度(PSD)函数p(f),开展频谱分析。
(6)
式中:f为频率;t为时间。
3.2 数值方法验证
M219外形是开展空腔流动研究常用的模型之一,国外针对该外形进行了大量的风洞试验,并公开了试验数据。非定常数值计算研究领域也多采用该外形来验证数值方法的可靠性,如欧盟Desider项目中就包含M219空腔计算结果对比的研究内容。为了检验采用的数值计算方法的可行性和正确性,将计算结果与试验数据[22,27]进行了综合对比分析。
在空腔内所有的脉动压力监测点中,典型位置测点K21处脉动压力功率谱曲线在低频区域起伏较大,若对比结果良好则能很好地反映出数值计算方法的可靠性和正确性。因此,通过对比分析空腔内K21的脉动压力功率谱试验结果来验证数值计算方法。从试验和计算结果的对比来看,在低频区域离散频率上两者均出现了功率谱密度明显增大的现象,这是空腔流声耦合现象的典型特征。同时,计算得到的声压峰值频率及脉动压力幅值均与试验符合得较好。另外,还对比了空腔底部脉动压力总声压级分布,计算和试验的分布规律基本一致,计算的声压级略高于试验结果3~4 dB,如图3所示[22,27]。与试验数据的对比结果表明,本文所采用的数值方法能够捕捉到空腔流声耦合和自激振荡等主要的流动特征,计算结果与试验结果基本吻合,能够较为准确地模拟空腔非定常流动及近场噪声的特性。

图3 计算结果与试验数据对比[22,27]
Fig.3 Comparison of computational results and experimental data[22,27]
4 研究结果分析
开展了入口湍流边界层厚度δin为0、0.04L、0.08L和0.16L等条件下的空腔非定常流动特性数值计算研究,分析了来流边界层厚度变化对空腔上方自由剪切层结构、空腔流动类型、静态压力分布、脉动压力特性等的影响规律。
由于计算域入口到空腔前缘还有一段距离,随着边界层的自由发展,边界层厚度δ可能会发生变化。图4给出了从入口到空腔前缘,湍流边界层厚度的变化曲线。对于δin为0.04L,0.08L和0.16L的情况,从入口到空腔前缘,边界层厚度基本保持不变。而δin为0的情况下,随着湍流边界层的自由发展,边界层厚度线性增长,空腔前缘处边界层厚度δle为0.01 m,约为0.02L,与试验[28]测得的前缘边界层厚度0.010 7 m十分接近。4种工况在空腔前缘处的边界层厚度δle分别为0.02L、0.04L、0.08L和0.16L,比例为1∶2∶4∶8。
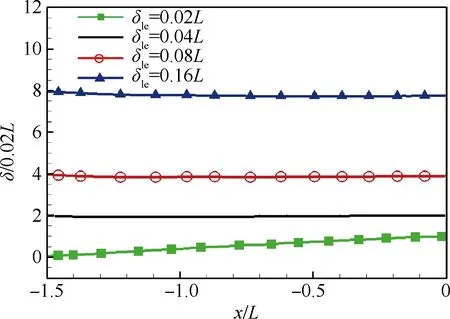
图4 入口至空腔前缘边界层厚度变化曲线
Fig.4 Variation curves of boundary layer thickness from inlet to cavity leading edge
4.1 对自由剪切层的影响
湍流边界层跨过空腔前缘角点即演变为自由剪切层,湍流边界层厚度的变化必然会对下游剪切层的发展与演化产生影响。
图5为空腔中间截面时均速度剖面分布。可以看到,不同工况下腔内速度剖面沿流向的变化规律基本一致。空腔前缘处,腔内速度接近为0,而腔外为自由来流速度,速度剖面在腔口从0直接过渡到自由来流速度,该处自由剪切层厚度与前缘边界层厚度相当。随着流动向下游发展,腔内流体在外流的带动下也流动起来,剪切流动区域扩大,剪切层法向速度梯度减小;且随着边界层厚度增大,自由剪切层覆盖的范围也越来越大。
(7)

图5 空腔中间截面时均速度剖面分布
Fig.5 Time-averaged velocity profiles on middle plane
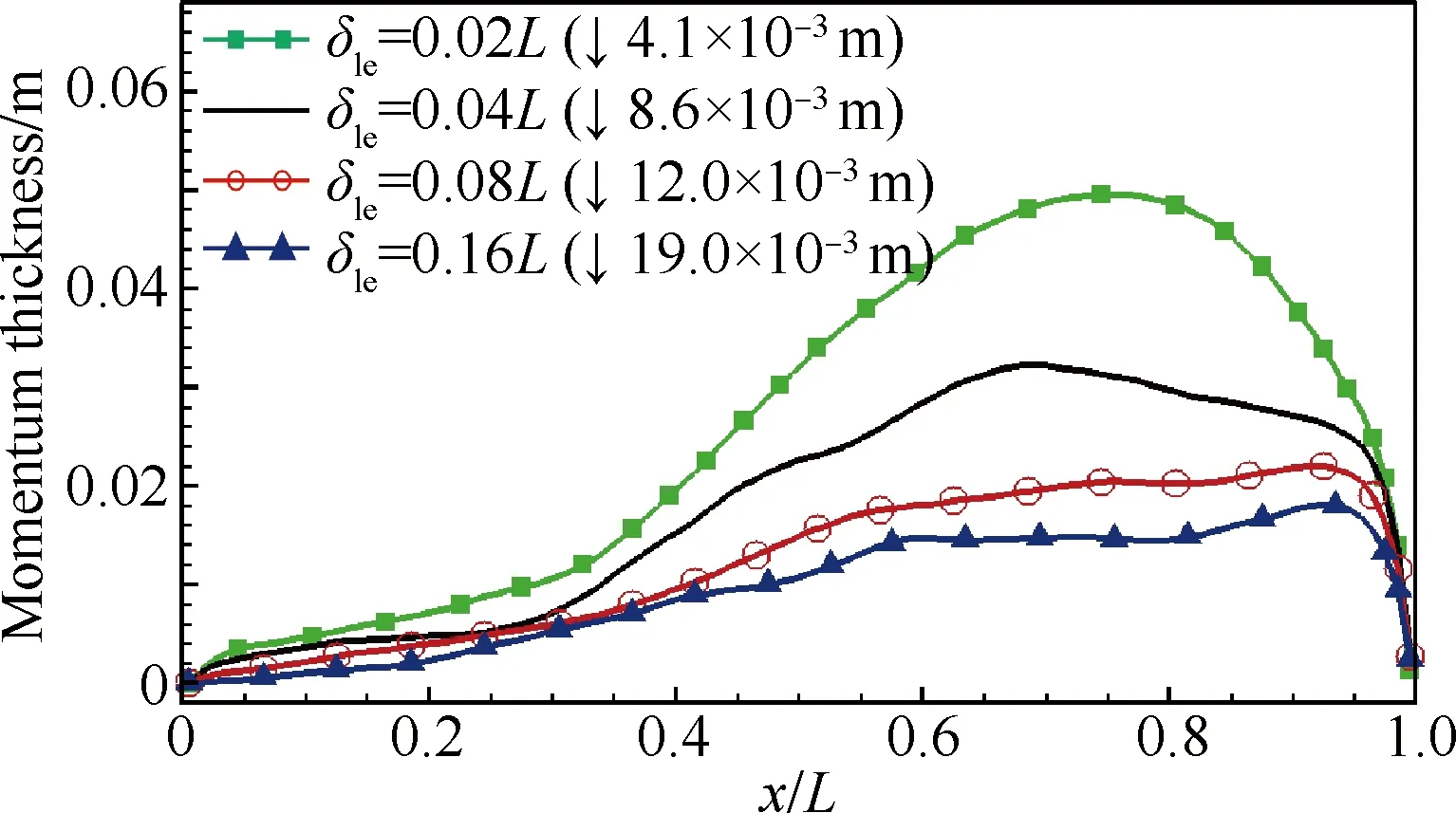
图6 空腔中间截面剪切层动量损失厚度分布
Fig.6 Momentum thickness distributions on middle plane of cavity
总之,随着边界层厚度增大,其下游剪切层覆盖的范围增大,但是剪切层增长率降低。原因分析如下:由于非均匀平行流动普遍存在的开尔文-亥姆霍兹不稳定性,剪切层在向下游对流过程中会演变成涡结构,涡结构不断增长的同时,剪切层内的速度掺混进一步加强,剪切层覆盖的区域扩大。随着湍流边界层厚度增加,自由剪切层的初始厚度随之增加,其在向下游发展的过程中覆盖的范围也会进一步增大。另一方面,剪切层、涡结构与腔后壁碰撞后会形成扰动声波,扰动声波向前传播,在空腔前缘与边界层内的不稳定波作用,会加速剪切层及涡结构的发展,从而在后壁产生更加强烈的碰撞以及更大的扰动声波,形成流声耦合回路。Vakili和Gauthier认为,边界层厚度与不稳定波之间有着密切关系,随着边界层厚度的增加,剪切层内的不稳定波特征频率会发生改变[29]。然而,不稳定波特征频率与空腔声模态频率之间的匹配程度降低,会导致扰动声波对不稳定波的激励效果减弱,进而抑制下游剪切层涡结构的增长,引起自由剪切层的增长率下降。
4.2 对静压分布的影响
静压分布是描述空腔平均流动特性的重要指标,也是判定空腔流动类型的关键依据。图7给出了不同边界层厚度情况下,空腔底部的压力系数Cp分布,可以看到,各种工况下压力系数分布的规律保持一致,在空腔前缘腔内压力系数从0开始缓慢下降,在x/L=0.4附近压力系数降到最低值,随后压力系数开始抬升,快接近腔后部时,压力系数下降或维持不变,最后在后缘处压力系数又迅速提升,达到最大值。随着边界层厚度的增加,尾缘处的最大压力降低,位于中部的最小压力系数升高,压差减小,同时抬升段的压力梯度也明显下降。
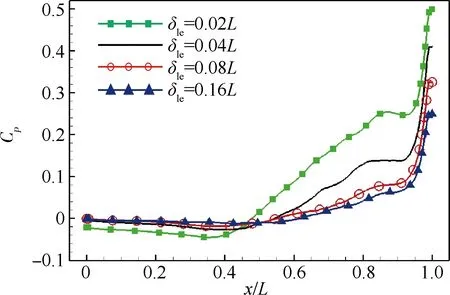
图7 空腔底部压力系数分布
Fig.7 Distributions of pressure coefficient at bottom of cavity
空腔前后压差减小,对于降低空腔类构型飞行器的气动阻力十分有利。而对于内埋武器系统,压力梯度的降低也会减小作用在舱内武器上的俯仰力矩,有助于改善内埋武器安全分离特性。
4.3 对脉动压力的影响
空腔流动的一个显著特点就是流动呈现高度非定常、非线性,流动与噪声相互耦合,压力脉动异常强烈,而压力周期性脉动有可能引起结构共振,造成不可逆转的结构损伤,因此空腔的脉动压力特性受到越来越广泛的关注。
图8为腔底部脉动压力总声压级的分布,可看出随着空腔前缘来流边界层厚度的增加,腔内总声压级分布呈整体平移下降,δle=0.16L工况较δle=0.02L最多降低了6 dB。从4.1节分析可知,边界层厚度的增加导致不稳定波特征频率与空腔声模态频率之间的匹配程度降低,使得扰动声波对不稳定波的激励效果下降,从而削弱流声耦合放大效应,腔内压力脉动被抑制。
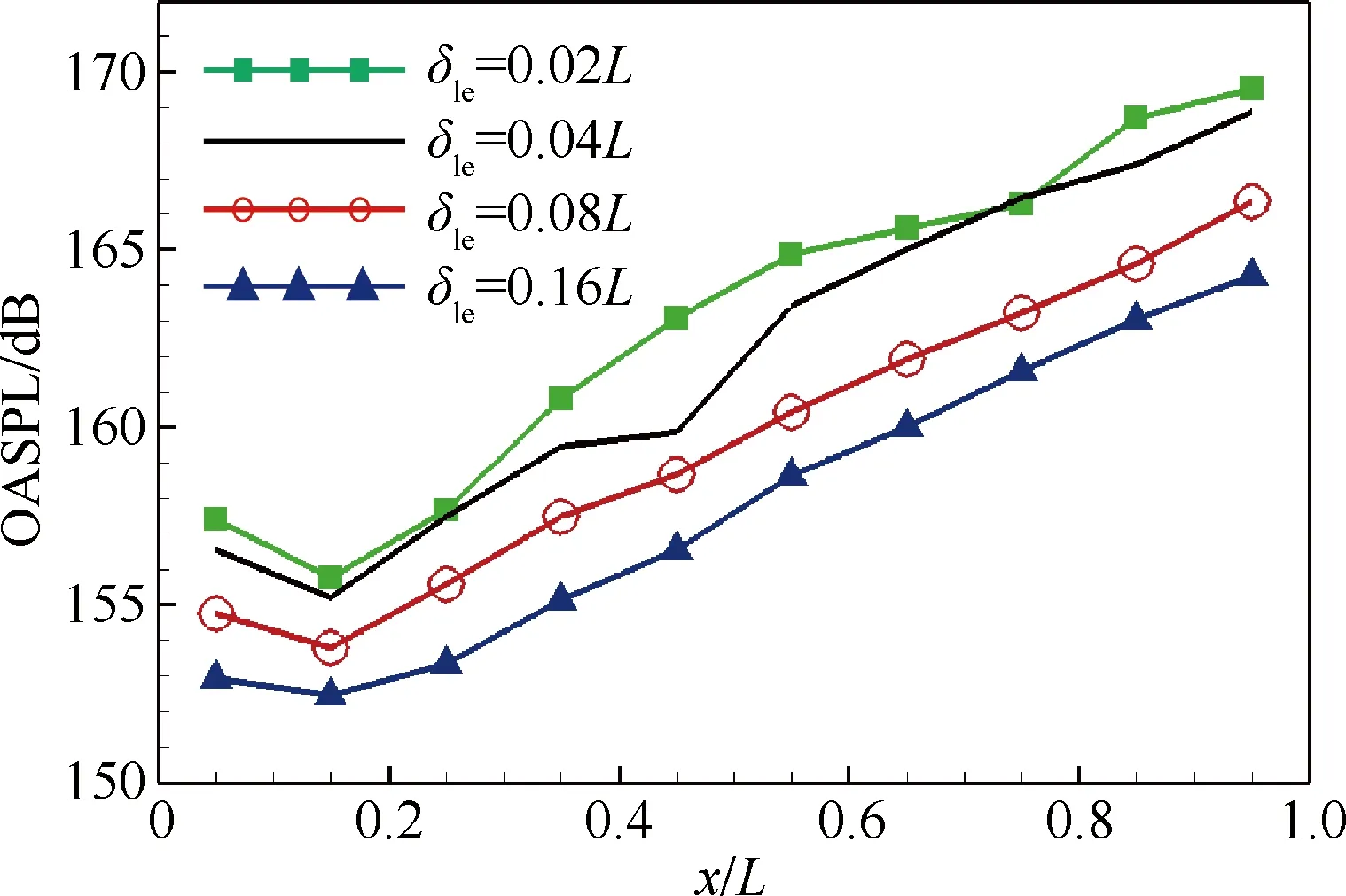
图8 空腔底部总声压级分布
Fig. 8 Distributions of OASPL at bottom of cavity
图9比较了K29位置脉动压力声压级(SPL)频谱,可看出,各工况的脉动压力频谱特性十分相似,低频部分由于流声耦合,出现了多个声压峰值频率(声模态频率),而高频区域表现为宽频随机噪声。随着边界层厚度增加,各阶声压峰值频率向低频方向偏移(见表1,表中数据与Rossiter的经验公式[30]结果进行对比,f=[(m-γ)/(Ma+1/K)](U/L)),而高频区域的宽频噪声也有所下降。K20~K28位置的脉动压力的声压级频谱曲线变化规律跟K29位置保持一致。低频区出现的声压峰值频率偏移主要与流声耦合回路的变化有关。观察图5可知,随着边界层厚度增加,自由剪切层厚度增加,同时剪切层向下游迁移的平均速度降低,使流声耦合周期延长,导致各阶声模态频率降低。

图9 脉动压力功率谱密度对比(K29)
Fig.9 Comparison of PSD of pressure fluctuations (K29)

表1 声模态频率对比
4.4 对流动类型的影响
图10(a)~图10(d)展示了空腔中截面的流场结构,不同工况下,空腔的流场十分相似,腔内的主要流动结构是两个顺时针旋转的旋涡,其中靠近前缘的涡占据的面积较大,而尾缘涡较小。对于开式空腔流动类型(见图10(e)),分离线从前缘角点出发,横跨空腔,直接落到后缘角点附近。对于闭式流动类型(见图10(f)),分离线从前缘出发后逐渐下降到空腔底部,并一直附着在腔底部,快到腔后缘才开始抬升。本文计算得到的空腔流动中,分离线从前缘出发后开始下降,但没有碰到腔底部,快靠近腔后缘时又开始抬升,是一种介于开式流动和闭式流动之间的过渡式流动类型,可以看到随着边界层厚度增加,尾缘涡尺寸增大,从空腔前缘角点发出的分离线(红色虚线)位置也不断上升,最低点位置从0.14D增加到0.39D,说明空腔流动类型虽然仍保持在过渡式流动类型范围内,但是逐渐向开式流动类型方向转换。从图10可以看到,从前缘进入空腔的部分流体,在与后壁相碰后向下偏转,并穿过后/前缘涡与壁面的间隙,回流至空腔前壁。随着边界层厚度的增加,前、后缘漩涡的交点位置不断抬高,漩涡与壁面间流道面积增大,且沿流向变化也更均匀,壁面静压梯度随之降低。另一方面,观察压力分布曲线可以看到,δle为0.02L时,压力系数从空腔中部抬升一段距离后出现了回调,这是闭式流动的典型特征之一, 如图11所示[4],说明此时流动对应过渡/闭式流动类型;随着边界层厚度的增加,回调区逐渐演变为平台区,而且平台区的范围逐渐缩小,闭式流动特征逐渐消失。δle为0.16L时,平台区基本消失,其压力系数分布曲线与开式流动类型十分相似。空腔流场和压力系数分布的分析结果均表明,边界层厚度增加会促使流动类型往开式流动方向转换。
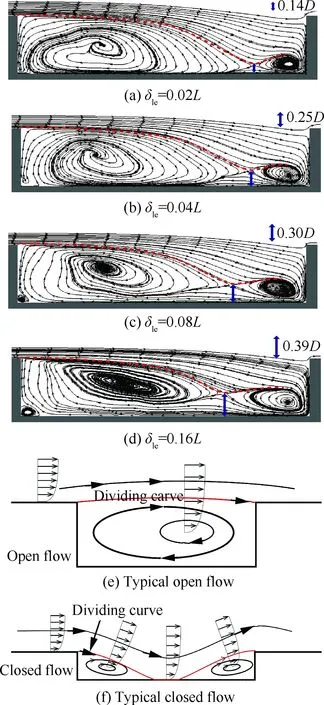
图10 空腔流动结构[3]
Fig.10 Cavity flow structures[3]
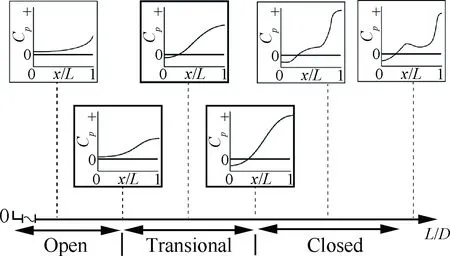
图11 基于流向压力系数分布的空腔流动分类[4]
Fig.11 Classification for cavity flows based on streamwise pressure coefficient distribution[4]
5 结 论
采用DDES方法研究了马赫数0.85条件下湍流边界层厚度变化对三维空腔非定常流动的影响。
1) 随着边界层厚度增大,其下游剪切层覆盖的范围增大,但是剪切层增长率降低。
2) 随着边界层厚度增加,空腔前后压差减小,同时腔内压力梯度下降。
3) 边界层厚度增加,空腔底部脉动压力声压级随之下降,同时各阶声压峰值频率向低频方向偏移。
4) 对于本文计算的过渡式空腔流动,边界层厚度增加会促使空腔流动类型往开式流动方向转换。
致 谢
感谢中国空气动力研究与发展中心高速空气动力研究所梁锦敏工程师在脉动压力数据处理方面提供的帮助。
[1] HUANG W, POURKASHANIAN M, MA L, et al. Investigation on the flameholding mechanisms in supersonic flows: Backward-facing step and cavity flameholder[J]. Journal of Visualization, 2011, 14(1): 63-74.
[2] XIAO L, XIAO Z, DUAN Z, et al. Improved-delayed-detached-eddy simulation of cavity-induced transition in hypersonic boundary layer[J]. International Journal of Heat and Fluid Flow, 2015, 51: 138-150.
[3] PLENTOVICH E B, STALLINGS R L, TRACY M B. Experimental cavity pressure measurements at subsonic and transonic speeds: Static-pressure results: NASA TP-3358[R]. Washington, D.C.: NASA, 1993.
[4] TRACY M B, PLENTOVICH E B. Cavity unsteady-pressure measurements at subsonic and transonic speeds: NASA TP-3669[R]. Washington, D.C.: NASA, 1997.
[5] STALLINGS R L, JR, WILCOX F J, JR. Experimental cavity pressure distributions at supersonic speeds: NASA TP-2683[R]. Washington, D.C.: NASA, 1987.
[6] PLENTOVICH E B. Three-dimensional cavity flow fields at subsonic and transonic speeds: NASA TM-4209[R]. Washington, D.C.: NASA, 1990.
[7] DE M J, HENSHAW C. M219 cavity case: Verification and validation data for computational unsteady aerodynamics: TR RTO-TR-26, AC/323 (AVT) TP/19[R]. 2000.
[8] 杨党国, 罗新福, 李建强, 等. 来流边界层厚度对开式空腔气动声学特性的影响分析[J]. 空气动力学学报, 2011, 29(4): 486-490. YANG D G, LUO X F, LI J Q, et al. Analysis of aeroacoustic characteristics in open cavities influenced by boundary-layer thickness[J]. Acta Aerodynamica Sinica, 2011, 29(4): 486-490 (in Chinese).
[9] 杨党国, 李建强, 范召林, 等. 超声速来流边界层厚度对浅腔声学特性的影响[J]. 航空动力学报, 2010, 25(4): 907-911. YANG D G, LI J Q, FAN Z L, et al. Shallow cavity noise influencing by boundary-layer thickness at supersonic speeds[J]. Journal of Aerospace Power, 2010, 25(4): 907-911 (in Chinese).
[10] 侯中喜, 易仕和, 王承尧. 超声速开式空腔流动的数值模拟[J]. 推进技术, 2001, 22(5): 400-403. HOU Z X, YI S H, WANG C Y. Numerical analysis of supersonic open cavity[J]. Journal of Propulsion Technology, 2001, 22(5): 400-403 (in Chinese).
[11] 张宝兵. 空腔流动的机理模拟和控制[D]. 南京: 南京航空航天大学, 2011. ZHANG B B. Numerical simulation and control of cavity flow[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2011 (in Chinese).
[12] LEVASSEUR V, SAGAUT P, MALLET M, et al. Unstructured large eddy simulation of the passive control of the flow in a weapon bay[J]. Journal of Fluids and Structures, 2008, 24(8): 1204-1215.
[13] RONA A, CHEN X X, ZHANG X, et al. Control of cavity flow scillation through leading edge flow modification: AIAA-1998-0672[R]. Reston: AIAA, 1998.
[14] 管德会, 蔡为民. 扰流板对内埋导弹偏航姿态角的影响[J]. 航空学报, 2014, 35(4): 942-947. GUAN D H, CAI W M. Spoiler’s effect on the yawing attitude angle of the missile in the bay[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(4): 942-947 (in Chinese).
[15] GLOERFELT X. “Cavity noise”, arts et metiers paristech, laboratoire de simulation numérique en mécaniques des fluides[EB/OL] (2009) [2015-03-06]. http://sin-web.paris.ensam.fr/squelettes/ref_biblio/Gloerfelt_VKI_2009a.pdf.
[16] CROOK S D, LAU T C W, KELSO R M. Three-dimensional flow within shallow, narrow cavities[J]. Journal of Fluid Mechanics, 2013, 735: 587-612.
[18] BASLEY J, PASTUR L R, LUSSEYRAN F, et al. On the modulating effect of three-dimensional instabilities in open cavity flows[J]. Journal of Fluid Mechanics, 2014, 759: 546-578.
[19] GAI S L, KLEINE H, NEELY A J. Supersonic flow over a shallow open rectangular cavity[J]. Journal of Aircraft, 2014, 52(2): 609-616.
[20] TUNA B A, ROCKWELL D. Self-sustained oscillations of shallow flow past sequential cavities[J]. Journal of Fluid Mechanics, 2014, 758: 655-685.
[22] HAASE W, BRAZA M, REVELL A. DESider—A European effort on hybrid RANS-LES modelling: Results of the European-Union Funded Project, 2004-2007[M]. Berlin: Springer Science & Business Media, 2009: 270-285.
[23] 司海青, 王同光. 边界条件对三维空腔流动振荡的影响[J]. 南京航空航天大学学报, 2006, 38(5): 595-599. SI H Q, WANG T G. Influence of boundary condition on 3-D cavity flow-induced oscillations[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2006, 38(5): 595-599 (in Chinese).
[24] ZHANG X, EDWARDS J A. Computational analysis of unsteady supersonic cavity flows driven by thick shear layers[J]. Aeronautical Journal, 1988, 92(119): 365-374.
[25] RONA A, DIEUDONNÉ W. Unsteady laminar and turbulent cavity flow models by second order upwind methods: AIAA-1999-0656[R]. Reston: AIAA, 1999.
[26] STANEK M J, VISBAL M R, RIZZETTA D P, et al. On a mechanism of stabilizing turbulent free shear layers in cavity flows[J]. Computers & Fluids, 2007, 36(10): 1621-1637.
[27] PENG S H. Simulation of turbulent flow past a rectangular open cavity using DES and unsteady RANS: AIAA-2006-2827[R]. Reston: AIAA, 2006.
[28] LAWSON S J, BARAKOS G N. Review of numerical simulations for high-speed, turbulent cavity flows[J]. Progress in Aerospace Sciences, 2011, 47(3): 186-216.
[29] VAKILI A D, GAUTHIER C. Control of cavity flow by upstream mass injection[J]. Journal of Aircraft, 1994, 31(1): 169-174.
[30] ROSSITER J E. Wind tunnel experiments on the flow over rectangular cavities at subsonic and transonic speeds[R]. Farnborough: Ministry of Aviation, Royal Aircraft Establishment, 1964.
刘俊 男, 硕士, 助理工程师。主要研究方向: 非定常流动数值计算。
Tel: 0816-2462114
E-mail: ljun05@163.com
杨党国 男, 博士, 副研究员。主要研究方向: 气动噪声。
Tel: 0816-2462114
E-mail: yangdg-cardc@163.com
王显圣 男, 博士, 助理研究员。主要研究方向: 流动稳定性。
Tel: 0816-2462114
E-mail: wxs2004@gmail.com
Received: 2015-03-06; Revised: 2015-03-31; Accepted: 2015-04-24; Published online: 2015-04-30 14:47
URL: www.cnki.net/KCMS/detail/11.1929.V.20150430.1447.001.html
Foundation items: National Basic Research Program of China (613240); State Key Laboratory of Aerodynamics Foundation (SKLA20140302)
*Corresponding author. Tel.: 0816-2462114 E-mail: ljun05@163.com
Effect of turbulent boundary layer thickness on a three-dimensional cavity flow
LIU Jun*, YANG Dangguo, WANG Xiansheng, LUO Xinfu
StateKeyLaboratoryofAerodynamics,ChinaAerodynamicsResearchandDevelopmentCenter,
Mianyang621000,China
Unsteady numerical computation of a three-dimensional cavity with different thicknesses of turbulent boundary layer (TTBL) is conducted using the detached eddy simulation (DES) modeling approach. The rectangular cavity has an aspect ratio of 5∶1∶1, the Mach number is 0.85 and Reynolds number is 13.47×106m-1. Four calculated TTBLs are at the ratio of 1∶2∶4∶8. The results show that TTBL has a significant effect on the evolution of free shear layer, cavity floor pressure distribution, pressure fluctuation and cavity flow type. With the increase of TTBL, the region covered by free shear layer becomes larger but TTBL grows more slowly; the pressure differential between leading edge and trailing edge drops down and pressure gradient along the cavity floor also decreases. Meanwhile, sound pressure level of pressure fluctuation reduces, peaks of tonal modes transfer to lower frequencies and the cavity flow tends to open flow type with thicker turbulent boundary layer.
detached eddy simulation; thickness of turbulent boundary layer; three-dimensional cavity; unsteady flow; flow type
2015-03-06;退修日期:2015-03-31;录用日期:2015-04-24; < class="emphasis_bold">网络出版时间:
时间: 2015-04-30 14:47
www.cnki.net/KCMS/detail/11.1929.V.20150430.1447.001.html
国家“973”计划 (613240); 空气动力学国家重点实验室研究基金 (SKLA20140302)
.Tel.: 0816-2462114 E-mail: ljun05@163.com
刘俊, 杨党国, 王显圣, 等. 湍流边界层厚度对三维空腔流动的影响[J]. 航空学报, 2016, 37(2): 475-483. LIU J, YANG D G, WANG X S, et al. Effect of turbulent boundary layer thickness on a three-dimensional cavity flow[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(2): 475-483.
http://hkxb.buaa.edu.cn hkxb@buaa.edu.cn
10.7527/S1000-6893.2015.0112
V211; TB84
: A
: 1000-6893(2016)02-0475-09
*
