低轨卫星多普勒频移特性几何估计算法
2016-02-22王爱华王星原陈丽婷
王爱华, 王星原, 陈丽婷
(北京理工大学 信息与电子学院,北京 100081)
低轨卫星多普勒频移特性几何估计算法
王爱华, 王星原, 陈丽婷
(北京理工大学 信息与电子学院,北京 100081)
为了能实时准确地计算低轨卫星的多普勒频移,提出了一种适用于不同偏心率的低轨道卫星多普勒频移几何计算方法. 该方法无需地面终端经纬度位置及卫星实时坐标,仅由卫星轨道参数及终端处最大可视仰角即可得到当前可见窗内多普勒频移特性. 算法计算过程简单、复杂度低、利于片上编程,仿真结果及数值分析均表明该算法具有较高的精确度,可为卫星通信接收机多普勒频移估计与补偿提供先验信息.
低轨卫星;多普勒频移时变特性;不同轨道偏心率
低轨(LEO)卫星的轨道高度低,信号的传播路径短、损耗低、时延小,是当今卫星移动通信系统的重要组成部分. 但另一方面,卫星轨道高度低、运行速度快,也使得信号在传输过程中会产生十分可观的多普勒频移,而多普勒频移的快速时变特性使得卫星移动通信的信道特性变得更加复杂,快速准确地预测多普勒频移时变特性变得至关重要.
文献[1-2]是基于两行轨道根数(TLE)的SGP4/SDP4模型,该模型目前被广泛应用于高精度轨道预测;文献[3]是基于卫星星历与航天轨道运动学的轨道预测算法. 此两种算法均可精确计算卫星与地面终端的相对位置和速度,再通过空间坐标矢量运算,便可以高精度地预估任意轨道卫星与地面站之间的多普勒频移. 但因其算法运用了大量乘法运算、矩阵运算,算法的复杂度高,并且需要大量的数据存储空间,故不适用于资源受限的应用平台,如片上仿真平台. 文献[4-6]利用球面几何计算出多普勒频移曲线,该方法较为简单,计算量小,但只适用于圆形轨道,不具有普适性. 本文在文献[4]的基础上,考虑了轨道偏心率对多普勒频移的影响,提出了一种适用于椭圆轨道与圆形轨道的多普勒频移快速计算方法,并且对该算法的性能进行了分析验证.
1 多普勒频率计算
在地球地心固定坐标系(ECF)中,将地球视为一个平均半径Re=6 370 km的圆球,地面观测站E、卫星运行轨道以及卫星星下点轨迹的几何关系如图1、图2所示.
A点为卫星在仰角最大时刻t0时的星下点,B点为任意时刻t的星下点.θ(t)为任意时刻卫星可见仰角,∠EOB=α(t)为任意时刻卫星与地面观测站对应于地心的角距,在最大仰角时刻,∠EOA=α(t0),∠AOB=β(t)为A点与B点的角距.
在实际观测中,低轨卫星的可视时间远远小于卫星周期,因此可以忽略地球自转的影响,将可视窗下的星下点轨迹近似为大圆[4]. ΔEAB即为地球大圆上的球面三角形,其中∠EAB=90°.
文献[4]中为了简化分析和计算,假定卫星轨道为圆形轨道,即任意时刻t卫星S到地心O的距离为定值r,依据几何关系得到地面观测站E点的归一化多普勒频移为[4]
(1)
式中:令ωF(t)≈ωs-ωecos(i),ωs为卫星运动平均角速度,ωe为地球自转角速度;i为卫星轨道倾角,在t0时刻仰角最大,为θmax.
但在实际情况中,大部分卫星轨道存在偏心率,不是圆形轨道. 针对此种情况本文提出了适用于不同轨道偏心率的低轨卫星多普勒频率时变特性计算方法.
假设卫星轨道的长半轴为a,卫星轨道偏心率为e,根据开普勒定律,可知
式中:μ为地球引力常数,μ=GM=3.986 005×1014m3/s2[7].
为了简化计算,假设卫星在轨道上运动只受到地球引力场的影响[7]. 若已知t0时刻的平近点角为M0,则任意时刻t的平近点角
(2)
已知卫星轨道偏心率e,则偏近点角E(t)满足关系式
(3)
真近点角f(t)可由偏心率e和偏近点角E(t)表示为
(4)
任意时刻t卫星S到地心O的距离r(t)为
(5)
t0时刻θ(t0)=θmax,可得此时卫星与地面站的距离s(t0)为
(6)
如图2所示,在球面直角三角形ΔEAB中有如下三角函数关系
(7)
式中:
(8)
在地心惯性系(ECI)中,∠SOS′=f(t)-f(t0),但在ECF中,计算星下点的角距∠AOB必须考虑地球自转的影响[4],故令
式中ωe为地球自转角速度,ωe=7.292 115×10-5rad/s.
由图1可知,在ΔSOE中,卫星与地面站的距离s(t)为
(9)
即
(10)
由此可以得到归一化多普勒频移
式中:c为光速,c=3×108m/s,ds(t)/dt为地面站与卫星的径向速度.
令θmin为最小可见仰角,即当θ(t)≥θmin时,卫星对于地面观测站E可见. 由
(11)
可算出可视窗的大小,θmin的大小受地面站周围环境的影响,且地势越平坦,θmin越小. 为了在最大限度的可视窗内观测卫星的运动,本文令θmin=0.
2 仿真结果及性能分析
2.1 算法仿真及精确度分析
为了验证本算法对于不同偏心率轨道卫星的适用性,选取目前在轨运行[8]的4颗偏心率不同的卫星,仿真参数如表1所示,令最大仰角时刻t0=0.
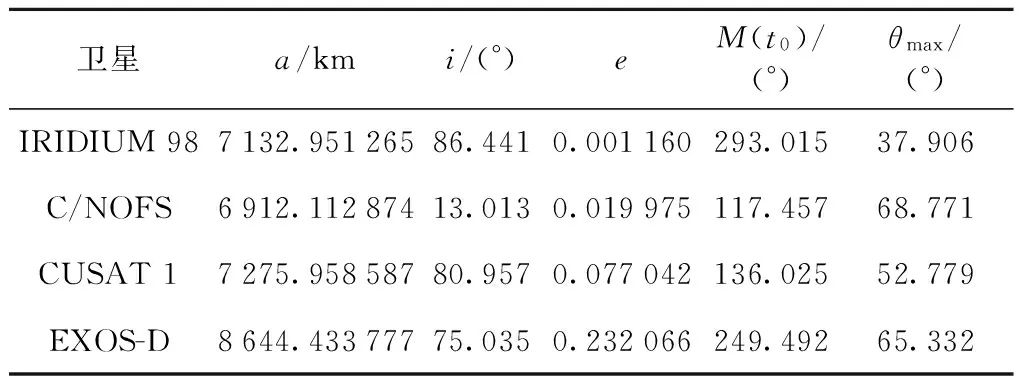
表1 仿真参数
图3给出了4颗具有不同轨道参数卫星的归一化多普勒频移时变特性仿真曲线. 其中STK曲线是STK(satellite tool kit)软件生成的基于SGP4/SDP4模型的多普勒频移曲线,STK软件能高精度模拟卫星轨道,在本文中以它作为精度评价的参考. Sim1是基于文献[4]中的圆形轨道多普勒频移计算方法计算得到的仿真曲线;Sim2为本文算法仿真曲线. 从图3中可以看出,Sim1在近圆轨道下与STK有较好的契合度;Sim2在偏心率不同的卫星轨道下,均能很好地吻合STK曲线.
多普勒频移均方误差值(MSE).为
(12)
表2为在载波频率fc=2 GHz条件下,由式(12)得出的多普勒频移均方误差值,可以看出,在4种不同的轨道参数下,本文算法的MSE均小于圆轨道算法.

表2 多普勒频移均方误差值(fc=2 GHz)
2.2 算法复杂度分析
一个算法的运行时间将直接制约着系统的性能,本节在Matlab环境下对以下两种算法不同运算间隔的运行时间进行模拟:算法1是基于SGP4/SDP4模型的多普勒预测算法,为上文中STK软件所使用的算法;算法2是本文所提出算法. 两种算法在其他外界环境以及精度要求一致的条件下,对卫星某一可见窗内的多普勒频移特性进行仿真计算,Matlab仿真得出基于SGP4模型的算法计算时间tg以及本文算法的计算时间ts,如表3所示.
从表3中可以看出,两种算法的计算时间均随着可见窗内时间分辨率的提高而增加,但本文算法的绝对运行时间要远小于SGP4/SDP4模型的多普勒预测算法. 此外,从二者的比值可以看出,前者算法的运算时间对分辨率的提升更为敏感,而本文算法的时间增长幅度要远小于前者.
表3 不同分辨率下两种算法的时间复杂度
Tab.3 Time complexity of two algorithms with different resolution
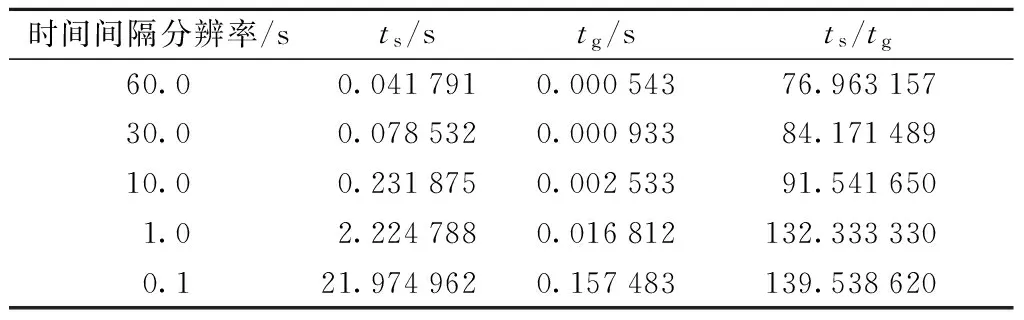
时间间隔分辨率/sts/stg/sts/tg60.00.0417910.00054376.96315730.00.0785320.00093384.17148910.00.2318750.00253391.5416501.02.2247880.016812132.3333300.121.9749620.157483139.538620
3 结 论
本文在文献[4]的基础上,结合二体模型理论,提出了一种适用于不同偏心率近地轨道卫星的多普勒频移几何计算方法. 该方法在卫星轨道根数确定的条件下,地面站观测到的多普勒频移时变曲线仅与其最大可见仰角θmax相关. 经仿真及数值分析验证,此方法在不同轨道形状条件下均具有较高的精确度,其算法时间复杂度近乎为基于SGP4/SDP4模型多普勒预测算法的1%,运算简单,资源占用少,利于片上编程,因此该算法可以在资源受限的条件下进行低轨卫星多普勒频移仿真估计,具有较大应用价值.
[1] Kelso T S, Hoots F, Roehrich R. Spacetrack report No.3: models for propagation of NORAD element sets[R]. [S.l.]: AIAA,1988.
[2] Vallado D A, Crawford P, Hujsak R, et al. Revisiting spacetrack report# 3[J]∥AIAA-AAS Astrodynamics Specialist Conference and Exhibit, Guidance, Navigation and Control and Co-located Confererces. [S.l.]: AIAA, 2006-6753.
[3] Amiri S, Mehdipour M. Accurate Doppler frequency shift estimation for any satellite orbit[C]∥Proceedings of the 3rd International Conference on Recent Advances in Space Technologies, 2007(RAST'07).[S.l.]: IEEE, 2007:602-607.
[4] Ali I, Al-Dhahir N, Hershey J E. Doppler characterization for LEO satellites[J]. Communications, IEEE Transactions on, 1998,46(3):309-313.
[5] You M H, Lee S P, Han Y. Adaptive compensation method using the prediction algorithm for the Doppler frequency shift in the LEO mobile satellite communi-cation system[J]. ETRI Journal, 2000,22(4):32-39.
[6] 韩力,吴向春,罗伟雄.非静止轨道卫星信道多普勒频移特性[J].北京理工大学学报,2005,25(2):143-146.
Han Li, Wu Xiangchun, Luo Weixiong. Doppler shift characterization for Non-GEO satellite channels[J]. Journal of Beijing Institute of Technology, 2005,25(2):143-146. (in Chinese)
[7] 张更新,张杭.卫星移动通信系统[M].北京:人民邮电出版社,2001:35-48.
Zhang Gengxin, Zhang Hang. Satellite mobile communication system[M]. Beijing: The People’s Posts and Telecommunications Press, 2001:35-48. (in Chinese)
[8] Celestrak. NORAD two-line element sets current data[EB/OL].[2014-02-17].http:∥celestrak.com/NORAD/elements.
(责任编辑:李兵)
A Geometric Algorithm of Doppler-Time Characterization for LEO Satellite
WANG Ai-hua, WANG Xing-yuan, CHEN Li-ting
(School of Information and Electronics, Beijing Institute of Technology, Beijing 100081, China)
To estimate Doppler frequency shift (DFS) accurately and rapidly, a geometric algorithm of LEO Doppler-time was provided to adapt to different eccentricity. Based on the orbital parameters and the maximum visual elevation angle, the algorithm can get the Doppler-time characterization during the satellite’s visibility window, which is irrelative to the terminal location and the satellite coordinate. Simulation results and numerical analysis indicate that the algorithm has higher precision, lower complexity and is easy for programming on-chip. And it can provide prior information for satellite communication receiver to estimate and compensate the Doppler frequency shift.
LEO satellite; Doppler-time characteristic; different eccentricity
2014-04-21
国家“八六三”计划项目(2012AA01A505);国家自然科学基金资助项目(61271258)
王爱华(1965—),女,博士,教授,E-mail:wah@bit.edu.cn.
TN 927.2
A
1001-0645(2016)12-1294-04
10.15918/j.tbit1001-0645.2016.12.016
