低代价的数据流分类算法①
2016-02-20李南
李 南
(福建农林大学 计算机与信息学院, 福州 350002)
低代价的数据流分类算法①
李 南
(福建农林大学 计算机与信息学院, 福州 350002)
现有数据流分类算法大多使用有监督学习, 而标记高速数据流上的样本需要很大的代价, 因此缺乏实用性. 针对以上问题, 提出了一种低代价的数据流分类算法2SDC. 新算法利用少量已标记类别的样本和大量未标记样本来训练和更新分类模型, 并且动态监测数据流上可能发生的概念漂移. 真实数据流上的实验表明, 2SDC算法不仅具有和当前有监督学习分类算法相当的分类精度, 并且能够自适应数据流上的概念漂移.
概念漂移; 数据流; 分类; 低代价; 监督学习
数据流分类现已成为数据挖掘领域的一个研究热点, 涉及的实际应用包括网络入侵检测以及垃圾邮件过滤等. 数据流上的样本持续、快速地到来, 使得传统的一次性静态学习的数据挖掘算法无法适用. 此外,数据流上隐含的知识也有可能随着时间的推移而发生变化, 出现概念漂移[1]现象. 例如, 某些特定商品(如冷饮)的销量随着季节会呈现周期性的变化, 大家在网上关注的热点话题会不断变化等. 如何捕获数据流上的当前概念也为处理数据流分类问题带来了新的挑战.
目前对数据流进行分类, 单一分类模型和集成分类模型是学者们主要采用的两种方式. 单一分类模型首先在训练样本集合上建立初始分类模型, 然后为了拟合当前数据流样本的分布情况, 用随后到来的样本对现有模型进行增量式更新. 然而, 这种模型通常结构复杂, 并且需要频繁地对模型进行繁琐的更新. 在将数据流上的样本按照到来的时间划分为大小相同的数据块后, 集成分类模型用新数据块上建立的基分类器, 替换当前模型中分类性能较差或者已经过时的基分类器. 由于基分类器的训练速度通常比单一模型的更新速度快[2], 因此集成分类模型更适合对高速持续产生的数据流进行分类.
本文提出一种采用集成分类模型方式的低代价的数据流分类算法(Semi-supervised learning algorithm for Stream Data Classification, 简称2SDC). 无论是采用单一分类模型还是集成分类模型, 现有绝大部分数据流上的分类算法重点只关注模型的分类效果, 进而假设所有待分类样本一旦被分类其类别信息即可立刻获得,然后马上利用这些类别信息对模型进行更新以最大限度地提高模型的分类精度, 这无疑人为忽略了标记数据流上样本所需的高昂代价. 本文的创新主要在于采用半监督学习的思想来降低更新现有模型所需要的有类别标记样本的使用量, 因此更符合实际应用中的要求. 此外, 算法主动检测概念漂移的发生, 这也加快了算法对数据流上当前概念的适应速度.
1 2SDC算法基分类器
现有绝大部分数据流上的分类算法使用全部样本的真实类别来拟合样本的当前分布情况, 而标记高速数据流上的所有样本需要很高的代价. 为了减少拟合数据当前分布所需要样本的数量, 2SDC算法首先使用类似于半监督学习的聚类算法, 将给定数据块划分为若干个簇. 然后, 挑选中其中有代表性的簇, 保存每个簇的中心、半径、所在子空间以及相应的类别作为集成分类模型的基分类器, 进而用其来拟合数据流上当前样本的分布情况.
1.1 无监督学习的K-means聚类算法
设固定大小的数据块D由N条样本组成, 即D={(x1,y1),(x2,y2),...,(xN,yN)}. 其中,xn=(xn1,xn2,...,xnM)表示由M维属性构成的第n条样本,yn∈{0,1,2,...,L}表示xn的类别. 如果yn=0, 表示该样本的类别未被标记.
要将数据块D中的样本划分为K个簇{C1,C2,...,C K}, 无监督的K-means聚类算法的目标是最小化所有样本到各自簇中心的距离之和, 即最小化目标函数:其中,ck表示第k个簇的中心,dis(x,ck)表示样本x与ck的相异度.
1.2 2SDC算法基分类器构建
为了降低标记样本所需要的代价, 训练集中应该只有少部分样本已标记类别. 此时, 聚类的目标应是在最小化所有样本到各自簇中心的距离之和的同时,使得已标记类别的来自同一类的样本尽可能的在相同的簇中, 即最小化目标函数:

公式(1)中的impk表示第k个簇的“不纯净”程度,算法中使用信息熵来衡量, 即表示第k个簇中属于第l类样本的先验概率, 即其中表示被划分到第k个簇的样本个数, |Ck(l)|表示Ck中属于第l类的样本个数. 显然, 如果被划分到Ck中的已标记类别的样本均来自同一个类, 那么impk=0, 此时impk最小. 相反, 若第k个簇中的已标记样本均匀地来自各个类别, 那么impk=log(L), 此时impk最大.
公式(1)中的vk表示第k个簇的权值.为了平衡“簇间相异度”(公式(1)中的前半部分)和“簇内纯净度”(公式(1)中的后半部分)的影响,取综合以上考虑, 2SDC算法中使用的聚类算法的目标函数为:

这样, 给定样本x以及簇中心{c1,c2...,cK},当前条件下的最优聚类为:
① 如果x是未标记类别的样本,
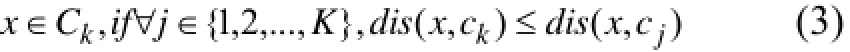
② 如果x是已标记类别的样本,

此外, 数据空间中往往存在与特定类别无关或者次要的属性[3]. 因此在聚类前, 需要先将样本投影到各个簇对应的子空间上, 然后再考虑其与各个簇中心的相异度. 这样也能减少聚类算法的迭代次数, 加快算法的收敛速度. 因此, 给定当前样本xi,xi和第k个簇的中心ck的相异度dis(xi,ck)应该采用加权的欧式距离来计算, 即算法中使用一个对角矩阵表示簇Ck中各个属性的权重(即所在的子空间), 其满足值得注意的是,即使是为来自同一类别的样本所建立的聚类, 也有可能在不同的子空间上. 以文本数据流分类为例, 来自“体育”类别的样本可能来自 “电子竞技”或者“传统项目”, 而这两个部分每个属性的权重显然应该是不一样的. 因此, 2SDC算法中为每个簇独立地设置一个属性权重.
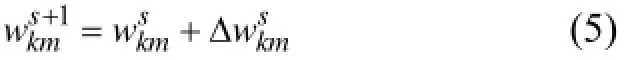
此外, 如果各个簇的初始中心是随机选取的, 这会对算法最终的结果造成较大的影响. 因此, 为了保证模型分类效果, 2SDC算法选取初始中心的方法为:设为每个类别样本建立的簇的个数为num(即选取K=num·L), 那么在数据块D中已标记的属于第l类的样本里, 依次选取num条最不相似的样本作为初始的簇中心. 综上所述, 2SDC算法基分类器构建过程如算法1.

?

Step3. 初始化迭代次数h=1. Step4. 根据公式(3)或公式(4), 依次将N条样本分配到各个簇中.h++. Step5. 更新每个簇的中心. Step6. 根据公式(5), 更新各个簇每个属性的权重. Step7. 如果≤ε-h+1ChC并且≤ε-h+1WhW,算法停止. 否则, 随机重新排列N条样本的顺序, 转向Step4. End
如果每次划分都只是将当前样本划分到当前最优的聚类中, 那么聚类结果和样本的排列顺序紧密相关.然而, 尝试所有的排列顺序以获得最优解是不现实的.因此算法1中在每次聚类后, 重新排列N条样本的顺序, 以接近最优解. 文献[4]中证明这种方式是收敛的.
在将数据块D划分为K个簇后, 2SDC算法将进行筛选, 选取其中有代表性的簇, 以四元组cluster={center,radius,weight,label} 的形式保存下来, 用来拟合D上各类别样本的分布情况. 其中,center表示cluster的中心,radius表示半径,weight表示所在的子空间,label表示类别. 具体过程如算法2.

Begin Step1. 在被划分到K个簇的已标记样本中, 依次选取各个类别标记样本最多的簇, 加入集合S. Step2. 在剩下的K-L个簇中, 删除已标记各类别样本之和过少(小于ε·labPer·N)的簇, 将剩下簇的加入S. Step3. 对于S中的簇, 构建相应的cluster. 其中,用xi表示簇Ck中距离中心最远的样本, 那么保存簇Ck的中心ck作为centerk, 属性权重Wk作为weightk,已标记类别样本里数量最多的类标签作为labelk,radiusk=dis(xi,centerk). End
2SDC算法基于普遍的聚类假设[5]: “属于同一聚类的样本很可能具有同样的类别”来对未知样本进行有效分类. 给定待分类样本x和一个基分类器Base,依次计算x和Base中所有cluster中心的加权距离. 如果(即x被覆盖), 那么根据聚类假设,x和建立clusterk的样本形成一个聚类,因此将x分类为labelk. 如果x被多个cluster覆盖, 那么选取其中类别数量最多的, 作为x类别的估计值.如果x不被任何cluster覆盖或者数量最多的类别不是唯一的, 那么说明x是难处理样本,Base不对其进行判断.
1.3 集成分类器构造
2SDC算法集成分类器E由p个基分类器和一个仲裁分类器构成. 其中仲裁分类器使用增量朴素Bayes分类器. 给定待分类样本x, 分类过程如算法3.

算法3: 2SDC算法分类输 入: 集成分类模型E, 待分类样本x输 出: x类别的估计值yBegin Step1. 依次使用基分类器对x进行分类. Step2. 设各基分类器对x类别的估计值分别为} ,..., {y1,y2yp Y=. 如果Y中出现次数最多的类别不唯一, 或者各基分类器均不对x进行判断, 那么使用仲裁分类器对x进行分类. 否则, 返回Y中出现次数最多的类别. End
每当新的数据块到来, 首先利用算法3, 使用现有分类模型E对样本进行分类. 然后, 训练一个新的基分类器. 如果E中现有的基分类器个数不超过p, 那么保存新的基分类器. 否则, 将原来基分类器中建立时间最早的替换出来. 最后, 用新数据块上的有标记类别的样本对仲裁分类器进行增量更新. 这样, 2SDC算法具有对cluster覆盖的样本高分类精度的同时, 对不被任何cluster覆盖的样本的分类精度也有了保证.
2 概念漂移检测
现有集成分类算法大多没有概念漂移检测机制,被动的使用新基分类器逐步替换过时基分类器的方式来适应概念漂移, 这会导致概念漂移发生后需要较长时间才能将过时的基分类器全部替换, 表现为模型的分类精度会出现较长时间的持续下降. 2SDC算法采用概念漂移检测机制, 当检测到概念漂移发生时, 立刻抛弃现有整个已经过时的集成分类模型, 因此能够更快地适应数据流上的最新概念.
文献[6]认为概念漂移产生的来源于样本与其类别的联合概率随着时间或者环境的改变而发生变化. 无论是某类的先验概率发生变化、某类的类概率发生变化还是样本后验概率发生变化, 都会导致已经稳定的现有模型的分类精度出现较大范围的波动. 即当数据流保持稳定时, 分类模型对于有标记类别样本的分类精度应该保持在一个比较稳定的水平. 因此, 2SDC算法使用一个高斯分布来拟合分类精度的分布情况. 设前t个数据块上有标记样本的平均分类精度为μ, 方差为σ. 如果t+1个数据块上有标记样本的分类精度低于μ-1.96σ, 那么说明出现概念漂移, 需要删除当前的基分类器和仲裁分类器, 重建分类模型以适应数据流上的现有概率. 此外, 数据流上不可避免的新类别样本的出现也是一种特殊的概念漂移. 因此, 如果当前数据块上标记样本中出现新类别的样本, 那么同样也需要重建分类模型.
3 实验结果与分析
本节在真实的文本数据流上对2SDC算法的分类效果进行测试. 实验环境为Intel(R) Core i5 2.5GHz CPU、4G RAM PC机. 比较算法使用数据流上常用的对比算法(Streaming Ensemble Algorithm , 简称SEA)[7]、比较具有代表性的加权集成分类算法(Aggregate Ensemble, 简称AE)[8]、基于决策树和Bayes混合模型的集成分类算法(Weight Ensemble Classifier -Decision Tree and Bayes, 简称WE-DTB)[9]以及基于半监督学习的数据流集成分类算法(Semi-Supervised Learning Based Ensemble Classifier, 简称SEClass)[10].值得注意的是, 前三种对比算法使用的所有样本均是有类别标记的, 而SEClass算法和2SDC算法使用的样本是部分标记类别的, 其中有标记类别的样本占所有样本数量的20%. 各种算法的参数分别参照对应文献中的设置, 数据块大小500, 2SDC算法中基分类器个数为5, 为各类样本保存的簇个数为3.
实验中使用的文本数据流来自20-Newsgroups数据集. 数据集的属性个数为500, 类别数为6, 样本的分布情况见表1. 实验中将数据集划分为两个部分来模拟数据流多类别出现概念漂移的情况. 在前半部分,只有来自med, baseball, autos, motor四个类别的样本;在后半部分中, motor类的样本消失, 并新出现了space和politics类的样本. 各种算法在20-Newsgroups数据集上的平均分类精度如表2所示. 由于2SDC算法基分类器初始中心选择的不同会对分类结果造成影响,因此结果采用10次实验的平均值, 并且在表2中给出方差.

表1 20-Newsgroups中各类分布

表2 各种算法在文本数据流上的平均分类精度
从表2中可以看出, 只使用少量有类别标记样本的2SDC算法分类效果优于使用全部有标记样本的WE-DTB算法和SEA算法, 达到和AE算法相当的水平, 并且优于基于半监督学习的SEClass算法. 虽然2SDC算法初始中心的不同会对分类结果造成一定的影响, 但是方差并不太大. 由于AE算法使用的所有样本都是有类别的, 而且算法在当前数据块上使用多种分类算法建立相应的多个分类器以构成集成分类模型,因此分类精度是所有算法中最高的. 为了检测本文使用的概念漂移机制的有效性, 不同算法在测试数据集上每连续500条样本的分类精度如图1所示.

图1 20-Newsgroups上分类精度比较
从图1可以很清晰的看出, 在某一时刻, 由于新类别样本的出现以及原来类别样本的消失, 各种算法的精度均出现了不同程度的下降. 随着新类别样本的不断出现, 在一定时间后, 分类精度又都逐渐恢复到了之前的水平. 本文提出的2SDC算法的恢复速度较快, 这也证实了本文使用的概念漂移检测机制的有效性. 此外, 不同标记比例下算法的平均分类精度见图2.

图2 不同标记比例下平均分类精度
从图2中可以看出, 随着有标记类别样本数量的增多, 基分类器的边界更加准确, 也有更多的样本参与到仲裁分类器的更新, 因此2SDC算法的分类精度逐渐增高. 当标记样本比例较低时, 模型的分类精度还是稳定在一个相当的水平. 不同类别样本保存的簇个数下算法的平均分类精度见图3.
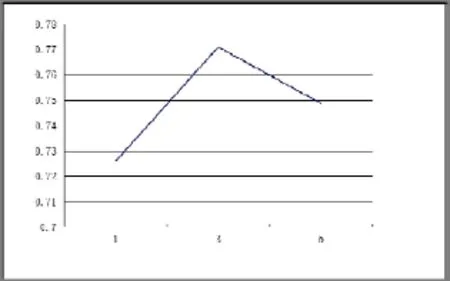
图3 不同簇个数下平均分类精度比较
从图3可以看出, 当为每个类别样本保存3个簇时, 分类效果最佳. 当簇个数过低时, 基分类器无法准确拟合各类别样本的分布情况, 导致分类精度较低.然而, 过高的簇个数降低了分类模型的泛化能力, 同样会降低模型的分类效果.
3 结语
本文提出了一种低代价的数据流分类算法2SDC.区别于使用所有待分类样本的真实类别来更新分类模型的现有大部分数据流分类算法, 新算法使用半监督学习的思想, 利用数据块上大量的未标记类别的样本,通过动态调整权值, 为每个类别建立不同的簇来拟合各类别样本的分布情况. 仲裁分类器的引入也保证了难处理样本的分类效果. 概念漂移检测机制的使用能够使得分类模型更快地适应数据流上的当前概念. 真实数据流上的实验证明了该算法的有效性. 下一步的工作方向是研究如何让算法自动调整各类别的初始簇个数.
1 辛轶,郭躬德,陈黎飞,毕亚新.IKnnM-DHecoc:一种解决概念漂移问题的方法.计算机研究与发展,2011,48(4):592–601.
2 Turner K, Ghosh J. Error collection and error reduction in ensemble classifiers. Connenction Science, 1996, 18(3): 385–403.
3 Aggarwal CC, Procopiuc C, Wolf JL, et al. Fast algorithm for projected clustering. Proc. of the ACM-SIGMOD. New York. ACM Press. 1999. 61–71.
4 Masud MM, Woolam C, Gao J, et al. Facing the reality of data stream classification: coping with scarcity of labeled data. Knowledge and Information System, 2012, 33(1): 213–244.
5 Zhou D, Bosquet O, Lal T N. Learning with local and global consistency. Advances in Neural Information Processing Systems, 2003, 16(1): 321–328.
6 Keller JM, Hand D. The impact of changing populations on classifier performance. Proc. of the 5th International Conference on Knowledge Discovery and Data Mining. New York. ACM Press. 1999. 367–371.
7 Street WN, Kim YS. A streaming ensemble algorithm (SEA) for large-scale classification. Proc. of the 7th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York. ACM Press. 2001. 377–382.
8 Zhang P, Zhu X, Shi Y, et al. An aggregate ensemble for mining concept drifting data streams with noise. Proc. of the 13th Pacific-Asia Conference on Knowledge Discovery. Bangkok. 2009. 1021–1029.
9 桂林,张玉红,胡学刚.一种基于混合集成方法的数据流概念漂移检测算法.计算机科学,2012,39(1):152–155.
10 徐文华,覃征,常扬.基于半监督学习的数据流集成分类算法.模式识别与人工智能,2012,25(2):292–299.
Low-Cost Algorithm for Stream Data Classification
LI Nan
(College of Computer and Information Science, Fujian Agriculture and Forestry University, Fuzhou 350002, China)
Existing classification algorithms for data stream are mainly based on supervised learning, while manual labeling instances arriving continuously at a high speed requires much effort. A low-cost learning algorithm for stream data classification named 2SDC is proposed to solve the problem mentioned above. With few labeled instances and a large number of unlabeled instances, 2SDC trains the classification model and then updates it. The proposed algorithm can also detect the potential concept drift of the data stream and adjust the classification model to the current concept. Experimental results show that the accuracy of 2SDC is comparable to that of state-of-the-art supervised algorithm.
concept drift; data stream; classification; low-cost; supervised learning
福建省自然科学基金(2013J01216,2016J01280)
2016-03-29;收到修改稿时间:2016-06-01
10.15888/j.cnki.csa.005556
