薄壁零件结构改进与性能优化

李少海

(西京学院机械工程学院，陕西 西安 710123)

薄壁零件结构改进与性能优化

李少海

(西京学院机械工程学院，陕西 西安 710123)

采用CAD/CAE技术研究薄壁箱式零件结构及其动力学性能。以某薄壁零件为研究对象，在WorkBench平台上创建了有限元模型，计算和分析了该零件的低阶自振频率及振型。建立了4种针对薄壁零件动态特性改进的结构设计方案，通过动力学参数计算与分析确定了一种最佳的薄壁零件结构形式。结果表明：采用十字筋结构可以有效增强薄壁零件的抗振性能，有利于机械设备的减振降噪及高速化运行。为薄壁零件的结构设计与动力学优化提供了重要技术参考。

薄壁零件；自振频率；筋结构；动力学

随着新型装备制造业的快速发展，高速化、智能化和集成化已成为现代食品加工机械的主要特点。薄壁箱式零件是食品加工机械中常见的一类结构，如榨油机的传动系统箱体、原料粉碎机及筛选机的振动箱体等。大多数食品机械是具有复杂机电系统构成的精密加工设备，机器在工作过程中产生的惯性离心力、非连续激振力等，均会直接或间接地作用于薄壁箱式零件[1]，由此引发的振动和噪声会严重影响机械系统的稳定性和食品加工质量[2]，不利于食品机械的高速、高精化发展；此外，薄壁箱式零件在食品机械设备中占有较大比重，其结构性能往往直接影响着食品加工过程的可靠性，因此有必要深入研究薄壁箱式零件的结构形式及其动力学性能。

1 薄壁零件结构

薄壁零件是高速加工机械设备中常用的支承部件，其结构多采用中空薄壁形式，图1(a)为某原料粉碎机的薄壁零件，主要由薄壁、底板、滑轨及内外加强筋构成，其中，滑轨主要用于支承主轴箱的上下往复运动，而驱动主轴箱运动的重锤及相关传动部分则安装于薄壁箱式零件内部[3]。在WorkBench平台上建立该薄壁零件的实体模型见图1(b)，其中，薄壁和加强筋的设计厚度均为35 mm，各加强筋相对于薄壁零件几何中心面呈对称分布。

图1 薄壁零件结构设计

2 动态计算与分析

2.1 动力学基础

薄壁零件为连续实体结构。根据有限单元法和振动力学理论，可将具有无限自由度的实体近似等效为有限自由度的离散结构[3]，其无阻尼自由振动微分方程见式(1)。

(1)

式中：

[M]——质量矩阵；

[K]——刚度矩阵；

{x}——位移矢量；

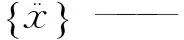
对于线弹性体结构，其自由振动可分解为一系列简谐运动，假设系统简谐运动方程为x=μsinωt，其中：μ为离散点振幅；ω为离散点振动圆频率。将其带入式(1)得到如式(2)所示的系统特征方程，其中ω2称为系统特征值[3]。由于薄壁零件振动时各离散点振幅不全为零，即式(2)中{μ}存在非零解，则其必须满足式(3)所示关系。

([K]-ω2[M]){μ}=0，

(2)

(3)

假设薄壁零件为n自由度系统，当[M]和[K]皆为正定矩阵时，求解式(3)可获得n个系统特征值ωr2(r=1,2,3,…,n)。对ωr2开方根可计算出系统各阶固有频率ωr，将其按大小进行排序：ω1<ω2<…<ωr<…ωn-1<ωn，其中ωr即该零件第r阶固有频率[4]。将系统各阶固有频率值带入式(2)，可计算出与之对应的各阶特征向量{μ}r={μr1,μr2,…,μrn}T，即薄壁零件的模态振型。

2.2 有限元模型

采用三维6面体20节点实体单元Solid186对薄壁零件进行结构离散，建立如图2所示的有限元模型，网格化后的模型包括6 222个单元和12 489个节点。零件材质选用吸振性强的灰铸铁，其力学性能参数见表1。考虑到计算效率和分析精度，建模过程对零件结构进行适当简化[4]，去掉影响不大的一些细节特征，如工艺孔、倒角等。

图2 有限元模型

材质密度/(kg·m-3)弹性模量/(N·m-2)泊松比灰铸铁72001.1×10-110.28

2.3 频率及振型

通过模态分析计算薄壁零件的自振频率和振型。图3为该零件1～15阶自振频率分布情况，其中前6阶为刚体模态频率(0 Hz)，从第7阶开始频率值逐渐依次增大。实际当中低阶频率对结构动力学性能影响较大，故在此只研究该薄壁零件的7、8、9阶自振频率，其频率值分别为52.16，70.96，95.81 Hz，其中基频为52.16 Hz，与之对应的安全工作转速在3 000 r/min左右。由于现代高速加工设备工作转速已高达数万转每分钟，例如日本精工早在2009年就已成功研制出了50 000 r/min的高速主轴部件，这对机体结构的动态性能提出了更高要求，所以为了提高生产效率和安全工作转速，图1所示的薄壁零件在动力学特性方面还有较大改进空间。

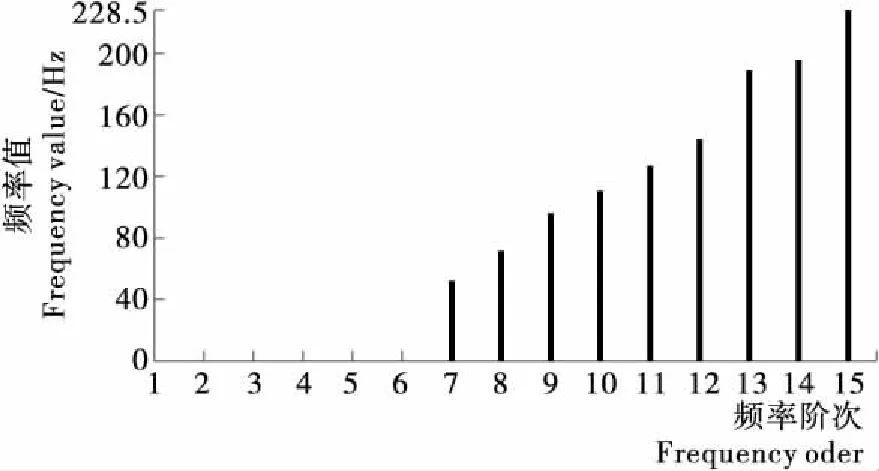
图3 自振频率分布图

图4 7～9阶振型

分析图4可知，该零件的7～9阶振动模式主要表现为薄壁的扭转或伸缩变形。第7、8阶振型均在零件顶部区域发生较大变形，其中，第7阶振型最大形变量约35.98 mm，出现在零件顶部边角位置；第8阶振型最大形变量约49.11 mm，出现在零件顶部加强筋与薄壁相交位置。第9阶振型最大形变出现在零件底部的加强筋边角区域，最大形变量约35.40 mm。根据自振频率与振动模式，能够有效预测和评估薄壁零件发生共振时的破坏趋势[5]，为食品加工机械的结构设计和工作转速控制提供了重要依据。

3 结构改进

根据结构动力学理论，结构的自振频率越高，其抗振性能越强，所以在进行减振设计时多以提高自振频率为目标。连续体结构的自振频率与其材质、刚度及质量密切相关，故在材质一定的条件下，可通过改进薄壁零件的形态来优化其动力学特性，如薄壁尺寸、加强筋数量及其布设形式等。

3.1 壁厚影响

考虑到质量对结构动态特性的影响，将零件的薄壁厚度分别增减5 mm，然后计算其自振频率和振型，见图5、6。分析可知，薄壁厚度增减5 mm后，第7阶与第9阶振型相似，均为薄壁结构的扭转振动变形，而第8阶振型的振动趋势则正好相反，即薄壁的内凹和外凸变形方向相反。此外，壁厚增加5 mm后，零件第7阶自振频率提高为59.14 Hz，而壁厚减小5 mm后，第7阶自振频率则降低至41.40 Hz，由此可见，在设计薄壁零件结构时，可通过增加壁厚来提高其自振频率。

图5 壁厚增加5 mm

图6 壁厚减小5 mm

3.2 加强筋形式

加强筋的布设形式决定了零件的结构刚度。在原有筋结构基础上改变其布设形式见图7，这两种筋结构均有助于改进薄壁零件的结构刚度，并且会对其动力学性能产生重要影响。

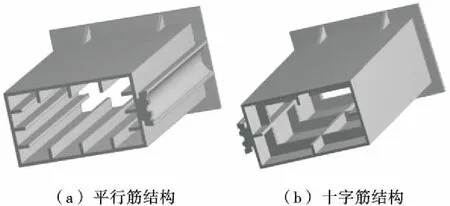
图7 筋结构布设形式

分别对两种筋结构下的薄壁零件进行自由模态分析，计算其自振频率及振型，见图8、9。分析可知，平行筋结构的第7阶自振频率仅为47.70 Hz，相比之下，十字筋结构的第7阶自振频率高达132.48 Hz，远远大于平行筋结构，说明十字筋结构下的薄壁零件具有更佳的动力学特性。除此之外，该零件在两种筋结构下的7～9阶振动模式也不尽相同，宏观上均表现为薄壁结构的扭转和伸缩振动，而且形变的趋势、振动幅值及分布区域也各不相同。

图8 平行筋结构

图9 十字筋结构

4 结果分析

不同设计方案下的薄壁零件动力学特性见图10、11。由图10、11可知，薄壁厚度和加强筋形式会对零件结构7～9阶自振频率产生明显影响，具体数据见表2。

图10 壁厚对频率影响

图11 筋结构对频率影响

阶次初始值壁厚+5mm壁厚-5mm平行筋结构十字筋结构752.1659.1441.4047.70132.48870.9680.1957.5666.49154.28995.81100.1089.7089.33166.79

分析表2可知，相对于初始结构，薄壁厚度减小5 mm和采用平行筋结构时该零件的第7～9阶自振频率会降低，说明这两种结构设计方案不利于改进薄壁零件的动力学性能；相比之下，将壁厚增加5 mm和采用十字筋结构时，薄壁零件的7～9阶自振频率则会明显增大，尤其是十字筋结构下的自振频率增幅更大，其第7阶自振频率相对于初始结构增大了80.32 Hz，由此可见，这种加强筋的布设形式能够有效增强薄壁零件的抗振性能，有利于机械系统的减振降噪与高速化运行。

5 结论

良好的动力学性能是现代食品加工机械系统高速、高精化发展的重要基础。通过薄壁零件结构的有限元建模、动态分析及改进设计，明确了不同结构形式对其动态特性的影响，同时获得了最佳的结构改进与动态优化方案，即采用十字筋结构时能够有效增强其抗振性能，为薄壁箱式零件的减振设计、结构改造及动力学性能优化提供了重要参考和依据，有利于食品加工机械的高速低振化设计。

[1] 管小清, 吕志强. 工业码垛机器人动力学仿真分析与研究[J]. 食品与机械, 2013, 29(1): 149-176.

[2] 陈小安, 刘俊峰, 合烨, 等. 高速电主轴热态性能及其影响[J]. 机械工程学报, 2013, 49(11): 135-142.

[3] 吕冬梅, 韩江. 大型数控双柱立车立柱动力学结构分析与优化[J]. 制造技术与机床, 2015(5): 42-45.

[4] 吴玲丽, 胡小秋, 赵雁. 加工中心立柱动态特性分析与比较[J]. 机械设计与制造, 2014(3): 117-119.

[5] 杨兆军, 陈传海, 陈菲, 等. 数控机床可靠性技术的研究进展[J]. 机械工程学报, 2013, 49(20): 131-139.

Structure improvement and performance optimization of thin-walled parts

LI Shao-hai

(College of Mechanical Engineering, Xijing University, Xi’an, Shaanxi 710123, China)

The CAD/CAE technical was used to study structure and dynamics characteristics of thin-walled parts. Based on a type of thin-walled part, its finite element model of was set up on WorkBench platform, and some low order natural frequency and vibration mode of its structure were also calculated and analyzed. Four structure design schemes about improving dynamic characteristics of the part was established, and then an optimal structure of it was determined through calculating and analyzing its dynamic parameter. The results indicated that vibration resistance of the part could be strengthened effectively by using the cross rib structure, and it was also advantageous to vibration noise reduction and high speed operation of machinery equipment as well. The study provided some important technical reference for structure design and dynamics optimization of thin-walled parts.

thin-wall parts; natural frequency; rib structure; dynamics

10.13652/j.issn.1003-5788.2016.12.021

西京学院科研基金项目(编号：XJ130236)

李少海(1981—)，男，西京学院讲师，硕士。 E-mail：254825567@qq.com

2016—04—25