船体纵骨上附连挺筋软踵形状参数优化

罗仁杰，邱伟强，蔡诗剑，陈 涛

（中国船舶及海洋工程设计研究院，上海 200011）

船体纵骨上附连挺筋软踵形状参数优化

罗仁杰，邱伟强，蔡诗剑，陈 涛

（中国船舶及海洋工程设计研究院，上海 200011）

船体纵骨上附连挺筋与纵骨面板连接处往往会因几何突变而出现应力集中现象，造成结构失效或损坏。对此，根据协调共同结构规范（HCSR）中图示推荐表和国内各大船厂的典型节点图册，选取3种工程中常用的软踵形式建立参数化模型，并利用Isight集成有限元建模软件Patran和计算软件Nastran进行形状参数优化计算，得到应力极值最小的软踵形状；同时，根据HCSR对3种最优的软踵形式进行疲劳强度校核，对比不同开孔形状下结构的疲劳寿命。计算结果表明，建议的优化流程能有效减小结构的应力峰值，提高节点疲劳寿命，得到不同船体位置处疲劳强度、屈服强度更优的软踵开孔形式及参数，有较强的工程实用价值，可应用到其他类似结构的节点设计中。

船舶、舰船工程；船体纵骨；软踵；PCL参数化建模；形状参数优化；疲劳强度

0 引 言

分析20世纪80年代至90年代期间日本建造的一批大型油船的外底纵骨和外板纵骨面板上出现大量裂纹损伤的原因，除了构件设计的尺寸余量相对规范要求较小之外，其中很重要的原因是：为简化建造工艺，纵骨上附连挺筋端部通焊孔的形状设计较为简单，挺筋端部未设置软趾和软踵，尤其是未设置软踵，造成普通纵骨挺筋软踵与纵骨面板相交处的应力过于集中；而且，也未经疲劳强度校核，导致纵骨及挺筋的疲劳强度（甚至是局部结构屈服强度）未能满足安全性要求，造成实船结构裂纹事故频发。

虽然软踵是否设置、软踵形状参数是否优化对于整船而言是一个很小的细节，但却是整船结构设计中普遍存在的典型结构“短板”，是造成船体纵骨承载能力下降的关键因素。

由于加强筋的软踵往往尺寸较小、对结构的整体承载能力影响不大，因此设计人员在结构设计过程中往往会忽略其形状参数设计，仅根据经验或规范采用常规的软踵形式和尺寸。然而，该类型和尺寸的软踵处往往会出现明显的应力集中现象，使得开孔边缘出现很高的应力点或应力区，长期的高应力作用会使结构出现屈服破坏或疲劳损坏，进而导致结构失效甚至破坏。因此，对加强筋的软踵形状进行优化设计，降低软踵自由边处的应力集中，有着重要的工程应用价值。

目前国内有关纵骨附连挺筋软踵形状参数优化的专业性文献较少，即使偶有涉及，所比较的样本数量也有限，得出的结论多为定性研究，在定量方面远未达到最优解。

这里所选的软踵形状方案来自于国内各大船厂的典型节点图册及协调共同结构规范（HCSR）第9章第4节的推荐形式，对纵骨附连挺筋软踵形状参数进行定性和定量的多方案、多参数及覆盖大多数工程实际节点形式的研究。最终采纳的方案不仅要满足节点的屈服强度要求、疲劳强度要求及纵骨与挺筋连接面积要求，而且要在工艺上更简化、在结构形式上更安全。

根据HCSR第9章第4节表4“应力集中因子”中给出的应力集中初值，仅设置软踵而不设置软趾的纵骨附连挺筋的疲劳强度性能优于既设置软踵又设置软趾的节点形式；同时，前者的材料利用率远高于后者，且适用于多数运输船的纵骨连接节点，深受广大船厂的欢迎。因此，这里仅对前者进行研究。

1 优化模型

以某油船双底、双壳纵骨与其附连挺筋的连接节点为例，选取3种工程中常用的纵骨挺筋软踵形式建立数学优化模型，并利用PCL（Patran Command Language）语言编写参数化建模程序，利用Isight集成通用有限元软件Patran和Nastran进行优化计算，得到不同位置处各软踵形式的最优开孔尺寸。选取的3种常用软踵形状见图1，模型的主要形状优化参数见图2。

根据HCSR第9章第4节表4“应力集中因子”中图形的示意，最优疲劳寿命的软踵形式ID2（见图3）的形状控制参数比图1中的软踵形式3略微复杂些。国内船厂目前的建造工艺水准尚难同时保证2个趾端的切割精度，大大增加了工厂切割和工艺误差控制的难度。此外，经过试算发现，规范中图示的软踵形式的屈服强度和疲劳强度相比图1中的软踵形式2和软踵形式3几乎没有优势，因此这里不作展开讨论。

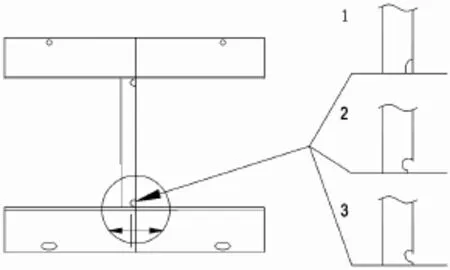
图1 3种常用的纵骨挺筋软踵形状

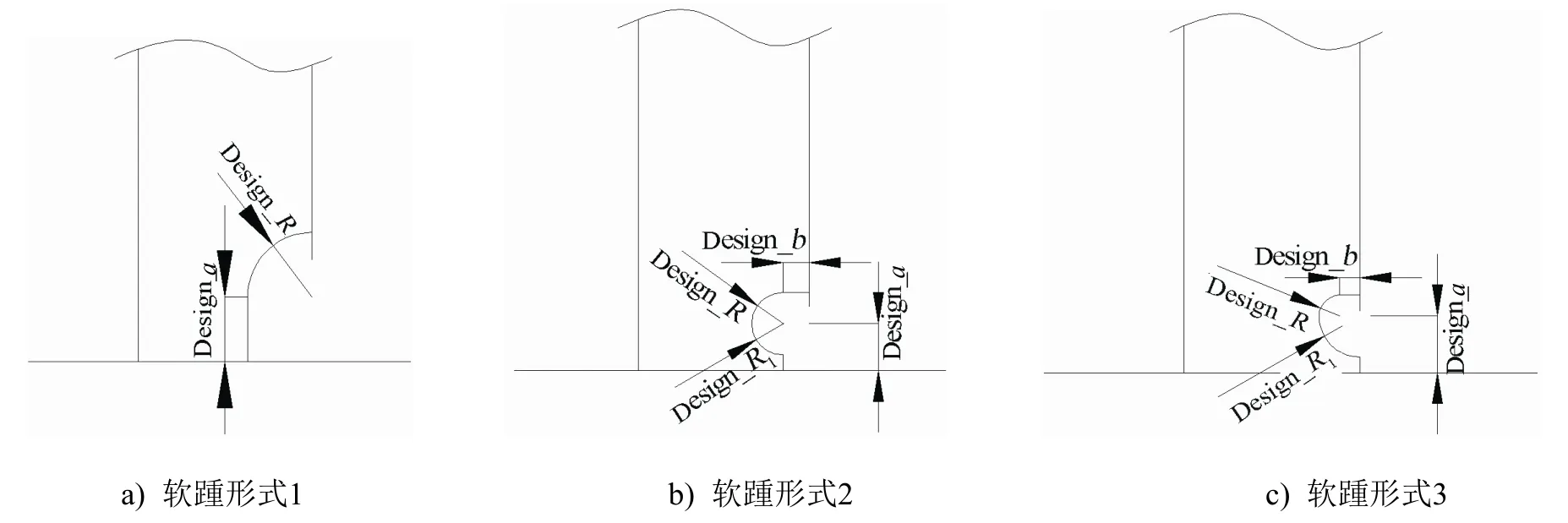
图2 纵骨挺筋软踵形状优化参数

优化目标函数是使软踵及其附近结构的屈服强度裕度最大，亦即求解使软踵开孔边缘附近合成应力相对最小、材料屈服极限裕度最大的开孔尺寸。建立的最优化数学模型见式(1)～式(3)，其中各软踵设计变量的上下限主要根据船厂的制造工艺和规范对软踵开孔尺寸的限制设置。

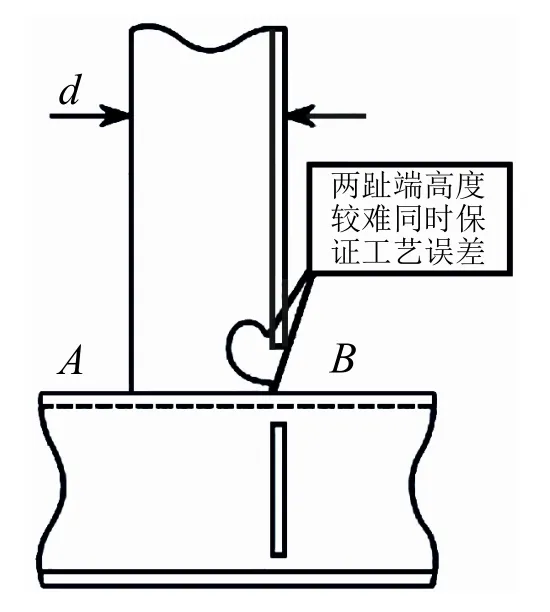
图3 HCSR第9章第4节表4纵骨端部连接形式ID2

式(3)中： F( X)为模型最大合成应力，采用有限元方法计算。

考虑到实际加工精度的限制，同时也为减少计算量，优化过程中所有变量均取整数，变化步长取为1。

2 lsight优化过程集成

利用Isight集成通用有限元软件Patran和Nastran进行纵骨挺筋软踵参数化建模及形状优化计算，其中需要利用有限元方法计算软踵开孔自由边的最大合成应力和正应力。

2.1 有限元模型

选取某油船双层底和舷侧3个位置的船体纵骨作为计算对象（见图4），各位置下的主要模型参数取值见表1，纵骨挺筋软踵的参数及初值取统一值（见表2）。船体强力纵向构件及纵骨的各形状和尺寸参数不作为本次优化的优化变量，而将软踵的各形状参数设置为优化变量，可在优化过程中依据优化算法进行迭代计算。

模型范围为：横向4个纵骨间距，纵向4个强框间距，垂向双壳高度/宽度。边界条件为：纵向一端取固定支撑边界，另一端纵向位移不约束，其他自由度约束；垂向在挺筋长度方向的另一端垂向位移约束，其他自由度不约束；横向边界节点采用对称边界条件。载荷包括带板上承受的均布载荷和横截面上所受的总纵弯曲应力；载荷大小根据规范要求，采用船级社规范计算软件进行计算。精细网格尺寸为t×t（t为板厚）。模型中材料均采用钢制材料，杨氏模量 E= 206000MPa ，泊松比 μ= 0.3，密度 ρ= 7850 kg/m3。整体参数化模型见图5。

图4 优化纵骨所在位置（矩形框所在位置）

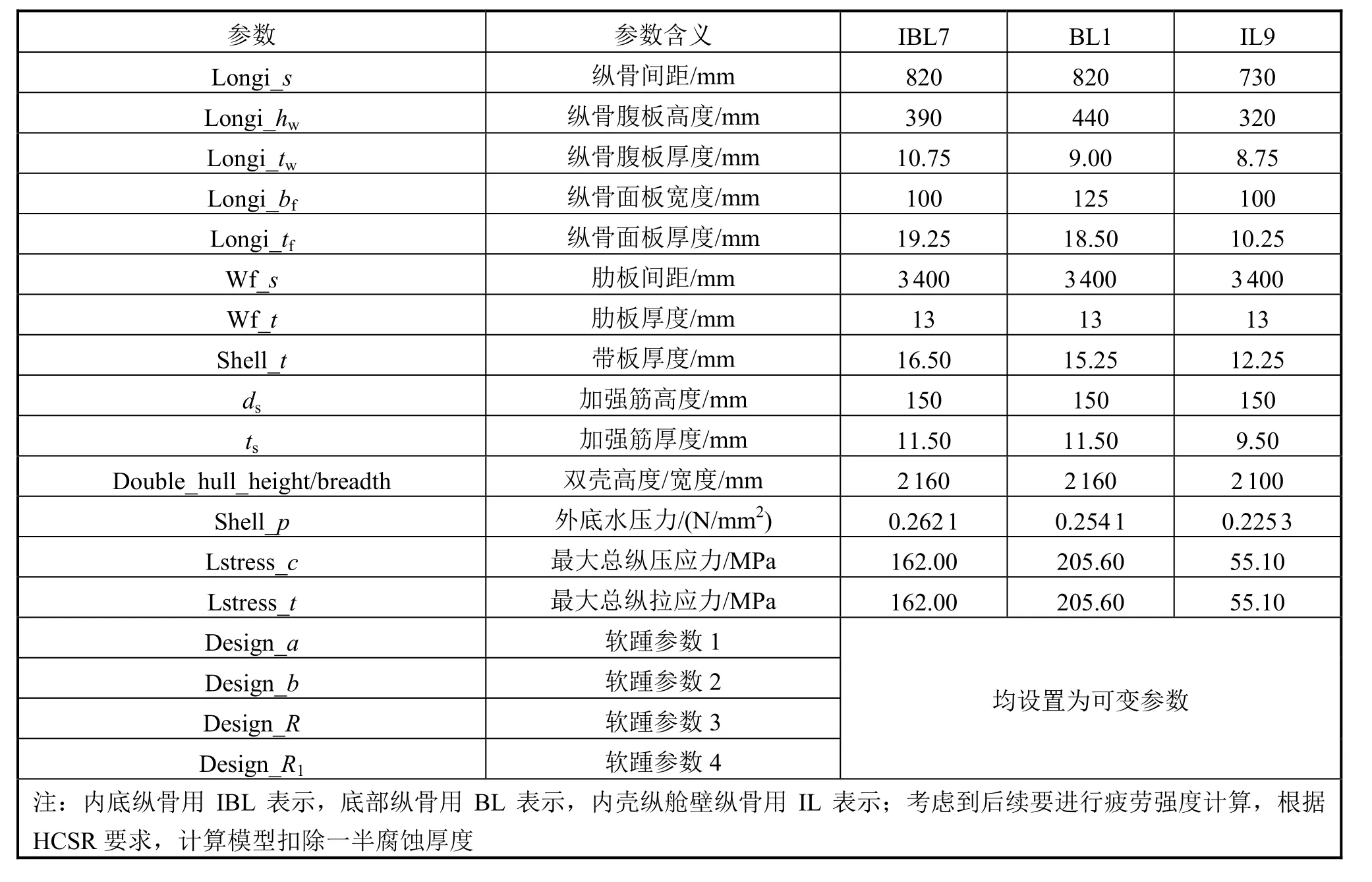
表1 各位置下的主要模型参数取值

表2 纵骨挺筋软踵参数初值（依据船厂典型节点图册） mm

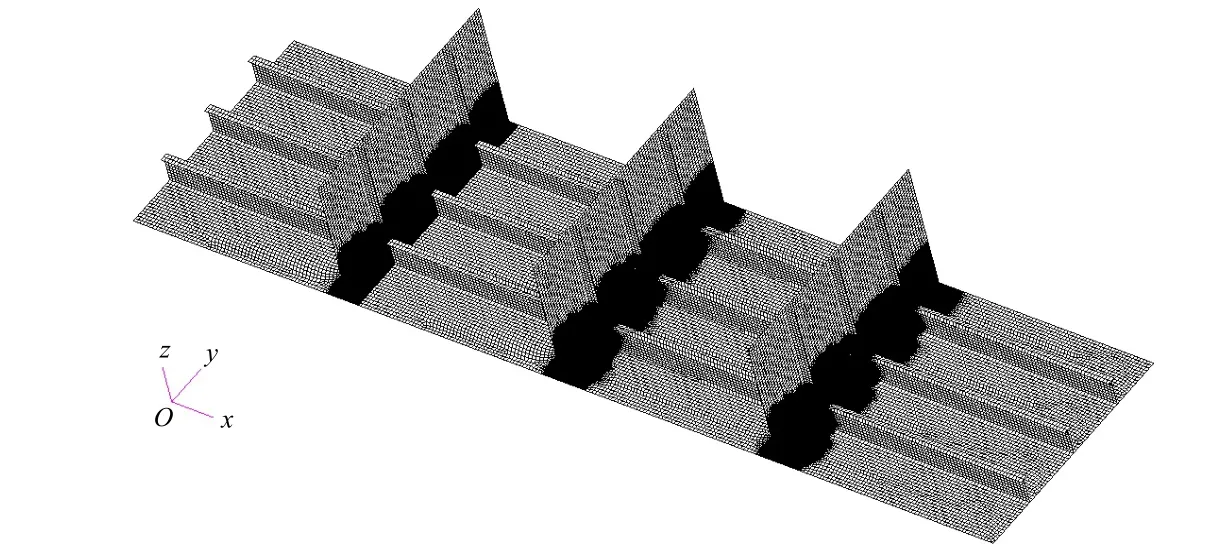
图5 整体参数化模型

由于在优化计算过程中需要反复建立有限元模型，因此采用PCL语言编程[1-2]，能根据不同参数快速准确地完成计算模型的生成。同时，在建立参数化模型过程中，为增强模型未来面向其他船型的实用性，将模型的尺寸都设定成可变参数，得到的参数化模型可应用于不同纵骨间距、不同强框间距、不同载荷大小及不同双壳高度的结构，能快速校核、对比不同设计方案的应力情况，并可将此参数化模型作为双层底整体尺寸优化的基础。当然，在优化软踵参数时，仅需在优化过程中修改软踵参数。纵骨挺筋软踵有限元模型见图6。

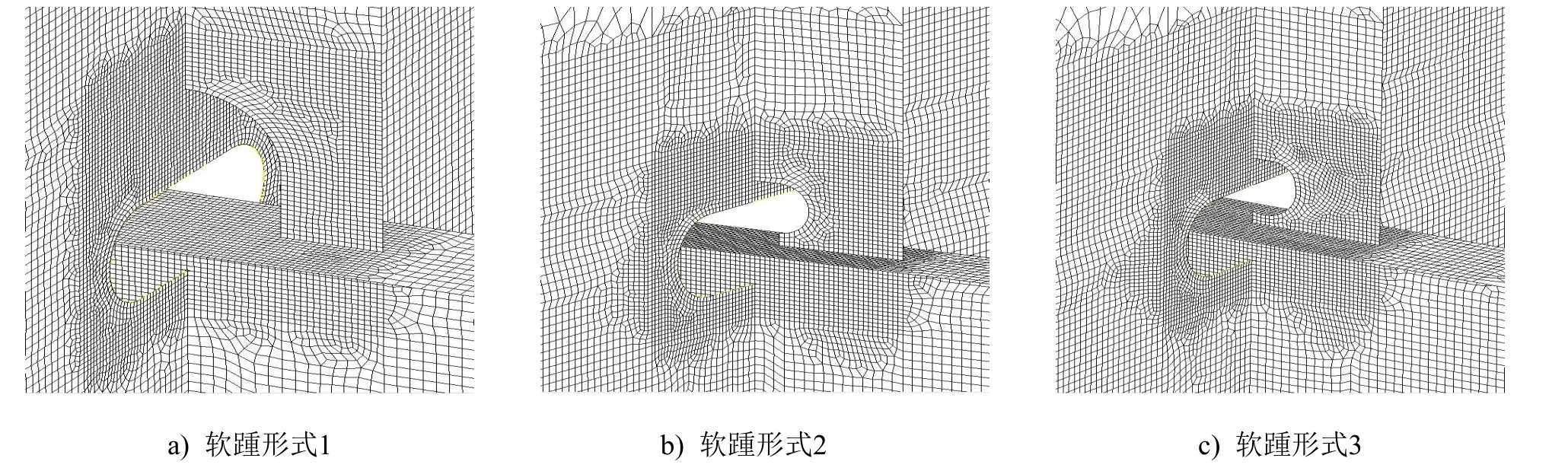
图6 纵骨挺筋软踵有限元模型

2.2 Isight集成通用有限元软件Patran和Nastran

Isight为多学科综合优化平台，能将优化流程中涉及的多个软件集成到一个平台上，并选取合理的优化算法进行优化求解，极大地提高优化效率[3]。利用Isight集成通用有限元软件Patran和Nastran进行优化设计，得到纵骨挺筋软踵的最优形状参数。Isight主要优化流程见图7。

该优化过程具体包含以下3个模块。

1) 第1个模块为ForXDB，主要包含2方面内容：一是调用Patran建立有限元模型，并生成Nastran求解文件（bdf文件）；二是调用Nastran进行计算，得到有限元模型的应力和位移结果文件。

图7 Isight主要优化流程

2) 第2个模块为ForResults，主要是调用Patran进行计算结果的后处理。由于Nastran的计算结果文件中没有最大应力的信息，故需要在Patran中进行最大应力单元的提取，并输出应力峰值到文本文件中，供Isight解析。

3) 第3个模块为DelFiles，在调用Patran和Nastran进行建模与分析的过程中，软件会产生很多中间文件，这些文件只需在优化过程中使用，没有必要保留，因此每次迭代后需要删除。该模块的主要功能是删除优化过程中产生的中间文件。

3 优化结果及分析

3.1 初始模型合成应力计算结果

下述合成应力均指von-mises应力，虽然t×t网格大小的合成应力并不能直接与HCSR关于细网格的许用应力要求相比较，但能较为准确地反映热点区域的单元应变能力分布情况；同时，可在不跨越板缝的条件下对50mm×50mm范围内的合成应力求平均值后与HCSR相应的许用应力要求相比较，以校核该区域的屈服强度是否满足规范要求。以下疲劳强度计算所基于的应力均为单元最大主应力，不再赘述。

图8为3种软踵形式下初始模型合成应力分布。3个不同船体位置处纵骨与附连挺筋有限元模型的应力分布趋势大致相同，故仅以底部纵骨应力分布图为示例，其他位置仅列出应力峰值，具体初始模型合成应力极值见表3。

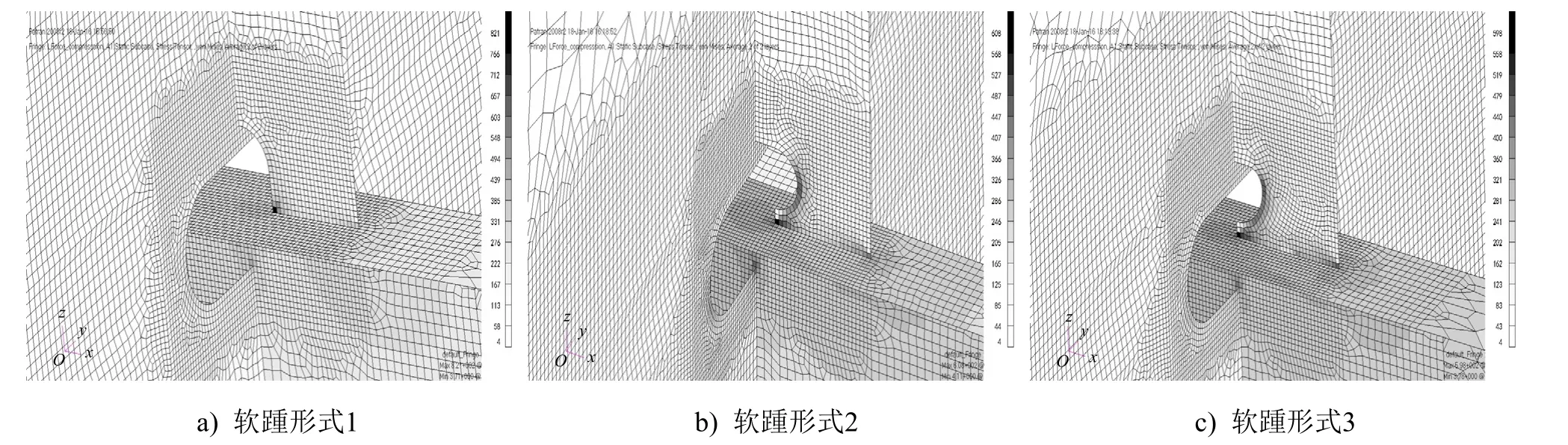
图8 3种软踵形式下初始模型合成应力分布

表3 初始模型合成应力极值 MPa

由计算结果可知：3种软踵下端均出现应力集中现象，软踵形式1的应力集中现象最为严重，后2种软踵形式的应力分布比较均匀且应力极值相对较小；另外，从应力分布情况看，3种软踵形式都是在开孔边缘处应力较大，并向四周迅速减小，故优化方向应该是以减小开孔边缘应力为导向，尽量减小开孔边缘的应力极值。

3.2 优化计算结果

3.2.1 优化算法

优化过程中，采用Isight中自带的多岛遗传算法（MIGA）进行优化计算。MIGA是传统遗传算法的一种改进算法，与传统的并行分布式遗传算法相比具有更强的全局寻优能力，且计算效率更加优良。

MIGA相对于传统遗传算法的一个主要特点是在求解时将一个大的种群分割成多个小种群，称其为“子种群”或“岛”，之后再对各个子种群进行传统的遗传算法优化计算，包括选择、交叉及变异等过程，寻求每个子种群中的最优个体；同时，在各个子种群之间需进行个体信息交流，以获取总体最优个体。因此，MIGA比传统的遗传算法多一步“迁移”操作，具体操作为：每隔一定代数，按一定比例从各个子种群中挑选一定数量的个体转移到其他子种群中，从而增加各个子种群中个体的多样性；在反复进行优化筛选后，保留下来的个体适应性越来越强，最终得到最优的个体。“迁移”过程可有效地抑制遗传算法的早熟现象，大大增加算法的全局寻优能力，从而更好地获得全局最优解[4]。

3.2.2 优化计算结果

以软踵及其附近结构的屈服强度裕度最大为目标函数，得到不同形状参数下的最优开孔尺寸见表 4～表6。

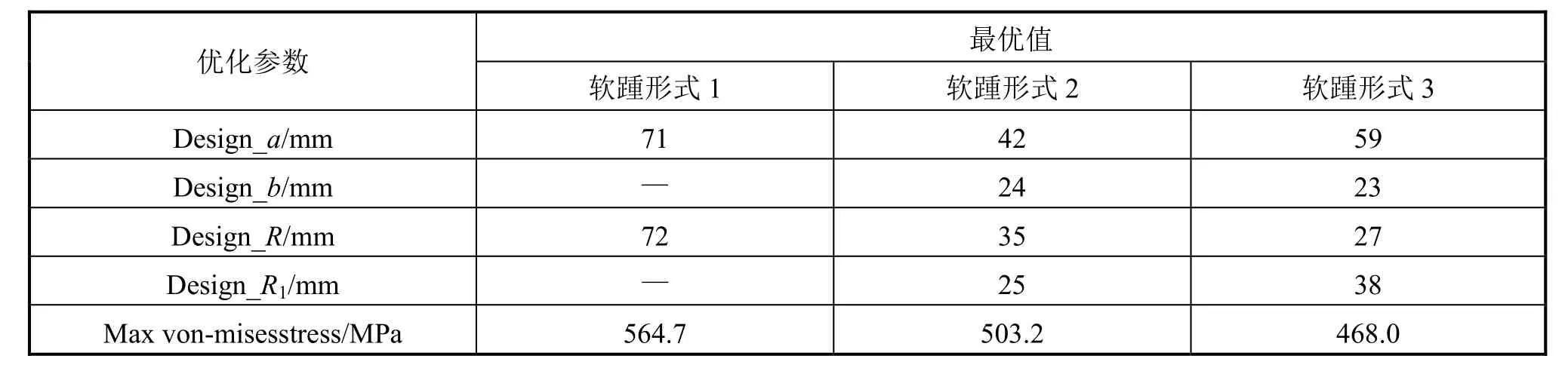
表4 BL处优化计算结果

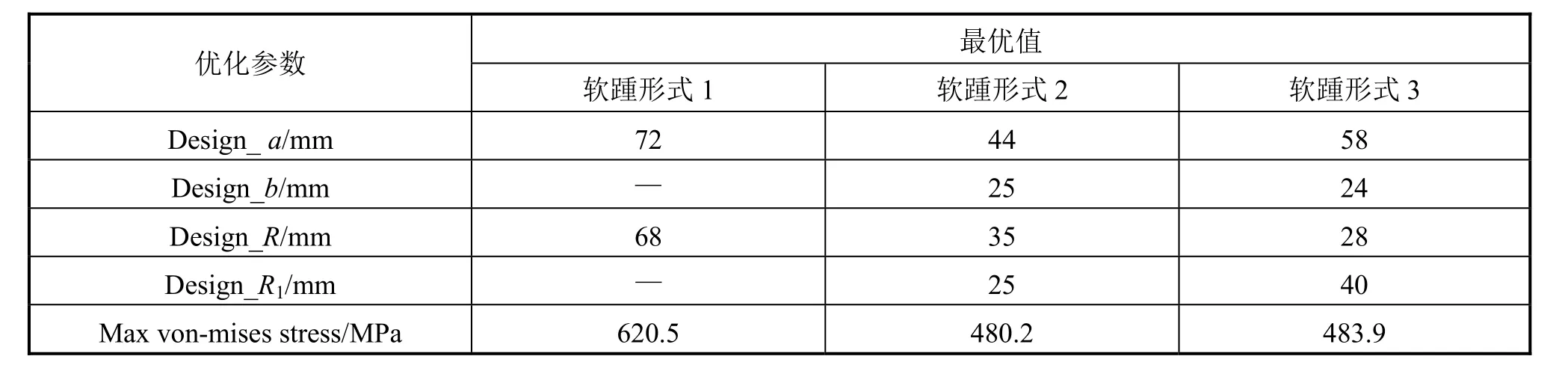
表5 IBL处优化计算结果

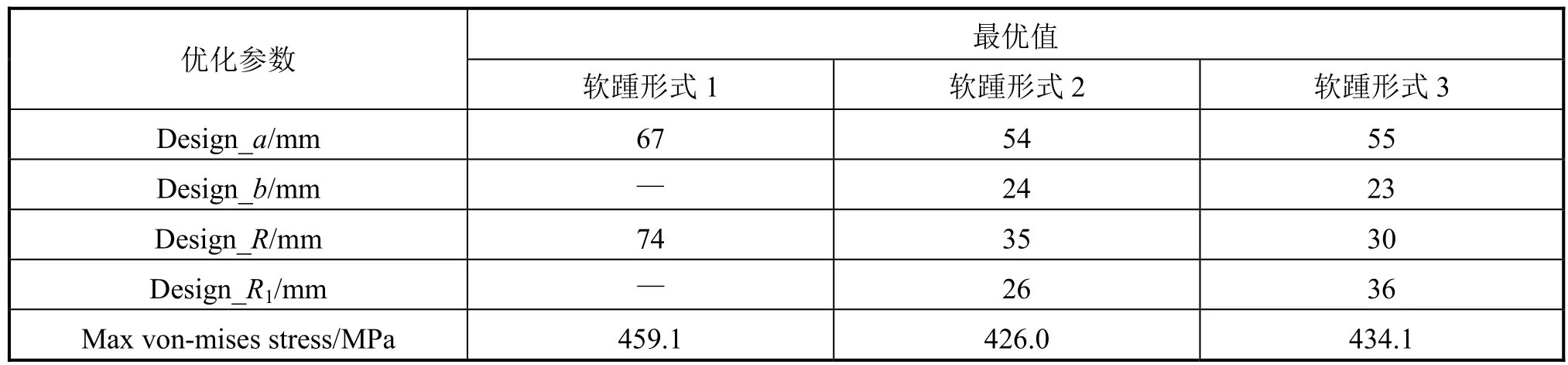
表6 IL处优化计算结果

由表4～表6可知，内底纵骨和外底纵骨处的最优软踵开孔尺寸比较接近，实际工程中可考虑将内底和外底的纵骨挺筋软踵设计成同种类型及尺寸，以方便施工建造；舷侧的纵骨挺筋最优软踵尺寸与底部的纵骨挺筋最优软踵尺寸差别较大，需要单独设计，以降低舷侧纵骨挺筋处的应力极值。

各模型在优化过程中的最大应力变化及最优开孔尺寸下的应力分布见图9～图11（限于篇幅，仅列出BL1处3种软踵优化过程中的应力变化曲线，另外2处的情况与BL1相似）。优化前后软踵有限元模型合成应力峰值对比见表7。

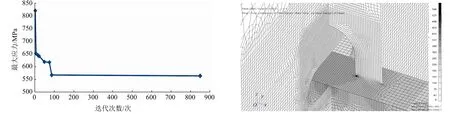
图9 模型1优化过程及最优尺寸下应力分布

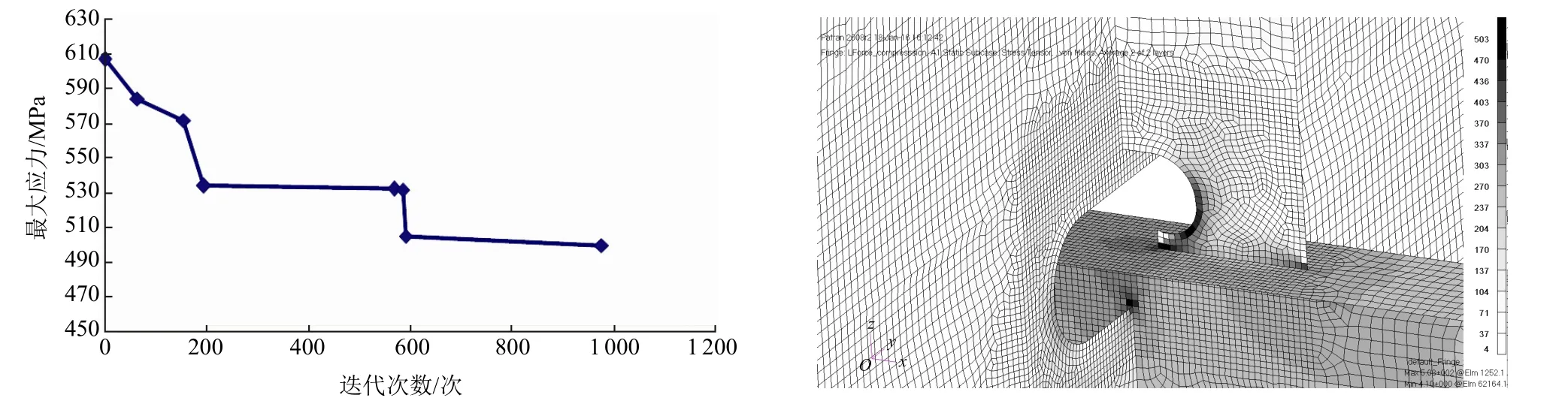
图10 模型2优化过程及最优尺寸下应力分布

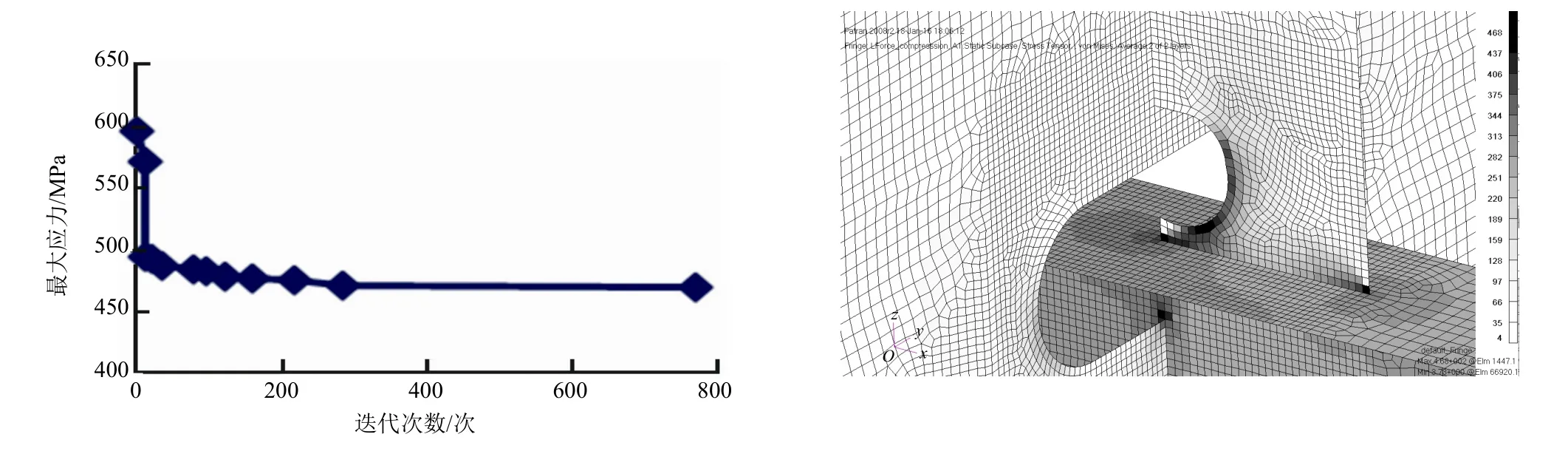
图11 模型3优化过程及最优尺寸下应力分布

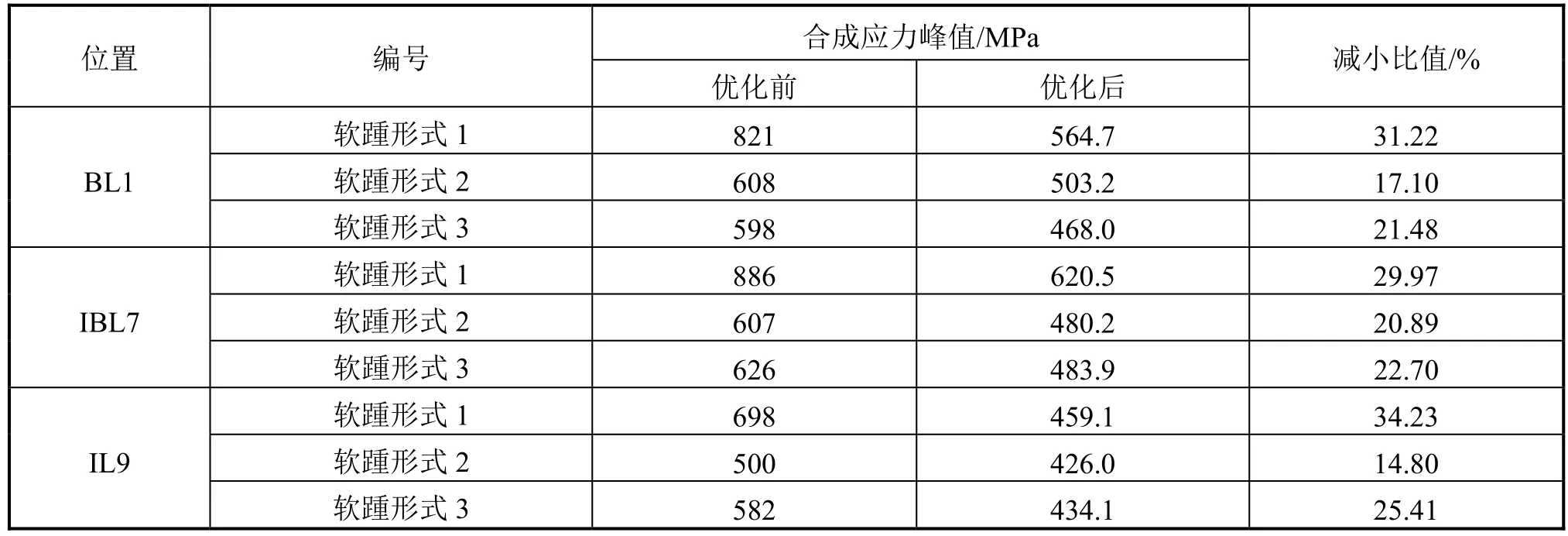
表7 优化前后软踵有限元模型合成应力峰值对比

由表7可知，3种开孔形式下通过Isight优化后应力峰值都有明显的减小，优化效果显著。

1) 模型1的开孔形式在实际工程中应用较多，主要原因是开孔形式简单、施工方便，但应力集中现象明显，若未经优化设计，则应力峰值较高，容易出现局部结构损坏；

2) 模型2和模型3的开孔形式较为复杂，施工麻烦，但开孔周围应力分布更为均匀，应力集中现象有很大程度的减弱，应力峰值也更小，更能保证结构的安全性和可靠性。

此外，软踵形式1的优化结果在具体应用中还存在以下2方面问题。

1) 由有限元计算结果可知，软踵形式1中通焊孔的半径在接近挺筋腹板高度的一半时应力峰值最小，但实际上这种开孔形式在纵骨与附连挺筋的焊接连接面积方面远不满足 HCSR中关于焊缝连接面积的要求，因此软踵形式1得到的最优解并不能超越规范直接应用到工程结构中。

2) 软踵形式 1的初始解虽然满足规范关于纵骨与附连挺筋焊接连接面积的要求，但由于应力峰值较大，在应力峰值附近不跨越板缝50mm×50mm范围内的合成应力加权平均值达到550MPa左右，超过了HCSR规定的临近焊缝处、考虑动载荷时的许用应力452MPa，因此虽然软踵形式1在工程实际中被大量应用，但存在一定的安全隐患。相比之下，软踵形式 2和软踵形式 3在焊接连接面积方面能很好地满足HCSR的要求，且在应力分布上也更优于软踵形式1。

由于软踵形式3相比软踵形式2在纵骨与附连挺筋焊接连接长度方面更优，故在纵骨与附连挺筋焊接连接面积方面更容易满足HCSR的要求。

3.3 疲劳强度校核

为保证纵骨和挺筋的疲劳寿命，需要对优化所得结构形式进行疲劳强度校核。这里按照HCSR对船体结构疲劳寿命的相关要求进行校核，为准确计算焊缝处的单元主应力，模型单元尺寸选为0.5t × 0.5t。主要计算纵骨面板、腹板和软踵开孔自由边的疲劳寿命，所得疲劳寿命计算结果见表8。

表8 疲劳寿命计算结果 a

由于软踵形式1的优化后尺寸焊接连接面积不足，因此采用满足连接面积要求的初始尺寸作为比较对象。由表8可知，双底、双壳内3个位置处的纵骨腹板和挺筋软踵疲劳寿命都能满足HCSR对船体结构疲劳寿命的要求，但双底内纵骨BL1和IBL7若采用软踵形式1，则在软踵自由边处的疲劳强度不满足规范要求。

对于不同位置处的软踵形式，纵骨面板和纵骨腹板的疲劳寿命相差不大，而软踵自由边处的疲劳寿命相差较大，软踵形式2的自由边疲劳寿命要略优于软踵形式1和软踵形式3。产生这种现象的原因在于优化目标是使软踵及其附近结构的屈服强度裕度最大（亦即减小整个区域内结构合成应力的极值），而由合成应力的分布图可知其极值均位于软踵自由边缘上，故优化过程主要以减小自由边的应力极值为导向，所得的最优解能有效延长自由边的疲劳寿命，而对纵骨面板或腹板疲劳寿命的影响较小。

为验证不同优化目标对不同位置处疲劳寿命的影响，增加以纵骨面板的疲劳寿命（亦即面板纵向最大主应力最小）为优化目标的算例，计算结果见表9。

表9 以纵骨面板疲劳寿命为优化目标的算例计算结果 a

由表9可知，若以纵骨面板的纵向最大主应力为优化目标，则能提高纵骨面板的疲劳寿命。虽然这种优化目标下的最优尺寸对软踵开孔自由边疲劳寿命提高的作用不如前述优化结果，但可有效提高整个局部结构所有关键节点疲劳寿命的“短板”，对提高节点的整体疲劳寿命有益。因此，未来软踵形状参数优化的目标函数既要考虑软踵附近结构的应力极值，也要考虑纵骨面板的疲劳强度，真正意义上的结构形状最优解将在两者之间产生。

4 结 语

基于PCL参数化建模技术，在Isight软件中集成了Patran和Nastran两大商用建模计算软件，建立了船体结构纵骨上附连挺筋软踵形式的优化流程，并选用MIGA对开孔参数进行了优化计算和分析，得出以下结论：

1) 利用PCL参数化建模技术能快速准确地建立有限元分析模型，极大地提高有限元建模和分析效率，并能免除优化过程中的人工参与过程，可有效减少建模时间，使设计人员更多地关注结构的设计和计算。

2) Isight能集成不同的软件平台进行优化计算，使设计人员根据需要设定相应的优化算法或选用Isight自带的优化算法、调用不同的软件进行优化计算，弥补了某些软件没有优化功能的缺陷，扩展了优化设计的应用范围，也使得不同软件之间的数据交流更加方便。

3) 通过优化计算得到的纵骨挺筋软踵形式在应力分布方面要明显优于设计人员凭经验设计的软踵形式，能有效提高结构的安全性和可靠性，证明提供的优化计算方法有实际工程应用价值，值得推广应用到其他类似结构的优化设计中。

4) 通过优化计算得到的纵骨挺筋软踵形式2和软踵形式3的疲劳寿命均满足HCSR对船体结构疲劳寿命的要求，有足够的安全性和可靠性；考虑到软踵形式3的屈服应力水平和疲劳寿命均与软踵形式2大致相当，且不会出现与纵骨之间焊接连接面积不足的情况，故认为软踵形式3更值得推广应用到实际工程中。

5) 建立的参数化模型可作为进一步优化双层底整体尺寸的基础，对双层底结构作进一步的轻量化设计。

[1] 何祖平，王德禹. 基于MSC.Patran二次开发的结构参数化建模及其集成开发环境[J]. 船海工程，2005 (2): 17-20.

[2] 马静敏，沈友徽，李华. 基于Isight的油船槽形横舱壁优化设计[J]. 船海工程，2005 (1): 35-37.

[3] 牟淑志，杜春江，牟福元，等. 基于多岛遗传算法的连续体结构拓扑优化设计[J]. 机械科学与技术，2009, 28 (10): 1316-1320.

[4] International Association of Classification Societies. Harmonized Common Structural Rules for Bulk Carriers and Oil Tankers [S]. 2014.

Shape Optimization of the Stiffener Soft Heel Attached to Longitudinals

LUO Ren-jie，QIU Wei-qiang，CAI Shi-jian，Chen Tao

（Marine Design & Research institute of China, Shanghai 200011, China）

The stiffener attached to hull longitudinals is one of the most typical structural nodes in ships. Stress concentration would occur when a sudden geometrical change happens at the intersection point of the attached stiffener and the plate of longitudinals, which may lead to structure failure or damage. According to the diagrams illustrated in the Harmonized Common Structural Rules (HCSR) and the drawings of typical structural nodes produced by the domestic shipyards, three types of stiffener soft heel are chosen to establish parametric models. Finite element modelling software Patran and calculation software Nastran are integrated into Ishight to realize shape optimization and to obtain the soft heel shape with the minimum stress extremum. Meanwhile, the fatigue strength of the three types of optimal soft heel is checked according to HCSR, and their fatigue lives corresponding to different opening shapes are compared. The result shows that the proposed optimization procedure can effectively reduce the stress extremum of the structure, increase the fatigue life, and obtain the optimized opening shape and parameters at different hull locations with better fatigue strength and yield strength. It has good application value and could be used for the node design of other similar structures.

ship and naval architecture; longitudinals; soft heel; PCL parametric modeling; shape optimization; fatigue strength

U661.4

A

2095-4069 (2016) 06-0039-010

2016-02-18

工信部高技术船舶科研项目（工信部联装[2014]507号）

罗仁杰，男，硕士生，1990年生。就读于中国船舶及海洋工程设计研究院船舶与海洋结构物设计制造专业，主要从事船体结构优化设计工作。

10.14056/j.cnki.naoe.2016.06.008