基于KMC-KECA的间歇发酵过程的故障诊断

解亚萍，赵鹏，党伟明

(内蒙古工业大学 电力学院，呼和浩特 010051)

Φeca=PUkΦ=

基于KMC-KECA的间歇发酵过程的故障诊断

解亚萍，赵鹏，党伟明

(内蒙古工业大学 电力学院，呼和浩特 010051)

针对间歇发酵过程的不稳定性、强非线性、批次不等长等特点以及传统贡献图难以找到由特征空间到原始空间的逆映射函数的问题，提出了一种基于K均值聚类贡献图的核熵成分分析的间歇发酵过程故障诊断方法。首先，KECA算法按照Renyi熵值的大小选取特征值及特征向量，然后用K均值聚类中心作为当前时刻的标准样本，拿故障样本的每个变量依次去替换标准样本的对应变量，通过计算其统计量，找出故障源，从而进行故障诊断。最后将该方法用到青霉素发酵过程验证所提出方法的有效性。

核熵成分分析K均值聚类贡献图 故障诊断 间歇过程

由于间歇发酵过程数据存在高度非线性、耦合、数据缺损等问题，以主成分分析PCA(principal component analysis)和偏最小二乘PLS(partial least square)等为核心技术的多元统计过程监控方法(MSPM)可以从含有噪声的高维数据中提取出反映过程特征的低维变量。因此，MSPM方法近年来得到了长足的发展。MSPM的核心思想是通过数据投影将输入空间划分为特征子空间和残差子空间从而达到降低数据维数的目的[1]。其中，PCA算法的应用最为普遍，它可以有效将含噪声且相关的高维数据以保留原始数据的最大方差的原则投影到低维空间。但是，PCA算法只能处理线性数据[2-3]，它对于非线性过程的监控效果并不理想。Scholkopf等[4]提出了核主元分析(KPCA)算法，KPCA算法是通过非线性映射将低维输入空间映射到高维特征空间，在特征空间中进行PCA分析，从而把输入空间的非线性问题转化为特征空间中的线性问题[5-6]。Jenssen[7]在KPCA算法的基础上提出了核熵成分分析KECA(Kernel Entropy Component Analysis)算法，它是在KPCA算法的基础上引入熵的概念，在特征空间按照Renyi熵值的大小选取特征值和特征向量以实现数据转换，体现出了良好的非线性处理能力，在特征提取方面表现出了其独特的优越性。KECA 算法通过将输入空间投影到KPCA 主轴上实现数据的转换和降维[8]。

通常基于PCA的故障诊断方法有贡献图方法和故障重构方法。由于核函数方法无法提供测量变量到监控统计量之间的对应关系，因而在KECA算法中贡献图方法的应用就受到了限制。而故障重构的诊断方法，需要大量的历史故障数据，难以应用到无法获得大量故障数据的过程[9]。

针对故障重构和贡献图方法应用在KECA算法中的局限性，通过直接对故障时刻的监测样本进行重新构造，提出了一种新的故障诊断策略，即基于KMC-KECA的故障诊断方法。当某一时刻监测到当前样本发生了故障，找到当前时刻的标准样本，本文用K均值聚类中心，然后用故障样本的每个变量依次对应去替换标准样本，替换后重新做过程监测，计算统计量，判断其是否依然报警，如果报警，说明此时替换的那个变量就是故障变量，这样就可以找到故障源。

1 基于KMC-KECA的间歇发酵过程的故障诊断

1.1 对间歇发酵过程三维数据沿AT方法展开

三维数据矩阵X(I×J×K)代表间歇过程数据集合，其中：I代表批量数，J代表变量数，K代表采样点数。传统MKPLS预处理方法有沿批次方向展开和沿变量方向展开2种，根据MKPLS得出的参数建立监控模型。但是传统的方法存在批次不等长、数据填充等问题，笔者将建模的三维历史数据先沿批次方向展开，按列进行标准化处理，之后再沿变量方向展开，建立统计模型[10]，如图1所示。

图1 三维数据展开方法

1.2 KECA算法原理

KECA算法通过核映射首先将数据从低维输入空间投影到高维的特征空间，然后在特征空间内依据Renyi熵值的大小选取特征实现数据降维，降维后的数据分布表现出一定的角度结构，即不同特征信息之间呈现出显著的角度差异。KECA算法简要描述如下：

给定N维样本x，p(x)是概率密度函数，则其Renyi熵计算公式为[11]H(p)=-log∫p2(x)dx；由于对数函数为单调函数，可以令V(p)=∫p2(x)dx，采用Parzen窗通过样本均值对其进行估计得到：

(1)

式中：K——N×N的核矩阵，I——元素均为1的N×1的向量。

Renyi熵估计可由核矩阵的特征值和特征向量来表示，将核矩阵进行特征分解K=ΦTΦ=EDET，D为特征值矩阵，D=diag(λ1， …，λN)，E为特征向量矩阵，E=(e1， …， eN)，计算得到：

(2)

将N维数据通过Ф映射到由k个KPCA主轴张成的子空间Uk上，选取对Renyi熵贡献较大的前k个特征值和特征向量，可以得到转换后的数据：

Φeca=PUkΦ=

(3)

样本外数据投影到Uk上的计算公式[12-13]：

(4)

KECA算法可以表述为使核空间数据均值向量的平方欧氏距离与转换后数据均值向量的平方欧氏距离之差尽可能小。为了能够更多地保留原始数据的信息，在数据降维时采用熵值贡献率来确定选取主元的个数。

(5)

(6)

(7)

KECA算法实质是一种数据转换方法，它可以最大限度地保留核空间数据均值向量的欧氏距离。

从理论上来说，KECA算法可以获得优于KPCA算法的降维效果。这是由于KECA算法中

的特征向量能保证信息熵的减少最小，根据熵值最大程度地判断并保留主要特征信息，从而更好地保留了输入高维数据的原始特征，在较低维数时即能呈现较好的降维结果，具有更强的非线性处理能力。

KECA算法和KPCA算法对TE过程的故障1以及故障10的检测结果[13-14]如图2，图3所示，TE过程2种故障的检测延迟、故障检出率和误报警率见表1所列。

图2 对TE过程故障1的监测结果

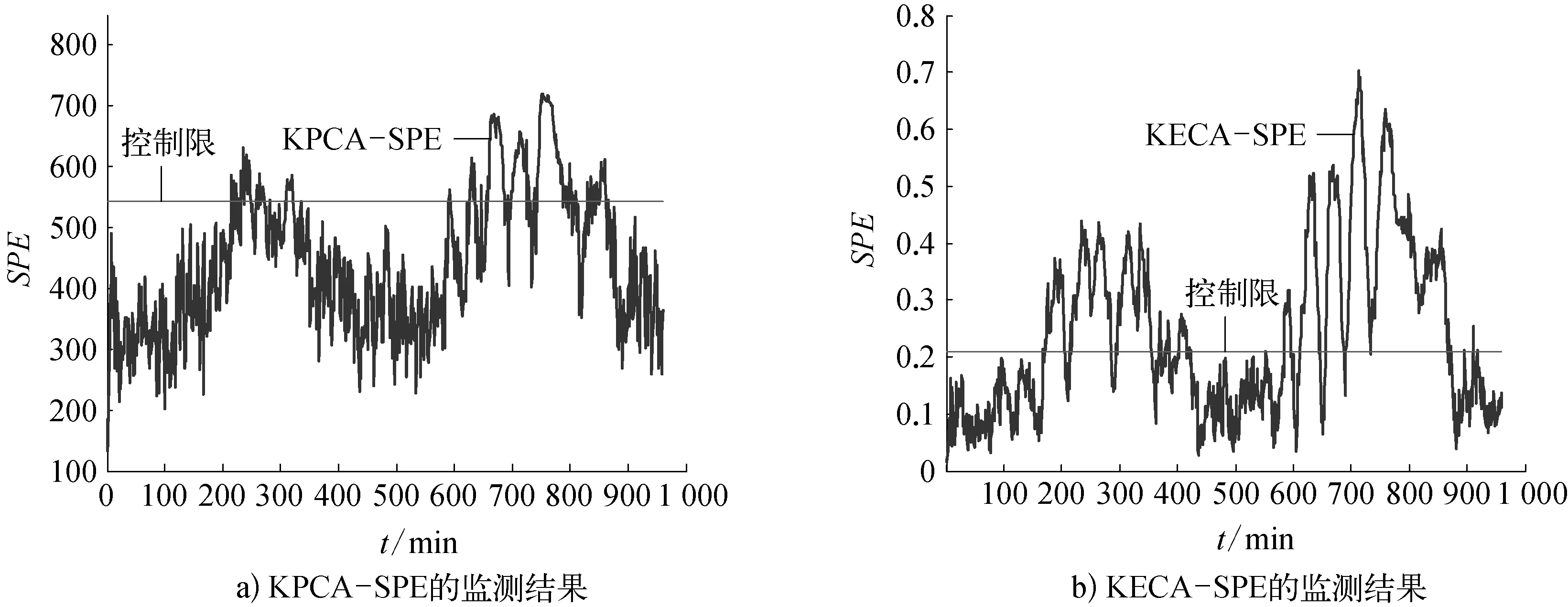
图3 对TE过程故障10的监测结果

故 障检测延迟/min故障检出率,%故障报警率,%KPCA-SPEKECA-SPEKPCA-SPEKECA-SPEKPCA-SPEKECA-SPE故障18699.5099.4036.900.63故障1080734.6061.5026.301.25

从图2，图3以及表1可以看出KECA在故障检测延迟、检出率、报警率方面相比于KPCA都有很大的优势。此外，在实际问题中，经常会出现小样本问题。研究表明，当高斯核函数的宽度参数σ过小时，KPCA降维能力受小样本问题影响较大，但KECA却能体现出解决此类问题的优越性，可以显著提高分类精度。

1.3 一种新的故障诊断方法

用基于KMC方法对间歇发酵过程故障进行识别。该方法是将沿批次展开的正常建模数据进行标准化处理以后，对每个时刻的每个变量分别求其在所有批次方向上的K均值聚类中心，然后再沿边量进行展开。质心向量的选取具体过程如图4所示。

图4 质心向量的选取过程示意

该方法具体实现步骤如下：

1) 原始数据沿批次展开、标准化，求每列K均值聚类中心，得到K(1×KJ)然后再沿变量方向进行展开。

2) 在线监测中一旦检测到故障发生，将K(1×KJ)中对应的第k时刻的J个值取出来，记为向量nor(1×J)，并令j=1。

3) 用test(1×J)中的第J个变量的值顺次替换nor(1×J)中第J个变量的值，替换后记作newtest(1×J)。

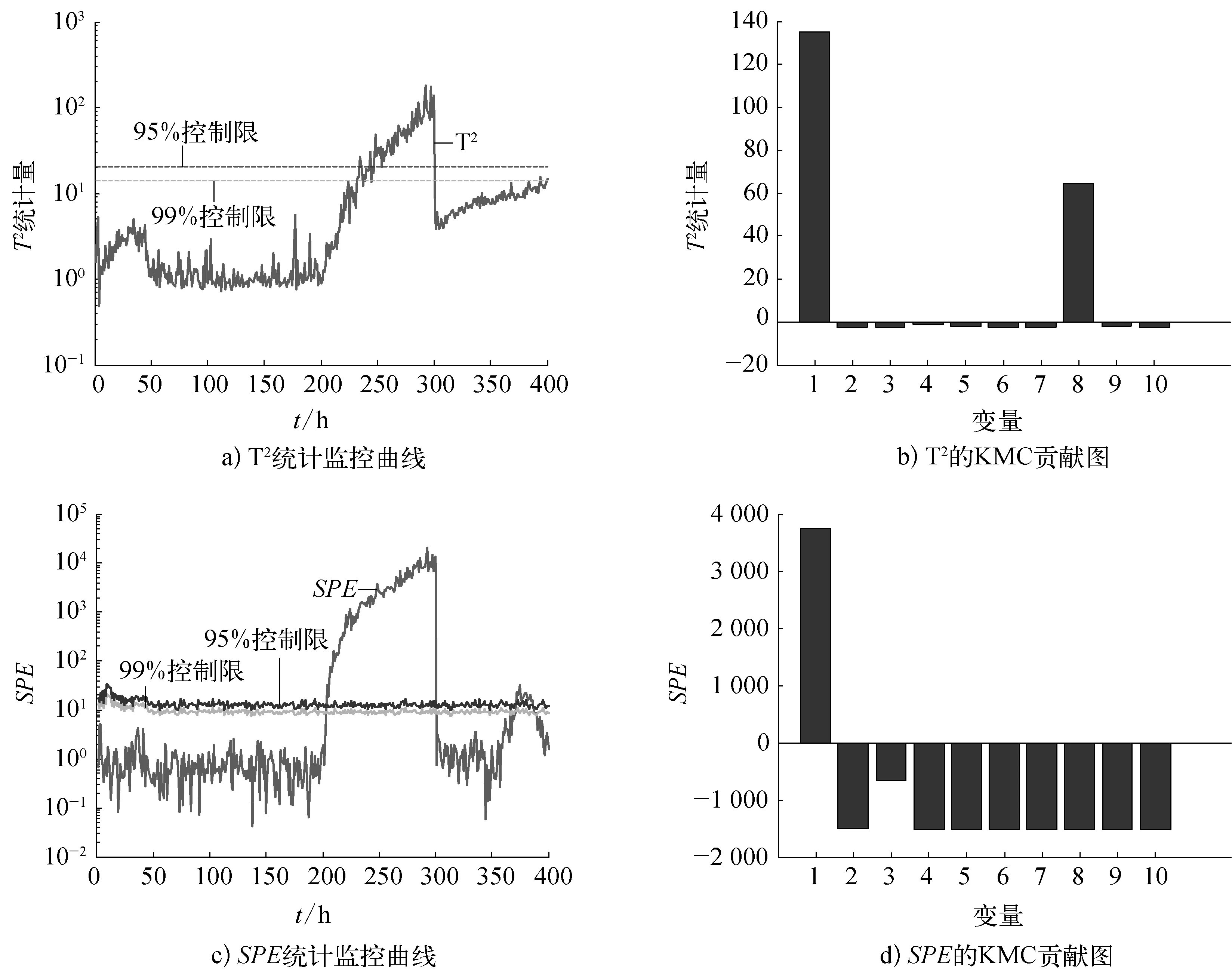
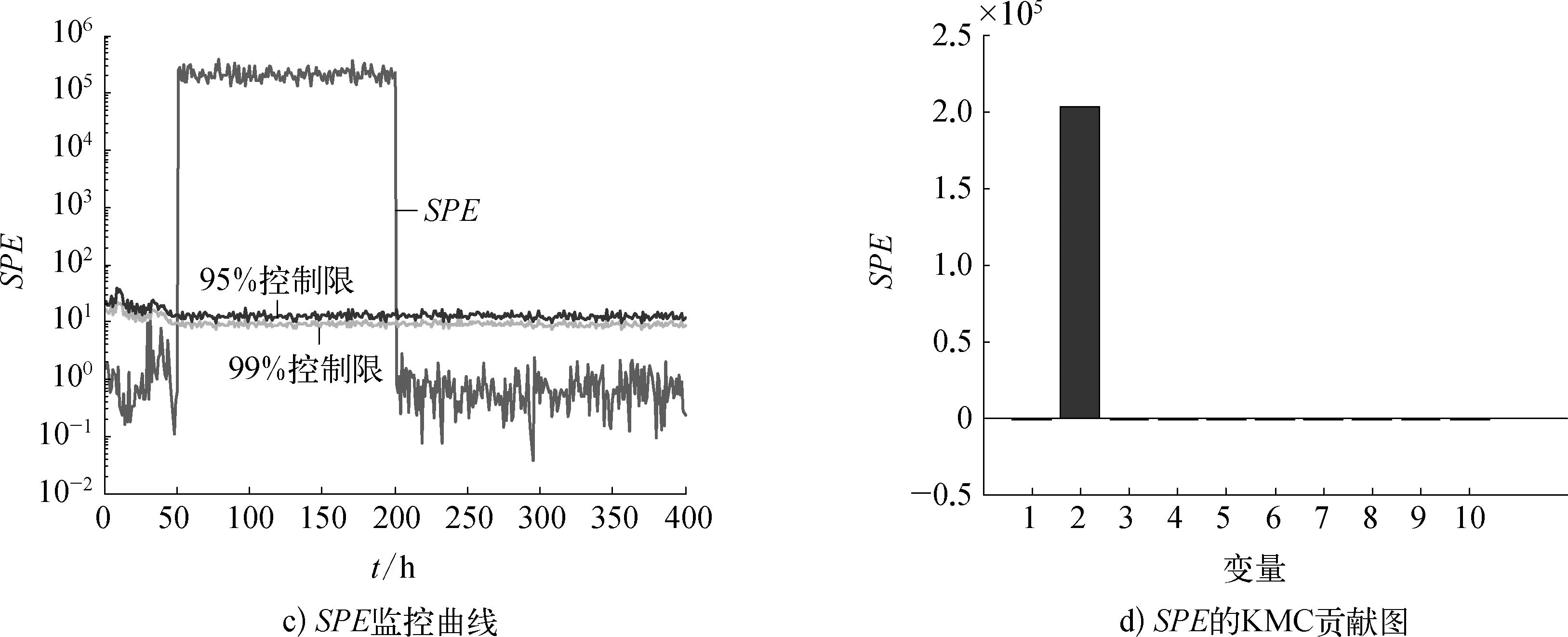
4) 再次计算newtest(1×J)的统计量值，并与当前第k时刻的控制限值相减，记录计算结果，如果j

5) 对步骤4)中的结果绘制直方图，相应直方图在正的方向的变量即为当前第k时刻的故障变量。

2 算法仿真验证

青霉素发酵过程是补料分批发酵过程，具有动态非线性和多阶段的特点。本文采用的 Pensim 仿真平台是由伊利诺科技学院IIT(illinois institute of technology)以Cinar教授为学科带头人的过程建模、监测及控制研究小组于1998—2002年研究开发的[14]。该仿真平台是专门为青霉素发酵过程而设计的，它为发酵生产的监视、故障诊断以及质量预测提供了一个标准平台。青霉素发酵过程每个批次的反应时间为400h，采样间隔是1h。Pensim仿真平台产生18个过程变量，笔者选择通风速率、搅拌速率、补料温度、溶解氧浓度、反应器体积、排出二氧化碳浓度、pH值、温度、产生热、冷水流加速度10个过程变量来构建统计模型，实现对产物浓度和菌体浓度的在线预测，并监控过程的运行。为了使训练样本数据可靠，同时令训练样本数足够多，笔者选择45个正常批次的数据作为模型参考数据库。

为验证提出算法的有效性，进行了3组实验，引入3种故障分别用T2和SPE两种统计量进行监控，并用KMC的故障诊断方法分别画出其贡献图。通过累计贡献率方法确定选取9个主元。

1) 实验1。在200～300h时，变量通风速率x1引入2%的斜坡故障，其监控结果与诊断结果如图5所示。

图5 故障1的诊断结果

从图5a)中看出在240h时刻监测到故障发生，图5b)中，变量1、变量8都大于0。但是变量1的作用更明显，有可能是2个变量有耦合性，从图5c)看出SPE在210h时刻发现故障，图5d)则明显看出变量1引起故障。

2) 实验2。在200～400h时，变量通风速率x1引入10%的阶跃故障，其监控结果与诊断结果如图6所示。

图6 故障2的诊断结果

从图6可以看出T2和SPE监控都在200h时刻超出控制限，两种统计量的贡献图均可以明显地判断引起故障原因。

3) 实验3。在50～200h时，变量搅拌速率x2引入10%的阶跃故障，其监控结果与诊断结果如图7所示。

从图7中看出在50h时刻T2和SPE监控都能及时监测到故障的发生，可以直观地找出引起故障发生的变量。

从上述3组实验可以看出KECA可以有效地对间歇发酵过程进行监测，而KMC贡献图方法也可以直观明确的对故障进行辨识，该实验证明KMC可以成功用于核空间的故障诊断中。

图7 故障3的诊断结果

3 结束语

本文针对间歇过程的强非线性以及传统贡献图方法应用在核空间中的局限性，提出基于KMC-KECA的间歇发酵过程的故障诊断方法，并对该方法进行理论分析，最后进行实验证，结果表明该算法可以有效地对间歇发酵过程进行诊断。

[1] XIONG L， LIANG J， QIAN J X. Multivariate Statistical Process Monitoring of an Industrial Polypropylene Catalyzer Reactor with Component Analysis and Kernel Density Estimation[J]. Chinese Journal of Chemical Engineering， 2007， 15(04)： 524-532.

[2] NOMIKOS P， MACGREGOR J F. Multivariate SPC Charts for Monitoring Batch Processes[J]. Technometrics， 1995(37)： 41-59.

[3] DONG D， MCAVOY T J. Nonlinear Principal Component Analysis-based on Principal Curves and Neural Networks[J]. Computer & Chemical Engineering， 1996， 20(01)： 65-78.

[4] SCHOLKOPF B， SMOLA A， MULLER K. Nonlinear Component Analysis as a Kernel Eigenvalue Problem[J]. Neural Computation，1998(10)： 1299-1319.

[5] LEE J M， YOO C K， CHOI S W， et al. Nonlinear Process Monitoring Using Kernel Principal Component Analysis[J]. Chemical Engineering Science， 2004(59)： 223-234.

[6] CHO J H， LEE J M， CHOI S W， et al. Fault Identification for Process Monitoring Using Kernel Principal Component

Analysis[J]. Chemical Engineering Science， 2005(06)： 279-288.

[7] JENSSEN R. Kernel Entropy Component Analysis[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2010，32(05)： 847-860.

[8] JIANG Q C， YAN X F， LÜ Z M， et al. Fault Detection in Nonlinear Chemical Processes Based on Kernel Entropy Component Analysis and Angular Structure[J]. Korean Journal of Chemical Engineering， 2013，30(06)： 1181-1186.

[9] 李洪强.基于核偏最小二乘的故障诊断方法研究[M]. 沈阳： 东北大学，2009.

[10] WESTERHUIS J A， KOURTI T， MACGREGOR J F. Comparing Alternative Approaches for Multivariate Statistical Analysis of Batch Process Data[J]. Journal of Chemometrics， 1999，(13)： 397-413.

[11] RENYI A. On Mearsures of Entropy and Information [C]. Selected papers of Alfred Renyi. 1976 (02)： 565-580.

[12] BIROL G， UNDEY C， CINAR A. A Modular Simulation Package Forfed-batch Fermentation： Penicillin Production[J]. Computers and Chemical Engineering (S0098-1354)， 2002，26(11)： 1553-1565.

[13] MAHADEVAN S， SHAH A L. Fault Detection and Diagnosis in Process Data Using One-class Support Vector Machines[J]. Journal of Process Control， 2009(19)： 1627-1639.

[14] LAU C K， GHOSH K， HUSSAIN M A， et al. Fault Diagnosis of Tennessee Eastman Process with Multi-scale PCA and ANFIS[J]. Chemometrics and Intelligent Laboratory Systems， 2013(120)： 1-14.

Fault Diagnosis for Batch Fermentation Process Based on KMC-KECA

Xie Yapin，Zhao Peng，Dang Weiming

(Institute of Electric Power， Inner Mongolia University of Technology， Hohhot， 010051， China)

Aiming at characteristics of instability， strong nonlinearity， non-even batch time and problem of difficulty to find inverse mapping function from feature space to original space from conventional contribution plot， a K-mean clustering-kernel entropy component analysis (KMC-KECA) fault diagnosis method is proposed. First mapped data from low dimensional input space into a high dimensional feature space to achieve nonlinear relationship between variable linear transformation. The data dimensionality reduction was conducted according to kernel entropy eigenvalues and eigenvectors. Then a KMC kernel space contribution plot of fault diagnosis method was proposed, fault diagnosis is achieved according reconfiguring monitoring sample of fault times by this method. At last， it was applied in fermentation process of penicillin fermentation. The results show better fault diagnosis performance is obtained with proposed method.

KECA; K-mean clustering-Kernel contribution plot; fault diagnosis；batch process

国家自然科学基金项目(61364009，21466026)；内蒙古自然科学基金项目(2015MS0615)；校级重点项目(X201237)。

解亚萍(1991—)，女，就读于内蒙古工业大学电力学院，研究方向为工业过程的故障诊断，硕士研究生。

TP277

B

1007-7324(2016)06-0021-06

稿件收到日期： 2016-09-16。