多险种多复合Poisson-Geometric常利率风险模型预警区问题

贺小丽,余国胜

(江汉大学数学与计算机科学学院, 湖北 武汉430056)



多险种多复合Poisson-Geometric常利率风险模型预警区问题

贺小丽,余国胜

(江汉大学数学与计算机科学学院, 湖北 武汉430056)

摘要：建立多险种多复合Poisson-Geometric过程的常利率风险模型,充分应用盈余过程的强马氏性,得到第一预警区的一个条件矩母函数所满足的积分-微分方程,当c=0时给出具体的实例以解释我们的结果.

关键词：利率;多险种多复合Poisson-Geometric风险模型;预警区;积分-微分方程

0引言

破产概率问题是保险核心问题之一，可以为保险公司决策者提供一个早期的风险警示.但是，假如保险公司可以从外部(或公司内部各业务之间)得到帮助，在未来的某个时间恢复过来，并把扭亏为盈的时间称为预警区，因此，预警区问题的研究是十分重要的.针对常利率的复合Poisson风险模型，于金西等[1]讨论了预警区的矩母函数及各阶矩.崔巍[2]在复合Poisson-Geometric风险模型下，对第一预警区问题进行了研究.文献[3]中考虑到利率的影响，建立一类带常利率复合Poisson-Geometric风险模型，充分应用盈余过程的强马氏性，针对指数索赔情形下给出其精确解.但是所研究的险种是单一的.然而，随着保险公司经营规模的不断扩大以及新险种的开发，用此风险模型来描述风险经营过程就具有一定的局限性.文献[4]中建立了多险种多复合Poisson-Geometric过程的常利率风险模型，得到了该模型的生存概率所满足的积分-微分方程.文献[5]中讨论了多险种多复合Poisson-Geometric常利率风险模型的折现惩罚期望函数.笔者则在此模型基础上，充分应用盈余过程的强马氏性,得到第一预警区的一个条件矩母函数所满足的积分——微分方程,当c=0时给出了具体的实例以解释我们的结果.

1模型引入

定义1.1设(Ω,F,P)为给定的完备概率空间，本文中所用到的随机变量均定义在此空间上.

设保险公司在t时刻(t≥0)的盈余U(t)满足如下方程：

(1.1)

其中,c>0是常保费率,δ≥0为常利率,

N1(t)～PG(λ1t,ρ1),N2(t)～PG(λ2t,ρ2),…,Nn(t)～PG(λnt,ρn),(0≤ρi<1,i=1,2,…,n),

此模型称为常利率多险种多复合Poisson-Geometric风险模型.

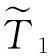
2预备知识及引理

以下考虑在常数利率δ下多险种多复合Poisson-Geometric风险模型，为此先给出Poisson-Geometric过程的定义如下:

定义2.2设λ>0,0≤ρ<1,称{N(t);t≥0}为参数λ,ρ复合Poisson-Geometric过程，如果满足：

(i)N(t)=0；

(ii) {N(t);t≥0}具有平稳独立增量;

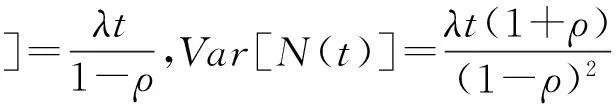
注2.1由定义2，当ρ=0时，复合Poisson-Geometric过程就是Poisson过程.因此，复合Poisson-Geometric过程是Poisson过程的一种推广.

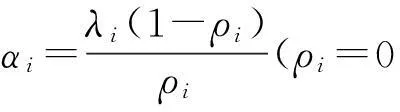
Pr{Ni(t)=0}=e-λit=1-λit+o(t),

3主要结果及证明

定理3.1记

对盈余过程由(0.1)式刻画的风险模型，第一预警区的条件矩母函数Φ(-z,0,r)满足积分-微分方程：

(3.1)

其中：Φ′(·)为Φ(·)关于-z取微分.

定理3.1的证明对充分小的dt,考察(T,T+dt]内的情形，分以下4种情况讨论.

1) 事件B1表示在(T,T+dt]内,{Ni(t),t≥0},i=1,2,…,n均无跳跃，其概率为

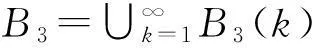
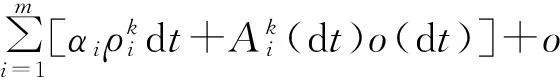
4) 其他情形，即{Ni(t),t≥0},i=1,2,…,n至少两个存在跳跃，此事件记为B4，其概率为o(dt).

由盈余过程的强马氏性，有

由全期望公式，我们有

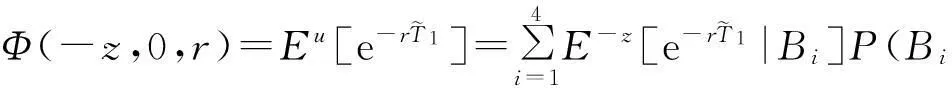
考虑事件B1,在时刻T+dt,U(T+dt)=-z+cdt,则

(3.2)

其中

e-rdtΦ(-z-y+cdt,0,r).

由单调收敛定理知∫与∑交换次序无问题，所以

(3.3)

考虑事件B3,则

(3.4)

(3.5)

(3.6)

(3.7)

由(3.4-3.7)式可得

(3.8)

考虑事件B4,我们有

E-z[e-rT1|B4]P(B4)=E-z[e-rT1|B4]o(dt)=o(dt)

(3.9)

根据式(3.2-3.3)式,(3.8-3.9)式整理可得

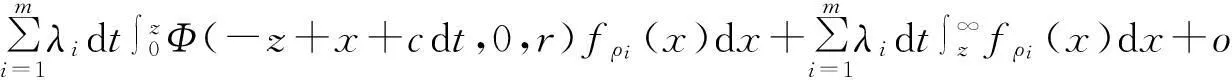
进一步整理，可得

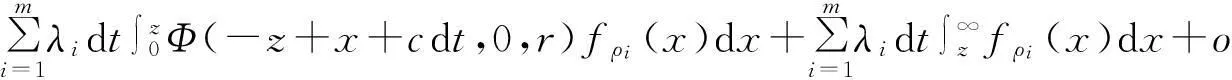
上式两边同时除以dt,并令dt→0,可得

即

注3.1当m=0,n=1,则(3.1)式为文献[3]中的定理(1).

4一个实例

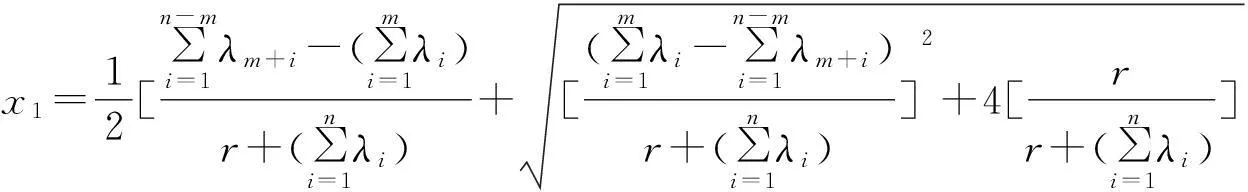
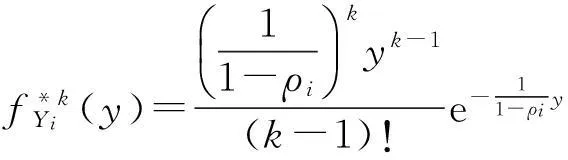
于是

(4.1)

由定理3.1,我们有

(4.2)

代换后可得

(4.3)

上式两边关于-z求偏导

(4.4)

将(4.3),(4.4)式两边相加，化简后可以得到

(4.5)

将(4.5)式两边关于-z求偏导

(4.6)

将(4.6),(4.5)式两边相减，整理后可以得到

(4.7)

(4.7)式的特征方程为

(4.8)

该方程有两个解，分别记为

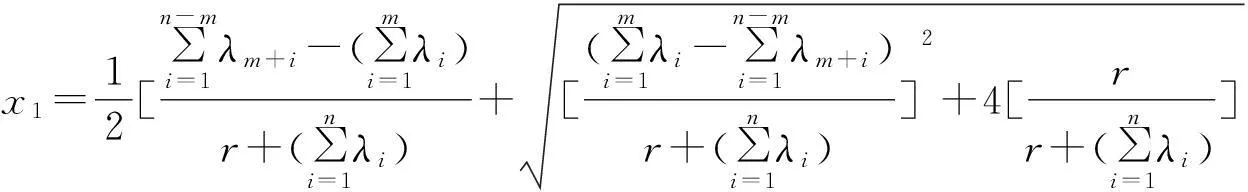
因此(4.8)式的通解形式为

Φ(-z,0,r)=C1e-x1z+C2e-x2z.

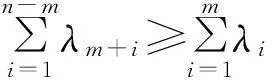
参考文献5

[1] 于金酉,胡亦钧,韦晓.常利率复合Poisson-Geometric风险模型中的预警区问题[J].数学物理学报, 2010, 30A(1): 1-17.

[2] 崔巍,余旌胡.一类推广的复合Poisson-Geometric风险模型下预警区问题的研究[J].数学物理学报, 2012, 32A(1): 27-40.

[3] 钟朝艳.一类常利率复合Poisson-Geometric风险模型的预警区问题[J]. 西南师范大学学报:自然科学版,2014, 39(3): 36-40.

[4] 李碧云,余国胜.多险种多复合Poisson-Geometric过程的常利率风险模型[J].湖北大学学报:自然科学版,2015, 37(3): 208-212.

[5] 李碧云,余国胜,姚春临,等.多险种Poisson-Geometric风险模型的折现惩罚期望函数[J].江汉大学学报:自然科学版,2015, 43(2): 101-104.

[6] 毛泽春,刘锦萼.索赔次数为复合Poisson-Geometric过程的风险模型及破产概率[J].应用数学学报,2005, 28(3): 419-428.

[7] GRANDEII. Aspects of risk theory[M].New York: Springer-Verlag, 1991.

(责任编辑赵燕)

Duration of negative surplus for the multi-compound poisson-geometric risk model of multi-type-insurance with a constant interest rate

HE Xiaoli, YU Guosheng

(School of Mathematics and Computer Science,Jianghan University, Wuhan 430056, China)

Abstract:A multi-compound Poisson-Geometric risk model of multi-type-insurance with a constant interest rate is constructed, by taking full advantage of the strong Marköv property of the surplus process,a integral-differential equation of a conditional moment genetating function for the first duration of negative surplus has been obtained. Finally, we give an explicit example to illustrate our results when c equals to zero.

Key words:interest rate; multi-compound Poisson-Geometric risk model of multi-type-insurance;duration of negative surplus; integral-differential equation

中图分类号:O211.6

文献标志码:ADOI:10.3969/j.issn.1000-2375.2016.01.004

文章编号:1000-2375(2016)01-0018-07

通信作者

作者简介:贺小丽(1994-)，女，本科生；余国胜,, 讲师，E-mail:guosyujianghanun@126.com

基金项目:江汉大学科研启动项目(2011021)资助

收稿日期:2015-07-22