混合序列下半参数模型估计的相合性

许雪

(湖北大学数学与统计学学院,湖北 武汉 430062)



许雪

(湖北大学数学与统计学学院,湖北 武汉 430062)

摘要：研究误差序列为混合序列的半参数回归模型,利用混合序列的Rosenthal型不等式和截尾的方法, 讨论参数β的最小二乘估计量和未知函数g(·)的非参数估计量的强相合性和r阶平均相合性.

关键词：半参数回归模型混合序列;强相合性;r阶平均相合性

0引言

考虑半参数回归模型

yi=xiβ+g(ti)+ei,i=1,2,…,n

(1)

其中ei为随机误差序列,E(ei)=0, {(xi,ti),1≤i≤n}为固定设计点列,β为未知参数,且β∈R,g(·)为紧集D上的未知函数.

(1)式可写成

yi-xiβ=g(ti)+ei,i=1,2,…,n.

若β已知且E(ei)=0, 则g(ti)=E(yi-xiβ), 1≤i≤n, 此时g(·)的非参数估计为

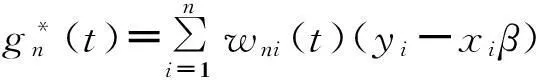
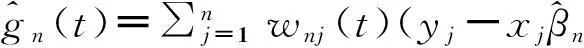
自1989年Engle等[1]在研究气候条件对电力需求影响的问题时提出了半参数回归模型以来,此问题引起了越来越多学者的关注. 它同时包含了参数和非参数分量,相比于一般线性模型而言,更具有灵活性.半参数模型综合了线性模型和非线性模型的优点,更好地描述了现实问题,从而被用于研究许多有意义的问题,比如,基本模型下研究统计量的大样本性质,即运用各种不同的估计方法或在不同的误差设定下,探讨相关估计量的强、弱相合性、r阶平均相合性及其收敛速度等;或把基本模型进行推广,探讨在数据截断或缺失时,模型的估计及估计量的性质.

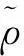
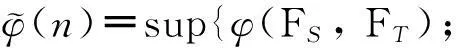
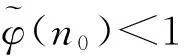
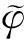
以下给出一些证明定理需要的条件.

条件A1:g(·)是在闭区间上的连续函数且满足1阶Lipschitz条件.

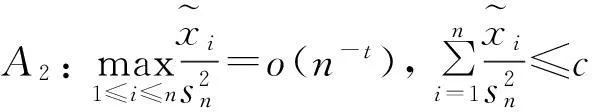
条件A3:

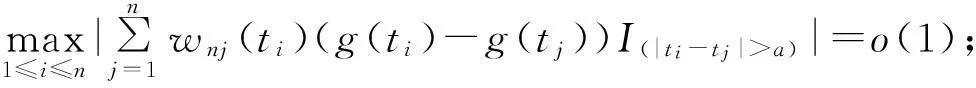
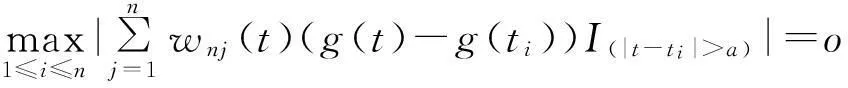
1引理

为了得出本文中的主要结论，本节先给出一些相关的引理.

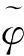
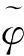
2主要结果及证明

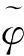
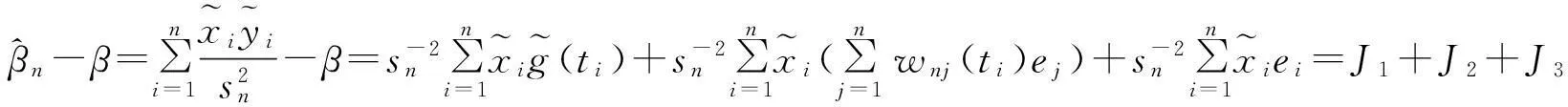
先证

J1→0,n→∞

(2)

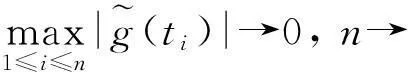
J2→0,n→∞

(3)

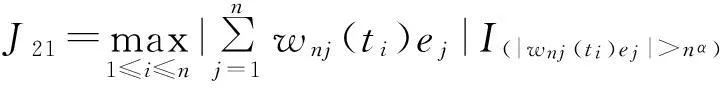
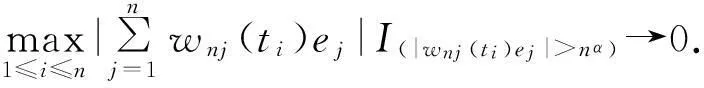
由Borel-Cantelli引理知

(4)

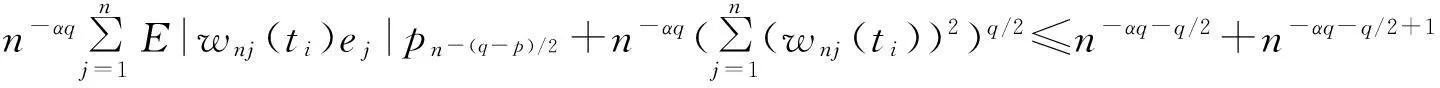
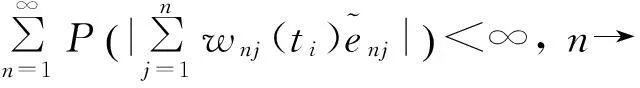
J22→0,n→∞

(5)

再证J23→0, 由Hölder不等式,有

故

J23→0, a.s.

(6)

由(4)～(6)式可得I2→0 a.s..

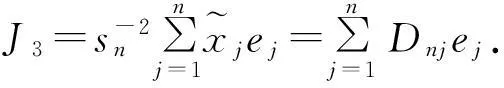
J3→0, a.s.

(7)

综上所述,定理1证明完成.

定理2的证明由定理条件及对所有的t∈D, 有

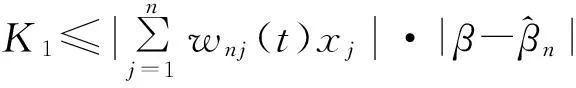
由定理1及定理条件知K1→0,n→∞.

综上所述,定理2证明完成.

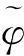
由Cr不等式有

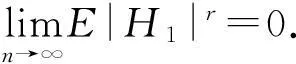
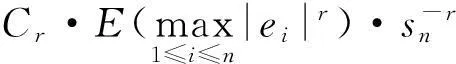
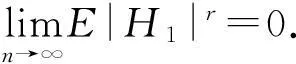
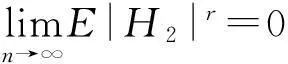
由Minkowski不等式有

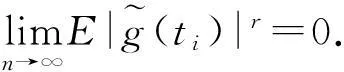
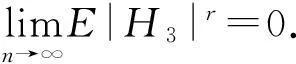
故

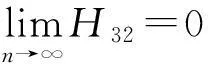
由于

n-δ/α-δ/2→0,n→∞.

故

综上所述,定理3得证.

定理4的证明

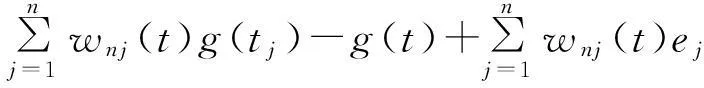
再结合Cr不等式有

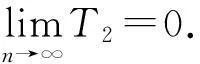
综上所述,定理4得证.

参考文献3

[1] 吴本忠. 混合误差半参数回归模型估计的强相合性[J]. 应用数学, 1998, 11(3): 27-31.

[2] Engle R F, Granger W J, Rice J, et al. Semiparametric estimates of the relation between weather and electricity sales[J]. Journal of the American Statistical Association, 1986, 80: 310-319.

[3] 胡舒合. 固定设计下半参数回归模型估计的强相合性[J]. 数学学报, 1994, 37(3): 393-401.

[4] 任哲,陈明华. NA样本下半参数回归模型估计的强相合性[J]. 高校应用数学学报(A辑), 2000, 15(4): 467-474.

[5] 闫在在, 吴伟志. 半参数回归模型的近邻估计-鞅差误差序列情形[J]. 应用概率统计, 2001, 17(1): 44-51.

[6] 任娜,郭鹏江. 一类混合序列下半参数模型估计的强相合性[J]. 西北大学学报:自然科学版, 2012, 42(1): 17-20.

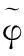
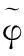
(责任编辑赵燕)

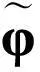
XU Xue

(Faculty of Mathematics and Statistics, Hubei University, Wuhan 430062,China)

Abstract:We studied the semiparametric regression model with -mixing error sequences and discussed its strong consistency and r-th mean consistency of the estimators of β and g(·) by using -mixing sequences’ Rosenthal inequality and trucated method.

Key words:semiparametric regression model; -mixing sequences; strong consistency; r-th mean consistency

中图分类号:O212.2

文献标志码:ADOI:10.3969/j.issn.1000-2375.2016.01.001

文章编号:1000-2375(2016)01-0001-06

作者简介:许雪(1992-),女，硕士生

收稿日期:2015-10-25