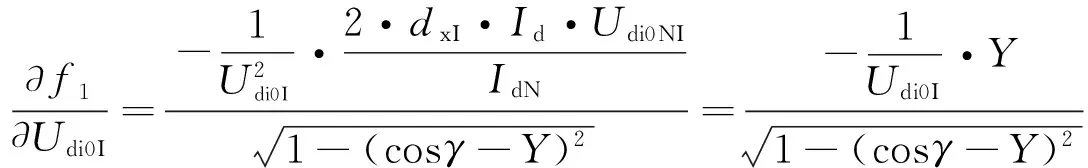特高压直流分层接入工程主回路稳态参数的分析与计算
2016-02-16苗立俐朱坤琳温渤婴
苗立俐,朱坤琳,温渤婴
(1.中国农业大学信息与电气工程学院,北京市 100083; 2.国网北京市电力公司, 北京市 100031)
特高压直流分层接入工程主回路稳态参数的分析与计算
苗立俐1,朱坤琳2,温渤婴1
(1.中国农业大学信息与电气工程学院,北京市 100083; 2.国网北京市电力公司, 北京市 100031)
在高压直流工程规划设计初期,需要对主回路稳态参数进行计算。首先把特高压直流分层接入系统简化为2个单层系统,归纳了单层工程主回路稳态参数计算方法。分析证明了低功率情况下提高换流器无功消耗的2种方法,相应地提出2种无功校验算法。在低功率情况下,分层工程若一个系统由于无功要求需提升直流电流,则会导致各系统无功校验后的直流电流不一致。针对此问题,提出了层间计算的解决方法。取各层系统直流电压的最低值作为层间控制电压,用此电压调整换流器的其他控制参数。调整后关断角、理想空载直流电压和换流器无功消耗的变化规律用Matlab分析给出。最后,用算例进行了稳态运行特性分析,验证了本文提出算法的合理有效性。
特高压直流分层接入工程;低功率;无功校验;层间计算;主回路稳态参数
0 引 言
特高压直流输电系统因传输容量大、电压等级高和传输距离长等优点在我国迅速发展[1]。特高压直流输电分层接入工程是在此基础上进一步创新和发展的,具有系统短路比相对增大,电压支撑能力提升,潮流调节更加灵活等优点[2]。目前在规划建设中的特高压分层接入工程可达到直流电压±1 100 kV,输送功率12 000 MW[3]。可以预见,特高压分层接入工程在未来电网中占据重要的地位。
直流输电系统主回路稳态参数计算的目的是在已知额定理想空载直流电压、分接头档位范围、额定交流电压等系统条件下,计算在各种工况下直流侧和交流侧的运行参数,以初步判断控制角、理想空载直流电压、分接头的运行状况,初步计算各种工况下的无功消耗,继而为无功补偿设备的配备和交流滤波器的设计等后续工作提供参考。文献[4-8]介绍了常规直流输电工程的主回路稳态参数计算方法。但现有文献未针对特高压分层接入工程的稳态参数进行过讨论。文献[9] 通过PSCAD/EMTDC仿真得出,各分层交流系统间无功耦合程度较弱,可以按系统进行滤波器配备和无功平衡。因此本文探索把分层工程拆分为单层工程计算的可行性。
为保证直流电流不发生电流断续,一般要求直流系统传输的有功功率不低于额定值的10%[1]。在直流工程送端机组初始投产时期或送端水电站进行季节性输送功率调节等情况下,直流系统会运行在额定功率0.1 pu起始的较低功率范围内。此时,直流电流较小,换流器的无功消耗也偏小,由于绝对最小滤波器的要求,在不采取措施的情况下直流系统会向交流系统倒送无功功率,这种状态称之为低功率运行。低功率运行时,由于无功要求可能存在一个系统被迫提升直流电流,导致各层系统直流电流不一致的情况,而串联的换流器通过的直流电流是相同的。此时需探讨系统最终将稳定在何种运行状态,以及如何进行此情况下的稳态参数计算。
本文将针对特高压分层接入工程,探讨一种适用于各工况的计算方法,着重讨论低功率情况的层间计算问题,并得到相应的稳态运行参数。
1 分层接入工程的系统结构
特高压直流分层接入工程是指将受端两极的双12脉动换流器经高、低端换流变分别连于不同交流系统接线方式下的直流输电工程[3]。其无功补偿设备也分别接入各交流系统,如图1所示。

图1 特高压直流分层接入方式Fig.1 UHVDC hierarchical connection mode
将分层系统等效为直流电流相同的2个单层系统,如图2、3所示。2个单层等效系统的直流线路电阻和接地电阻各占分层系统的一半。

图2 系统AFig.2 System A
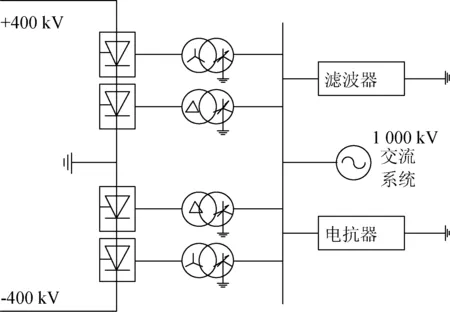
图3 系统BFig.3 System B
分层工程的稳态参数计算可以对各层系统分别进行,本文称其为稳态参数常规计算。常规计算时逆变侧各系统的传输功率、直流电压之和等于特高压分层接入工程的总传输功率、总直流电压[10],一般情况下各取一半。
2 稳态参数常规计算
2.1 基本流程
分层接入方式指的是受端分层,本节以逆变侧为例进行阐述,整流侧同理。本文所有下标R代表整流侧,下标I代表逆变侧,下标N代表额定值。需要依次计算以下各稳态参数[4-8]:
Id=PdR/UdR
(1)
式中 :Id为直流电流,kA;PdR为整流侧单极传输有功功率, MW;UdR为整流侧直流电压, kV。
PdI=PdR-Id2·Rd
(2)
式中:PdI为逆变侧单极传输有功功率, MW;Rd为单极直流线路电阻, Ω。
UdI=PdI/Id
(3)
式中UdI为逆变侧直流电压, kV。
(4)
式中:Udi0I为逆变侧理想空载直流电压, kV;n为UdI对应的6脉动换流器个数;dxI为换流器相对感性压降;drI为换流器相对阻性压降;IdN为额定直流电流,kA;Udi0NI为额定理想空载直流电压, kV ;UTI为换流器正向导通压降, kV;γ为关断角,rad。
(5)
式中μI为换相角,rad。
换流器总是充当交流系统的无功负荷,12脉动换流器消耗的无功功率QdcI满足关系:
(6)
进行完初步计算之后需进行无功校验。
2.2 无功校验的必要性
无功控制的目的在于保证
ΔQ=Qf-Qr-Qdc-Qac=0
(7)
式中:ΔQ为交直流系统无功不平衡量,Mvar;Qf为投入滤波器电容器的无功总量,Mvar;Qr为投入电抗器的无功总量,Mvar;Qac为交流系统吸收的无功功率,Mvar。
高压直流输电系统进行无功控制时,在无功不平衡量不为0时,首先考虑的是投切无功补偿设备进行无功补偿[11]。在直流系统运行时,由于滤波要求,如式(8),有绝对最小滤波器容量Qfmin的限制[12-13],Qf≥Qfmin;交流系统无功吸收能力有限,Qac≤Qacmax;一般在直流系统可以进行提高无功消耗的情况下尽量不配备电抗器[14],系统配备电抗器的总容量记为Qrmax,有Qr≤Qrmax。所以要求Qdc≥Qdcmin,以维持系统的无功平衡[15],Qdcmin为换流器最小无功消耗。
Qdcmin=Qfmin-Qrmax-Qacmax
(8)
2.3 提高换流器无功消耗的方法
低功率运行时因直流电流较小,换流器无功消耗Qdc一般偏小,此时需要研究提高Qdc的方法。
由式(6)可知,QdcI和Udi0I、Id、γ、μI都有关,为简化分析,在定功率控制的情况下,分Id不变和Id改变2种情况讨论。
2.3.1 调节控制角和分接头档位
在直流工程运行过程中一般应保证系统的传输直流电压,因此在分接头有调节能力时优先进行分接头调整,此时Id不变。
现有文献一般靠提高Id来提高QdcI[15-16]。本文提出在Id不变情况下,提高Udi0I和γ也可以提高QdcI。证明过程见附录A。
由于分接头档位数和设备耐压参数的限制,理想空载直流电压Udi0有限值[Udi0 min,Udi0 max],此方法提升无功消耗能力有限。当Udi0碰上限时,由于式(4)的约束,无法继续通过提高γ来提高QdcI。若此时换流器无功消耗仍不足,需提高Id来进一步提高QdcI。
2.3.2 调节控制角和直流电流
文献[15]证明了当Id增大,γ增大,Udi0I不变时QdcI会大幅度增大,本文不再赘述。
综上,常用的提高QdcI的组合为:(1)Id不变,增大γ和Udi0;(2)Udi0不变,增大γ和Id。
通常为保证直流电压一定,在分接头有调节能力时优先选用方式(1)提高换流器的无功消耗,当Udi0碰上限时改用方式(2)。
2.4 无功校验的算法
若式(6)计算出的QdcI小于式(8)的Qdcmin,则保持原来的UdI,令QdcI=Qdcmin。利用牛顿拉夫逊法求解方程组(9)[8],重新计算Udi0I、γ、μI。状态变量X1=(Udi0IγμI)T。
(9)
若计算结果的Udi0I在范围内,则无功校验结束。此时对应方式(1)。
若计算结果的Udi0I不在范围内,则令QdcI=Qdcmin,Udi0I为Udi0I的限值,提高Id,重新计算。状态变量X2=(UdIγμI)T。此时对应方式(2)。
至此无功校验结束,稳态参数常规计算完成。
3 稳态参数层间计算
3.1 层间计算的必要性
图1—3所示分层工程各层系统进行常规计算时会出现表1所示的4种情况。当出现情况2、3、4时改用方式(2),单独考虑2个受端系统,常规计算后各层系统的直流电流会被迫调整为不相同,而串联的换流器直流电流相等,一个系统由于无功控制使直流电流发生改变将影响到另一个换流器的运行参数。此时需要探究系统最终将稳定在何种状态。本文提出此种情况下需进行层间计算。
表1 各系统常规计算时Udi0的碰限状况
Table 1Udi0condition under each general calculation

3.2 层间计算方法
层间计算和常规计算的思路基本相同,主要在于如何进行层间调控保证各层系统直流电流Id相等。传输至受端2个系统的有功功率相同时,Id相等意味着2个换流器的直流电压Ud相同。
(1)确定层间控制电压Ud_c
由2.3节反推,若层间控制电压Ud_c大于换流器的常规控制电压Ud_g,则会计算出换流器无功消耗不足的结果。所以,取各层系统中常规计算的最低直流电压作为Ud_c。
(2)确定需要调整参数的换流器m
若该换流器的Ud_g=Ud_c,则不再调整;若该换流器的Ud_g>Ud_c,则此换流器需要调整参数。对应表1情况2时m为B,情况3时m为A。
(3)计算换流器m的控制参数
根据常规计算未进行方式(1)和方式(2)调整时是否满足Qdc≥Qdcmin的要求,分2种情况。
1)Qdc≥Qdcmin
这类情况下,常规计算有γ=γN。降压工况γ会大于γN,但降压工况不会出现Udi0I碰上限的状况,故不会进入到层间计算环节。所以,若进入到层间计算环节,并满足Qdcmin的要求,则有γ=γN。
用Ud_c、Pd_m和γN按式(4)—(6)重新计算换流器m的各控制参数。其中,Pd_m为换流器m传输的有功功率,Udi0_m、γ_m、μ_m、Qdc_m类似。
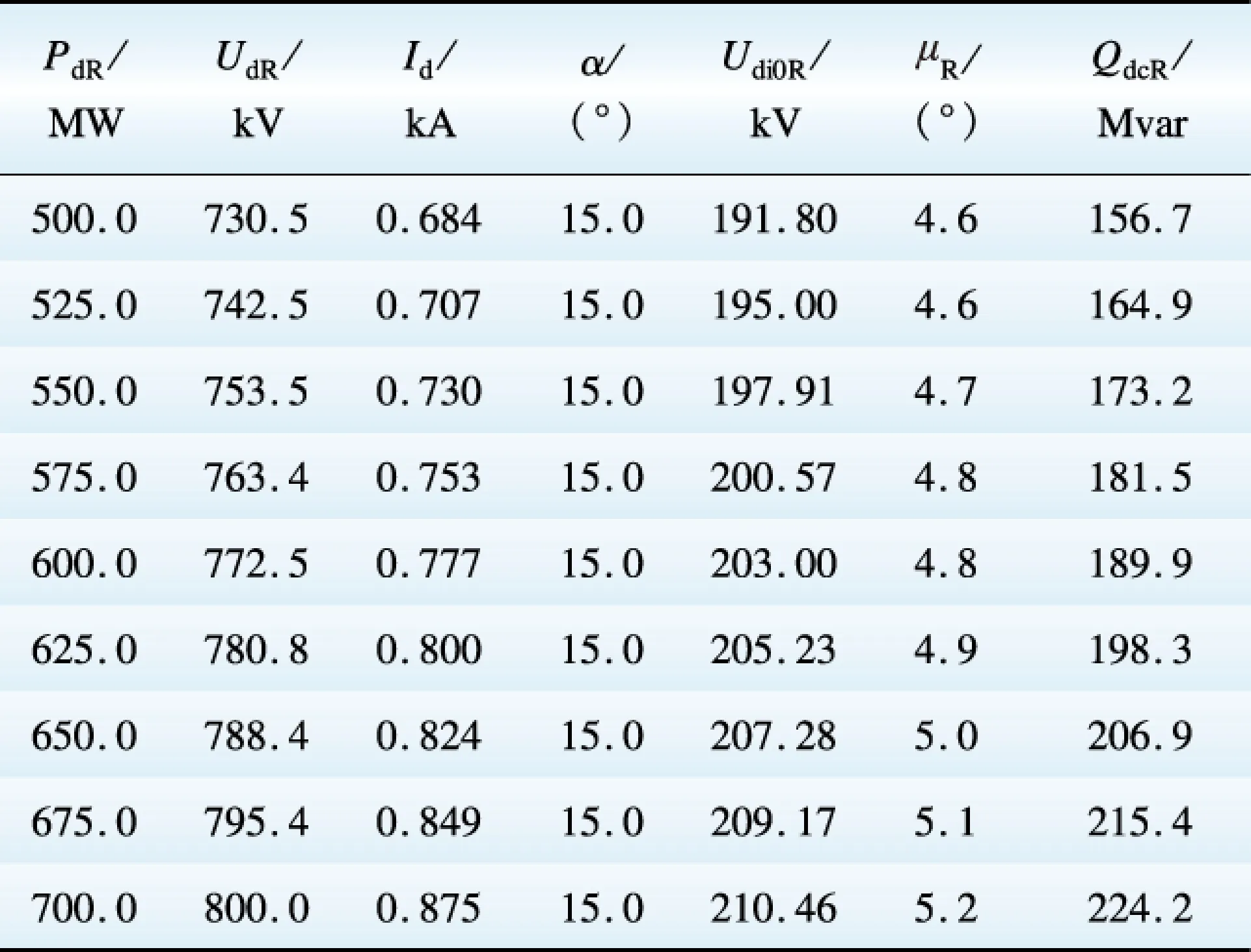
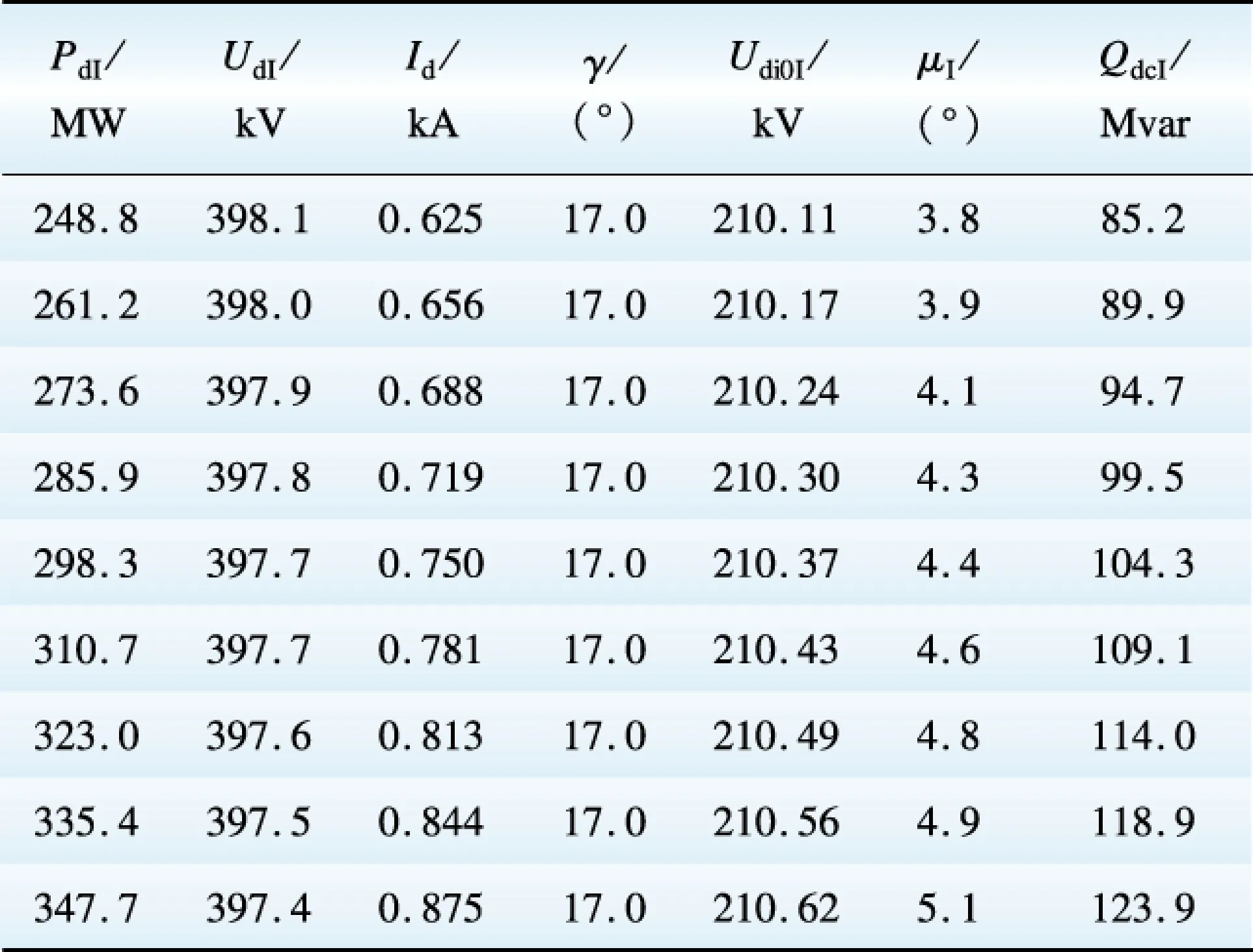
2)Qdc 用Ud_c、Pd_m和Qdcmin以牛顿拉夫逊法按方程组(9)重新调整此换流器的各控制参数。 各情况下的确定量和待定量如表2所示。 3.3 层间计算后参数变化规律 (1)有功功率PdI 表2 层间计算的确定量和待定量 Table 2 Constants and variables under calculation between layers (2)换流器参数γ、Udi0I、QdcI 下面讨论层间计算后换流器m的参数变化规律,即分析定功率情况下降低直流电压的影响。按常规计算未进行方式1和方式2调整时是否满足Qdc≥Qdcmin的要求,分2种情况。 1)Qdc≥Qdcmin 由前面分析可知,此种情况下,常规计算有γ=γN。此时UdI下降,γ不变,根据式(4),因Udi0I主要受UdI的影响,Id作用在相对感性压降部分影响很小,所以Udi0I降低。Udi0I降低后若没有碰到最低限值,则层间计算后γ=γN,否则γ增大。 令特高压分层接入工程单极额定传输功率PdNR=5 000 MW,UdNR=800 kV,Rd=4.658 Ω,dxI=10%,drI=0.3%,UTI=0.3 kV,γ=γN=17°,Udi0NI=223.93 kV。当单极传输功率PdR=500 MW时,Id从0.625 kA增大到0.9 kA,相应的UdI从797.09 kV下降到551.36 kV。用上述数据计算QdcI。在Matlab中绘制QdcI-Id图形,如图4所示。 图4 QdcI随Id变化曲线Fig.4 QdcI-Id curve 可见,当PdR一定,Id增大,γ=γN时,QdcI是上升的,QdcI-Id是近似于线性的非线性关系。当Udi0I降低后碰到下限,γ增大时,QdcI由于γ增大的影响会更加上升。 2)Qdc 仍以前述数据计算,γ调整为[17°, 40°]的范围,计算相应的Udi0I和μI,继而计算出QdcI,如图5所示。 图5 QdcI随Id,γ变化曲线Fig.5 QdcI-Id/γ curve 由图可见,对于任意一个γ,随Id增大,QdcI都是增大的;对任意一个Id,随γ增大,QdcI也是增大的。层间计算后Id增大,所以,对于相同的QdcI,总有一个较常规计算小的γ满足要求,层间计算后γ减小(由于换流器无功消耗的要求,γ仍比额定控制角大)。可见由于Id增大的影响,提升QdcI至要求值时,γ可以较常规计算时少增大一些。由式(4)可知,UdI和γ均减小,Udi0I也变小。 综上,在定功率控制模式下,层间计算后被调整的换流器参数较常规计算变化如下:PdI、UdI、Udi0I均下降,若常规计算不需提高Qdc,则QdcI上升,γ不变或增大;若常规计算需采取措施提高Qdc,则QdcI不变,γ降低。 4.1 稳态参数计算 模拟工程单极PdNR=5 000 MW,额定直流电压UdNR=800 kV,单极大地工况电阻(直流线路电阻与接地电阻之和)Rd=6 Ω,额定触发角αN=15°,额定关断角γN=17°。系统参数见表3。整流侧两换流器相同,各交流系统的绝对最小滤波器个数均为2,各换流器dr=0.3%,UT=0.3 kV。 按2.1节中的方法进行单极大地全压正送工况计算,结果如图6—8所示。各图左下部分有递增趋势的曲线代表μ,有与横轴平行趋势的线代表控制角α/γ。各图右下部分曲线代表Qdc,曲线下方的折线代表滤波器投入(电抗器切除)过程,曲线下方折线代表滤波器切除(电抗器投入)过程。低功率部分的计算结果见附表1—4,经验证符合方程组(9)。 表3 模拟工程系统参数 Table 3 System parameters of simulated engineering 图6 整流器Fig.6 Rectifier 图7 接500 kV系统的逆变器Fig.7 Inverter to 500 kV system 4.2 稳态参数分析 由图7、图9低功率部分可知,接500 kV系统逆变器的Qdcmin为: (245×2-60×2-190)Mvar=180 Mvar。为满足Qdcmin的要求,此换流器采用了增大γ,降低UdI的措施。而接1 000 kV系统的逆变器的Qdcmin为(350×2-240×2-286) Mvar=-66 Mvar,在常规计算时满足Qdc≥Qdcmin的要求,不需进行方式(1)和方式(2)的调整。 但此时接2个系统的逆变器计算出的直流电压、直流电流不同,需进行层间计算。因接500 kV系统逆变器的降压情况较为严重,调整接1 000 kV系统的逆变器直流电压至与前者相同。图9所示过程在实际运行中不会稳定存在,只是计算过程的一个中间步骤。 图8 接1 000 kV系统的逆变器Fig.8 Inverter to 1 000 kV system 在层间计算中,用确定的传输功率和层间控制电压重新计算接1 000 kV系统逆变器的其他控制参数,最终稳定在图8状态。由附表3和附表4的数据可知,调整后受端系统传输有功功率PdI变化量仅为0.2 MW左右,不会对有功功率传输的稳定性造成较大影响,符合3.3节(1)的分析。从图8和图9的对比可以看出,层间计算后UdI下降,Udi0I下降,并且由于分接头档位限制Udi0I碰下限,γ上升,QdcI上升,与3.3节(2)中1)的分析一致。由附表3和附表4可以看出调整后的换流器各参数仍在合理范围内,不会造成逆变器继发换相失败等严重问题。 图9 接1 000 kV系统的逆变器(层间计算前)Fig.9 Inverter to 1000 kV system (before the layers calculation) 4.3 方法评价 此方法解决了特高压直流分层接入工程主回路稳态参数常规计算后各层系统直流电流不一致的问题。经层间计算后,常规计算不需降压的换流器被迫降压,会引发控制角增大,产生谐波增加[17],无功消耗增加等问题。但对于分层系统而言,各层系统的条件不一致,导致运行状态不一致属正常现象。此方法综合考虑了有功功率传输的稳定性和无功功率不平衡量对交流电压的影响,在滤波器、电抗器等无功补偿设备配置合适的情况下,可得到各运行参数在控制范围内的合理结果,符合电网安全稳定运行的要求。 本文给出了特高压直流分层接入工程的主回路稳态参数计算的完整方法:把分层工程拆分为2个单层工程分别进行常规计算,若无功校验进入到方式(2),则继续进行层间计算。通过对实例分析,说明了计算方法合理有效,对实际工程的前期设计具有一定指导意义。得出的主要结论如下。 (1)2种无功校验的算法对应2种提高换流器无功消耗的方式。方式(1)为调节控制角和换流变分接头,方式(2)为调节控制角和直流电流。在分接头有调节能力时优先进行方式(1)控制,否则转为方式(2)。在低功率运行时,常规计算进入方式(2)后需进行层间计算。 (2)层间计算时,控制电压应取常规计算各层系统电压的最低值。常规控制电压不等于层间控制电压的换流器需按层间控制电压和确定的传输功率重新调整参数。 (3)层间计算后,换流器较常规计算的变化为:PdI、UdI、Udi0I均下降,若常规计算满足QdcminI的要求,则QdcI上升,γ不变或增大;若常规计算需采取措施提高无功消耗,则QdcI不变,γ降低。 [1]赵畹君.高压直流输电工程技术[M].北京:中国电力出版社, 2004:18-29. [2]高媛, 韩民晓. 特高压直流输电多端馈入方式稳态特性研究[J]. 电网技术, 2014, 38(12) :3447-3453. GAO Yuan, HAN Minxiao, Steady State Characteristic of Multi Infeed UHVDC Power Transmission[J]. Power System Technology, 2014, 38(12): 3447-3453. [3]刘振亚, 秦晓辉, 赵良,等. 特高压直流分层接入方式在多馈入直流电网的应用研究[J]. 中国电机工程学报, 2013, 33(10) :1-7. LIU Zhenya, QIN Xiaohui, ZHAO Liang, et al. Study on the application of UHVDC hierarchical connection mode to multi-infeed HVDC system[J]. Proceedings of the CSEE, 2013, 33(10) :1-7. [4]王峰. 高压直流输电系统基本设计若干问题研究[D]. 杭州:浙江大学, 2011. WANG Feng. Research on several issues in HVDC transmission design[D]. Hangzhou: Zhejiang University, 2011. [5]邓旭, 王东举, 沈扬,等. ±1 100 kV准东—四川特高压直流输电工程主回路参数设计[J]. 电力自动化设备, 2014, 34(4):133-140. DENG Xu, WANG Dongju, SHEN Yang, et al. Main circuit parameter design of Zhundong—Sichuan ±1 100 kV UHVDC power transmission project[J]. Electric Power Automation Equipment, 2014, 34(4):133-140. [6]张相宇, 温渤婴, 李鹏. 高压直流输电系统主回路参数计算平台的研发[J]. 电力建设, 2014, 35(2): 52-56. ZHANG Xiangyu, WEN Boying, LI Peng. Research and development of computing platform for main circuit parameters in HVDC power system[J]. Electric Power Construction, 2014, 35(2): 52-56. [7]陈锡磊, 周浩, 沈扬,等. 溪洛渡—浙西±800 kV /7 500 MW特高压直流输电工程主回路参数设计[J]. 电网技术, 2011,35(12):26-32. CHEN Xilei, ZHOU Hao, SHEN Yang, et al. Study and design of main circuit parameters for ±800 kV /7 500 MW DC power transmission project from Xiluodu to Zhexi[J]. Power System Technology, 2011, 35(12):26-32. [8]王峰, 徐政, 黄莹,等. 高压直流输电主回路稳态参数计算[J]. 电工技术学报, 2009, 24(5):135-140. WANG Feng, XU Zheng, HUANG Ying, et al. Calculation of main circuit parameters for HVDC transmission[J]. Transactions of China Electrotechnical Society, 2009, 24(5): 135-140. [9]李少华,王秀丽,张望,等. 特高压直流分层接入交流电网方式下直流控制系统设计[J]. 中国电机工程学报, 2015, 35(10): 2409-2416. LI Shaohua, WANG Xiuli, ZHANG Wang, et al. Control system design for UHVDC hierarchical connection to AC grid[J]. Proceedings of the CSEE, 2015, 35(10): 2409-2416. [10]郭龙,刘崇茹,贠飞龙,等.±1 100 kV直流系统分层接入方式下的功率协调控制[J].电力系统自动化,2015,39(11):24-30. GUO Long, LIU Chongru, YUN Feilong, et al. Power coordination control of ±1 100 kV UHVDC system with hierarchical connection Mode[J]. Automation of Electric Power Systems,2015,39(11):24-30. [11]朱坤琳, 温渤婴. 高压直流输电系统的无功功率平衡和控制方法[J]. 电力建设, 2015, 36(9):35-42. ZHU Kunlin, WEN Boying. Reactive power balance and control methods in HVDC transmission system[J]. Electric Power Construction, 2015, 36(9): 35-42. [12]戴国安, 周君文, 王亚非. 特高压直流无功控制策略研究[J]. 电力系统保护与控制, 2008, 36(14):48-51. DAI Guoan, ZHOU Junwen, WANG Yafei. Strategy of reactive power control on UHVDC[J]. Power System Protection and Control, 2008, 36 (14):48-51. [13]张望, 郝俊芳, 曹森,等. 直流输电换流站无功功率控制功能设计[J]. 电力系统保护与控制, 2009, 37(14):72-76. ZHANG Wang, HAO Junfang, CAO Sen, et al. Design of reactive power control for HVDC converter station[J]. Power System Protection and Control, 2009, 37(14):72-76. [14]杨志栋, 殷威扬, 李亚男. 三沪直流工程无功补偿和控制方案[J]. 电力建设, 2007, 28(12):10-13. YANG Zhidong, YIN Weiyang, LI Yanan. Reactive power compensation and control scheme for the Three Gorges to Shanghai DC project[J]. Electric Power Construction, 2007, 28(12):10-13. [15]张啸虎, 曹国云, 陈陈. 高压直流系统低功率运行时的无功控制策略[J]. 电网技术, 2012, 36(1):118-122. ZHANG Xiaohu, CAO Guoyun, CHEN Chen. Proposal on reactive power control of HVDC system during low power transmission[J]. Power System Technology, 2012, 36(1):118-122. [16]肖鸣, 傅闯, 梁志飞. 高压直流低负荷无功优化功能运行分析[J]. 电力系统自动化, 2010, 34(15):91-95. XIAO Ming, FU Chuang, LIANG Zhifei. An operation analysis of HVDC low load reactive power optimization function[J]. Automation of Electric Power Systems, 2010, 34(15):91-95. [17]王永旭, 温渤婴. 高压直流输电交流滤波器与交流系统最大并联阻抗的分析与计算[J]. 中国电机工程学报, 2015, 35(11): 2703-2710. WANG Yongxu, WEN Boying. Computation and analysis of maximum parallel impedance between the AC filter and AC network in HVDC transmission system[J]. Proceedings of the CSEE, 2015, 35(11): 2703-2710. (编辑 刘文莹) 附录A PdR、Id不变时,由式(2)得PdI不变,由式(3)得UdI不变。由式(4)知,当UdI不变时,提高γ,Udi0I也得到提升。 QdcI和PdI的关系满足式(A1)。 QdcI=PdI·tanφI (A1) 其中φI为功率因数角(°),满足式(A2)[1]。 (A2) 式(A2)记为f3(φI)=cosφI=f2(γ,μI),则 (A3) 由式(A1)、(A3)可知,γ增大,QdcI增大。 附录B 表B1 整流器 Table B1 Rectifier Analysis and Calculation of Main Circuit Steady-State Parameters of UHVDC Transmission System with Hierarchical Connection Mode MIAO Lili1, ZHU Kunlin2, WEN Boying1 (1.College of Information and Electrical Engineering, China Agricultural University, Beijing 10083, China;2.State Grid Beijing Electric Power Company, Beijing 100031, China) It is necessary to calculate the main circuit steady-state parameters at the beginning of the planning and design of HVDC projects. Firstly, this paper simplifies UHVDC transmission system with hierarchical connection mode into two single-layer systems, and concludes the method of main circuit steady-state parameters calculation for single-layer system. Then we analyze two ways to increase the reactive power of converters during low power transmission and present the corresponding reactive power validations. If the DC current increases due to its reactive power requirement in one system, the DC current through the hierarchical systems after reactive power validation will be different in low power condition. Aiming at this problem, we propose calculation between layers as a solution. The lowest DC voltage across the converters of hierarchical systems is selected to be the control voltage between layers, the other control parameters of the converters are adjusted according to this voltage. We analyze the changing characteristics of extinction angle, ideal no-load DC voltage, as well as the reactive power consumption of converter after adjustment with using Matlab. At last, we analyze the steady-state operating characteristics with an example, while verifying the reasonability and effectiveness of the proposed algorithm. UHVDC transmission system with hierarchical connection mode; low power transmission; reactive power validation; calculation between layers; main circuit steady-state parameters 表B2 接500 kV系统的逆变器Table B2 Inverter to 500 kV system 表B3 接1 000 kV系统的逆变器Table B3 Inverter to 1 000 kV system 表B4 接1 000 kV系统的逆变器(层间计算前)Table B4 Inverter to 1 000 kV system (before calculation between layers) TM 72 A 1000-7229(2016)02-0091-09 10.3969/j.issn.1000-7229.2016.02.013 2015-12-10 苗立俐(1992),女,硕士研究生,从事高压直流输电工程稳态运行的潮流分析及无功控制的研究工作; 朱坤琳(1991),女,硕士,从事高压直流输电工程稳态运行的潮流分析及无功控制的研究工作; 温渤婴(1958),男,教授,博士生导师,通信作者,研究方向为高压直流输电技术与继电保护等。



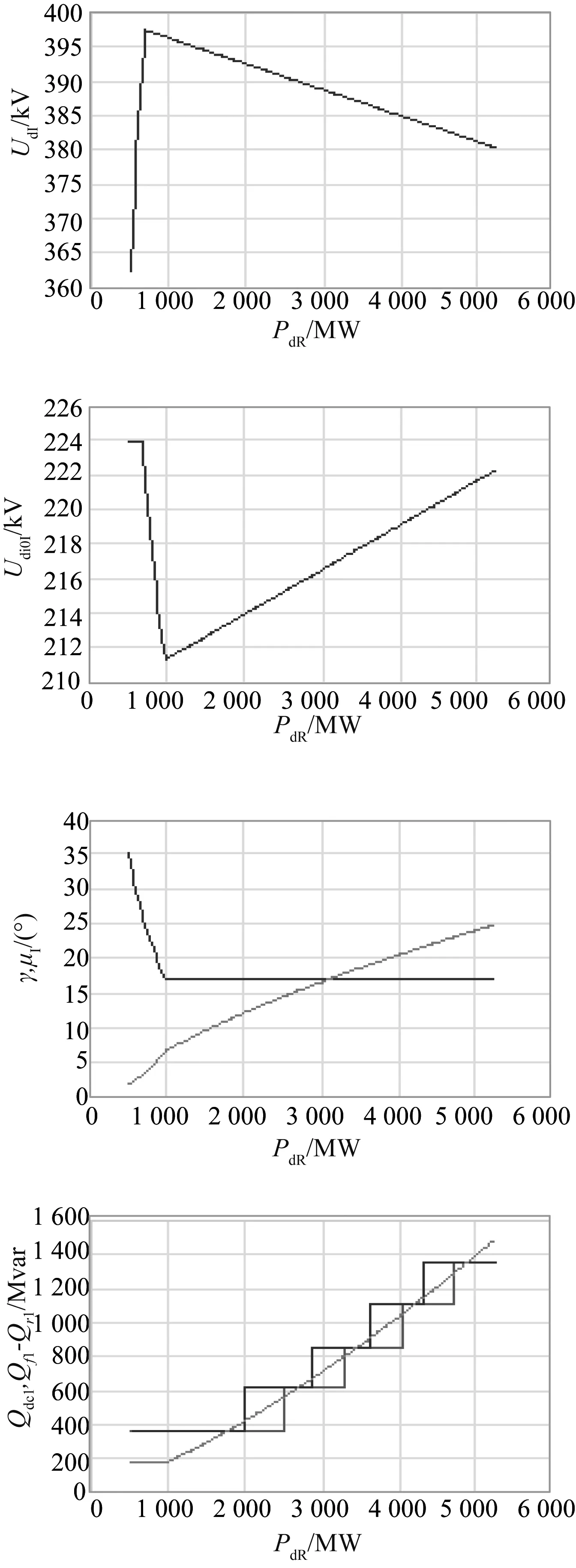
4 实例分析




5 结 论