右逆相干态与单原子作用的量子态保真度

张康隆，陶 宇，刘堂昆

（1．湖北工程职业学院，湖北黄石 435004；2．湖北师范大学物理与电子科学学院，湖北黄石 435002）

右逆相干态与单原子作用的量子态保真度

张康隆1，2，陶 宇2，刘堂昆2

（1．湖北工程职业学院，湖北黄石 435004；2．湖北师范大学物理与电子科学学院，湖北黄石 435002）

运用全量子化理论和数值处理方法，研究了右逆相干态与单原子相互作用的量子态保真度的时间演化特性，讨论了不同的参量对体系的量子态保真度的影响。结果表明：系统、光场和原子三者的保真度始终处在失真状态，而且演化过程无规则。

右逆相干态；单原子；量子态；保真度

0 引言

量子光学的一个重要课题是量子态工程，目的是寻找光场的新量子态并研究其非经典特性，以便更好地了解新的光场本性。利用玻色产生、湮灭算符及与之对应的逆算符作用于不同的光场量子态上可以获得新的光场量子态。例如，文献［1～2］通过玻色产生算符a＋作用于通常的奇偶相干态获得了新的量子态；文献［3］通过玻色产生算符a＋作用于SUq（1，1）奇偶q相干态获得了增加光子SUq（1，1）奇偶q相干态；文献［4］通过玻色产生算符a＋作用于相干态m次获得了增加光子相干态（又称为激发相干态）；文献［5］通过玻色湮灭算符的逆算符a－1作用于通常的奇偶相干态获得了增、减光子奇偶相干态；文献［6］通过玻色湮灭算符的逆算符a－1作用于相干态m次获得了相干态的激发态；文献［7］通过玻色算符的逆算符的组合作用于Fock态上获得了新的光场量子态；等等。以上通过不同的方法所得到的新的光场量子态有不同于原先光场量子态的特性，从而提高了人们制备或者寻找新的光场量子态的兴趣和能力。大家知道量子态是量子信息的载体，量子信息与量子计算机的运行涉及到量子态的传输问题，而量子态的传输必然要考虑保真度的问题。近些年来，保真度概念被一些学者用到量子光学领域［8－12］。本文利用文献［6］获得的新的光场量子态，我们称其为“右逆相干态”，（只是为了避免文献［4］的“激发相干态”和文献［6］的“相干态的激发态”名称上的混淆），研究了右逆相干态与单原子相互作用的量子态保真度的时间演化特性。

1 右逆相干态与单原子相互作用

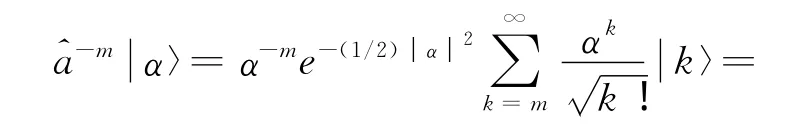
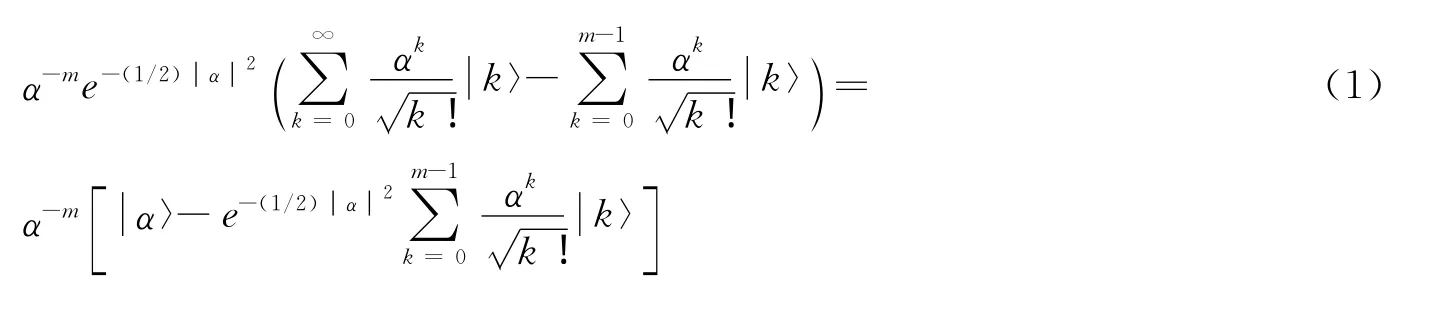
这个态中缺少了k＝0，1，2，…，m－1这些数态。为了区分文献［4］和［6］的两个定义的雷同，我们将

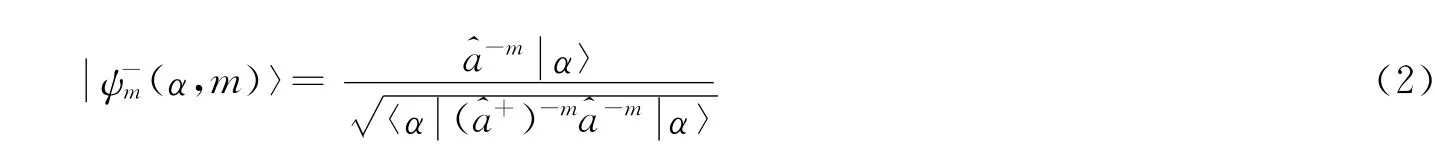
称为“右逆相干态”。归一化后，有

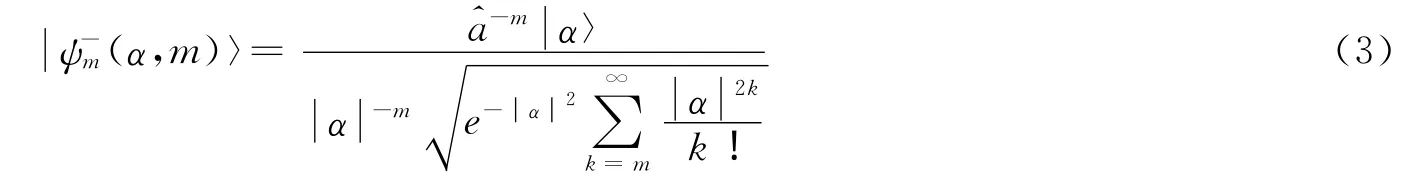
现在，我们考虑量子系统是由右逆相干态与一个二能级原子组成，其相互作用哈密顿量可表示为（ħ＝1）

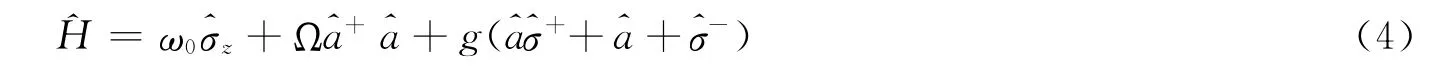
为了方便起见，考虑共振情况（ω0＝Ω）。假设在初始时刻，原子处于基态 g〉和激发态e〉的叠加态

光场处于右逆相干态。则原子和光场的复合系统初始时刻处于态：

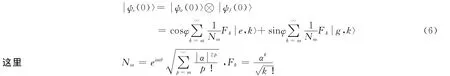
随着时间的演化，在相互作用表象中，系统在t＞0的任意时刻的态矢量为

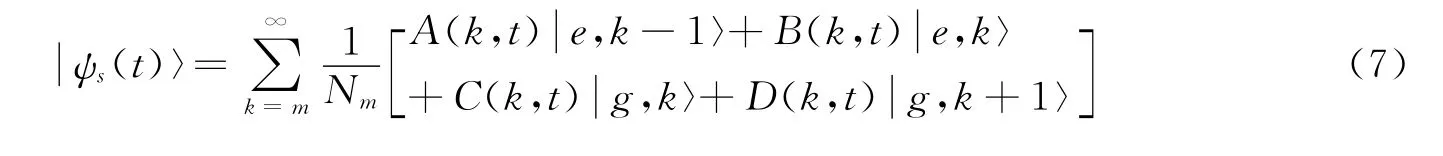
根据薛定谔方程以及初始条件，则可得在共振条件下的各系数为

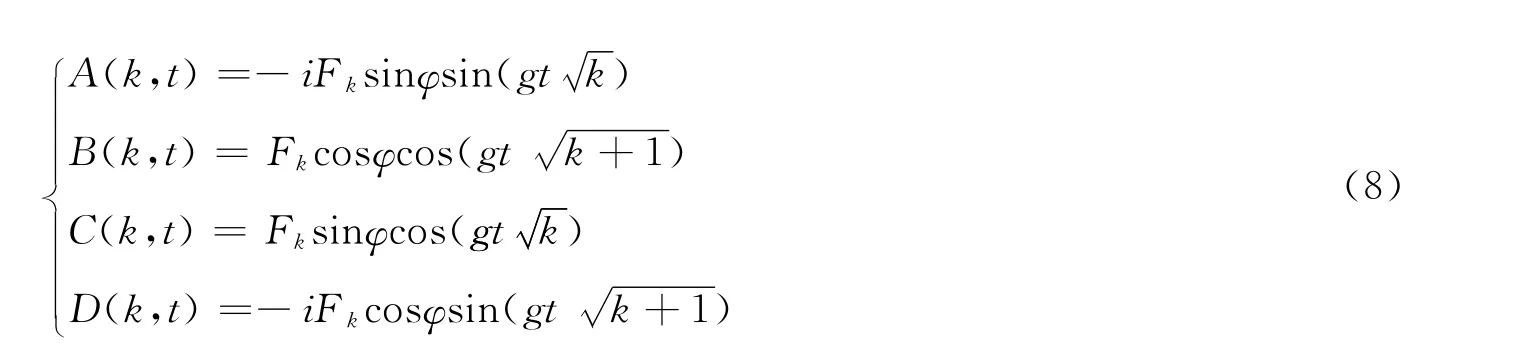
2 量子态保真度的演化

为了描述量子态在传播过程中初态和末态的偏差程度，人们引入了保真度的概念［8～10］，其定义为

其中ρ1和ρ2为两种态所对应的态密度算符，F（ρ1，ρ2）取值范围在0－1之间。当F（ρ1，ρ2）＝0时，表示信息在传播过程中完全失真，即表明初态和末态相互正交；而当F（ρ1，ρ2）＝1时，表示为理想信息传输过程，即表明初态和末态相同。一般情况下，0≤F（ρ1，ρ2）≤1，表示信息在传播过程中存在失真现象。

由以上表示式，容易得到系统、光场和原子的量子态保真度表达式为：

从（10）～（12）式中可以看出，系统、光场和原子的量子态保真度不仅与“时间”gt参量有关，还与参量m、φ以及有关。因此利用数值处理方法，选取不同参量，考察系统、光场和原子的量子态保真度随“时间”gt的演化规律。

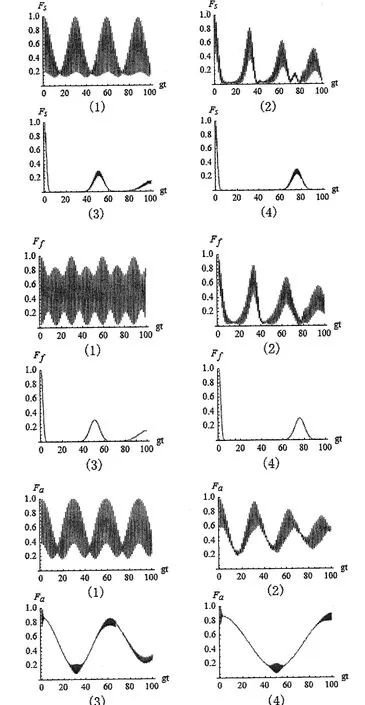
图1 当φ＝π／3，m＝5时，保真度随时间演化曲线。

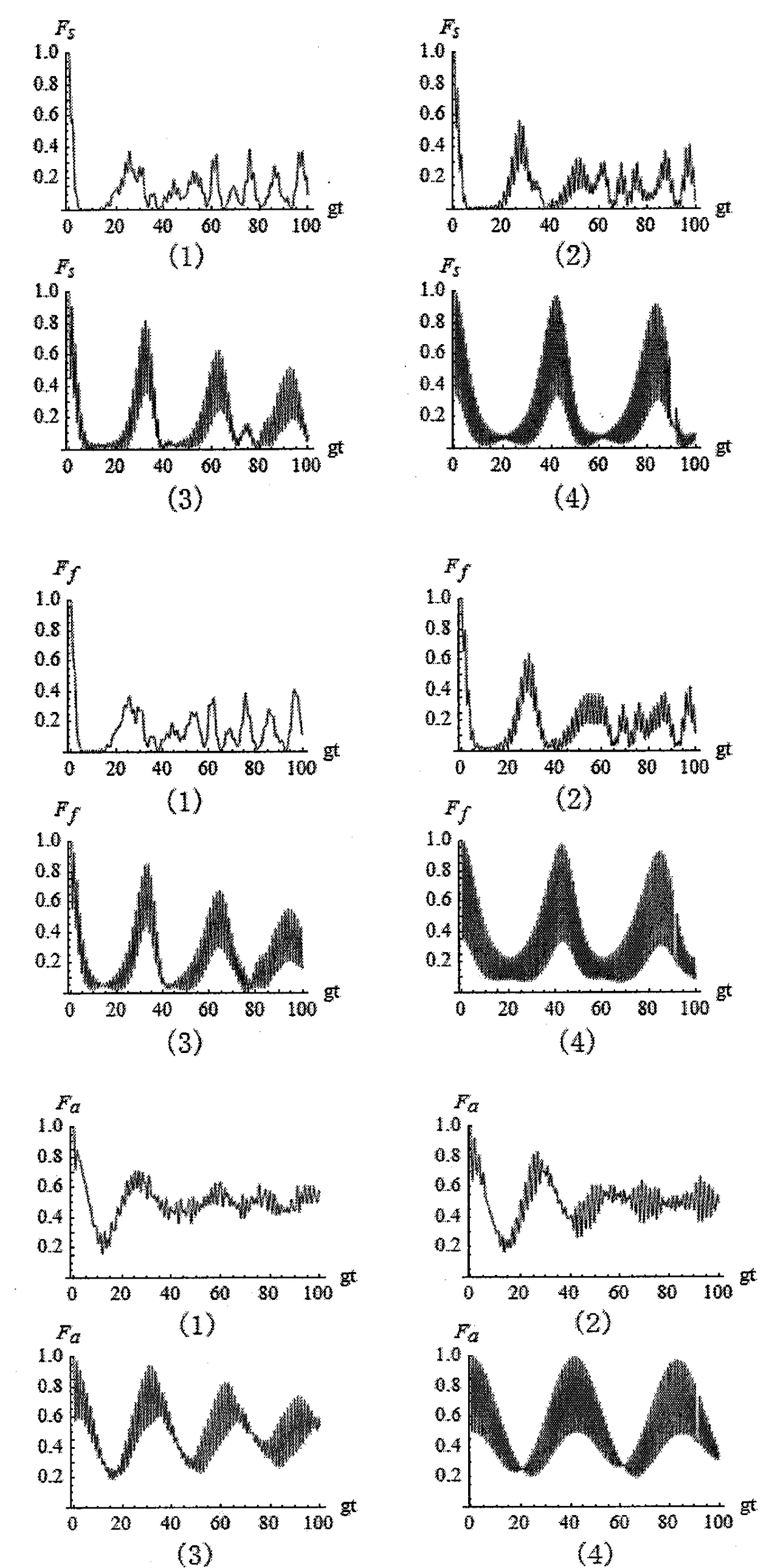
图2 当φ＝π／3，＝2时，保真度随时间演化曲线。

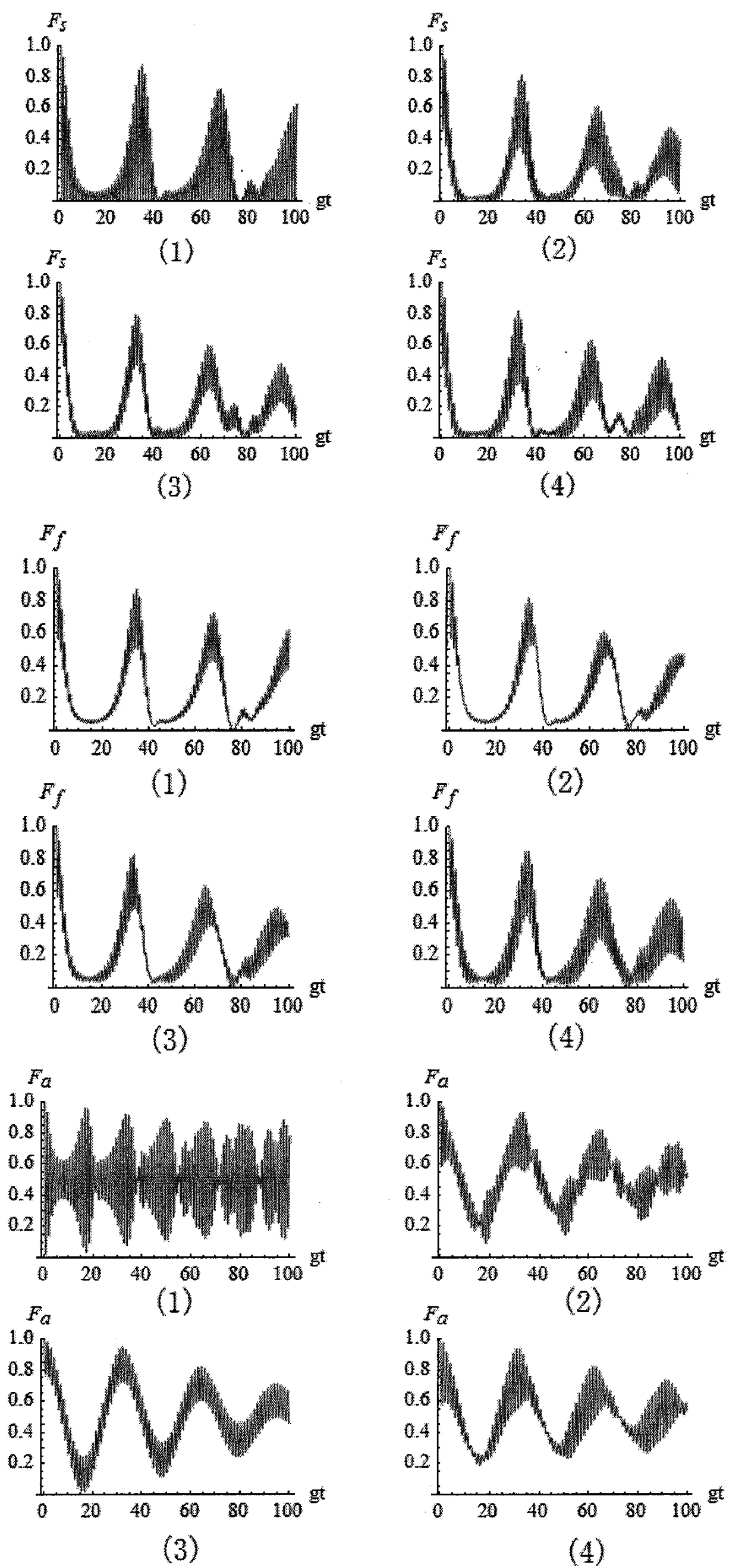
图3 当φ＝π／3，＝2时，保真度随时间演化曲线。

经过数值处理，我们从图1中可以看出：当概率幅角φ和作用次数m一定时，较大的光场强度，使得系统和光场的保真度明显的呈现完全失真现象，而原子的保真度不呈现完全失真现象。从图2和图3中看出：当光场强度一定时，不同的概率幅角φ和作用次数m，系统、光场和原子三者的保真度出现失真现象。另外，从3幅图中可以看出，不管概率幅角φ、作用次数m和光场强度α 取值大小，系统、光场和原子三者的保真度始终处在失真状态，而且演化过程无规则。

3 结论

［1］Dodonov V V，Korennoy Y A，Man’ko V I，et al．Non－classical properties of states generated by the excitations of even／odd coherent states of light［J］．Quantum Semiclass Opt，1996，8：413～427．

［2］Xin Z Z，Duan Y B，Zhang W，et al．Excited even and odd coherent states of the radiation field［J］．J Phys B：At Mol Opt Phys，1996，29：2597～2606．

［3］张 敏，江俊勤．增加光子奇偶相干态的高阶压缩效应［J］．光子学报，2002，31（12）：1436～1438．

［4］Agarwal G S，Tara K．Nonclassical properties of states generated by the excitations on a coherent state［J］．Phys Rev A，1991，43（1）：492～497．

［5］杨庆怡，韦联福，丁良恩．玻色算符的逆算符及其相关的奇偶相干态［J］．物理学报，2003，52（6）：1390～1395．

［6］Wei L F，Wang S J，Jie Q L．Excited states of coherent state and their nonclassical properties［J］．Chin Sci Bull，1997，42（20）：1686～1688．

［7］Nehta C L，Roy A K，Saxena G M．Eigenstates of two－photon annihilation operators［J］．Phys Rev A，1992，46 （3）：1565～1572．

［8］Jozsa R．Fidelity for mixed quantum states［J］．J Mod Opt，1994，41（12）：2315～2323．

［9］刘堂昆，王继锁，柳晓军，等．纠缠态原子与相干光场作用的量子信息保真度［J］．光学学报，2000，20（11）：1449～1455．

［10］刘堂昆，王继锁，柳晓军，等．纠缠态原子偶极间相互作用对量子态保真度的影响［J］．物理学报，2000，49（4）：708 ～712．

Fidelity of quantum state in system of right inverse coherent state interacting with single atom

ZHANG Kang－long1，2，TAO Yu2，LIU Tang－kun2
（1．Hubei Engineering Institute，Huangshi 435004，China；2．College of Physics and Electronic Science，Hubei Normal University，Huangshi 435002，China）

In this paper，the time evolution properties of the fidelity of quantum state in the system of right inverse coherent light field interacting with single atom are studied by means of full quantum theory．The influences of the optical field strength，the probability amplitude angle of the atom and the number of the right inverse operator acting on the coherent states on the fidelity of quantum state are discussed by numerical calculations．The results show that the fidelities of system，optical field and atom are always in a state of distortion，and the evolution has no rule．

right inverse coherent state；single atom；quantum state；fidelity

O431

A

：1009－2714（2016）04－0044－07

10．3969／j．issn．1009－2714．2016．04．011

2016—02—18

国家重点基础研究发展计划项目（2012CB922103），国家自然科学基金（11274104），湖北省自然科学基金（2011CDA021）．

张康隆（1985— ），男，湖北黄冈人，硕士研究生．

刘堂昆，tkliuhs＠163．com