ABC指数与几类点度拓扑指数的关系
2016-02-16甘露
甘 露
(湖北师范大学数学与统计学院,湖北黄石 435002)
GAN Lu
ABC指数与几类点度拓扑指数的关系
甘 露
(湖北师范大学数学与统计学院,湖北黄石 435002)
原子键连通性指数(ABC简称指数)是Eatrada等人在Randic指数的基础上提出的一类拓扑指数。该指数已被证实为研究烷烃的稳定性及环烷烃的应变能等提供了很好的模型。给出了ABC指数和几类点拓扑指数的关系。
ABC指数;点拓扑指数;X指数
0 引言
拓扑指数是从化合物的结构图衍生出来的不变量.近年来,很多拓扑指数是许多数学工作者和化学工作者的主要研究方向,而这些拓扑指数中连通性指数是最为人们所熟知并且有着广泛应用的拓扑指数.然而,许多物质的物理化学性质更多是由分子因子度来决定而不能只看支化度,为了能考虑分子因子度同时还能保持连通性指数的精髓,Estrada[1]在1998年提出了一个新的指数,原子键连通性指数,简称ABC指数.该指数的定义如下:
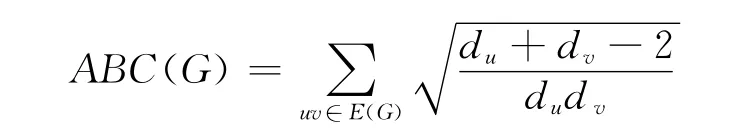
其中E(G)是边的集合,du,dv分别是点u和点v的度。
ABC指数的数学性质在文献[2~4]中已被广泛研究,该指数已被证明在研究烷的热形成中是一个有效的预测性指数,且已被用来研究烷的稳定性以及环烷的应变能等.Zhong[5~6]等人研究了关于R,ABC,X和H及GA指数之间的关系.Al[7]继续了Zhong的工作,又得到了一些点度拓扑指数GA,AZI,R,ABC,H,X之间的关系.本文将进一步研究ABC指数与X,R指数之间的关系.
1 概念及引理
本节将给出几个涉及到的概念和引理.首先给出一些点拓扑指数的概念:
以下是几个引理:
引理1 设x,y∈Z+,则-,等号成立的充要条件是x=y.
证明 我们很容易得到

等号成立的充要条件是x=y.
等号成立的充要条件是a=b.
2 主要结果
定理1 设G是一个n(n≥3)阶连通图,且最小度δ≥2,
左边等号成立的充要条件是G≌Cn,右边等号成立的充要条件是G≌C3.
左边等号成立的充要条件是G≌C4,右边等号成立的充要条件是G≌K4.证明 由vi和vj的对称性,不妨设2≤dj≤dj≤n-1,我们考虑函数

知F(x,y)是关于y的单调递增函数.由于2≤x≤y≤n-1,则F(x,y)的最小值是F(x,x).又F(x,x)=是关于x的单调递增函数,于是F(x,x)在(x,x)=(2,2)处能够得到最小值,即F(x,x)≥F(2,2)=2.因此ABC(G)≥X(G),等号成立当且仅当x=y=2即G≌Cn.
由于F(x,y)是关于y的单调递增函数.另一方面,我们也能够得到F(x,y)的最大值是F(x,n-1).
那么F(x,n-1)关于x的单调递减函数,因此F(x,n-1)≤F(2,n-1)=,等号成立当且仅
当x=2.
当x=n-2,则
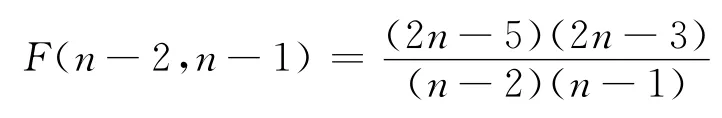
由此,我们得到F(x,n-1)的最大值是max{F(2,n-1),F(n-2,n-1),F(n-1,n-1)}.当n≥5或n=3时,利用作差法我们很容易得到
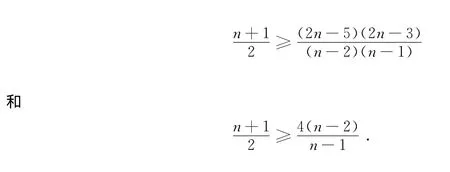

等号成立的充要条件是G≌C3.
等号成立的充要条件是G≌K4.
定理2 设G是一个n≥2阶的连通图,则

等号成立的充要条件是G≌K2.

第一个不等式等号成立当且仅当du=dv,第二个不等式等号成立当且仅当du=dv=1.
等号成立的充要条件是G≌K2.
定理3 设G是一个n≥2阶的连通图,其最大度为Δ,则
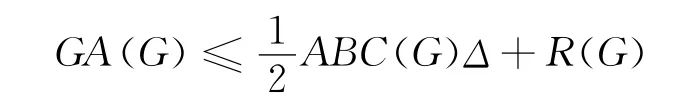
等号成立的充要条件是G≌K2.

第一个不等式等号成立当且仅当du=dv,第二个不等式等号成立的等价条件是du=dv=1.
等号成立的充要条件是G≌K2.
[1]Estrada E,Torres L,Rodriguez L,et al.An atom-bond connectivityindex:modelling the enthalpy of formation of alkanes[J].Indian J Chem,1998,37A:849~855.
[2]Furtula B,Graovac A,Vukicevic D.Atom-bond connectivity index of trees[J].Discrete Appl Math,2009,157:2828~2835.
[3]Das K C.Atom-bond connectivity index of graphs[J].Discrete Appl Math,2010,158:1181~1188.
[4]Gan L,Hou H,Liu B.Some Results on Atom-Bond connectivity Index of Graphs[J].MATCH Commun Math Comput Chem,2011,66:669~680.
[5]Zhong L,Cui Q.On a relation between the atom-bond connectivity and the first geometric-arithmetic indices[J].Discrete Appl Math,2015,185:249~253.
[6]Zhong L,Xu K.Inequalities between vertex-degree-based topological Indices[J].MATCH Commun Math Comput Chem,2014,71:627~642.
[7]Ali A,Bhatti A,Raza Z.Further inequalities between vertex-degree-based topological indices[J].Interation Journal of Applied &computatio Mathematics,2014,doi:10.1007/S408 19-016-0213-4.
Relations on ABCindex and several vertex-degree-based topological indices
(College of Mathematics and statistics,Hubei Normal University,Huangshi 435002,China)
In order to take factors into account but at the same time to keep the spirit of Randic index,Estrada et al.proposed the atom-bond connectivity(ABC)index.The ABC index provides a good model for the stability of linear and branched alkanes as well as the strain energy of cycloalkanes.In this paper,we established some relations between ABC index and several other vertex-degree-based topological indices.
Atom-bond connectivity index;vertex-degree-based topological indices;X index
GAN Lu
O157.6
:A
1009-2714(2016)04-0014-04
10.3969/j.issn.1009-2714.2016.04.004
2016—05—02
国家自然科学基金(NSFC):11601139.
甘露(1985— ),女,湖北黄石人,硕士,研究方向为图论.
