基于分布鲁棒优化的光伏电站并网极限容量研究
2016-02-16向加佳刘建华朱雪松高山
向加佳,刘建华,朱雪松,高山
(1.长沙理工大学电气与信息工程学院,长沙市 410114;2.国网湖南省电力公司技术技能培训中心,长沙市 410131;3.国网湖南省电力公司桃江县供电分公司,湖南省桃江县 413400)
基于分布鲁棒优化的光伏电站并网极限容量研究
向加佳1,刘建华1,朱雪松2,高山3
(1.长沙理工大学电气与信息工程学院,长沙市 410114;2.国网湖南省电力公司技术技能培训中心,长沙市 410131;3.国网湖南省电力公司桃江县供电分公司,湖南省桃江县 413400)
针对光伏电站出力的不确定性,以及描述出力的概率分布函数难以准确获取的特点,提出将分布鲁棒线性优化理论用于研究光伏电站并网后的极限容量问题,建立了基于系统运行约束条件下的光伏电站极限容量的分布鲁棒优化模型,模型中的随机变量为太阳辐射强度,结合其上下限与期望来描述光伏电站出力的不确定,并通过对偶理论将模型转化为确定性的线性规划问题,以便于求解。在某修正的Garver’s 6节点系统中,对模型进行验证,结果表明:不同的并网位置、太阳辐射变化范围均明显影响了光伏电站并网后的极限容量,并且与盒式鲁棒优化方法相比,分布鲁棒优化方法能得到更优的结果,同时该模型还能给出在最优性与鲁棒性之间灵活转换的计算结果,进而验证了该模型与方法的可行性和有效性。
分布鲁棒线性优化;光伏电站;极限容量;不确定性
0 引 言
随着大规模光伏电站并网,光伏电站出力的不确定性会对系统的稳定性造成一定的冲击,因此,综合考虑光伏电站输出功率波动及电网约束的极限容量研究,成为系统规划运行的重要内容,也为大型并网光伏电站的建设提供了参考依据。
电力系统中针对不确定性问题的建模方法主要有随机规划方法和鲁棒优化方法。对于随机规划方法,通过随机变量表示不确定因素,需要事先得到随机变量的概率分布,常用的有机会约束方法和条件风险方法。文献[1]中建立了机会约束规划下的光伏电站并网极限容量模型,由于其在数学上具有非凸性,将难以获得全局最优解,且求解过程比较复杂。文献[2]引入条件风险方法构建了计及极端情况的光伏发电极限容量优化模型,虽然其具有数学凸性,能够求得全局最优解,但采用蒙特卡罗抽样时会产生较多的离散样本,增大了计算量。相比随机规划方法,鲁棒优化无需知道不确定参数的概率分布情况,只需要获得不确定参数的区间范围即可。文献[3]采用盒式不确定集描述风速的变化,求解风电场的最大装机容量,然而该方法在考虑多个节点并网时的计算过于复杂,且对经济性的敏感度不高,也无法充分利用已得到的概率统计信息,导致所求得的解过于保守。
光伏电站出力的概率分布函数一般根据已有实测数据的分析和统计来获取,但其期望、方差以及协方差均存在不确定性,所以概率分布函数也是不确定的。基于光伏发电出力属于一定的区间范围,但概率分布又存在一定的不确定性,提出运用鲁棒优化和随机规划相结合的分布鲁棒优化方法来解决并网光伏电站极限容量的计算问题,该方法结合随机变量的期望与区间来表示光伏发电出力的不确定性,相比盒式鲁棒优化方法,虽然只多了期望值,但所考虑到的安全信息会多于盒式鲁棒,具有更强的通用性[4-5]。
本文运用分布鲁棒优化理论建立计及出力不确定性的光伏电站并网极限容量的优化模型,依据对偶理论将其转换为确定性的规划问题进行求解,通过改变不确定参数的变化幅度,可使结果在最优性与鲁棒性之间灵活转换。
1 分布鲁棒线性优化理论
由于常规鲁棒优化对经济性的敏感度不高,Seng-Cheol Kang在已有鲁棒线性优化研究基础上,提出了分布鲁棒线性规划模型,更符合工程实际且其计算求解过程更加简单[6-7]。
常规线性规划数学模型为
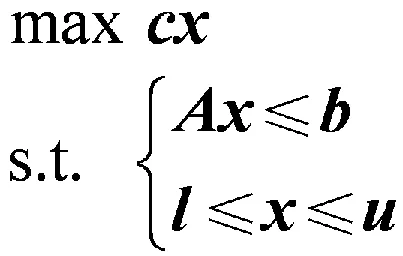
(1)
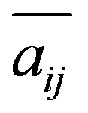
将变化约束变量Γi(i=1,…,m)引入每个不等式约束中,Γi是实数且有Γi≤Ji。该模型的关键在于借对A中每行不确定参数变化幅度的控制,使优化结果得到可靠性与经济性的平衡。记,,定义集合:
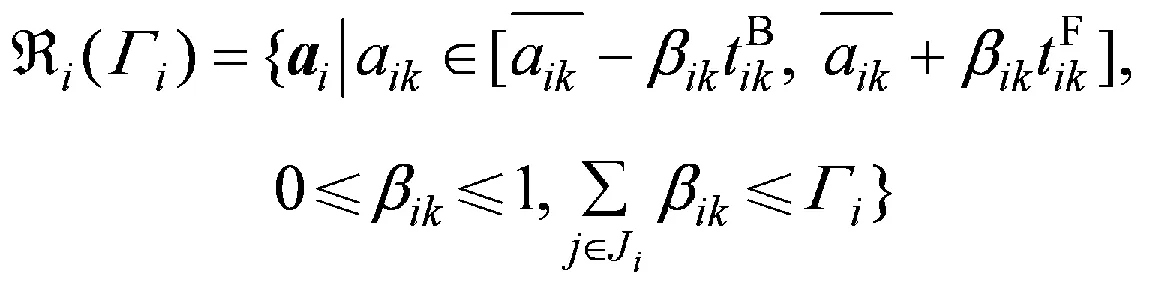
(2)
式中:ai表示第i行的不确定参数的向量。考虑不确定参数的常规线性规划模型(1)的分布鲁棒模型为

(3)
相应的鲁棒对等模型为
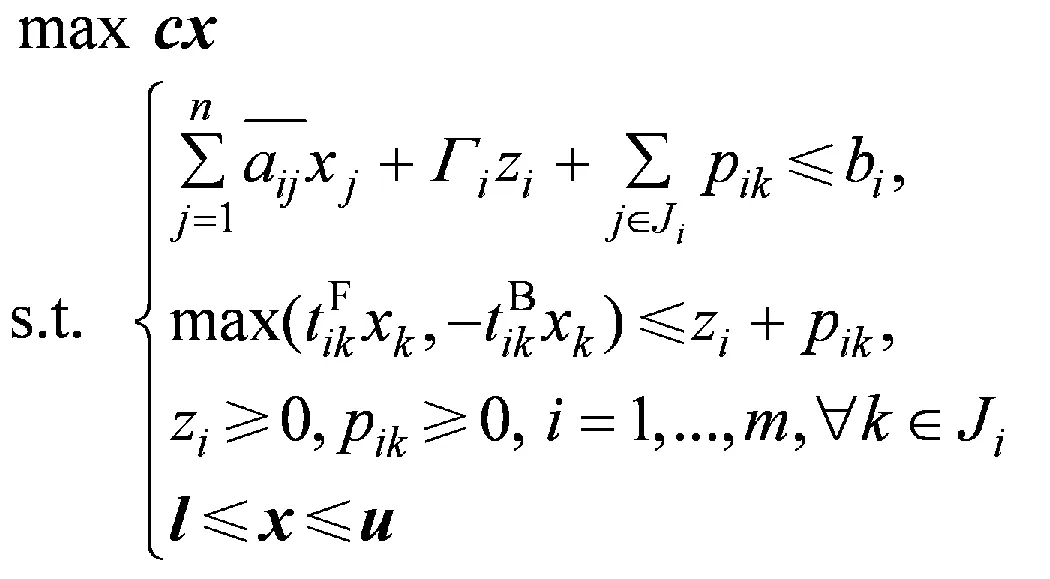
(4)
其中模型(3)转化为模型(4)时新引进了zi与pik这2个决策变量。由模型(4)可知,计及不确定参数的常规线性规划模型(1)已变为一个确定性的线性规划问题,用一般线性规划方法进行求解即可。
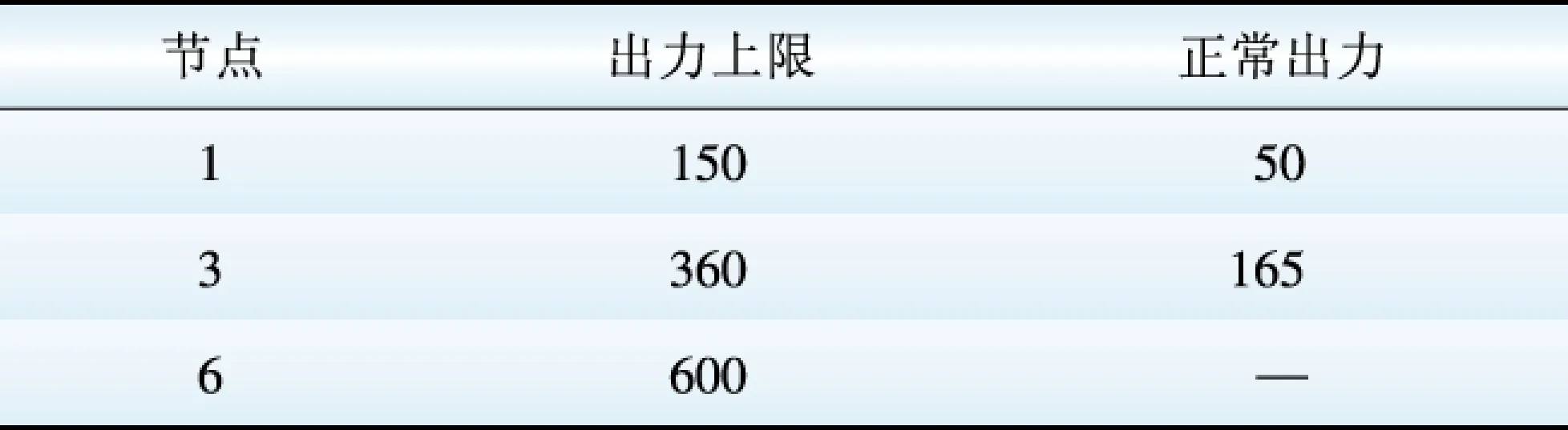
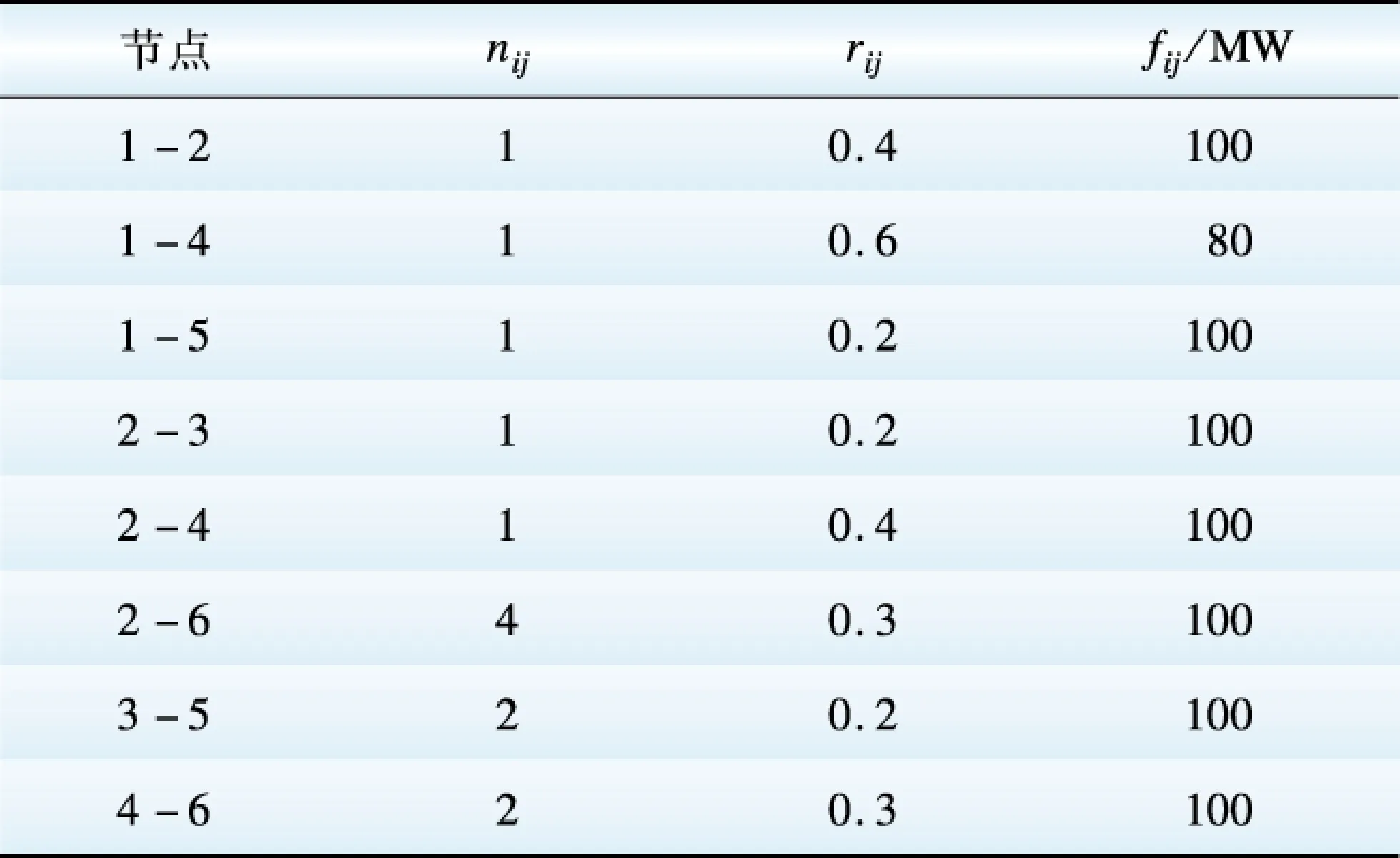
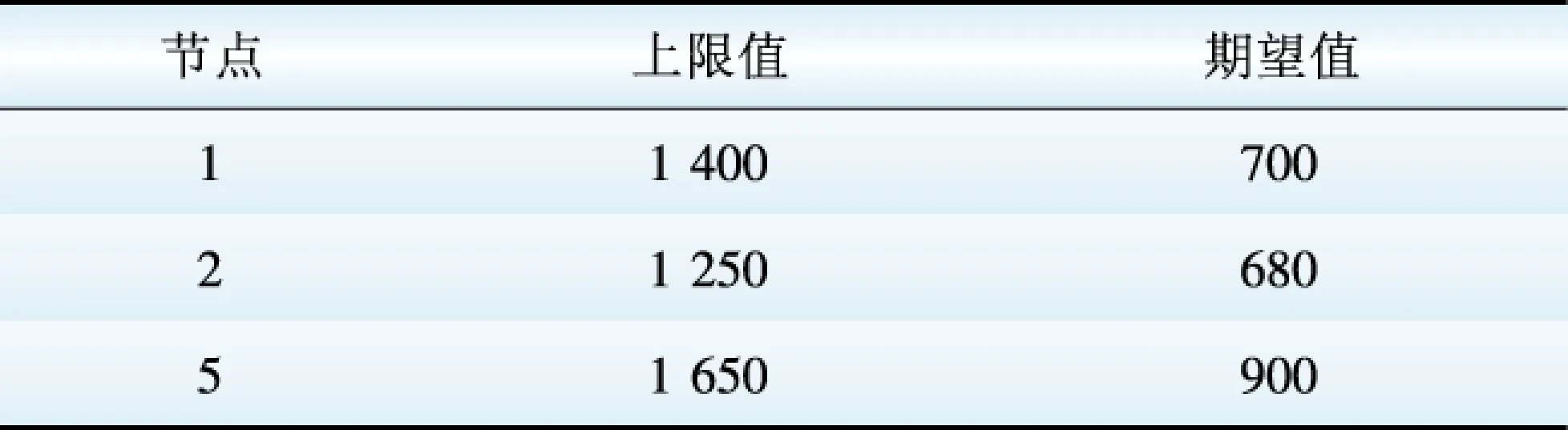
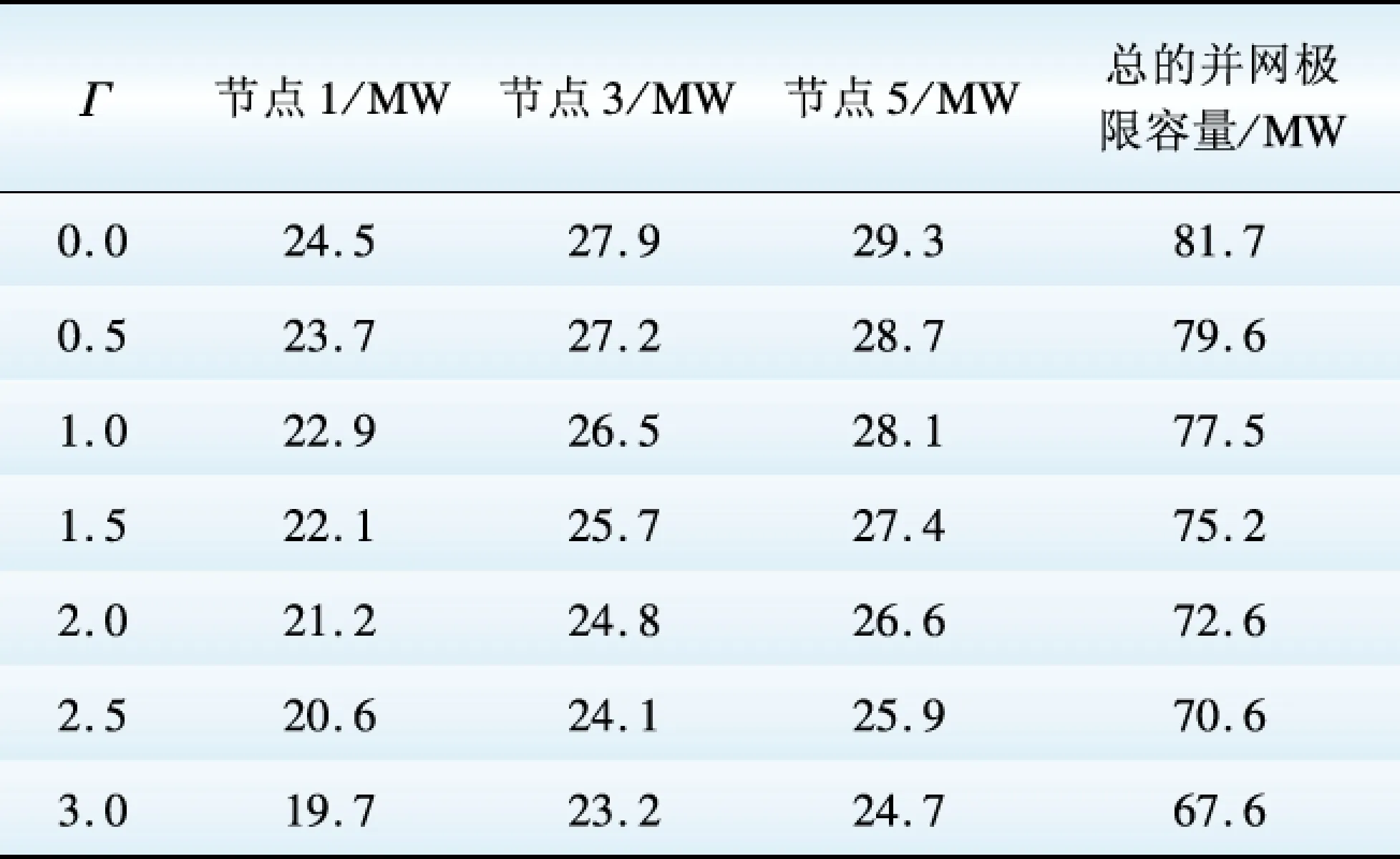
对Γi进行分析可知,Γi 当Γi 2.1 极限容量的一般模型 光伏电站的输出功率Ppv主要与太阳辐射强度有关,两者之间存在近似线性关系,其表达式为 (6) 式中:μn为逆变器的效率系数;Is为太阳实际辐射强度;In为标准条件下的太阳辐射强度,通常为1.0 kW/m2;Cpv为光伏电站并网的容量[8]。 并网光伏电站极限容量的一般数学模型可表示为 (7) 2.2 极限容量的分布鲁棒优化模型 系统有n+1个节点(从0,…,n)、m条支路(从1,…,m),假定平衡节点为节点0,将其看作有功出力为Pg0的电源节点。节点i处接入的光伏电站所在区域的太阳辐射强度的期望值E(Isi)=Isi,Isimax和Isimin分别为节点i处接入的光伏电站所在区域的太阳辐射强度的上下限。H是m×n阶矩阵,表示依据特定网络结构及系统线路参数求解出的支路注入功率与节点注入功率的关联矩阵。则所需求解的并网光伏电站极限容量的分布鲁棒优化模型为 (8) 假设平衡节点以外的常规机组出力方式确定,结合模型(8)和式(6)中可得如下不等式约束(i=1,…,m): (9) (10) (11) (12) 上述不等式约束中不确定参数均为Isj(j=1,…,n),所以每个不等式约束的变化约束变量Γ相同。假设Jpv表示实际接入光伏电站的节点集合,Jpv表示集合Jpv中元素的个数,有Γ≤Jpv。 以式(12)为例,其分布鲁棒优化模型的鲁棒对等模型为 (13) 式(9)—(11)同样也可转化为相应分布鲁棒优化模型的鲁棒对等模型。式(13)中,zi和pik不具有任何物理意义,为鲁棒对等模型中新引入的决策变量,且每个对等模型中zi与pik的取值并不相同。对于每个不等式约束,其鲁棒对等模型中都增加1+Jpv个决策变量,Jpv个线性不等式。实际中,等效的光伏电站节点数并不多,即Jpv不大。模型(8)的鲁棒对等模型为确定性的线性规划模型,可用一般线性规划方法进行求解。 (14) 3.1 算例参数 在某修正的Garver’s 6节点系统中对光伏电站并网极限容量的分布鲁棒优化模型进行验证,其中发电机参数、负荷参数、系统支路参数如表1—3[7]所示。表3中nij表示支路i和j之间的线路数,rij表示支路i和j之间一条线路的电抗值,fij表示支路i和j之间单条线路的越限功率。 表1 发电机参数 Table 1 Parameters of generators MW 表2 负荷参数Table 2 Parameters of loads MW 表3 系统支路参数Table 3 Parameters of system branch 该算例的分布鲁棒优化模型的不等式约束有18个,包括8个式(12)类型的不等式约束,分别记作式(12-1)—(12-8),用P12-1—P12-8表示其被违反的概率上限,可通过式(14)来求解。同理,另外10个不等式约束用(9-1)、(10-1)、(11-1)—(11-8)表示,相应的概率上限用P9-1、P10-1、P11-1—P11-8表示。假设接入节点6的常规机组为平衡机,逆变器的效率系数μn取0.95,标准条件下的太阳辐射强度In取1 000 W/m2,接入系统不同节点处的光伏电站所在区域的太阳辐射强度相关参数如表4—5[9-12]所示。Γ是通过控制太阳辐射的变化范围从而衡量光伏电站出力变化范围的参数,其取值可以是0到Jpv之间的任意实数。 表4 太阳辐射强度参数1 Table 4 Parameters 1 of solar radiation intensity W/m2 表5 太阳辐射强度参数2Table 5 Parameters 2 of solar radiation intensity W/m2 3.2 仿真结果分析 设计如下3个仿真方案。 方案Ⅰ:光伏电站接入系统的节点1,将分布鲁棒优化模型的结果与盒式鲁棒优化模型的结果进行比较,Γ的取值不同时,极限容量和相应不等式约束被违反的概率上限的计算结果见表6。 表6 方案Ⅰ的计算结果 Table 6 Calculation results of case 1 由表6可以看出,在并网光伏电站极限容量的计算上,分布鲁棒优化模型比盒式鲁棒优化模型能得到更好的结果。这是因为盒式鲁棒优化方法在刻画不确定参数时要求其扰动参数的取值为对称区间,所以在该算例中盒式鲁棒优化方法只能计算对太阳辐射强度考虑最全面时的并网极限容量,也就是说只有Γ取1.0时才有相应的计算结果。而分布鲁棒优化模型通过改变Γ的取值,能得到经济性更好的结果,但是相应的可靠性将降低。通过不等式约束被违反的概率上限来衡量分布鲁棒优化模型所求结果的可靠性,由于在本算例的分布鲁棒优化模型中,只有式(12-7)的不等式约束存在可能违反的情况,所以由P12-7来衡量结果的可靠性,P12-7表示支路3-5的功率越限概率上限,当Γ的取值变小时,结果的经济性变好,但相应的功率越限概率将变大,可靠性会变差。 方案Ⅱ:在节点1、2、5处同时接入光伏电站,各节点所接光伏电站的太阳辐射强度参数见表4,Γ的取值不同时,并网极限容量的计算结果见表7。 表7 方案Ⅱ的计算结果 Table 7 Calculation results of case 2 方案Ⅲ:在节点1、3、5处同时接入光伏电站,各节点所接光伏电站的太阳辐射强度参数见表5,Γ的取值不同时,并网极限容量的计算结果见表8。 表8 方案Ⅲ的计算结果 Table 8 Calculation results of case 3 对比表7、8可知,不同的并网节点,其并网极限容量有明显的不同,这对于电网规划时如何选取光伏电站接入地点提供了可靠的参考意见。并且通过调整Γ的大小可以使结果在最优性与鲁棒性之间灵活转换。随着Γ的取值增大,考虑的太阳辐射强度的变化范围会扩大,从而对光伏电站的出力变化情况考虑更全面,则光伏电站的并网容量因受到限制而变小(可靠性递增,经济性递减),反之,Γ的取值越小,并网容量会越大(可靠性递减,经济性递增)。这也说明系统的经济性与可靠性是一对矛盾体,想要结果更优就会面临更大的风险。 (1)针对并网光伏电站出力随机且其概率分布难以准确预测的问题,提出采用分布鲁棒优化理论建立了系统运行约束条件下的光伏电站并网极限容量的分布鲁棒优化模型。模型中通过太阳辐射强度的平均值和上下限来描述光伏发电出力的不确定性,更切合工程实际。运用对偶理论使模型转换为确定性的规划问题,便于求解。 (2)约束变量Γ的不同取值下,侧重于可靠性或经济性的计算结果不同。 (3)分布鲁棒优化模型所得结果会优于盒式鲁棒优化模型,避免了盒式鲁棒求解结果偏于保守的不足;且分布鲁棒优化方法可用于多节点接入光伏电站的情况,解决了盒式鲁棒优化方法在多节点接入时计算过于复杂的难题。 [1] 王一波, 许洪华. 基于机会约束规划的并网光伏电站极限容量研究[J]. 中国电机工程学报, 2010, 30 (22): 22-27. WANG Yibo, XU Honghua. Research of capacity limit of grid-connected photovoltaic power station on the basis of chance-constrained programming[J]. Proceeding of the CSEE, 2010, 30 (22): 22-27. [2] 周任军, 黄灵资, 王靓, 等. 基于风险和条件 风险方法的光伏电站并网极限容量[J]. 电力自动化设备, 2012, 32(6): 1-5. ZHOU Renjun, HUANG Lingzi, WANG Liang, et al. Capacity limit calculation based on risk and conditional risk method for grid-connected photovoltaic power station[J]. Electric Power Automation Equipment, 2012, 32(6): 1-5. [3] 李斯, 周任军, 童小娇, 等. 基于盒式集合鲁棒优化的风电并网最大装机容量[J]. 电网技术, 2011, 35(12): 208-213. LI Si, ZHOU Renjun, TONG Xiaojiao, et al. Robust optimization with box set for maximum installed capacity of wind farm connected to grid[J]. Power System Technology, 2011, 35(12): 208-213. [4] 周任军, 闵雄帮, 童小娇, 等. 电力环保经济 调度矩不确定分布鲁棒优化方法[J]. 中国电 机工程学报, 2015, 35 (13): 3248-3256. ZHOU Renjun, MIN Xiongbang, TONG Xiaojiao, et al. Distributional robust optimization under moment uncertainty of environmental and economic dispatch for power system[J]. Proceeding of the CSEE, 2015, 35 (13): 3248-3256. [5] 朱雪松, 汪静, 刘志勇. 采用分布鲁棒优化方法的最小切负荷量计算[J]. 国外电子测量技术, 2015, 34(10): 37-44. ZHU Xuesong, WANG Jing, LIU Zhiyong. Calculation for minimum load-curtailment using distributional robust optimization[J]. Foreign electronic measurement technology, 2015, 34(10): 37-44. [6] KANG S C. Robust linear optimization using distributional information[D]. Boston: Boston University, 2008. [7] 陈雁, 文劲宇, 程时杰. 电网规划中考虑风电场影响的最小切负荷量研究[J]. 中国电机工程学报, 2011, 31(34): 20-27. CHEN Yan, WEN Jinyu, CHENG Shijie. Minimum load-curtailment in transmission network planning considering integrated wind farms[J]. Proceeding of the CSEE, 2011, 31(34): 20-27. [8] 王福菊, 毛文达, 杨慢慢. 基于可信性理论并网光伏发电系统极限容量模型研究[J]. 华东电力, 2014, 42(9): 1868-1872. WANG Fuju, MAO Wenda, YANG Manman. Ultimate capacity model of grid-connected PV power generation system based on the credibility theory[J]. East China Electric Power, 2014, 42(9): 1868-1872. [9] 李春来, 王晶, 杨立滨. 典型并网光伏电站的等值建模研究及应用[J]. 电力建设, 2015, 36(8): 114-120. LI Chunlai, WANG Jing, YANG Libin. Equivalent modeling research and application of typical grid connected photovoltaic power station[J].Electric Power Construction,2015, 36(8): 114-120. [10] 程泽, 韩丽洁, 李思宇, 等. 光伏发电功率 的智能预测算法[J]. 电力建设, 2014, 35(7): 34-38. CHENG Ze, HAN Lijie, LI Siyu, et al.Intelligent forecasting algorithm for photovoltaic power station[J].Electric Power Construction,2014, 35(7): 34-38. [11] 赵书强, 谢宇琪, 刘大正, 等. 基于模糊随机理论的短期太阳辐射强度预测[J]. 电力自动化设备, 2015, 35(7): 101-105. ZHAO Shuqiang, XIE Yuqi, LIU Dazheng, etal.Short-term solar radiation intensity forecasting based on fuzzy-random theory[J]. Electric Power Automation Equipment, 2015, 35(7): 101-105. [12] 单增罗布, 朱振岭, 次仁尼玛, 等. 西藏羊八井辐射观测初步分析[J]. 大气科学学报, 2012, 35( 4) :495-501. DANZENGLUOBU, ZHU Zhenling, CIRENNIMA, et al. Preliminary analyses on radiation in Yangbajing of Tibet[J]. Transactions of Atmospheric Sciences, 2012, 35(4): 495-501. (编辑 蒋毅恒) Research on Capacity Limit of Grid-Connected Photovoltaic Power Station Based on Distributional Robust Optimization XIANG Jiajia1, LIU Jianhua1, ZHU Xuesong2, GAO Shan3 (1.College of Electrical and Information Engineering, Changsha University of Science and Technology, Changsha 410114,China;2. Technical Training Center of State Grid Hunan Electric Power Company, Changsha 410131, China;3.Taojiang Power Supply Subsidiary of State Grid Hunan Electric Power Company,Taojiang 413400,Hunan Province, China) In allusion to the uncertainty of photovoltaic power station output and the difficulty to accurately describe the probability distribution function of output, this paper adopts distributional robust linear optimization method to study the capacity limit of grid-connected photovoltaic power station. We establish the distributional robust linear optimization model for the capacity limit of photovoltaic power station based on the constraint conditions of system operation. The solar radiation intensity is taken as random variable in the model, whose bound and expectation are used to describe the uncertainty of photovoltaic power station output. The model is transformed to certain linear programming problems via duality theory, which is easy to be solved. We verify the model in a modified Garver’s 6-bus system. The results show that the capacity limit of grid-connected photovoltaic power station varies under the effect of factors such as the grid-connected access position, and solar traditional variation range. The optimization result obtained by distributional robust optimization method is better than that obtained by cassette robust optimization, and the proposed model can provide flexible calculation results between optimization and robustness, thereby the practicality and effectiveness of the model are proved. distributional robust linear optimization; photovoltaic power station; capacity limit; uncertainty TM 744 A 1000-7229(2016)06-0151-06 10.3969/j.issn.1000-7229.2016.06.021 2016-03-17 向加佳(1990),女,通讯作者,硕士研究生,研究方向为电力系统运行与控制; 刘建华(1964),男,硕士,副教授,硕士生导师,研究方向为电力系统运行与控制; 朱雪松(1989),女,硕士,研究方向为电力系统配网优化、规划与运行。 高山(1989),男,硕士,研究方向为微电网的优化调度。
2 并网光伏电站极限容量的分布鲁棒优化模型
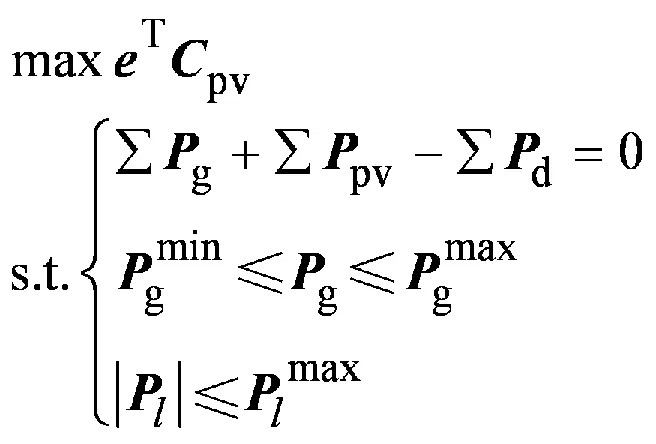

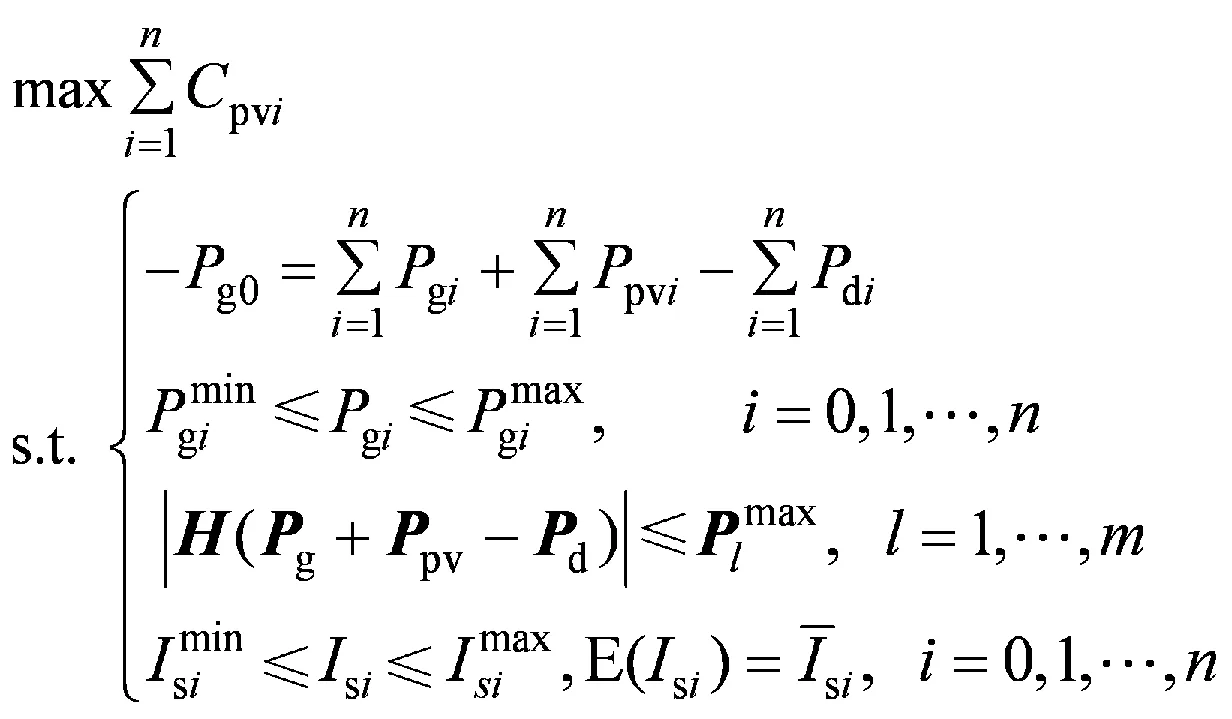

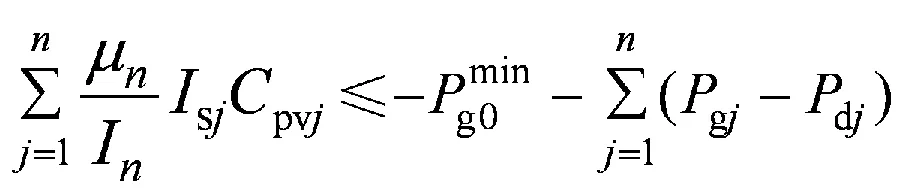
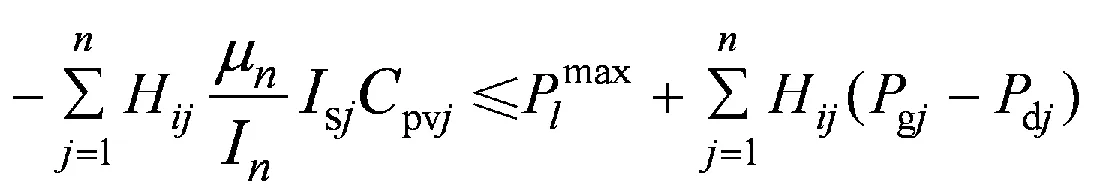

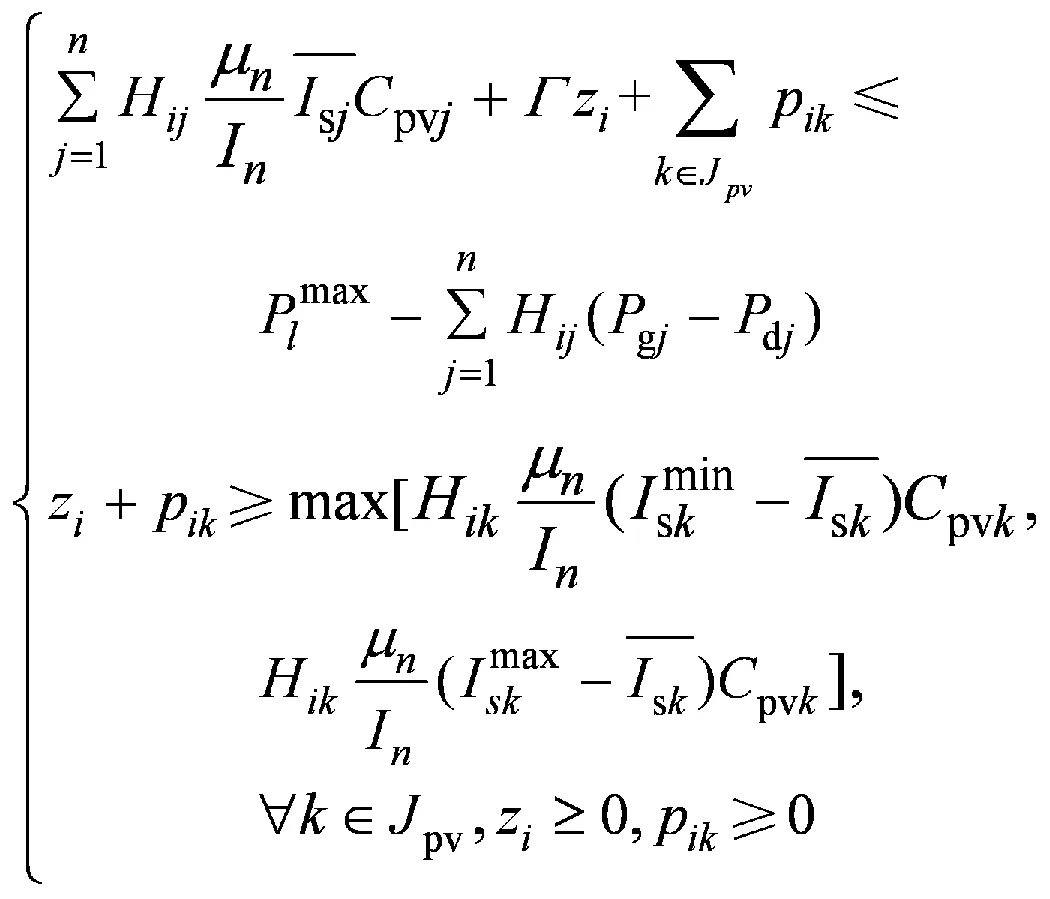

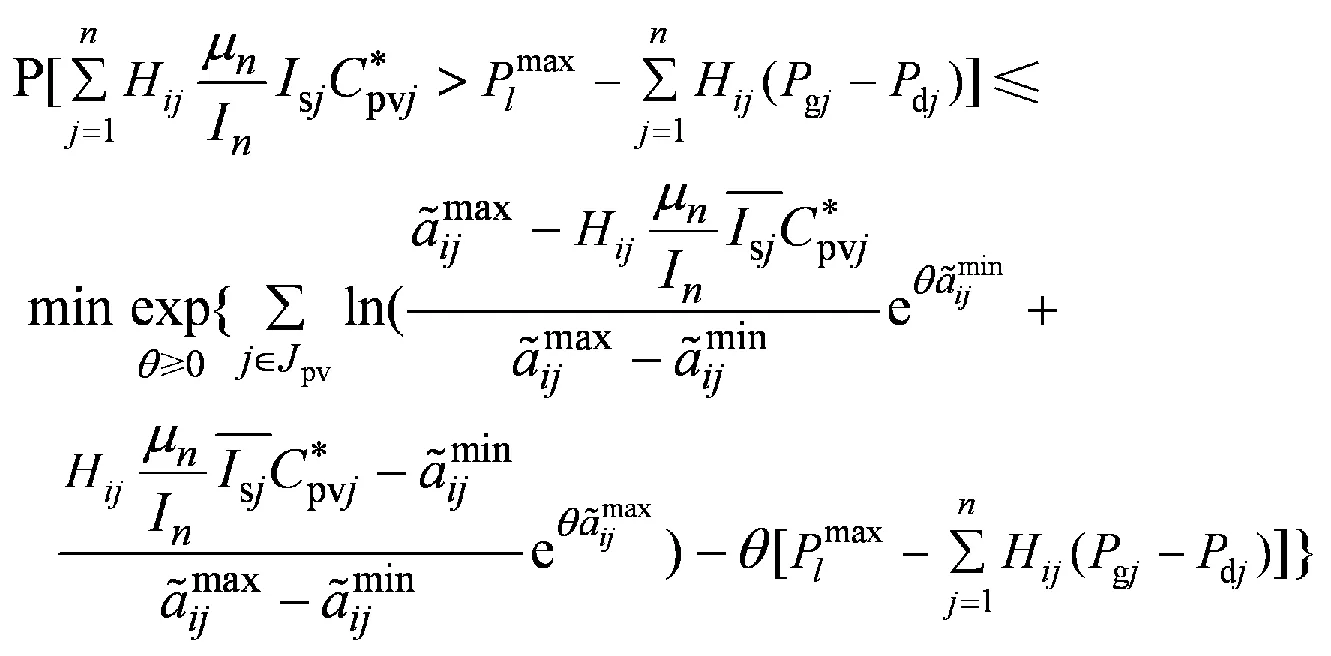
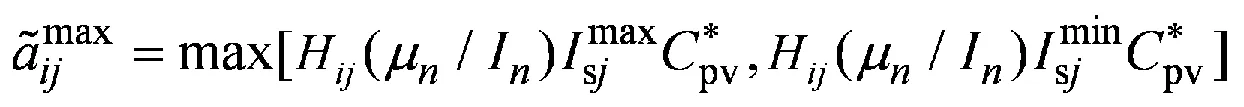
3 算例分析




4 结 论
