减少弃风损失的储能容量和布局优化研究

吴俊玲，张彦涛，秦晓辉，梁才浩

(中国电力科学研究院，北京市 100192)

减少弃风损失的储能容量和布局优化研究

吴俊玲，张彦涛，秦晓辉，梁才浩

(中国电力科学研究院，北京市 100192)

针对我国大规模风电接入地区因系统调峰能力不足引起的大量弃风问题，提出采用大容量储能电池提高系统调峰能力、减少弃风损失的储能充放电策略。基于所提出的储能恒功率充放电策略，建立储能电站容量和布点优化的数学模型，并采用遗传算法进行求解。该模型以储能电站的投资和运行成本、网络损耗、调峰不足弃风及风电送出通道阻塞弃风损失之和最小为优化目标，考虑了储能电站的峰谷电价收益、计及了风力发电的碳减排效益，并满足电网的安全运行约束。最后，利用IEEE RTS79系统进行储能布局优化分析，验证了方法的有效性。应用该方法能够为解决大规模风电并网地区的弃风问题提供技术解决方案。

弃风；电池储能；优化；遗传算法

0 引 言

风电出力具有波动性和不确定性，往往与负荷曲线不一致。我国风电集中的地区风电出现反调峰的概率较大[1]。

我国以煤为主的能源资源特点决定了以煤电为主的电源结构，而在煤电装机中供热机组又占有较大比重，冬季供热机组基本没有调峰能力，因此，在夜间低谷负荷时段系统接纳风电的能力往往受到常规发电机组最低技术出力的限制。尤其在燃煤火电和供热机组装机比例较高的地区，调峰不足成为制约风电消纳能力的主要因素。在我国东北、西北等大型风电基地，已经暴露出了由于系统调峰能力不足而引起大量弃风的问题[2]。另外，在风电基地开发初期，风电场汇集站的变电容量和风电基地送出通道的输电能力不足，也是造成风电大发时段弃风的重要因素[3]。

电池储能的能量密度高，响应迅速，具有双向的功率吞吐能力，因此大容量电池储能装置的应用是提高系统调峰能力的有效手段。随着储能技术的飞速发展，除传统的抽水蓄能电站外，国内外已有多个大容量电池储能电站参与系统调峰的示范应用工程[4-5]。与抽水蓄能电站相比，电池储能电站的建设地点和运行方式更为灵活，通过在负荷低谷时段和风电送出通道输电能力不足时段吸收多余风电，在高峰负荷时段和风电出力较小时段放电，能够有效地减少弃风损失。

现阶段储能系统的高成本仍然是限制其大规模应用的关键因素，为了衡量储能减少弃风损失的经济性，有必要研究储能的容量配置问题，进而评估储能运营的经济性。在储能优化配置方面，国内外已有大量学者进行了相关的研究工作[6-12]。文[6]针对储能技术在电网侧、用户侧和新能源发电3个不同的主要应用场合，对其应用规划和效益评估方法进行研究和归纳。文[7]从储能应对风电短时间尺度功率波动的角度分析了储能的作用并研究了储能容量优化的方法。文[8-11]从跟踪负荷和风电长时间尺度调功率变化的角度分析了储能在“削峰填谷”方面的作用并进行容量的优化，但未对储能电站的优化布局进行研究。文[12]从配电网参与功率调节的角度对含风电、光伏的配电系统的分布式储能进行了优化配置。

本文针对我国大规模风电接入地区因系统调峰能力不足引起的大量弃风问题，研究电池储能容量和布点的优化。首先提出3种实用的提高系统调峰能力减少弃风损失的储能充放电策略，定性比较不同充放电策略对于减少弃风的效果。然后，基于储能的恒功率充放电策略提出储能电站容量和布点的优化方法，并采用遗传算法对该优化问题进行求解。最后，利用IEEE RTS79系统对所提优化模型和求解方法进行验证。

1 减少弃风损失的储能充放电策略

电池储能系统的双向电力电子变流器可以在容量和功率限值内按照指令控制储能的充放电[13]。为充分发挥储能的容量效益并方便对储能进行控制，需要确定合理的储能充放电策略，即每个时刻电池是否充放电，以及充放电功率的大小[14]。

为缓解系统调峰不足而引起的弃风问题，提出了3种实用的储能充电策略，示意图如图1所示。图中横坐标为时间，纵坐标Pps为系统的调峰需求，Pps可由下式求取

Pps=Ps,min-(PLoad-PWind)

(1)

式中PLoad为系统负荷；PWind为风电出力；Ps,min为系统常规发电机组的最低技术出力。Pps>0表示调峰能

力不足，需要储能充电来减少弃风电量。

图1中粗实线表示储能各时刻的充电功率，Ps为额定充电功率，充电功率曲线与横坐标所围面积即为储能的额定存储电量Ws，阴影部分的面积即为储能充电后减少的弃风电量。

1.1 跟踪调峰需求的充电策略

根据预测得到的次日系统调峰需求曲线Pps确定每一时刻储能的充电功率。如图1(a)所示，从t1时刻开始，Pps>0，储能开始充电。当调峰需求Pps小于储能的最大充电功率Ps时，储能充电功率变化曲线与调峰需求曲线一致；当调峰需求大于储能最大充电功率时，储能以额定充电功率Ps充电，直到t2时刻储能电量充满至Ws。

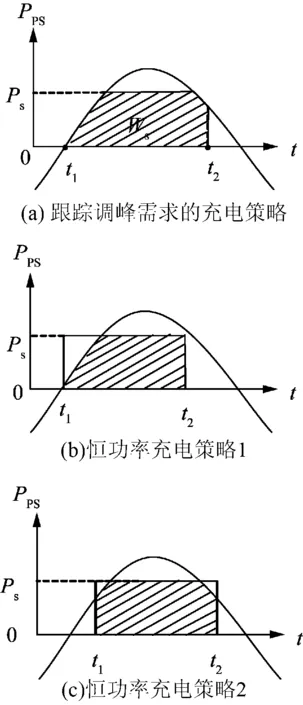
图1 电池储能充电策略示意图Fig.1 Battery energy storage and charging strategy

1.2 恒功率充电策略1

该策略从Pps>0的起始点t1开始，储能以额定充电功率Ps进行充电，直到t2时刻储能电量充满。图1(b)所示，储能的充电时长为额定功率充电时间Ts=t2-t1=Ws/Ps。

1.3 恒功率充电策略2

该策略储能仍以额定充电功率Ps进行充电，充电时长亦为额定功率充电时间。但充电的起止时刻不同，其确定方法为：用一条水平线从Pps的最大值开始向下移动，直到水平线与Pps相交得到的时间(t2-t1)恰好等于储能的额定功率充电时间Ts。

同理，可以利用预测得到的次日发电功率不足曲线确定储能的放电策略。如果存在发电功率不足，则可以依照上述方法确定3种不同的储能充电策略。若不存在发电功率不足，则可以利用上述策略1.3的方法在净负荷曲线的高峰时段确定储能放电的起始和结束时间。

1.4 3种充电策略的定性比较

采用跟踪调峰需求的充电策略，储能的功率和容量能够得到最充分的发挥，储能设备在额定充放电功率和存储容量相同的情况下，减小弃风的效果最好。但采用该策略，需要在每一时刻重新确定储能的充电功率，给储能系统的运行控制增加了难度。

采用恒功率充电策略1，能够较容易地确定充电的起始和终止时刻，便于储能的运行控制，但储能的容量不能得到充分发挥，减少弃风的效果不佳。

采用恒功率充电策略2，储能的运行控制也较为简单。从图1的示意图可以看出，其减少弃风电量的效果较恒功率充电策略1更好。

2 储能容量和布点优化模型

从系统层面利用储能装置提高调峰能力，减少弃风损失，关注的是储能在整个电力平衡中发挥的作用。定性来说，在储能类型和容量相同的条件下，集中布放要比分散布放更节省投资。但储能布放位置和容量不同，会对网络损耗产生一定的影响。另外，当系统存在网络阻塞引起的弃风问题时，储能的布放位置对弃风的影响就更为显著。

2.1 目标函数

优化的目标为储能的投资和运行成本、网络损耗以及弃风损失之和：

minC=fcrCinv.s+Cope.s+Closs.net+ Closs.w-Cprice,s

(2)

式中：Cinv,s为储能的投资成本；fcrCinv,s表示储能的投资年值；Cope,s为储能的运行成本，主要包括储能的运行维护费用和充放电损耗；Closs,net为网络损耗；Closs,w为弃风损失，包括因系统调峰能力不足和风电送出通道阻塞引起的弃风损失；Cprice,s是储能充电和放电时段的电价之差带来的收益，因此储能放电时电价为正，充电时电价为负。

2.1.1 储能电站投资和运行成本

包括固定成本Cfix,s和可变成本Cvar,s两部分

Cinv,s=Cfix,s+Cvar,s

(3)

式中固定成本是指与储能规模基本无关部分的投资费用，主要包括储能电站的通信和控制等辅助设施的投资费用。可变成本是指与储能功率或容量直接相关的部分成本，由功率成本和容量成本构成，主要包括变流器和电池本体的投资费用。

为了简化起见，研究中可变成本只考虑与储能功率或容量呈线性关系的部分，表示为

Cvar.s=Cp.sPs+Cw.sWs

(4)

式中Cp,s为储能系统的单位功率成本，包括变流器和液流电池电极的单位功率成本；Cw,s为储能系统单位容量成本，主要包括液流电池电解液或锂电池的单位容量成本。

储能系统使用寿命为

(5)

式中：Tlife为对应充放电深度下储能系统的循环寿命；Lcyc_year为年充放电循环次数，在恒功率充放电策略下，也就是储能1年中投入运行的次数。

不考虑储能系统正常使用期内的设备更换成本，根据储能系统的使用寿命和基准收益率，将储能系统的总投资成本在寿命期内进行成本分摊，得到储能系统的投资年值：

(6)

储能运行费用主要包括年运行维护成本COM,s和充放电量损耗CLoss,s，即

Cope.s=COM.s+CLoss.s

(7)

正常的储能年运行维护成本是指为了维持储能电站处于良好的待机状态所需要的费用，一般用固定资产原值和运行维护费率的乘积计算，这里用储能电站的投资费用近似代替固定资产原值，表示为

COM.s=Cinv.sfOM.s

(8)

式中fOM,s为储能的年运行维护费率，通常可取2%。

储能的充放电量损耗表示为

CLoss.s=e(1-ηs)Lcyc_yearWs

(9)

式中：e为电价；ηs表示储能电站充放电循环1次的效率。通常充放电1次，变流器的效率大约为95%，电池的效率大约为90%，整体的充放电效率一般不超过82%～85%。

2.1.2 网络损耗成本

储能在充电和放电时功率流向不同，由此而产生的网络损耗也不同，网络损耗成本的计算如式(10)所示。

(10)

式中Ploss,net,t为典型日各时刻电网的功率损耗，可由潮流计算得到；et为各时刻电价；floss为网损修正系数。

通常，用于输电网分析的潮流计算模型中会将负荷等值到变电站的110 kV侧，因此潮流计算所得的网损不能完全反映电网全部的技术线损情况。为了更准确地反映储能布放位置不同对充电和放电时网络损耗的影响，需要修正这种因网络等值而产生的网损计算结果的偏差。对于没有详细模拟110 kV及以下电压等级的输电网模型来说，修正系数floss表示为

(11)

式中Ploss.110 kV_表示110 kV及以下电压等级技术线损在总技术线损中所占的比例。

2.1.3 弃风成本

弃风成本Closs,w包括两部分，一部分是由于系统调峰能力不足引起的弃风，另一部分是因风电送出通道的阻塞引起的弃风：

(12)

式中：CQF为单位弃风电量成本；PTQF,t为t时刻受调峰约束的弃风功率；PNQF,t为t时刻受网络阻塞约束的弃风功率。

2.2 约束条件

2.2.1 运行约束

主要包括功率平衡约束、节点电压约束、线路功率约束和机组出力约束。

(1)功率平衡约束。

储能放电时的功率平衡约束

(13)

储能充电时的功率平衡约束

(14)

式中：PGi和QGi分别为节点i处电源(含风电机组)的有功和无功出力；Psi为节点i处储能充放电功率；PLi和QLi分别为节点i的有功负荷和无功负荷；Ui为节点i的电压；Gij、Bij和θij分别为节点i和j之间的电导、电纳和相角差。

(2)节点电压约束

Ui,min≤Ui≤Ui,max

(15)

式中Ui,min、Ui,max分别为节点i的电压上下限。

(3)线路输送容量约束

Pi-j≤Pi-j,max

(16)

式中Pi-j、Pi-j,max分别表示节点i和节点j之间线路的功率及其上限。

(4)机组出力约束

PGi,min≤PGi≤PGi,max

(17)

式中PGi,min和PGi,max表示第i台发电机组的最小和最大技术出力。

2.2.2 储能装置约束

(1)充放电量平衡。研究中采用上一节提出的恒功率充放电策略2，即认为储能按照调度指令以日为周期进行充放电，并以相同的功率在低谷时段充电和在高峰时段放电，充放电的时间是相同的。在这种假设条件下，储能的充放电电量平衡约束是自然满足的。

(2)布点数量和单点容量上下限约束。考虑系统中适合安装储能装置的地点有限，且储能电站容量不宜过小和过大。因此储能的布点数量和单个储能装置的容量应满足一定的约束：

Ns·min≤Ns≤Ns·max

(18)

Ps·min≤Ps·n≤Ps·minn=1，2，3，…Ns

(19)

式中：Ns表示储能布点的数量；Ps.n为第n个节点布置的储能电站容量。

3 模型的求解

采用遗传算法对储能容量和布点优化问题进行求解。流程如图2所示，主要步骤如下。

3.1 设定储能电站备选站点

在电网中选择m个储能电站备选点，储能电站的单组容量为Ps0，最大组数为k。则储能电站的容量和布点方案可用变量X表示，X={x1,x2,……,xm}，xi=0表示该点没有储能设备，xi=1表示该点装设1组储能设备，以此类推。

3.2 数据输入

(1)输入储能站的建设成本、运行成本等参数；(2)输入典型日/周/年风电出力曲线、外送功率曲线、负荷曲线以及常规机组出力安排基本计划；(3)输入网架数据，包括线路、变压器等；(4)输入网络中关键断面的定义及其功率限额；(5)设定遗传算法最大进化代数。

3.3 构建方案评价子函数

构建储能方案的评价子函数C=F(X)，该评价函数即为优化问题的目标函数，X表示储能的容量和布点方案。步骤如下：

(1)由输入储能方案及其他负荷、发电数据，构建各个时刻的直流潮流计算数据；

(2)执行近似考虑网络损耗的直流潮流计算(将损耗分摊在支路两端节点上)；

(3)如果平衡机出力越限，则将其越限功率差额在指定机群内进行分担，若其机组已无调整空间，则将越限功率偏差认定为调峰不足功率；

(4)如果风电外送断面功率超过限值，则在指定风电场采取弃风措施；

(5)重复进行(2)、(3)、(4)，直至直流潮流收敛；

(6)记录该储能方案下各个时刻的调峰不足弃风功率以及由于网络阻塞产生的弃风功率；

(7)由式(2)计算评价函数C=F(X)。

3.4 采用遗传算法求解该优化问题

主要步骤为：

(1)随机生成第1代个体，对每个个体计算其评价函数C=F(X)；

(2)对个体进行随机排序；

(3)相邻个体两两进行交叉，形成新个体，并对新个体计算评价函数值；

(4)对随机选择个体进行随机染色体位置随机变异，新个体计算评价函数值；

(5)在新的个体与原父辈个体组成的集合中进行筛选，删除劣质个体，保持每一代个体总数不变；

(6)重复执行(2)、(3)、(4)、(5)，直至达到最大进化代数。

图2 储能容量和布点优化模型求解流程图Fig.2 Solution process of energy storage and location optimization model

4 算例分析

以IEEE RTS79系统为例对上述模型和求解方法进行验证。为使算例系统更符合研究场景，在算例系统中接入了400 MW的风电场，其中节点17和节点18各接入200 MW风电。为验证所提方法对解决风电送出通道网络阻塞问题的有效性，假设节点17处风电场汇集站容量为135 MVA。网络接线图及风电场接入位置见图3，机组类型及其出力限值如表1所示。

IEEE RTS79算例系统提供了年负荷特性，风电出力特性参考我国甘肃某风电场2013年实测出力数据。系统调峰压力最大日的等效负荷曲线如图4所示。

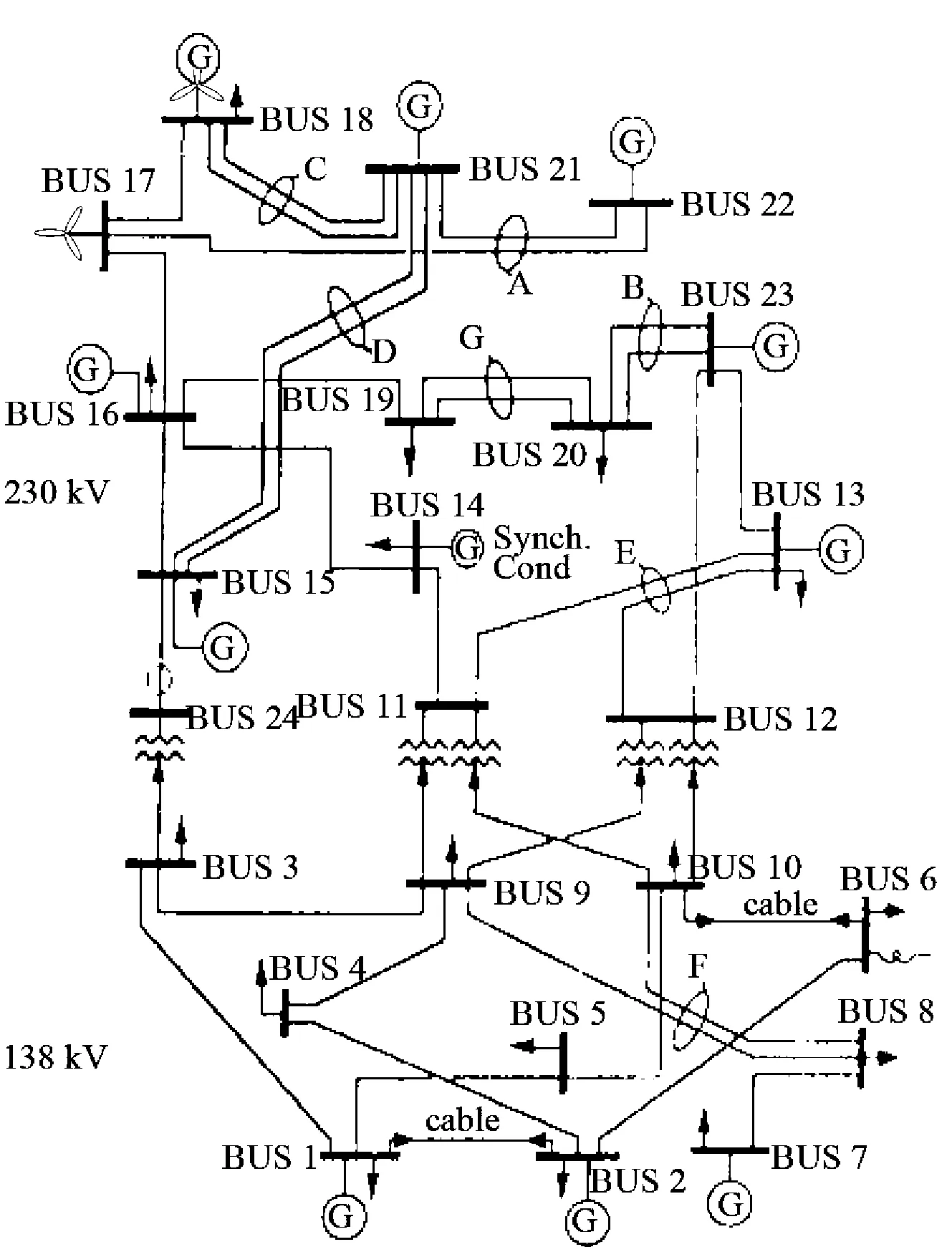
图3 IEEE-RTS79系统结构图Fig.3 Structure of IEEE RTS79 system表1 常规发电机组出力限值Table 1 Output limit of conventional generators

MW

选择风电场送出端(节点17、18)以及负荷集中的枢纽变电站(节点9、10、19)为储能电站备选点，设定储能装置单组容量为10 MW，最大组数为4组，采用本文所提出的恒功率充电策略2，恒功率持续运行时间为3 h。充电策略如图5所示。

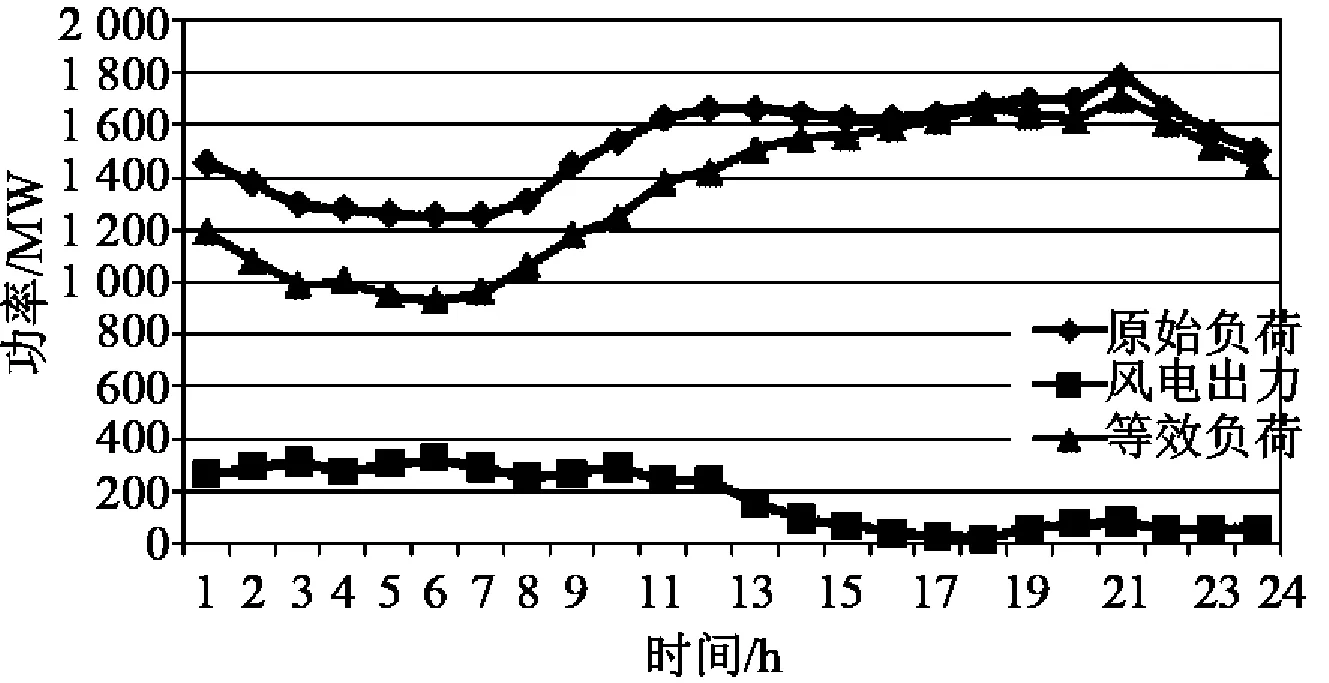
图4 调峰压力最大日负荷曲线Fig.4 Daily load curve with the maximum peak regulation pressure

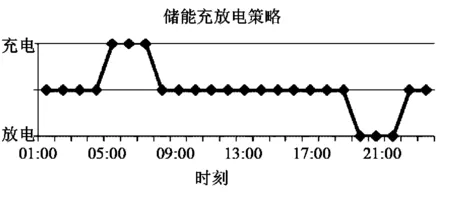
图5 储能充放电策略Fig.5 Charging and discharging strategy of energy storage

利用所提优化模型对储能的容量和布局进行优化计算。对算例系统而言，若按风电平均上网电价0.56元/( kW·h)计算弃风电量损失，则安装储能以减少弃风是不经济的。考虑到风力发电过程可近似认为没有碳排放，因此考虑风电的碳减排效益后弃风损失约为0.65元/( kW·h)[15]，对储能容量和布点进行优化计算。筛选最优的3个方案如表2所示。

由计算结果可以看出，典型日下，无储能时系统总弃风率为4.72%，其中由于风电送出通道受阻引起的弃风率为2.5%，由于调峰能力不足引起的弃风率为2.21%。根据优化计算结果，需要装设40 MW储能设备，其中风电送出端的节点17和负荷中心的节点10各装20 MW。在选定的储能充放电策略下，算例系统的弃风率降至1.78%，减少了62.3%的弃风电量，其中网络受阻引起的弃风率降至1.07%，调峰限制引起的弃风率降至0.71%。

表2 储能优化配置方案

Table 2 Optimization configuration scheme of energy storage

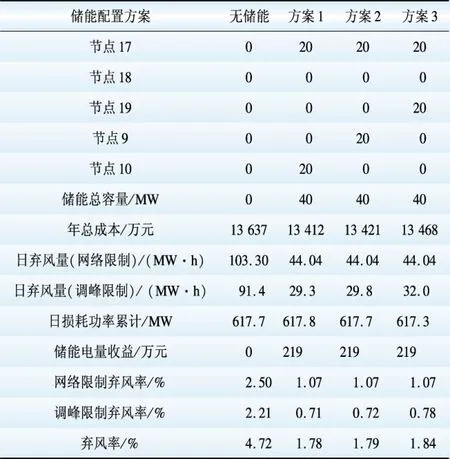
由于考虑了通道输电能力对风电送出的限制，在风电送出通道的送端加装储能设备，在风电出力高峰时充电，在风电出力较低时放电，通过对储能位置的优化既能缓解系统调峰能力不足引起的弃风问题，又能兼顾风电送出通道的阻塞问题。

5 结 论

针对大规模风电并网地区调峰能力不足引起大量弃风问题，本文提出采用大容量电池储能技术的“削峰填谷”功能提高系统调峰能力减少弃风损失的3种实用的充放电策略。基于所提出的储能的恒功率充放电策略研究了储能电站容量和布点的优化方法。该方法既考虑了系统调峰能力不足引起的弃风，又能兼顾风电送出通道阻塞引起的弃风损失。结合我国甘肃实际风电出力特性对IEEE RTS79系统进行储能布局优化分析，验证了方法的有效性。随着大容量储能技术的进一步完善，储能电站投资费用将进一步降低，应用该方法能够为解决大规模风电并网地区的弃风问题提供技术解决方案。

[1]李军徽.抑制风电对电网影响的储能系统优化配置及控制研究[D].北京：华北电力大学, 2012. LI Junhui. Research on the optimaland control of energy storage system to reduced the effect of wind power on the grid[D]. Beijing: North China Electric Power University, 2012.

[2]张宁，周天睿，段长刚，等.大规模风电接入对电力系统调峰的影响[J].电网技术，2010，34(1)：152-158. ZHANG Ning，ZHOU Tianrui，DUAN Changgang，et al.Impact of large-scale wind farm connecting with power grid on peak load regulation demand[J].Power System Technology，2010，34(1)：152-158.

[3]朱凌志，陈宁，韩华玲.风电消纳关键问题及应对措施分析[J].电力系统自动化，2011，35(22)：29-34. ZHU Lingzhi，CHEN Ning，HAN Hualing.Key problems and solutions of wind power accommodation[J].Automation of Electric Power，2011，35(22)：29-34.

[4]胡娟，杨水丽，侯朝勇，等.规模化储能技术典型示范应用的现状分析与启示.电网技术，2015，39(4)：879-885. HU Juan，YANG Shuili，HOU Chaoyong，et al.Present condition analysis on typical demonstration application of large-scale energy storage technology and its enlightenment[J].Power System Technology，2015，39(4)：879-885.

[5]许守平，李相俊，惠东.大规模电化学储能系统发展现状及示范应用综述[J].电力建设，2013，34(7)：73-80. XU Shouping，LI Xiangjun，HUI Dong.A review of developent and demonstration application of large-scale electrochemical energy storage[J].Electric Power Construction，2013，34(7)：73-80.

[6]王承民，孙伟卿，衣涛，等.智能电网中储能技术应用规划及其效益评估方法综述[J].中国电机工程学报，2013，33(7)：33-41. WANG Chengmin，SUN Weiqing，YI Tao，et al.Review on energy wtorage application planning and benefit evaluation methods in smart grid[J].Proceedings of the CSEE，2013，33(7)：33-41.

[7]王成山，于波，肖峻，等.平滑可再生能源发电系统输出波动的储能系统容量优化方法[J].中国电机工程学报，2012，32(16)：1-8. WANG Chengshan，YU Bo，XIAO Jun，et al.Sizing of Energy Storage Systems for Output Smoothing of Renewable Energy Systems[J].Proceedings of the CSEE，2012，32(16)：1-8.

[8]廖强强，陆宇东，周国定，等.基于削峰填谷的钠硫电池储能系统技术经济分析[J].电力建设，2014，35(4)：111-115. LIAO Qiangqiang，LU Yudong，ZHOU Guoding，et al.Technical and economic analysis on NaS battery energy storage system based on peak shaving[J].Electric Power Construction，2014，35(4)：111-115.

[9]郑乐，胡伟，陆秋瑜，等.储能系统用于提高风电接入的规划和运行综合优化模型[J].中国电机工程学报，2014，34(16)：2533-2543. ZHENG Le，HU Wei，LU Qiuyu，et al.Research on planning and operation model for energy storage system to optimize wind power integration[J].Proceedings of the CSEE，2014，34(16)：2533-2543.

[10]修晓青，李建林，惠东.用于电网削峰填谷的储能系统容量配置及经济性评估[J].电力建设，2013，34(2)：1-5. XIU Xiaoqing，LI Jianlin，HUI Dong.Capacity configuration and economic evaluation of energy storage system for grid peak load shifting[J].Electric Power Construction，2013，34(2)：1-5.

[11]严干贵，冯晓东，李军徽，等.用于松弛调峰瓶颈的储能系统容量配置方法[J].中国电机工程学报，2012，32(28)：27-35. YAN Gangui，FENG Xiaodong，LI Junhui，et al.Optimization of energy storage system capacity for relaxing peak load regulation bottlenecks[J].Proceedings of the CSEE，2012，32(28)：27-35.

[12]唐文左，梁文举，崔荣，等.配电网中分布式储能系统的优化配置方法[J].电力建设，2015，36(4)：38-45. TANG Wenzuo，LIANG Wenju，CUI Rong，et al.Optimal allocation method of distributed energy storage system in distribution network[J].Electric Power Construction，2015，36(4)：38-45.

[13]靳文涛，马会萌，谢志佳.电池储能系统平滑风电功率控制策略[J].电力建设，2012，33(7)：7-11. JIN Wentao，MA Huimeng，XIE Zhijia.Wind power smoothing control strategy of battery energy storage system[J].Electric Power Construction，2012，33(7)：7-11.

[14]陈满，陆志刚，刘怡，等.电池储能系统恒功率削峰填谷优化策略研究[J].电网技术，2012，36(9)：232-237. CHEN Man，LU Zhigang，LIU Yi，et al.Research on optimal peak load shifting strategy of battery energy storage system operated in constant power mode[J].Power System Technology，2012，36(9)：232-237.

[15]段建民，王志新，王承民，等.考虑碳减排效益的可再生电源规划[J].电网技术，2015，39(1)：11-15. DUAN Jianmin, WANG Zhixin, WANG Chengmin，et al. Renewable power planning considering carbon emission reduction benefits[J].Power System Technology，2015，39(1)：11-15.

(编辑 刘文莹 )

Study on Energy Storage Capacity and Layout Optimization by Reducing Wind Power Curtailment Loss

WU Junling, ZHANG Yantao, QIN Xiaohui, LIANG Caihao

(China Electric Power Research Institute, Beijing 100192, China)

According to the wind power curtailment problem caused by the shortage of peak regulation capacity of power system with large-scale wind power integration in China, this paper proposes the charging and discharging strategy of energy storage battery with large capacity to improve the peak regulation capacity and reduce the wind power curtailment loss. Based on the proposed energy storage constant power charging and discharging strategy, we establish a mathematical model for capacity and layout optimization of energy storage power plants, and adopt genetic algorithm to solve the model. This model takes the minimum total costs as optimization objectives including the investment and operation costs of energy storage power plant, network loss, and the sum of wind power curtailment caused by the shortage of peak regulation capacity and wind power channel blocking.It also considers the benefits resuled from the electricity price gap between peak and valley periods and the benefits of carbon emission reduction of wind power, and meets the security operation constraints of power grid as well. Finally, we use IEEE RTS79 system to analyze the layout optimization of energy storage and verify the effectiveness of the method. The application of this method can provide technical solution scheme for the wind power curtailment problem in the area of large-scale wind power integration.

wind power curtailment; battery energy storage; optimization; genetic algorithm

国家电网公司科技项目 (XT71-13-032)

TM 721

A

1000-7229(2016)06-0024-07

10.3969/j.issn.1000-7229.2016.06.004

2016-04-01

吴俊玲(1978)，女，硕士，高级工程师，主要研究方向为电网规划、电力系统分析及新能源发展；

张彦涛(1980)，男，硕士，高级工程师，主要研究方向为电网规划、电力系统分析及全球能源互联网；

秦晓辉(1979)，男，博士，高级工程师，主要研究方向为电网规划、电力系统分析、半波长输电技术；

梁才浩(1978)，男，博士，高级工程师，主要研究方向为电网规划、新能源发展及全球能源互联网。