面向能源互联网的新型需求侧管理模式研究
2016-02-16刘道新郭万祝王世成曾鸣
刘道新,郭万祝,王世成,曾鸣,3
(1.华北电力大学经济与管理学院,北京市 102206;2. 国网冀北电力有限公司秦皇岛供电公司,河北省秦皇岛市 066000;3.新能源电力系统国家重点实验室(华北电力大学),北京市 102206)
面向能源互联网的新型需求侧管理模式研究
刘道新1,郭万祝2,王世成1,曾鸣1,3
(1.华北电力大学经济与管理学院,北京市 102206;2. 国网冀北电力有限公司秦皇岛供电公司,河北省秦皇岛市 066000;3.新能源电力系统国家重点实验室(华北电力大学),北京市 102206)
目前,能源互联网已经成为我国电力系统发展的主要方向。能源互联网的建设将在很大程度上改变目前能源利用现状和管理模式。从需求侧管理的角度,阐述能源互联网条件下的新型控制策略,传统的需求侧管理是基于电网与用户的相互作用,通过相关协议达到对负荷的部分可控,能源互联网的发展,使得用户侧的信息交互更加重要与频繁,同时由于各种能源发电形式的接入,使得对用户的负荷管理也越来越重要。提出一种面向能源互联网的需求侧管理方法,该方法利用用户侧健全的通讯基础设施,在每个用户的智能量测设备中增加用电计划控制模块,该模块借助博弈论的思想使每个用户根据其他用户的用电计划制定出使得自己用电支出最小的用电计划,最终得到所有用户的能源消费计划。在整体的能源消费计划下,达到系统运行的峰均比和发电成本最小。最后,通过实例仿真证明了该负荷管理模式的有效性。
能源互联网;用电计划控制;博弈论;峰均比最小
0 引 言
需求侧管理是电力部门通过一定的手段管理用户负荷的一种方式,以达到系统运行最优。需求侧管理能够充分利用现有电源,减少系统装机容量和输配电设施,提高设备利用率和用电效率。对于未来能源互联网,由于电网和通讯设备的互联为电动汽车的接入提供了大量的接口,电动汽车作为新兴柔性负荷在电网运行过程中将扮演重要的角色,另外各种间歇式发电单元的接入,给电网的稳定运行带来了挑战[1-3],有效的控制负荷,减小系统的备用容量,降低运行的峰均比是能源互联必须解决的问题。
能源互联网的构建不仅仅是灵活的电力网络,更重要的是它将实现电力流与信息流的一体化平台建设。这为新型的需求侧管理策略的实现提供了物理基础。目前关于需求侧负荷管理,研究较多的是直接负荷控制[4-7],通过供电企业与用户、工厂企业等达成供用电协议,供电部门按照协议对用户的部分用电设备进行远程控制。比如,在负荷高峰时段,供电部门就会根据事先达成的协议切出用户的供热、制冷、照明等设备。虽然可以解决削减峰值负荷的问题,但是对于居民用户而言,直接负荷管理将影响居民正常生活,他们很难积极主动参与到直接负荷控制的管理中来,并且有可能导致用户的信息泄露。
另一种需求侧负荷管理措施是利用电价机制,即通过调节电价鼓励用户主动管理自身负荷,以在峰值负荷时主动削减负荷[8-10]。电价模式分为峰谷电价、分时电价和实时电价。对于实时电价协议,1天内不同时间段的电价是不同的。通常根据用电需求,夏天午后及冬天晚上的电价较高。但是,这种电价机制同样会引起一些问题,用户通常很难对电价的变化及时作出用电的调整,并且需要用户实时关注电价的波动,实时改变自己的用电计划,这给用户带来了诸多不便。另外,这种电价机制的调节对用户而言具有趋同的特性,可能出现将峰值负荷整体转移到非峰值负荷处的情况,实际并不会有效降低峰均比。
对于电网来说,其实际关注的并不是每一个用户的用电负荷,而是某一具体时段内所有用户的总负荷。因此,为了达到一个区域的负荷可控,本文提出利用未来能源互联网完善的通讯系统,在用户之间建立信息交互,通过用户之间的信息交互,在用户之间形成一种博弈关系,从而使最终整个区域内负荷可控。
本文提出一种适应于未来能源互联网需求侧管理的用户用电计划自动调整机制。在某一供电区域的用户都安装自动用电计划控制器。用户用电控制器作为一种控制设备安装在家庭的智能量测表内,并且通过通讯设备实现区域内各用户的互联。用电计划控制器通过执行分布寻优算法自动为每一个用户制定出节能的用电计划,算法的目标函数是系统整体运行的网损最小。用户之间借助博弈论[11-14]的思想进行分析,通过适当的电价机制激励用户参与博弈,使得最终纳什平衡达到系统运行最优。
1 系统模型
1.1 系统负荷模型
与大电网连接的供电区域如图1所示,假设每个用户都装有智能电表,并且智能电表内都装设有用电计划控制器。智能电表与电力线和局域网络相连。电网与用户及用户之间的信息都通过局域网的通讯协议进行交互。
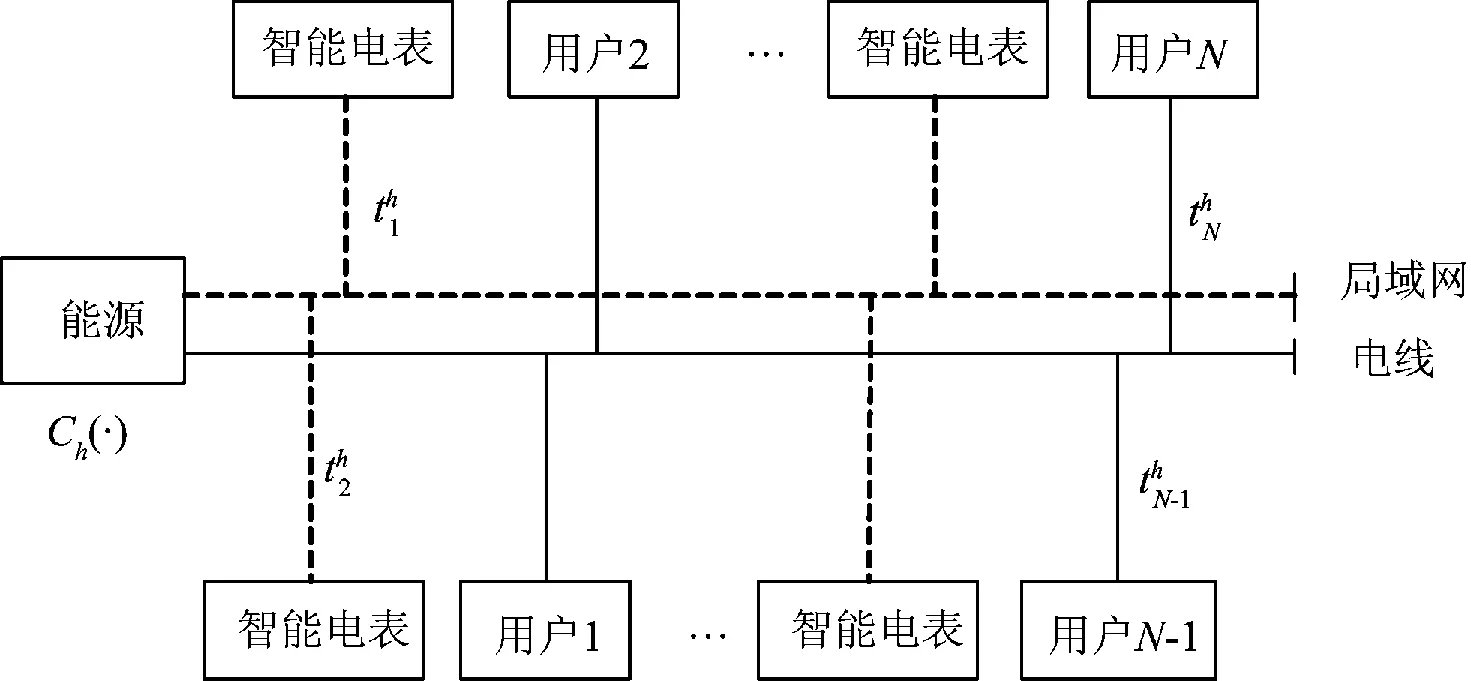
图1 用户信息流Fig.1 Flow of user’s information
图中:N代表上述系统的用户集合;n表示用户集合中的第n个用户;h表示1天中第h个时段;H表示1天的用电时段数,通常设H=24,用电时段是等间隔的;对于任一个用户,用L表示第n个用户第h小时的负荷;则1天中第h个时段所有用户的总负荷可表示为
(1)
1天中峰值负荷可表示为
(2)
均值负荷表示为
(3)
负荷率为
(4)
1.2 费用函数
这里定义Ch(Lh)表示第h时段的电源发电所需要的费用。通常,同样的负荷在不同的时段发电所用的费用是不同的。另外,这里假设Ch(Lh)满足如下条件。
(1)费用函数是递增的。对于任意h,满足下面不等式:
Ch(Lh1)≤Ch(Lh2),Lh1≤Lh2
(5)
从式(5)可以看出发电费用随着负荷的增加而增加。
(2)费用函数必须是凸函数。即对于任意的Lh,都存在:
(6)
满足条件(1)、(2)的典型费用函数如下:
(7)
1.3 用户负荷描述
对于任意n∈N,用An表示用户n的所有电气设备,包括电动汽车、冰箱、洗衣机、空调等。对于任意a∈An,定义一个能源的消费计划,用下面的向量表示:
(8)
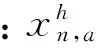
(9)
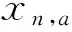
(10)
由此,则系统中所有设备24 h的用电负荷总负荷可表示为
(11)
通常有些用电设备的用电量是不能转移的,在这种情况下用电计划控制器并不对这些设备进行优化控制,具体如图2所示。
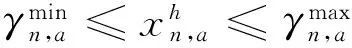
(12)

图2 用电计划控制器Fig.2 Controller of energy plan
2 优化模型
2.1 峰均比最小
由之前的描述可将峰均比表示如下:
(13)
通过上文的叙述,通过调整用户用电计划从而使得εPA最小,即
(14)
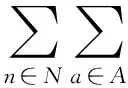
(15)
接着引入变量Γ,将上式变为
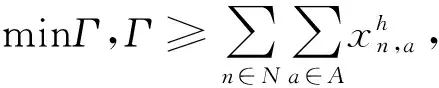
(16)
式(16)可以用内点法处理。通过分析可知用电方案并不唯一。当εPA相同时,可以存在不同的用电计划。
2.2 发电费用最小
所有用户的用电计划除了使得εPA最小外,还需要使得系统总的发电费用最小。总发电费用可以用式(17)来表示:
(17)
这个优化的目标函数是凸函数,可以由凸函数的解法得到解决,并且凸函数仅有一个最优解。
3 能源消费博弈
最小化问题虽然可以通过上述方法得到解决,但是由于系统的运行状态是变化的,因此希望得到一种能随系统的运行状态而自动更新用电计划的方法。通过利用能源互联网完善的通讯设备进行用户之间的信息交互,采用一种分布式的算法实时更新用户的用电计划。目标是让智能量测设备制定出用电计划安排。分布式计算以系统的发电费用最小为目标函数。
3.1 价格协议
对于用户n用bn表示每天用户需要支付给电网公司的费用。而电价应该和用户一天所用电量和总的发电成本有关。假设满足如下条件:
(18)
式(18)左边表示用户一天总的支付费用,右边表示一天总的发电成本。为了便于比较定义:
(19)
如果k=1表示收支预算平衡,也就是说电网向用户收取的费用和成本相同。另一方面,如果k大于1,用户的总支出和电网总成本的差值就是电网的利润值。另外假设

(20)
也就是说用户支出的费用和用电量成正比。比如说用户n的用电量是用户m用电量的2倍,则用户n的费用将是用户m的2倍。收费的准确数值取决于该时段的发电的成本C,由式(7)表示。尽管式(20)确立了用户用电支付与发电成本之间的联系,但同时用户的支付费用和该时段的电价也有很大的联系。通过将式(20)变形可以得到:
(21)
由式(9)、(10)、(19)、(20)可得:
(22)
式中:
(23)
从式(22)中我们可以看出用户n的用电费用和m紧密相关,因此就建立用户之间的博弈关系。
3.2 博弈模型
由于每个用户的用电费用都和其他用户的用电计划相关,自然会导致在用户间引起博弈关系。
博弈的参与者:一个区域内所有的用户。
博弈策略:每个用户通过制定用电计划向量Xn,最大化各自的收益。
博弈收益:
(24)
式中x-n=[x1,…,xn-1,xn+1,…xN]表示出了用户n之外的所有其他户的向量。基于以上定义,用户将会安排自己的用电计划使得自己支付给供电公司的费用最少。关于博弈论的定理这里不再赘述。
4 分布式算法
区域的所有用户都参与到用电计划控制单元,通过用户间信息的交互可以实现用户用电计划的自动更新,使得每个用户的用电费用最小。并且可以证明用户之间的纳什均衡的解与系统全局最优解是相同的。在系统运行过程中要通过各控制器的分布式算法来实现。
4.1 程序流程
对于任意一个用户n,假设其他n-1个用户的用电计划是固定的。用户n的用电计划的最佳策略将通过求解下面的式子得到解决:
(25)
这里,式(25)得到的解为局部最优解,因为优化的结果仅仅是得到用户n的最佳用电计划。因为Ωn是固定的,其值不依赖于Xn,则式(25)可以由式(26)表示:
(26)
注意到式(26)和式(17)具有同样的目标函数。然而,式(26)仅仅有用户n的局部变量。更重要的是式(26)是凸函数,可以由内点法得到解决。只要用户n知道1天所有时段的成本函数Ch和包含所有其他用户用电计划的向量L-n=[l1,…,ln-1,ln+1,…,lN],就可以解决式(26)的问题,这里采用分布式算法。
其计算流程如下:
(1)初始化Ln和L-n;
(2)用内点法解式(26);
(3)根据新解更新xn;
(4)将用户n的Ln通过通讯设备发送到其他用户;
(5)判断是否收敛,若不收敛转到(2);
(6)是否收到其他用户的改变信息,更新L-n;
(7)结束;
(8)跳转到下一用户。
计算的第1步进行数据初始化,对于用户n而言随机假设lm的状态,因为初始状态时用户n并不知道其他用户的状态。第2步到第7步具体执行此算法直到结果收敛。每一个用电计划控制器都用内点法根据自己得到的其他用户的用电计划进行计算。每个用户的结果都是使得各自利益最大化的局部最优解,然后将计算出的用电计划发送出去,供其他用户参考。在图2上看到交互的信息就是由此算法执行发送的,具体的通讯协议是通过局域网来实现。并且交互的信息仅仅是用户用电的总负荷并不涉及具体的用电设备的用电,因此不会导致用户私人信息的泄露。
这里所叙述的负荷控制策略与传统的负荷管理策略有很大不同。首先,不像直接负荷管理,这种策略的用户完全可以自己控制自己的用电设备。因此,用户的私人信息不会泄露。更重要的是用户仅需要根据得到的信息制定出符合自己利益的用电计划即可。这种管理策略基于图2所示的结构框架。
4.2 收敛性和最优解特性
这一部分将证明这种分布式算法的收敛性和最优解特性。评估的基础是根据下面的博弈定理:
如果用户之间的个人用电消费计划更新是不同步的,没有任何2个用户的用电计划更新是同时的,对于用电计划的博弈来说,无论从任何一个点开始执行,算法都最终收敛于一个固定的点。该定理的证明式不再赘述。
该定理充分地证明了算法的收敛性。仅仅要求用户按照次序更新各自的用电计划即可。比如,通过检测用户更新用电计划的时间,只有用户n收到命令轮到其更新用电计划时,用户n才执行程序(2)到(7)。由于在更新次序上的限制,可以保证算法可以自动收敛到全局最优解。另外,如果所有用户的用电计划在24 h内均不发生更改,则此算法就是长时间尺度的优化运行算法;如果需要用户的用电计划不断地更改,则此算法就成了实时优化运行算法。
5 算例分析
本节通过仿真算例分析评估算法的性能,假定这里有20个用户都安装有用电计划控制器。每个用户都有15~25个不可控制的负荷,这些负荷不参与用电计划安排。同样还包括15~20个可控负荷,称之为柔性负荷。这些柔性负荷可以由用电计划控制器安排用电。通常这些柔性负荷包括:洗衣机(日耗能1.8 kW·h),电动汽车(日耗能12 kW·h),烘干机(2.7 kW·h)。在仿真模型中假设每个用户都是随机的使用柔性负荷和不可控负荷,同样也要考虑到晚间负荷较夜间负荷大。例如,假设电动汽车在午后和次日早上前充电是合理的。为了简便发电费用方程如公式(7)所示,且令bh=ch=0,在白天早上9点到晚上12点ah=0.3,从晚上12点到早上9点ah=0.2。假定系统的预算平衡即令k=1。算法在一种单循环模式下运行,在这个模式下,当轮到用户n时,用户n开始执行此程序,从而更新自己的用电计划,并且随后通知其他用电计划的更改。接着随机地跳转到另外其他的用户继续执行此程序,直到程序收敛。通过这种方法保证了每次仅有1个用户进行用电计划更新。
5.1 性能比较
总的用电消费计划和总的发电成本仿真结果如表1、表2所示。表1表示没有用电计划控制器的仿真结果,表2表示有用电计划控制器的结果。
表1 未装设控制器各时段用电量统计表
Table 1 Statistics of power consumption without controller kW·h

表2 装设控制器各时段用电量统计表Table 2 Statistics of power consumption with controller kW·h
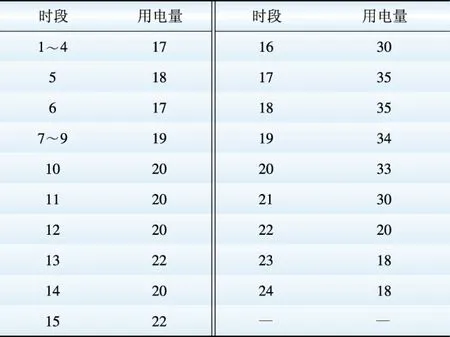
对于没有用电计划控制器的案例,假定每个用户的用电设备a在其用电区间内按照典型的功率水平运行。对于安装有用电计划控制器的案例,其设备的运行时间和功率水平均由算法的运算结果给出。通过比较表1和表2,可以发现没有控制器设备的案例,其峰均比为3.6。而装有控制器的峰均比为2.05,并且后者每个小时的负荷较前者更加均匀。可见,虽然每个用户的总负荷相同,但是由于控制器的安排使得系统运行更为高效。另一方面,算法的迭代过程如图3所示。可见算法迭代到10次时收敛,基本上是每个用户迭代2次即可达到全局最优。

图3 收敛曲线Fig.3 Convergence curves
5.2 用户支出与峰均比
分布式算法不但可以使得系统的发电费用和峰均比最小,同样也对用户有利。
图4比较了单个用户的峰均比和总体用户的峰均比。其中,如图4可知最大的εPAR可达到4.0,但总体的εPAR仅有2.05,对于每个用户的峰均比用下面的公式计算:
(27)

图4 用户与系统峰均比Fig.4 Peak-average ratio of users and system
从图4中可以看到整体调节后的峰均值小于单个用户的峰均比。并且有些用户的峰均比特别的高。这也印证了之前所讨论的电网实际上关心的并不是每个用户的用电状态,而是用户整体的用电情况。
6 结 论
本文提出一种基于能源消费计划的自动优化模型,以实现面对未来能源互联网条件下对负荷的有效管理。该模型能够使得系统运行的发电费用最小,同时降低运行的峰均比。基于博弈论的思想对用户用电计划进行建模,使得用户积极参与到负荷调节中来,并且实现用户的用电费用最小。本文提出的需求侧管理模型是基于能源互联网通讯基础设施完善的条件下,用户之间完善的信息交互,使得用户之间进行博弈,各个用户根据其他用户的用电计划情况,计算出自己的用电计划。所有用户用电计划的集成就构成了整体的能源消费计划,整体的能源消费计划能够满足配网运行的峰均比最小及总发电费用最小。仿真结果也表明,分布式的优化算法不仅可以使得各个用户受益,同时能有效地达到电网对负荷的有效控制。另外,本文没有考虑用户侧储能的情况,比如用户的电动汽车可以作为储能元件向系统回馈能量,参与系统的优化运行,因此今后可以考虑用户侧系统回馈能量时的负荷管理模式。
[1]刘开俊.能源互联网发展路径探究[J].电力建设,2015,36(10):5-10. LIU Kaijun.Development path exploration of energy internet[J].Electric Power Construction,2015,36(10):5-10.
[2]赵海,蔡巍,王进法,等.能源互联网架构设计与拓扑模型[J].电工技术学报,2015,30(11):30-36. ZHAO Hai,CAI Wei,WANG Jinfa,et al.An architecture design and topological model of intergrid [J].Transactions of China Electrotechnical Society,2015,30(11):30-36.
[3]王继业,孟坤,曹军威,等.能源互联网信息技术研究综述[J].计算机研究与发展,2015,52(5):1109-1126. WANG Jiye,MENG Kun,CAO Junwei, et al.Information technology for energy internet: a survey[J].Journal of Computer Research and Development,2015,52(5):1109-1126.
[4]NERC. Potential reliability impacts of emerging flexible resources[R].American:The North American Electric Reliability Corporation,2010.
[5]曹军威,杨明博,张德华,等.能源互联网——信息与能源的基础设施一体化[J].南方电网技术,2014,8(4):1-10. CAO Junwei,YANG Mingbo,ZHANG Dehua,et al.Energy internet:an infrastructure for cyber-energy integration[J].Southern Power System Technology,2014,8(4):1-10.
[6]HIRST E,CAVANAGH R,MILLER P.The future of DSM in a restructured US electricity industry [J].Energy Policy,1996,24(4):303-315.
[7]STADLER I.Power grid balancing of energy systems with high renewable energy penetration by demand response[J].Utilities Policy,2008,16(2):90-98.
[8]王蓓蓓,李扬.面向智能电网的电力需求侧管理规划及实施机制[J].电力自动化设备,2010,30(12):19-24. WANG Beibei,LI Yang.Demand side management planning and implementation mechanism for smart grid [J].Electric Power Automation Equipment,2010,30(12):19-24.
[9]曹培,翁慧颖,俞斌,等.低碳经济下的智能需求侧管理系统[J].电网技术,2012,36(10):11-16. CAO Pei,WENG Huiying,YU Bin,et al.Research on smart demand side management system in low-carbon economy[J].Power System Technology,2012,36(10):11-16.
[10]SWISHER J,DE MANINO G,REDLINGER R.Tools and methods for integrated resource planning-improving energy efficiency and protecting the environment[J].Utilities Policy,2013(10):11-16.
[11]中国赴欧洲电力需求侧管理培训团.欧洲电力需求侧管理对中国的启示(上)——来自中国赴欧洲电力需求侧管理的培训报告[J].电力需求侧管理,2007,9(2):1-6. Chinese Group to European DSM Training.Enlightenment of European DSM to China——Report from Chinese group to European DSM training[J].Power Demand Side Management,2007,9(2):1-6.
[12]卢强,陈来军,梅生伟.博弈论在电力系统中典型应用及若干展望[J].中国电机工程学报,2014,34(29):5009-5017. LU Qiang,CHEN Laijun,MEI Shengwei.Typical applications and prospects of game theory in power system[J].Proceedings of the CSEE,2014,34(29):5009-5017.
[13]王梅霖.电力需求侧管理研究[D].北京:北京交通大学,2011. WANG Meilin.Research on demand side management[D].Beijing:Beijing Jiaotong University,2011.
[14]HUANG Y H,ZHOU X X.Knowledge model for electric power big data based on ontology and semantic web[J].CSEE Journal of Power and Energy Systems,2015,1(1):19-27.
(编辑 张媛媛)
New Demand-Side Management Pattern for Energy Internet
LIU Daoxin1, GUO Wanzhu2, WANG Shicheng1, ZENG Ming1,3
(1.School of Economics and Management, North China Electric Power University, Beijing 102206, China;2. State Grid Jibei Electric Power Company Qinhuangdao Electric Power Company, Qinhuangdao 066000,Hebei Province, China; 3. State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources (North China Electric Power University), Beijing 102206, China)
At present, the energy Internet has become the main development direction of power system in our country. The construction of the energy Internet will change the energy utilization status and the management pattern. In the perspective of demand side management, this paper studies the new control strategy under energy Internet. Traditional demand side management controls parts of the load by related protocol based on the interaction between the grid and the users. The development of energy Internet makes the information interaction between users more important and frequently. At the same time, the access of various generation forms of energy makes the demand side management more important. This paper proposes a new demand side management method for energy Internet, which uses the user-side sound communications infrastructure to add the power control module in the intelligent measurement equipment for each user. Through the game theory in this module, each user makes his energy plan according to those of other users which make his payment minimum, so as to obtain all the user’s energy consumption plans, and realize the minimum peak-average ratio of system operation and power generation cost under the overall energy consumption plan. At last, the example simulation results prove the validity of the load management mode.
energy Internet; energy plan control; game theory; the minimum peak-average ratio
中央高校基本科研业务费专项资金资助项目(2015QN01)
TM 727; F 426.61
A
1000-7229(2016)06-0010-07
10.3969/j.issn.1000-7229.2016.06.002
2016-03-21
刘道新(1970),男,博士研究生,高级工程师,研究方向为电力统计管理、电力技术信息化;
郭万祝(1970),男,工程师,研究方向为电力需求侧管理及电力营销;
王世成(1988),男,博士研究生,研究方向为电力经济管理;
曾鸣(1957),男,教授,博士生导师,主要从事电力市场与技术经济研究工作。
Project support by Fundamental Research Funds for the Central Universities(2015QN01)
