基于改进果蝇优化算法的分布式电源优化配置

2016-02-16关添升王琦刘赫郑媛李德鑫刘亚东潘超

电力建设 2016年6期

关添升，王琦，刘赫，郑媛，李德鑫，刘亚东，潘超

(1.国网吉林省电力有限公司培训中心，长春市 130062；2.中国电力工程顾问集团东北电力设计院有限公司，长春市 130021；3.国网吉林省电力有限公司电力科学研究院，长春市 130021；4.吉林工程职业学院，吉林省四平市 136001；5.东北电力大学电气工程学院，吉林省吉林市 132012)

关添升1，王琦2，刘赫3，郑媛4，李德鑫3，刘亚东3，潘超5

研究分布式电源(distributed generation，DG)接入配电网的优化配置问题，基于模糊隶属度技术建立综合考虑投资效益、电压指标和网损的多目标优化配置模型，有效解决了因各子目标数量级不同而导致的过度优化问题。对一种新颖的仿生智能算法——果蝇优化算法(fruit fly optimization algorithm，FOA)进行改进，效仿细菌在觅食过程中的趋化思想，在算法寻优过程中引入吸引和排斥操作，有效提高了种群多样性，降低了算法陷入局部最优的可能。IEEE 33节点系统的仿真结果表明，与传统果蝇优化算法和粒子群优化算法(particle swarm optimization，PSO)相比，改进果蝇优化算法(improved fruit fly optimization algorithm，IFOA)在寻优速度和求解精度上都具有较大优势，能快速、有效地搜索到最优配置方案，从而验证了改进算法的有效性与合理性。

改进果蝇优化算法(IFOA)；配电网；分布式电源(DG)；多目标优化；综合隶属度

0 引言

分布式电源(distributed generation，DG)作为未来能源战略结构的重要组成部分，以低污染、安装方式灵活多变和便于维护等优点获得了国内外的广泛关注，并得到了迅速的发展[1]。但大规模DG接入配电网，对配电网的规划、运行和保护提出了更高的要求和挑战[2-4]。DG的合理优化配置将有助于降低网络损耗、改善电压质量和提高系统负荷率；若配置不合理将适得其反，甚至会出现电压质量恶化、功率倒流、系统安全性降低等一系列问题[5-6]。因此，研究DG在配电网中的优化配置问题具有重要的理论价值和现实意义。

含DG的配电网优化配置问题已成国内外的研究热点，目前已取得了一定的进展。文献[7]建立了有功网损最优的DG单目标规划模型，将电压约束以罚函数的形式纳入目标函数，采用改进粒子群算法对模型求解，但未考虑DG投资效益对规划结果的影响。文献[8]建立了综合考虑DG单位投资效益和其接入后改善电网收益的多目标规划模型，采用改进非劣解排序遗传算法对问题求解，寻找发电企业和供电公司利益均衡的规划方案，但仅从经济性的角度考虑DG优化配置问题并不全面。文献[9]从线路升级费用、供电可靠性和网损的角度建立了DG多目标规划模型，采用线性权重法将多目标转化为单目标处理，虽然降低了求解难度，但由于各指标的数量级相差较大，不同权重系数对优化结果的影响并不明显，不能真实反映决策者对各指标的侧重程度。文献[10]采用果蝇优化算法(fruit fly optimization algorithm，FOA)对配电网中变电站规划模型进行求解，但算法在求解过程中易出现收敛精度低、寻优速度慢和早熟收敛等问题。

目前关于果蝇优化算法的改进研究仍处于起步阶段，并且还没有关于将果蝇优化算法应用于求解DG优化配置问题的相关研究。

针对以上问题，从DG投资效益、电压指标和网损的角度出发，采用模糊隶属度处理技术，建立配电网多目标模糊规划模型。将细菌趋化思想中的吸引和排斥操作引入果蝇优化算法，提出一种改进的果蝇优化算法(improved fruit fly optimization algorithm，IFOA)，并首次将其应用于求解DG优化配置问题。算例仿真结果表明，与粒子群优化算法(particle swarm optimization，PSO)和果蝇优化算法相比，改进的果蝇优化算法在求解精度和寻优速度上优势明显。

1 含DG的多目标模糊规划数学模型

1.1 目标函数

1.1.1 DG投资效益

单位DG投资所获得的年收益为[8]

(1)

式中：CTPF为DG并网后折算到每年的收益，包括DG的卖电收益和国家政策补贴；CINV为DG投资折算到每年的投资成本，包括占地费用、安装费用和运行维护费用等。

(2)

(3)

1.1.2 电压指标

电压指标包括支路电压稳定性指标和节点电压偏移指标。支路电压稳定性指标为所有支路电压稳定指数之和，描述的是所有支路的电压稳定性[11]。电压偏移指标为所有节点电压与基准电压差之和，反映的是整体节点电压的偏移程度。这2个指标能充分衡量配电网电压质量。

(4)

(5)式中：UVSI为支路电压稳定性指标；UVDI为电压偏移指标；N为网络节点数；T为网络负荷节点数；Pj、Qj分别为节点j的有功负荷和无功负荷；Rij、Xij分别为ij支路的电阻和电抗；Ui为节点i的电压幅值；Urate为基准电压值。

综合考虑节点电压偏移和支路电压稳定性的电压评价指标为[12]

U=α1UVSI+α2UVDI

(6)

式中：α1和α2分别为UVSI和UVDI的权重系数，取值均为0.5。

1.1.3 网损

网损是评价配电网经济运行的重要指标，DG的合理优化配置能有效降低网损，网损表达式为

(7)

式中：Yij为ij支路的导纳；θij为支路ij的阻抗角；δij为节点i、j的电压相角差。

1.2 隶属度函数

考虑不同目标函数间的数量级不同，为避免过度优化某一指标，采用线性函数表示各子目标的隶属度函数，将其加权求和作为最终优化目标函数。

(8)

(9)

(10)

式中：λ1、λ2、λ3分别为DG投资效益、电压指标和网损的隶属度；Cpsc,max、Cpsc,min分别为单独优化DG投资效益时的最大值与最小值；Umax、Umin分别为单独优化电压指标时的最大值与最小值；Ploss,max、Ploss,min分别为单独优化网损时的最大值与最小值。

由上述分析，采用模糊隶属度技术将多目标规划问题转化为单目标规划问题处理，具体为

maxF=aλ1+bλ2+cλ3

(11)

式中：F为综合隶属度，其值越大表示规划方案越优；a、b、c分别为λ1、λ2、λ3的权重系数，取值均为1/3。

1.3 约束条件

DG多目标优化配置的等式约束条件和不等式约束条件为

(12)

式中：PDGi和QDGi分别为节点i处DG注入的有功功率和无功功率；Gij和Bij分别为ij支路的电导和电纳；ei和fi分别为节点i电压的实部和虚部；Ui,max、Ui,min分别为节点i电压允许的最大值和最小值；δ为DG渗透率极限系数；NDG为DG安装节点集合；SDGi和SDGi,max分别为节点i处DG安装容量及其最大值；Iij和Iij,max分别为支路ij的电流和允许电流的最大值。

2 DG多目标配置求解算法

2.1 果蝇优化算法

果蝇优化算法[13]是通过效仿果蝇觅食行为而提出一种新颖的仿生智能算法。果蝇具有灵敏的感知器官，尤其是嗅觉和视觉。果蝇在觅食过程中，首先通过嗅觉搜集漂浮在空气中的食物气味，可探知数十公里外的食物源，然后向该区域飞行，再通过视觉寻找食物和伙伴聚集的位置进而确定最终的食物位置。

根据果蝇搜索食物的特征，果蝇优化算法的实现步骤可以归纳为：

(1)设置种群规模Mpop和最大迭代次数nmax，在可行域范围内随机初始化群体位置Xaxis和Yaxis。

(2)计算果蝇个体搜索的随机方向和距离。

(13)

式中：Xi、Yi为果蝇i的位置；Drandvalue为随机搜索距离。

(3)由于食物位置为待求量，首先估计果蝇个体与原点的距离Dist,i，然后计算个体的气味浓度判定值ci。

(14)

(4)将每一个体气味浓度判定值代入气味浓度函数(或称目标函数)，计算得到当前个体的气味浓度值csmell。

csmell,i=f(ci)

(15)

(5)对果蝇个体气味浓度值排序，找到气味浓度最佳的个体(适用于求解极小值问题)。

[csmell,best,cindex,best]=min(csmell,i)

(16)

式中：csmell,best为当代最佳味道浓度值；cindex,best为当代最优个体位置索引。

(6)记录并保存最佳气味浓度值和群体位置。

(17)

式中：csmell,history为历史最佳味道浓度值。

(7)进入迭代寻优，重复进行步骤(1)—(5)，并判断当前迭代次数是否小于最大迭代次数且每次迭代最佳气味浓度值是否优于上次最佳味道浓度值，若是，进行步骤(6)。

2.2 改进果蝇优化算法

果蝇优化算法在寻优过程中仅追踪当代最优个体实现群体位置的更新，即一旦发现最优个体位置，所有果蝇都将向该位置飞行。这种搜索方式不仅使种群过于拥挤，降低了种群多样性，同时也缩小了可行域的搜索空间，并且若该个体并非全局最优时，很容易使算法陷入局部最优，早熟收敛。针对这一问题，本文效仿细菌在觅食过程中的趋化思想[14]，将排斥(远离驱除剂)和吸引(靠近引诱剂)操作引入果蝇优化算法寻优过程中，根据气味浓度值的方差判断果蝇是执行排斥操作，还是执行吸引操作，动态调整群体位置更新策略，以提高种群多样性，降低算法陷入局部最优的可能。

改进果蝇优化算法的求解步骤如下：

(1)设置种群规模Mpop和最大迭代次数nmax，在可行域范围内随机初始化群体位置Xaxis和Yaxis。

(2)按公式(13)对果蝇位置初始化，按公式(14)—(15)计算果蝇个体的气味浓度值判定值及气味浓度值。

(3)按式(18)记录并保存最佳和最差味道浓度值和其位置。

(18)

式中：Xb、Yb分别为当代最优个体位置；csmell,worst、csmell,history分别为当代和历史最差味道浓度值；cindex,worst为当代最差个体位置索引；Xw、Yw为当代最差个体位置。

(4)按式(19)和式(20)计算种群气味浓度平均值csmell,avg及方差σ2。

(19)

(20)

(5)给定方差阀值δ，若σ2≤δ，则执行排斥操作，按式(21)更新群体位置；若σ2>δ，则执行吸引操作，按式(22)更新群体位置。

(21)

(22)

(6)进入迭代寻优，重复执行步骤(2)—(3)，并判断当前迭代次数是否小于最大迭代次数且每次迭代最佳味道浓度值是否优于上次最佳味道浓度值，若是，进行步骤(4)—(6)。

基于细菌趋化思想的果蝇位置更新策略，有效解决了传统FOA仅向最优个体靠近所引起的种群多样性降低和早熟收敛的问题。采用改进果蝇优化算法对DG多目标模糊规划模型进行求解，其求解流程如图1所示。

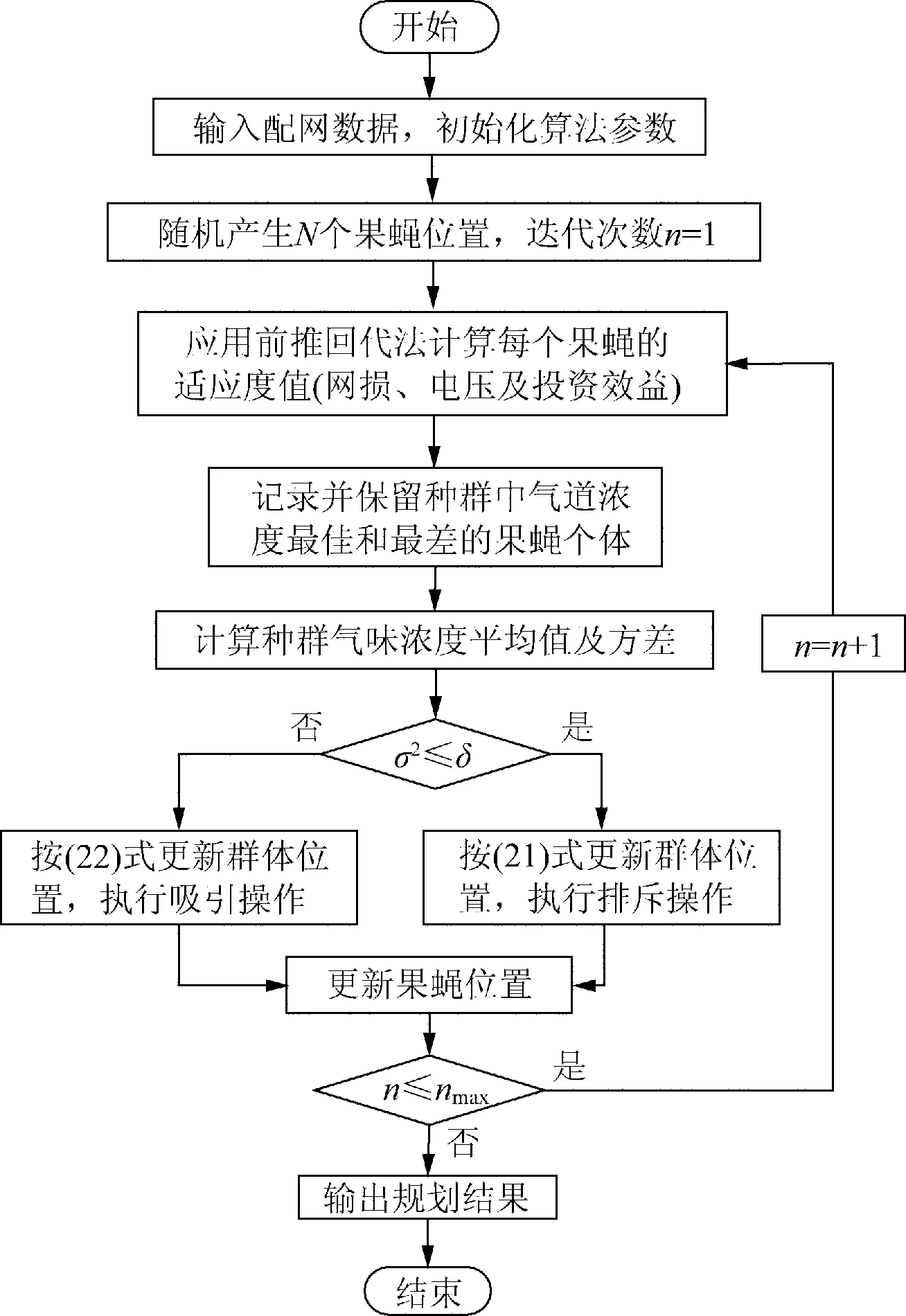
图1 基于IFOA的DG多目标模糊规划求解流程Fig.1 Solution process of DG multi-objective fuzzy programming based on IFOA

3 算例分析

基于Matlab仿真软件平台，采用IEEE 33节点配电网系统作为仿真算例，其中系统总有功负荷为 3 715 kW，总无功负荷为2 300 kvar，基准电压为 12.66 kV，网络拓扑结构如图2所示，系统详细参数见文献[15]。

图2 IEEE 33节点配电网拓扑图Fig.2 Topology of IEEE 33 node distribution network

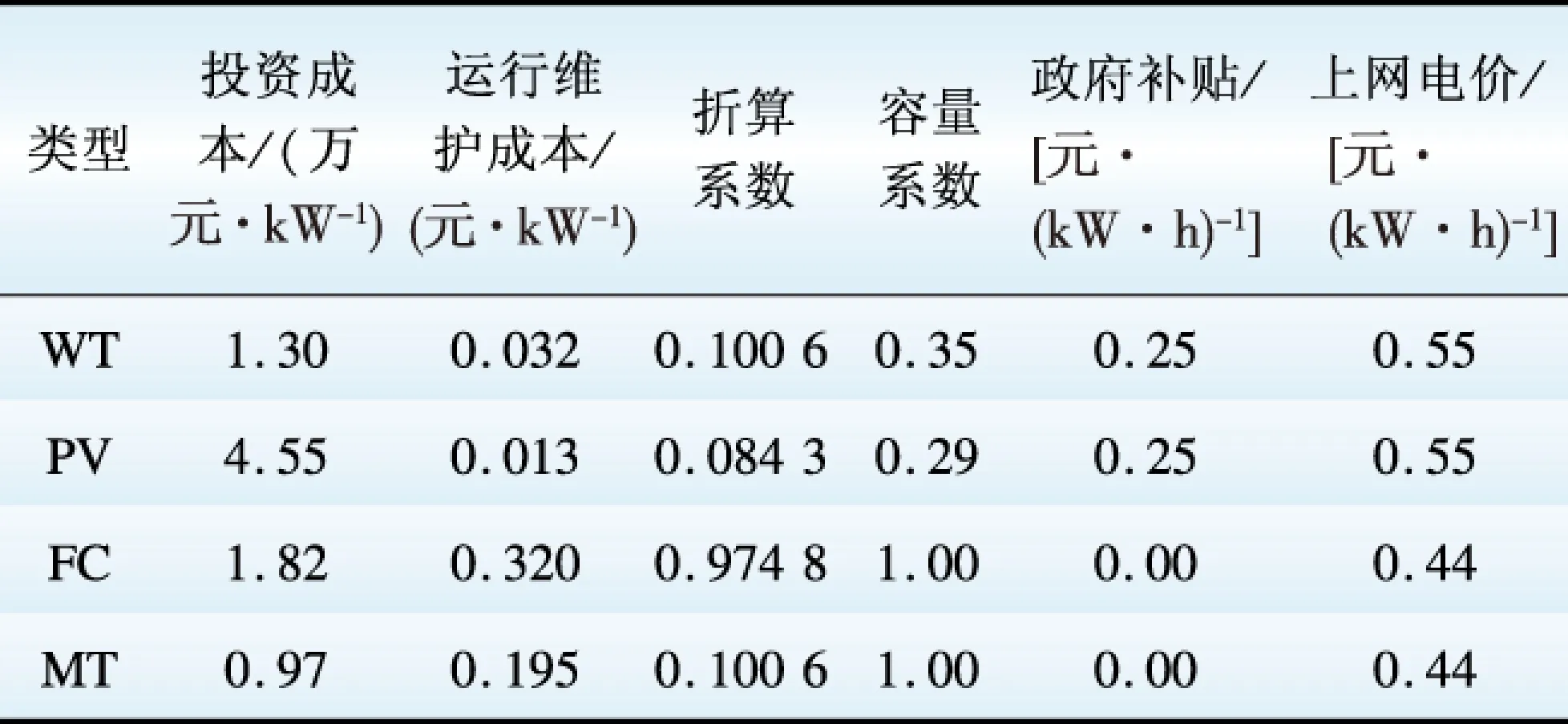
DG类型包括风电(wind turbine，WT)、光伏(photovoltaic，PV)、微型燃料汽轮机(micro-turbine，MT)和燃料电池(fuel cell，FC)，将接入配电网的DG当作负的PQ节点处理，DG投资运行参数详见表1。DG待安装位置分别为：MT待安装位置为13号节点；PV待安装位置为18号节点；FC待安装位置为21号节点；WT待安装位置为33号节点。假定4种类型DG的功率因数恒定均为0.9，DG总出力不超过系统负荷的30%，单位安装容量均为10 kW。算法参数设置：果蝇种群规模为Mpop=40；最大迭代次数为nmax=200；方差阀值δ=0.000 1；果蝇群体位置随机初始化区间为[0，100]；果蝇个体随机搜索方向和距离为[-10，10]。

表1 DG投资运行参数

Table 1 Investment operation parameters of DG

为验证IFOA在求解此类问题的有效性，分别采用IFOA、FOA和PSO进行优化计算。其中FOA参数设置与本文一致，PSO参数设置见文献[16]。图3为3种智能算法的收敛曲线。由图3可知，IFOA和PSO收敛速度相同，均在迭代60次左右收敛，但其求解精度却远不如IFOA；FOA收敛速度最差，在迭代150次左右才收敛，其求解精度优于PSO，但不如IFOA。综上分析可知，IFOA在收敛速度和求解精度方面都优于FOA和PSO，同时也说明了采用IFOA进行DG优化配置计算的可行性。

表2为不同优化方法求解得到的DG最优配置情况。从表2数据可知，3种智能算法中IFOA的降损效果和电压指标最好，分别较未优化前降低了57.5%和41.6%，但其投资效益却是最差的。结合图3分析可知，虽然IFOA优化计算得到的3个子目标并非都是最优，但其综合隶属度明显优于其余2种算法。同时可得，配电网的电压质量和网损的改善是以损害DG投资效益为代价的，即3个子目标存在竞争关系。因此，在对DG进行优化配置时，应综合衡量各指标的重要程度。本文建立的多目标模糊规划模型，能合理协调各子目标间的关系，更加直观地反映各规划方案的优劣。

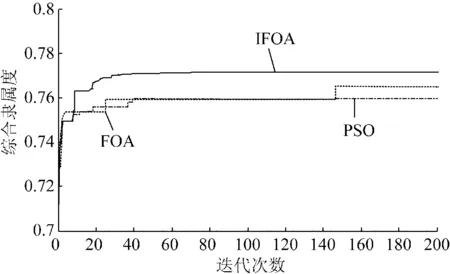
图3 不同优化方法的收敛曲线Fig.3 Convergence curve of different optimization methods

表2 不同优化方法的DG优化配置情况

Table 2 Optimal allocation of DG with different methods

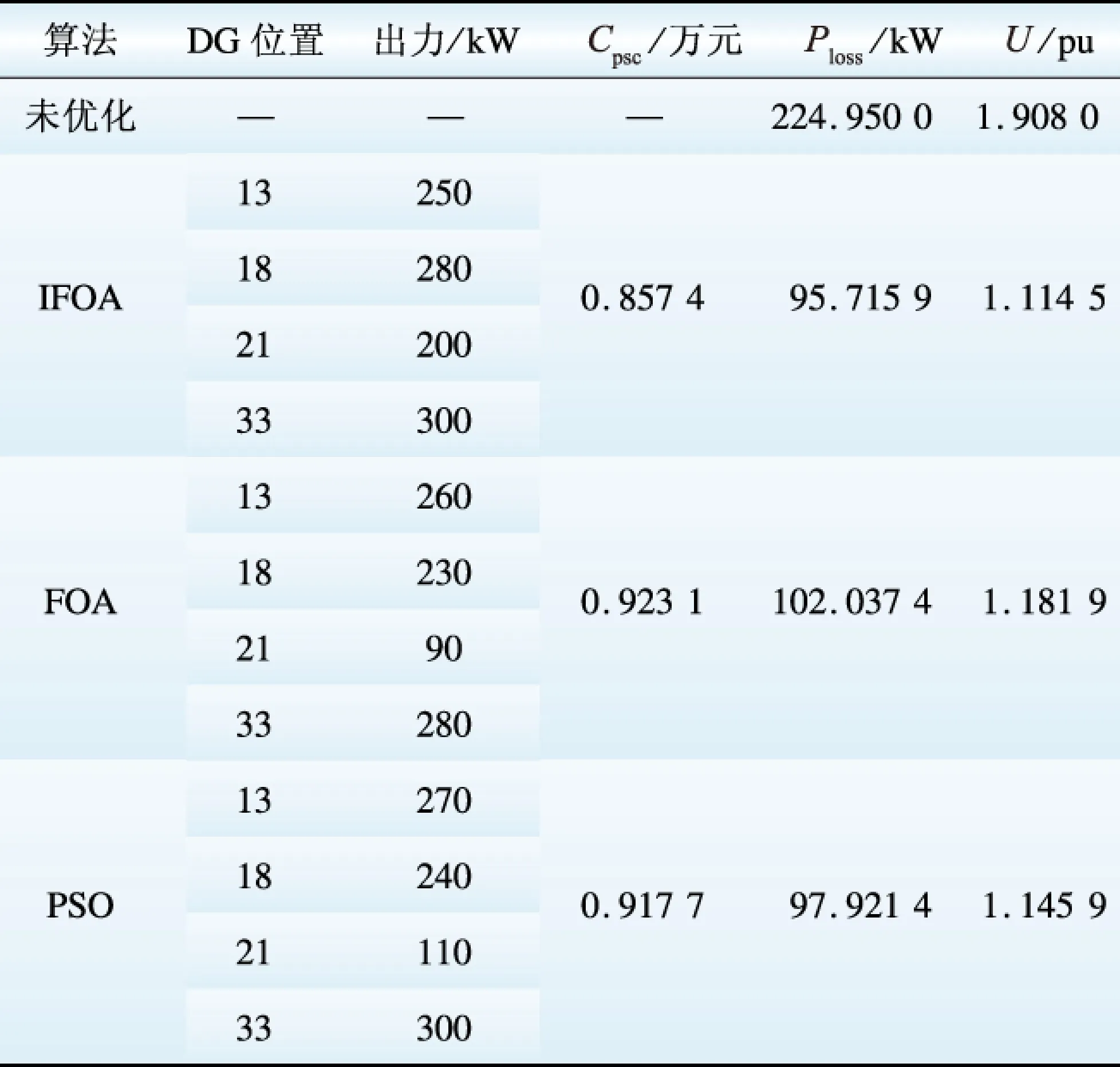
图4为不同优化算法得到的电压曲线。从图4可知，采用IFOA、FOA和PSO 3种算法进行DG优化后的电压曲线都得到了显著改善，其中采用IFOA优化的电压曲线最为理想。未优化前系统最低电压为0.903 8 pu，平均电压为0.945 4 pu。而经IFOA优化得到的最低电压为0.936 0 pu，平均电压为0.971 8 pu，最低电压和平均电压较优化前分别提高了0.032 2 pu和0.026 4 pu。综上分析可知，DG合理优化配置不仅能有效降低网损，也能改善电压质量，提高配电网供电可靠性。

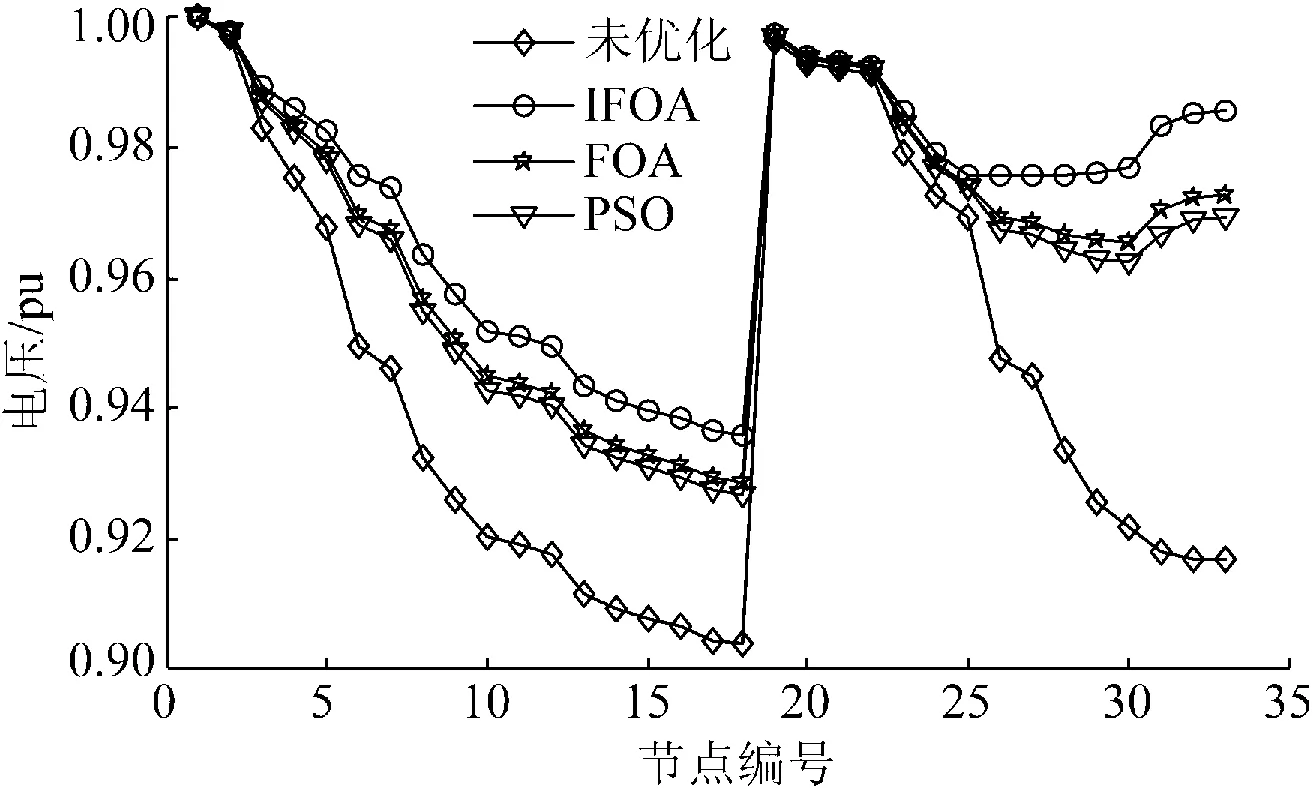
图4 不同优化方法的电压曲线Fig.4 Voltage curve of different optimization methods

4 结论

(1)从经济效益、网损和电压质量等多角度评价DG优化配置的可行性，使得到的规划方案更具说服力。应用模糊技术建模，克服了由于各子目标数量级不同所带来的过度优化问题，方便决策者更加直观地评价各规划方案的优劣。

(2)改进的果蝇优化算法将吸引和排斥操作引入算法寻优过程中，根据当前环境信息动态调整群体位置更新策略，提高了种群多样性，有效降低了算法陷入局部最优的可能性。

[1]丁明，石雪梅. 新能源接入主动配电网的影响[J].电力建设，2015，36(1)：76-84. DING Ming, SHI Xuemei. Effective of new energy paralleling to the active distribution networks [J]. Electric Power Construction, 2015, 36(1): 76-84.

[2]刘健，张志华，黄炜，等.分布式电源接入对配电网故障及电压质量的影响分析[J].电力建设，2015，36(1)：115-121. LIU Jian, ZHANG Zhihua, HUANG Wei, et al. Influence of distributed generation on fault location and voltage quality of distribution network[J]. Electric Power Construction, 2015, 36(1): 115-121.

[3]陈海东，庄平，夏建矿，等.基于改进萤火虫算法的分布式电源优化配置[J].电力系统保护与控制，2016，44(1): 149-154. CHEN Haidong, ZHUANG Ping, XIA Jiankuang, et al. Optimal power flow of distribution network with distributed generation based on modified firefly algorithm [J]. Power System Protection and Control, 2016, 44(1): 149-154.

[4]芦晶晶，赵渊，赵勇帅，等.含分布式电源配电网可靠性评估的点估计法[J].电网技术，2013，37(8)：2250-2257. LU Jingjing, ZHAO Yuan, ZHAO Yongshuai, et al. A pointestimation method for reliability evaluation of distribution network with distributed generation [J]. Power System Technology, 2013, 37(8): 2250-2257.

[5]孙建龙，吴锁平，陈燕超.基于改进NSGA2算法的配电网分布式电源优化配置[J].电力建设，2014，35(2)：86-90. SUN Jianlong, WU Suoping, CHEN Yanchao. Optimal configuration of distributed generation in distribution network based on improved NSGA2[J]. Electric Power Construction, 2014, 35(2): 86-90.

[6]GOLSHAN M E H, AREFIFAR S A. Distributed generation, reactive sources and network-configuration planning for power and energy-loss reduction[J]. IEE Proceedings-Generation, Transmission and Distribution, 2006, 153(2): 127-136.

[7]朱勇，杨京燕，张冬清.基于有功网损最优的分布式电源规划[J].电力系统保护与控制，2011，39(21)：12-16. ZHU Yong, YANG Jingyan, ZHANG Dongqing. Planning of distributed generation based on optimal real power losses [J]. Power System Protection and Control, 2011, 39(21): 12-16.

[8]张立梅，唐巍，王少林，等.综合考虑配电公司及独立发电商利益的分布式电源规划[J].电力系统自动化，2011，35(4)：23-28. ZHANG Limei, TANG Wei, WANG Shaolin, el al. Distributed generators planning considering benefits for distribution power company and independent power suppliers [J]. Automation of Electric Power Systems, 2011, 35(4): 23-28.

[9]SHAABAN M F, ATWA Y M, EI-SAADANY E F. DG allocation for benefit maximization in distribution networks [J]. IEEE Transactions on Power Systems, 2013, 28(2): 639-649.

[10]彭文，杜晓东，石敏.基于负荷区域划分的配电变电站规划模型[J].电力自动化设备，2015，35(1)：112-117. PENG Wen, DU Xiaodong, SHI Min. Distribution substation planning model based on load region division [J]. Electric Power Automation Equipment, 2015, 35(1): 112-117.

[11]CHAKRAVOTRY M，DAS D. Voltage stability analysis of radial distribution networks [J]. International Journal of Electrical Power & Energy Systems, 2001, 23(2): 129:135.

[12]栗然，马慧卓，祝晋尧，等.分布式电源接入配电网多目标优化规划[J].电力自动化设备，2014，34(1)：6-13. LI Ran, MA Huizhuo, ZHU Jinrao, et al. Multi-objective optimization for DG integration into distribution system[J]. Electric Power Automation Equipment, 2014, 34(1): 6-13.

[13]PAN W T. A new fruit fly optimization algorithm: taking the financial distress model as an example [J]. Knowledge-Based Systems, 2012, 26: 69-74.

[14]CHO J H, PARK J I, JEONG J S, et al. Bacterial foraging with quorum sensing based optimization algorithm[C] //Fuzzy Systems, 2009. FUZZ-IEEE 2009. IEEE International Conference on. IEEE, 2009: 29-34.

[15]AMAN M M, JASMON G B, BAKAR A H A, et al. A new approach for optimum simultaneous multi-DG distributed generation Units placement and sizing based on maximization of system loadability using HPSO (hybrid particle swarm optimization) algorithm [J]. Energy, 2014, 66: 202-215.

[16]吴凯，周西峰，郭前岗.基于粒子群神经网络的负荷预测方法研究[J].电测与仪表，2013，50(3)：29-32. WU Kai, ZHOU Xifeng, GUO Qiangang. Study of load forecasting method based on particle swarm optimization neural network[J]. Electrical Measurement & Instrumentation, 2013, 50(3): 29-32.

(编辑景贺峰)

Optimal Configuration of Distributed Generation Based on Improved Fruit Fly Optimization Algorithm

GUAN Tiansheng1, WANG Qi2, LIU He3,ZHENG Yuan4, LI Dexin3, LIU Yadong3, PAN Chao5

(1.Training Centre of State Grid Jilinsheng Electric Power Supply Company, Changchun 130062, China;2. China Power Engineering Consulting Group Northeast Electric Power Design Institute Co., Ltd., Changchun 130021, China; 3. Electric Power Research Institute, State Grid Jilinsheng Electric Power Supply Company,Changchun 130021, China; 4. Jilin Engineering Vocational College, Siping 136001, Jinlin Province, China;5. School of Electrical Engineering, Northeast Dianli University, Jilin 132012, Jilin Province, China)

This paper researches the optimal allocation problem of distributed generation (DG) in distribution network, and establishes a multi-objective optimal configuration considering investment benefit, voltage quality and power loss comprehensively based on fuzzy membership technique, which can effectively solve the excessive optimization problem caused by different magnitude of targets. We improve a new bionic intelligent algorithm-fruit fly optimization algorithm (FOA) and introduce the operation of attraction and repulsion into the algorithm optimization process by following the chemotaxis of bacteria in foraging process to improve the population diversity and reduce the possibility of falling into local optimum. The simulation results of IEEE 33 node system show that, compared with the traditional FOA and particle swarm optimization (PSO) algorithm, the improved fruit fly optimization algorithm (IFOA) has a great advantage in search speed and accuracy and can quickly and effectively search the optimal configuration, which verify the validity and rationality of the improved algorithm.

improved fruit fly optimization algorithm (IFOA); distribution network; distributed generation (DG); multi-objective optimization; comprehensive membership degree

TM 72

1000-7229(2016)06-0103-06

10.3969/j.issn.1000-7229.2016.06.015

2016-03-01

关添升(1984)，女，硕士，工程师，主要研究方向为智能变电站技术和分布式电源规划；

王琦(1983)，男，硕士，工程师，主要研究方向为新能源并网和电力工程造价；

刘赫(1984)，男，博士，工程师，主要研究方向为智能电网设备故障检测与诊断技术及分布式电源规划；

郑媛(1988)，女，本科，助理工程师，主要研究方向为计及新能源随机性的优化调度以及新能源并网；

李德鑫(1985)，男，硕士，工程师，主要研究方向为新能源并网；

刘亚东(1983)，男，硕士，工程师，主要研究方向为配电网规划与运行；

潘超(1981)，男，博士，副教授，主要研究方向为配电网规划与运行。